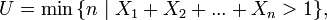e (constante math??matique)
Saviez-vous ...
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. Parrainage d'enfants aide les enfants du monde en d??veloppement ?? apprendre aussi.
Le math??matique constante e est l'unique de nombre r??el tel que la valeur de la d??riv??e (pente de la tangente en ligne) de la fonction f (x) = x e au point x = 0 est exactement 1. La fonction e x ainsi d??finies est appel?? la fonction exponentielle , et son inverse est le logarithme naturel , ou logarithme e base. Le nombre e est aussi commun??ment d??fini comme la base du logarithme naturel (en utilisant une int??grale de d??finir celui-ci), tel que le limite d'une certaine s??quence , ou comme la somme d'un certain s??rie (voir repr??sentations de e , ci-dessous).
Le nombre e est l'un des num??ros les plus importantes en math??matiques, aux c??t??s de l'additif et identit??s multiplicatifs 0 et 1 , la constante π et l' unit?? imaginaire i.
Le nombre e est parfois appel?? le num??ro d'Euler apr??s la Swiss math??maticien Leonhard Euler , ou Napier constante en l'honneur de l' ??cossais math??maticien John Napier qui a introduit logarithmes . (E ne doit pas ??tre confondue avec γ - la Euler-Mascheroni constant, parfois appel?? tout simplement la constante d'Euler.)
Comme e est transcendantale, et donc irrationnelle , sa valeur ne peut ??tre donn??e exactement comme un nombre d??cimal fini ou ??ventuellement r??p??ter. La valeur num??rique de e tronqu?? ?? 20 d??cimales est:
- 2,71828 18284 59045 23536 ...
Histoire
Les premi??res r??f??rences ?? la constante ont ??t?? publi??s en 1618 dans le tableau d'une annexe d'un ouvrage sur les logarithmes par John Napier. Cependant, ce ne contenait pas la constante elle-m??me, mais simplement une liste des logarithmes naturels calcul??es ?? partir de la constante. On suppose que la table a ??t?? ??crit par William Oughtred. La ??d??couverte?? de la constante elle-m??me est cr??dit?? Jacob Bernoulli, qui a tent?? de trouver la valeur de l'expression suivante (qui est en fait e):
La premi??re utilisation connue de la constante, repr??sent??e par la lettre b, ??tait en correspondance de Gottfried Leibniz ?? Christiaan Huygens en 1690 et 1691. Leonhard Euler a commenc?? ?? utiliser la lettre e pour la constante en 1727, et la premi??re utilisation de l'e dans une publication ??tait Mechanica d'Euler (1736). Alors que dans les ann??es suivantes certains chercheurs ont utilis?? la lettre c, e ??tait plus commun et a fini par devenir la norme.
Les raisons exactes de l'utilisation de la lettre e ne sont pas connus, mais il peut ??tre parce que ce est la premi??re lettre du mot exponentielle. Une autre possibilit?? est que Euler utilis?? parce que ce ??tait la premi??re voyelle apr??s une, qu'il utilisait d??j?? pour un autre num??ro, mais sa raison d'utiliser voyelles est inconnue. Il est peu probable que Euler choisi la lettre parce que ce est la premi??re lettre de son nom de famille, car il ??tait un homme tr??s modeste et a essay?? de donner le cr??dit appropri?? pour le travail des autres.
Applications
Le probl??me d'int??r??t compos??
Jacob Bernoulli a d??couvert cette constante en ??tudiant une question sur int??r??ts compos??s.
Un exemple simple est un compte qui commence par $ 1,00 et paie un int??r??t de 100% par an. Si l'int??r??t est cr??dit?? une fois, ?? la fin de l'ann??e, la valeur est de 2,00 $; mais si l'int??r??t est calcul?? et ajout?? deux fois dans l'ann??e, le $ 1 est multipli?? par 1,5 ?? deux reprises, ce qui donne $ 1,00 ?? 1,5?? = $ 2,25. Aggravant donne trimestrielle $ 1,00 ?? 1,25 = 4 2.4414 $ ..., et la pr??paration des rendements mensuels $ 1,00 ?? (1,0833 ...) = 12 $ 2,613035 ....
Bernoulli remarqu?? que cette s??quence se approche d'une limite de plus en plus petits intervalles de composition. Aggravant rendements hebdomadaires 2.692597 $ ..., tout en aggravant quotidienne donne 2.714567 $ ..., ?? seulement deux cents de plus. En utilisant n comme le nombre d'intervalles de composition, avec int??r??t 1/ n dans chaque intervalle, la limite pour n grand est le nombre qui est venu ?? ??tre connu comme e; avec m??lange continu, la valeur du compte atteindra 2.7182818 $ .... Plus g??n??ralement, un compte qui commence ?? $ 1, et les rendements (1+ R) dollars ?? l'int??r??t simple, donneront dollars de R e avec m??lange continu.
Essais de Bernoulli
Le nombre e lui-m??me a ??galement des applications ?? la th??orie des probabilit??s , o?? il se pose d'une mani??re ??videmment pas li??e ?? la croissance exponentielle. Supposons qu'un joueur joue une machine ?? sous qui paie avec une probabilit?? de un ?? n et joue n fois. Alors, pour n grand (comme un millions) de la probabilit?? que le joueur va gagner rien du tout, ce est (environ) 1/ e.
Ceci est un exemple d'un Bernoulli processus des essais. Chaque fois que le joueur joue les fentes, il ya un un sur un million de chances de gagner. Jouer un million de fois est mod??lis?? par la loi binomiale , qui est ??troitement li??e ?? la bin??me. La probabilit?? de gagner k fois sur un million d'essais ce est;
En particulier, la probabilit?? de gagner z??ro fois (k = 0) est
Ce est tr??s proche de la limite suivante pour 1/ e:
D??rangements
Une autre application de e, ??galement d??couvert en partie par Jacob Bernoulli avec Pierre R??mond de Montmort est dans le probl??me de la d??rangements, aussi connu comme le probl??me de contr??le de chapeau. Ici n clients sont invit??s ?? une f??te, et ?? la porte chaque client v??rifie son chapeau avec le ma??tre d'h??tel qui les place ensuite dans des bo??tes ??tiquet??es. Mais le majordome ne conna??t pas le nom des clients, et doit donc les mettre dans des bo??tes choisis au hasard. Le probl??me de de Montmort est: quelle est la probabilit?? qu'aucun des chapeaux se mettre dans la case de droite. La r??ponse est:
Comme le nombre de visiteurs n tend vers l'infini, p n e 1/ approches. En outre, le nombre des moyens les chapeaux peuvent ??tre plac??s dans les bo??tes de sorte qu'aucun des chapeaux est dans la case de droite est exactement n! / E, arrondi ?? l'entier le plus proche.
Asymptotique
Le nombre e se produit naturellement dans le cadre de nombreux probl??mes impliquant asymptotique. Un exemple bien connu est La formule de Stirling pour l'asymptotique de la fonction factorielle , dans lequel ?? la fois le nombre e et π ENTR??E:
Une cons??quence particuli??re de ce est
e dans le calcul

La principale motivation pour introduire le nombre e, en particulier dans le calcul , est d'effectuer diff??rentiel et calcul int??gral avec les fonctions exponentielles et logarithmes . Une fonction exponentielle g??n??rale y = a x a d??riv?? donn?? comme limite :
La limite sur le c??t?? droit est ind??pendant de la variable x: il ne d??pend que de la base a. Lorsque la base est e, cette limite est ??gale ?? un, et si e est symboliquement d??finie par l'??quation:
Par cons??quent, la fonction exponentielle avec la base e est particuli??rement adapt?? ?? faire le calcul. Le choix de e, par opposition ?? un autre nombre, comme la base de la fonction exponentielle effectue des calculs impliquant le d??riv?? beaucoup plus simples.
Une autre motivation vient d'examiner la base-un logarithme . Compte tenu de la d??finition de la d??riv??e de connecter un x la limite:
Une fois de plus, il ya une limite ind??termin??e qui ne d??pend que de la base d'un, et si cette base est e, la limite est une. Donc, symboliquement,
Le logarithme dans cette base sp??ciale est appel?? le logarithme naturel (souvent repr??sent??e comme "ln"), et il se comporte aussi bien sous la diff??renciation car il n'y a pas de limite ind??termin??e pour mener ?? bien les calculs.
Il ya donc deux fa??ons de s??lectionner un num??ro sp??cial a = e. Une fa??on est de d??finir la d??riv??e de la fonction exponentielle un x ?? un x. L'autre fa??on est de mettre la d??riv??e de la base d'un logarithme en 1 / x. Dans chaque cas, on arrive ?? un choix pratique de base pour faire le calcul. En fait, ces deux bases sont en fait la m??me, le nombre e.
Caract??risations alternatives
Autres caract??risations de e sont ??galement possibles: l'une est que le limite d'une suite, un autre est tel que la somme d'une s??rie infinie, et d'autres encore se appuient sur le calcul int??gral . Jusqu'?? pr??sent, les deux (??quivalentes) propri??t??s suivantes ont ??t?? introduites:
1. Le nombre e est l'unique positif nombre r??el de telle sorte que
2. Le nombre e est le nombre r??el positif unique tel que
Les trois caract??risations suivantes peuvent ??tre ??quivalente ??prouv??e:
3. Le nombre e est la limite

4. Le nombre e est la somme de la s??rie infinie
o?? n! est la factorielle de n.
5. Le nombre e est le nombre r??el positif unique tel que
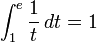 .
.
Propri??t??s
Calcul
Comme dans la motivation, la fonction exponentielle f (x) = x e est important en partie parce que ce est la fonction non triviale unique (?? multiplication par une constante) qui est son propre d??riv??
et donc sa propre primitive ainsi:
Fonctions exponentielle comme
Le nombre x = e est o?? le maximum global se produit pour la fonction:
Plus g??n??ralement, ![x = \! \ \ sqrt [n] {e}](../../images/105/10516.png) est o?? le maximum global se produit pour la fonction
est o?? le maximum global se produit pour la fonction
L'infini t??tration
converge seulement si 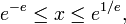 due ?? un th??or??me de Leonhard Euler .
due ?? un th??or??me de Leonhard Euler .
Enfin, la fonction exponentielle e x est g??n??ralement d??finie comme
La th??orie des nombres
Le nombre r??el e est irrationnel (voir preuve que e est irrationnel), et en outre est transcendantale ( Th??or??me Lindemann-Weierstrass). Ce ??tait le premier num??ro ?? prouver transcendantale sans avoir ??t?? construit sp??cialement ?? cet effet (comparer avec Nombre de Liouville). La preuve a ??t?? donn??e par Charles Hermite en 1873. Il est suppos?? ??tre normal.
Les nombres complexes
Il dispose en La formule d'Euler, une formule important li?? ?? des nombres complexes :
Le cas particulier avec x = π est connu comme l'identit?? d'Euler :
d'o?? il r??sulte que, dans le branche principale du logarithme,
En outre, en utilisant les lois pour exponentiation,
qui est la formule de de Moivre.
Repr??sentations de e
Le nombre n peut ??tre repr??sent?? comme un nombre r??el dans une vari??t?? de fa??ons: en tant que s??rie infinie, une produit infini, un fraction continue, ou d'un limite d'une suite. Le chef parmi ces repr??sentations, en particulier dans introductifs calcul des cours est la limite
donn??e ci-dessus, ainsi que la s??rie
donn??e par l'??valuation de la s??rie de puissance ci-dessus pour e x ?? x = 1.
D'autres repr??sentations moins courantes sont ??galement disponibles. Par exemple, e peut ??tre repr??sent?? comme un infini simples fraction continue:
Ou, dans une forme plus compacte (s??quence A003417 dans OEIS ):
Qui peut ??tre ??crit plus harmonieusement en permettant z??ro:
Beaucoup d'autres s??ries, la s??quence, fraction continue, et les repr??sentations infinies de produits de e ont ??galement ??t?? d??velopp??s.
Repr??sentations stochastiques de e
En plus des expressions analytiques pour d??terministes repr??sentation de E, comme d??crit ci-dessus, il existe des protocoles stochastiques pour l'estimation de e. Dans un tel protocole, des ??chantillons al??atoires 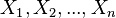 de taille n de la r??partition uniforme sur (0, 1) sont utilis??es pour approximer e. Si
de taille n de la r??partition uniforme sur (0, 1) sont utilis??es pour approximer e. Si
puis l'attente de U est e: 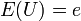 . Ainsi moyennes de l'??chantillon de variables U se rapprocheront e.
. Ainsi moyennes de l'??chantillon de variables U se rapprocheront e.
Chiffres connus
Le nombre de chiffres connus de e a augment?? de fa??on spectaculaire au cours des derni??res d??cennies. Cela est d?? ?? la fois ?? l'augmentation de performances des ordinateurs ainsi que des am??liorations algorithmiques.
| Date | Les chiffres d??cimaux | Le calcul effectu?? par |
|---|---|---|
| 1748 | 18 | Leonhard Euler |
| 1853 | 137 | William Shanks |
| 1871 | 205 | William Shanks |
| 1884 | 346 | JM Boorman |
| 1946 | 808 | ? |
| 1949 | 2010 | John von Neumann (sur la ENIAC) |
| 1961 | 100265 | Daniel Shanks & John W. Cl?? |
| 1994 | 10000000 | Robert Nemiroff & Jerry Bonnell |
| Mai 1997 | 18199978 | Patrick Demichel |
| Ao??t 1997 | 20000000 | Birger Seifert |
| Septembre 1997 | 50000817 | Patrick Demichel |
| F??vrier 1999 | 200000579 | Sebastian Wedeniwski |
| Octobre 1999 | 869894101 | Sebastian Wedeniwski |
| 21 novembre 1999 | 1250000000 | Xavier Gourdon |
| 10 juillet 2000 | 2147483648 | Shigeru Kondo & Xavier Gourdon |
| 16 juillet 2000 | 3221225472 | Colin Martin & Xavier Gourdon |
| 2 ao??t 2000 | 6442450944 | Shigeru Kondo & Xavier Gourdon |
| 16 ao??t 2000 | 12884901000 | Shigeru Kondo & Xavier Gourdon |
| 21 ao??t 2003 | 25100000000 | Shigeru Kondo & Xavier Gourdon |
| 18 septembre 2003 | 50100000000 | Shigeru Kondo & Xavier Gourdon |
| 27 avril 2007 | 100000000000 | Shigeru Kondo & Steve Pagliarulo |
e dans la culture de l'ordinateur
Dans contemporaine la culture Internet, les individus et les organisations paient fr??quemment hommage au nombre e.
Par exemple, dans le IPO d??p??t de Google , en 2004, plut??t que d'une quantit?? typique ronde nombre de l'argent, la soci??t?? a annonc?? son intention de lever $ 2,718,281,828, qui est e-milliard de dollars au dollar pr??s. Google a ??galement ??t?? responsable d'un panneau myst??rieuse qui apparaissait dans le coeur de Silicon Valley, et plus tard dans Cambridge, Massachusetts; Seattle, Washington ; et Austin, Texas. Il lu {premier premier 10 chiffres qui se trouve ?? deux chiffres cons??cutifs de e} .com. R??soudre ce probl??me et en visitant le site Web annonc?? conduit ?? un probl??me encore plus difficile ?? r??soudre, ce qui entra??ne ?? son tour Google Labs o?? le visiteur est invit?? ?? soumettre un curriculum vitae. Le premier premier ?? 10 chiffres dans l'e est 7427466391, qui commence ?? la 99e chiffres. (Un flux al??atoire de chiffres a une chance de commencer un premier 10 chiffres plus t??t 98,4%.)
Dans un autre cas, l'??minent informaticien Donald Knuth laisser les num??ros de version de son programme METAFONT approche e. Les deux versions sont, 2,7, 2,71, 2,718, et ainsi de suite.
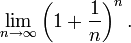
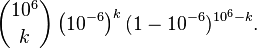
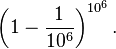
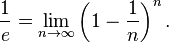

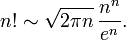
![e = \ lim_ {n \ to \ infty} \ frac {n} {\ sqrt [n] {n!}}.](../../images/104/10492.png)



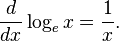
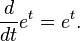
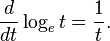
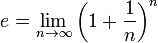
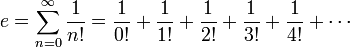




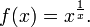
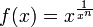
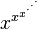
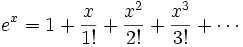
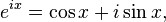
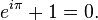
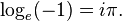

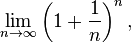
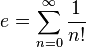
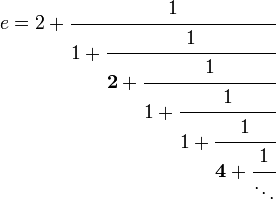
![e = [[2; 1, \ textbf {2}, 1, 1, \ textbf {4}, 1, 1, \ textbf {6}, 1, 1, \ textbf {8}, 1, \ ldots, 1, \ textbf {2n} , 1, \ ldots]] \,](../../images/105/10527.png)
![e = [[1, \ textbf {0}, 1, 1, \ textbf {2}, 1, 1, \ textbf {4}, 1, 1, \ textbf {6}, 1, \ ldots]] \,](../../images/105/10528.png)