
L'??quilibre chimique
Contexte des ??coles Wikip??dia
Cette s??lection de wikipedia a ??t?? choisi par des b??n??voles aidant les enfants SOS de Wikipedia pour cette s??lection Wikipedia pour les ??coles. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
Dans un processus chimique, ??quilibre chimique est l'??tat dans lequel le activit??s chimiques ou les concentrations des r??actifs et des produits ne ont aucun changement net dans le temps. Habituellement, ce serait l'??tat qui r??sulte de l'avant processus chimique proc??de au m??me rythme que leur r??action inverse. Les taux de r??action de la marche avant et arri??re r??actions sont g??n??ralement pas ?? z??ro, mais, ??tant ??gales par ailleurs, il n'y a aucun changement net dans l'un des r??actifs ou de produits concentrations. Ce processus est appel?? ??quilibre dynamique
| |||||
Introduction

Dans une r??action chimique , lorsque les r??actifs sont m??lang??s ensemble dans un r??cipient de r??action (et chauff??e si n??cessaire), l'ensemble des corps r??actionnels ne est pas converti en les produits. Apr??s un certain temps (qui peut ??tre plus courte que millioni??mes de seconde ou plus que l'??ge de l'univers), il viendra un moment o?? un montant fixe de r??actifs existera en harmonie avec une quantit?? fixe de produits, les quantit??s de changement ni plus. Ce est ce qu'on appelle l'??quilibre chimique.
Le concept de l'??quilibre chimique a ??t?? d??velopp?? apr??s Berthollet (1803) a constat?? que certaines r??actions chimiques sont r??versible. Pour toute r??action, tel que
??tre ?? l'??quilibre les taux des r??actions avant et arri??re (arri??re) doivent ??tre ??gaux. Dans ce ??quation chimique avec des fl??ches pointant de harpons dans les deux sens pour indiquer l'??quilibre, A et B sont r??actif esp??ce chimique, S et T sont des esp??ces de produits, et α, β, σ, et τ sont les les coefficients stoechiom??triques des r??actifs et des produits respectifs. La position d'une r??action d'??quilibre est dit de mentir loin vers la droite si, ?? l'??quilibre, presque tous les r??actifs sont utilis??s et loin vers la gauche si gu??re produit est form?? ?? partir des r??actifs.
Guldberg et Waage (1865), se appuyant sur les id??es de Berthollet, a propos?? la la loi d'action de masse:
o?? A, B, S et T sont masses actives et k + et k - sont les constantes de vitesse. Depuis l'avant et vers l'arri??re taux sont ??gaux:
et le rapport des constantes de vitesse est ??galement constante, maintenant connu sous le nom la constante d'??quilibre.
Par convention les produits constituent le num??rateur . Cependant, la la loi d'action de masse ne est valable que pour les r??actions en une ??tape concert??es qui proc??dent par un seul transition Etat et ne est pas valable en g??n??ral, car les ??quations de taux ne, en g??n??ral, suivent pas la stoechiom??trie de la r??action comme Guldberg et Waage a propos?? (voir, par exemple, la substitution nucl??ophile aliphatique par r??action SN1 ou de l'hydrog??ne et du brome pour former le bromure d'hydrog??ne). Egalit?? des taux ?? terme et de r??action en amont, cependant, est un condition n??cessaire ?? l'??quilibre chimique, mais il ne est pas suffisante pour expliquer pourquoi l'??quilibre se produit.
Malgr?? l'??chec de cette d??rivation, la constante d'??quilibre pour la r??action est en effet une constante, ind??pendante des activit??s des diff??rentes esp??ces concern??es, si elle ne d??pend que de la temp??rature observ??e par le Relation de Van't Hoff. L'ajout d'un catalyseur aura une incidence sur la r??action ?? la fois vers l'avant et la r??action inverse de la m??me fa??on et ne aura pas d'effet sur la constante d'??quilibre. Le catalyseur va acc??l??rer deux r??actions augmentant ainsi la vitesse ?? laquelle l'??quilibre est atteint.
Bien que les concentrations ?? l'??quilibre macroscopiques sont constantes dans le temps des r??actions se produisent au niveau mol??culaire. Par exemple, dans le cas de l'acide ??thano??que dissous dans l'eau et formant ??thanoate et ions hydronium,
- CH 3 CO 2 H + H 2 O ⇌ CH 3 CO 2 - + H 3 O +
un proton peut sauter d'une mol??cule d'acide ??thano??que ?? une mol??cule d'eau, puis ?? un ion ??thanoate pour former une autre mol??cule d'acide ??thano??que et en laissant le nombre de mol??cules d'Acide ac??tique inchang??. Ceci est un exemple de ??quilibre dynamique. ??quilibres, comme le reste de la thermodynamique, sont des ph??nom??nes statistiques, moyennes de comportement microscopique.
Le principe de Le Chatelier (1884) est un principe utile qui donne une id??e qualitative de la r??ponse d'un syst??me ?? l'??quilibre ?? des changements dans les conditions de r??action. Si un ??quilibre dynamique est perturb??e par le changement des conditions, la position d'??quilibre se d??place pour contrer le changement. Par exemple, en ajoutant plus S de l'ext??rieur feront appara??tre un exc??dent de produits, et le syst??me va essayer de contrer ce en augmentant la r??action inverse et en poussant le point d'??quilibre vers l'arri??re (si la constante d'??quilibre restera le m??me).
Si l'acide min??ral est ajout?? au m??lange de l'acide ??thano??que, l'augmentation de la concentration de l'ion hydronium, la quantit?? de dissociation doit diminuer ?? mesure que la r??action est entra??n??e vers la gauche conform??ment ?? ce principe. Cela peut aussi ??tre d??duite de l'expression de la constante d'??quilibre pour la r??action:
si {H 3 O +} {augmente CH 3 CO 2 H} {doit augmenter et CH 3 CO 2 -} doit diminuer.
Une version quantitative est donn??e par la quotient de r??action.
JW Gibbs a sugg??r?? en 1873 que l'??quilibre est atteint lorsque le Enthalpie libre du syst??me est ?? sa valeur minimale (en supposant que la r??action est effectu??e sous une pression constante). Ce qui veut dire que la d??riv??e de l'??nergie de Gibbs par rapport ?? r??action de coordonn??es (une mesure de la ampleur de la r??action qui a eu lieu, allant de z??ro pour tous les r??actifs ?? un maximum pour tous les produits) dispara??t, signalant un point fixe. Ce d??riv?? est g??n??ralement appel??, pour certaines raisons techniques, le changement d'??nergie Gibbs. Ce crit??re est ?? la fois n??cessaire et suffisante. Si un m??lange ne est pas ?? l'??quilibre, la lib??ration de l'??nergie d'exc??s de Gibbs (ou Helmholtz ??nergie ?? des r??actions ?? volume constant) est la ??force motrice?? pour la composition du m??lange de changer jusqu'?? ce qu'un ??quilibre soit atteint. La constante d'??quilibre peut ??tre li??e ?? la norme ??nergie de Gibbs changement pour la r??action par l'??quation
o?? R est le constante universelle des gaz et T la temp??rature .
Lorsque les r??actifs sont dissous dans un milieu de haut la force ionique du quotient de les coefficients d'activit?? peuvent ??tre prises pour ??tre constante. Dans ce cas, le quotient de la concentration, K c,
o?? [A] est la concentration de A, etc., est ind??pendante de la concentration des r??actifs d'analyse. Pour cette raison, les constantes d'??quilibre pour les solutions sont habituellement d??termin?? dans les m??dias de grande force ionique. C K varie en fonction de la force ionique, la temp??rature et la pression (ou le volume). De m??me, K p pour les gaz d??pend de pression partielle. Ces constantes sont plus faciles ?? mesurer et rencontr??s dans les cours de chimie du secondaire.
Thermodynamique
La relation entre l'??nergie de Gibbs, et la constante d'??quilibre peut ??tre trouv??e en prenant en compte les potentiels chimiques. La thermodynamique condition d'??quilibre chimique est
- ?? pression constante AG = 0 (AG est le changement ??nergie libre de Gibbs pour la r??action)
- A Aa ?? volume constant = 0 (Aa est le changement de ??nergie libre pour la r??action)
Dans cet article, seul le cas de pression constante est consid??r??e. Le cas de volume constant est important dans g??ochimie et chimie de l'atmosph??re, o?? les variations de pression sont importants. Notez que, si des r??actifs et des produits ??taient en ??tat standard (compl??tement pure), alors il n'y aurait pas de r??versibilit?? et pas d'??quilibre. Le m??lange des produits et r??actifs contribue une grande entropie (connu sous le nom entropie de m??lange) aux Etats contenant m??lange ??gal de produits et r??actifs. La combinaison du changement standard ??nergie de Gibbs et l'??nergie de Gibbs de m??lange d??termine l'??tat d'??quilibre.
En g??n??ral, un syst??me d'??quilibre est d??finie par l'??criture d'une ??quation d'??quilibre de la r??action
Afin de satisfaire ?? la condition thermodynamique pour l'??quilibre, l'??nergie de Gibbs doit ??tre immobile, ce qui signifie que la d??riv??e de G par rapport ?? coordonn??e de r??action (AG) doit ??tre z??ro. On peut montrer que Ag est, en fait, ??gale ?? la diff??rence entre la les potentiels chimiques des produits et ceux des r??actifs. Par cons??quent, la somme des ??nergies de Gibbs des r??actifs doit ??tre ??gale ?? la somme des ??nergies de Gibbs des produits.
o?? μ est dans ce cas une molaire partielle d'??nergie Gibbs, un le potentiel chimique. Le potentiel chimique d'un r??actif A est une fonction de la activit??, {A} de ce r??actif.
En substituant les expressions de ce genre dans l' ??quation de l'??nergie Gibbs :
, ?? la pression et la temp??rature constante devient:
r??sulte en:
En substituant les potentiels chimiques:
la relation devient:
A l'??quilibre, 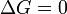 et donc
et donc
menant ??:
Ag O m est la molaire Gibbs changement d'??nergie standard pour la r??action et K est le la constante d'??quilibre. A noter que les activit??s et les constantes d'??quilibre sont des nombres sans dimension.
Traitement de l'activit??
L'expression de la constante d'??quilibre peut ??tre r????crite comme ??tant le produit d'un quotient de la concentration, K c et un activit?? coefficient quotient, Γ.
[A] est la concentration du r??actif A, etc. Il est possible en principe d'obtenir des valeurs de coefficients d'activit??, γ. Pour les solutions, les ??quations comme la Force ionique ou extensions comme Davies ??quation ou les ??quations Pitzer peuvent ??tre utilis??s. Logiciel (ci-dessous). Cependant ce ne est pas toujours possible. Il est courant de penser que Γ est une constante, et d'utiliser le quotient de la concentration en place de la constante d'??quilibre thermodynamique. Il est ??galement pratique g??n??rale ?? utiliser le terme constant de l'??quilibre au lieu de la concentration quotient plus pr??cis. Cette pratique sera suivie ici.
Pour les r??actions en phase gazeuse, pression partielle est utilis??e ?? la place de la concentration et coefficient de fugacit?? en place du coefficient d'activit??. Dans le monde r??el, par exemple, lors de la prise l'ammoniac dans l'industrie, les coefficients de fugacit?? doit ??tre prise en compte. Fugacit??, f, est le produit de la pression partielle et le coefficient de fugacit??. Le potentiel chimique d'une esp??ce dans la phase gazeuse est donn??e par
si l'expression g??n??rale d??finissant une constante d'??quilibre est valable pour les deux phases de la solution et de gaz.
Justification de l'utilisation des quotients de concentration
En solution aqueuse, les constantes d'??quilibre sont habituellement d??termin??es en pr??sence d'un ??lectrolyte "inerte" tel que nitrate de sodium NaNO 3 ou Le perchlorate de potassium KClO 4. Le la force ionique, I, d'une solution contenant un sel dissous, X + Y -, est donn??e par
o?? c repr??sente la concentration, z signifie charge ionique et la somme est prise sur toutes les esp??ces en ??quilibre. Lorsque la concentration du sel dissous est beaucoup plus ??lev??e que les concentrations des r??actifs d'analyse, la force ionique est effectivement constante. ??tant donn?? que les coefficients d'activit?? d??pendent de la force ionique des coefficients d'activit?? de l'esp??ce sont effectivement ind??pendante de la concentration. Ainsi, l'hypoth??se selon laquelle Γ est constante est justifi??e. Le quotient de la concentration est un multiple simple de la constante d'??quilibre.
Toutefois, K c varie avec la force ionique. Si elle est mesur??e ?? une s??rie de forces ioniques diff??rentes, la valeur peut ??tre extrapol??e ?? z??ro de la force ionique. Le quotient de concentration obtenu de cette mani??re est connue, paradoxalement, ?? la constante d'??quilibre thermodynamique.
Pour utiliser la valeur publi??e d'une constante d'??quilibre dans des conditions de force ionique diff??rentes des conditions utilis??es dans sa d??termination, la valeur doit ??tre ajust??e Logiciel (ci-dessous).
M??langes m??tastables
Un m??lange peut ??tre ne semblent pas avoir tendance ?? changer, mais il ne est pas ?? l'??quilibre. Par exemple, un m??lange de SO 2 et O 2 est m??tastable car il ya une barri??re cin??tique de formation du produit, SO 3.
- 2SO 2 + O 2
 2SO 3
2SO 3
La barri??re peut ??tre surmont??e quand un catalyseur est ??galement pr??sent dans le m??lange comme dans le processus contacter, mais le catalyseur ne affecte pas les concentrations ?? l'??quilibre.
De m??me, la formation de bicarbonate de dioxyde de carbone et eau est tr??s lente dans des conditions normales
- CO 2 + 2H 2 O
 HCO 3 - + H 3 O +
HCO 3 - + H 3 O +
mais presque instantan??e en pr??sence du catalyseur enzyme anhydrase carbonique.
Compos??s purs dans ??quilibres
Lorsque des substances pures (liquides ou solides) sont impliqu??s dans les ??quilibres qu'ils ne apparaissent pas dans l'??quation d'??quilibre
L'application de la formule g??n??rale pour une constante d'??quilibre pour le cas sp??cifique de l'acide ??thano??que on obtient
On peut supposer que la concentration de l'eau est constante. Cette hypoth??se sera solutions valables pour tous, mais tr??s concentr??s. L'expression constante d'??quilibre est donc g??n??ralement ??crit comme
o?? maintenant
![K = K_C * [H_2O] \,](../../images/117/11727.png)
un facteur constant est incorpor?? dans la constante d'??quilibre.
Un cas particulier est le auto-ionisation d'elle-m??me de l'eau
La constante Autoprotolyse est d??fini comme
![K_w = [^ H +] [^ OH -] \,](../../images/117/11729.png)
Il est parfaitement l??gitime d'??crire [H +] pour le concentration d'ions hydronium, depuis l'??tat de la solvatation du proton est constante (en solution dilu??e) et ainsi ne affecte pas les concentrations ?? l'??quilibre. K w varie avec la variation de la r??sistance et / ou la temp??rature ionique.
Les concentrations de H + et OH - ne sont pas des quantit??s ind??pendantes. Le plus souvent [OH -] est remplac?? par K w [H +] -1 dans des expressions constantes d'??quilibre qui, autrement, l'hydroxyde .
Solides ??galement ne apparaissent pas dans l'??quation d'??quilibre. Un exemple est le Boudouard r??action:
pour laquelle l'??quation (sans carbone solide) se ??crit:
??quilibres multiples
Prenons le cas d'un acide dibasique H 2 A. Lorsqu'il est dissous dans l'eau, le m??lange va contenir H 2 A, HA - et A 2. Cet ??quilibre peut ??tre divis??e en deux ??tapes, dans chacune desquelles un proton est lib??r??.
K 1 et K 2 sont des exemples de constantes d'??quilibre par ??tapes. La constante d'??quilibre global,  , Est produit par ??tapes des constantes.
, Est produit par ??tapes des constantes.
On notera que ces constantes sont constantes de dissociation parce que les produits sur le c??t?? droit de l'expression d'??quilibre sont des produits de dissociation. Dans de nombreux syst??mes, il est pr??f??rable d'utiliser des constantes d'association.
β 1 et β 2 sont des exemples de constantes d'association. Il est clair que β 1 = 1 / K 2 et β 2 = 1 / β D; lg = pK β 1 et 2 β 2 = lg pK 2 + pK 1
Effet de la variation de temp??rature sur une constante d'??quilibre
L'effet des changements de temp??rature sur une constante d'??quilibre est donn?? par la Relation de Van't Hoff
Ainsi, par r??actions exothermiques, (AH est n??gatif) K diminue avec la temp??rature, mais, pour r??actions endothermiques, (AH est positif) K augmente avec la temp??rature. Une formulation alternative est
A premi??re vue, cela semble offrir un moyen d'obtention de la norme enthalpie molaire de la r??action par l'??tude de la variation de K avec la temp??rature. En pratique, cependant, le proc??d?? ne est pas fiable parce que la propagation d'erreur donne presque toujours de tr??s grandes erreurs sur les valeurs calcul??es de cette fa??on.
Types d'??quilibre et certaines applications
- Dans la phase gazeuse. Les moteurs de fus??e
- La synth??se industrielle tels que l'ammoniac dans le Proc??d?? Haber-Bosch (repr??sent?? ?? droite) a lieu ?? travers une succession d'??tapes d'??quilibre, y compris les processus de l'adsorption.
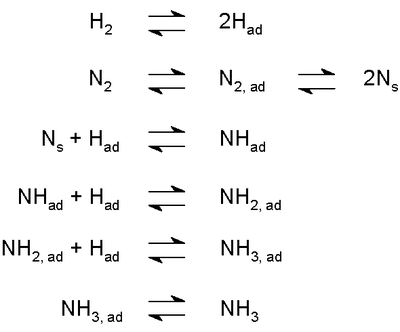
- la chimie atmosph??rique
- L'eau de mer et d'autres eaux naturelles: Oc??anographie chimique
- La distribution entre deux phases
- Coefficient logD-Distribution: Important pour les produits pharmaceutiques o?? lipophile est une propri??t?? importante d'un m??dicament
- L'extraction liquide-liquide, L'??change d'ions, la chromatographie
- produit de solubilit??
- Absorption et la lib??ration de l'oxyg??ne par h??moglobine dans le sang
- ??quilibres acide / base: Acid constante de dissociation, hydrolyse, des solutions tampons, indicateurs, hom??ostasie acido-basique
- M??tal-ligand de complexation: des agents s??questrants, la th??rapie de ch??lation, R??actifs de contraste IRM, Schlenk ??quilibre
- La formation d'adduits: La chimie h??te-invit??, la chimie supramol??culaire, reconnaissance mol??culaire, t??troxyde de diazote
- Dans certaines r??actions oscillants, l'approche ?? l'??quilibre ne est pas asymptotiquement mais sous la forme d'une oscillation amortie.
- La connexes ??quation de Nernst en ??lectrochimie donne la diff??rence de potentiel d'??lectrode en fonction de la concentration d'oxydo-r??duction.
- Lorsque les mol??cules de chaque c??t?? de l'??quilibre sont capables de r??agir de mani??re irr??versible en outre dans des r??actions secondaires, le rapport final du produit est d??termin?? en fonction de la Curtin-Hammett principe.
Dans ces applications, des termes tels que la stabilit?? constante, constante de formation, constante de liaison, constante d'affinit??, d'association / constante de dissociation sont utilis??s. En biochimie, il est courant de donner unit??s pour les constantes de liaison, qui servent ?? d??finir les unit??s de concentration utilis??es lorsque la valeur de la constante a ??t?? d??termin??e.
Composition d'un m??lange ?? l'??quilibre
Quand le seul ??quilibre est celui de la formation d'un adduit 1: 1 comme la composition d'un m??lange, il existe un certain nombre de fa??ons dont la composition d'un m??lange peut ??tre calcul??e. Par exemple, voir table de glace pour une m??thode traditionnelle de calcul du pH d'une solution d'un acide faible.
Il existe trois approches pour le calcul g??n??rale de la composition d'un m??lange ?? l'??quilibre.
- L'approche la plus fondamentale est de manipuler les diff??rentes constantes d'??quilibre jusqu'?? ce que les concentrations d??sir??es sont exprim??s en termes de constantes d'??quilibre mesur??es (??quivalent ?? la mesure de potentiels chimiques) et les conditions initiales.
- Minimiser l'??nergie Gibbs du syst??me.
- Satisfaire l'??quation de bilan de masse. Les ??quations de bilan de masse sont tout simplement des d??clarations qui d??montrent que la concentration totale de chaque r??actif doit ??tre constante par la loi du conservation de la masse.
R??solvant les ??quations de bilan massique
En g??n??ral, les calculs sont un peu compliqu??. Par exemple, dans le cas d'un acide dibasique, H 2 A dissous dans l'eau les deux corps r??actionnels peuvent ??tre sp??cifi??s comme le de base conjugu??, A 2, et de la protons, H +. Les ??quations suivantes de bilan de masse pourraient se appliquer tout aussi bien ?? une base telle que Le 1,2-diamino??thane, auquel cas la base elle-m??me est d??sign?? comme r??actif A:
Avec T A la concentration totale des esp??ces A. A noter qu'il est d'usage d'omettre les charges ioniques lors de l'??criture et l'utilisation de ces ??quations.
Lorsque les constantes d'??quilibre sont connus et les concentrations totales sont sp??cifi??s il ya deux ??quations ?? deux "concentrations libres" inconnus [A] et [H]. Cela d??coule du fait que [HA] = β 1 [A] [H], [H 2 A] = β 2 [A] [H] 2 et [OH] = K w [H] -1
de sorte que les concentrations des "complexes" sont calcul??s ?? partir des concentrations libres et les constantes d'??quilibre. Expressions g??n??rales applicables ?? tous les syst??mes avec deux r??actifs, A et B seraient
Il est facile de voir comment cela peut ??tre port??e ?? trois ou plusieurs r??actifs.
Composition de polyacides en tant que fonction du pH
Composition selon l'une des solutions contenant des r??actifs A et H est facile de calculer en fonction de p [H]. Lorsque [H] est connu, la concentration libre [A] est calcul??e ?? partir de l'??quation du bilan massique dans A. Voici un exemple des r??sultats qui peuvent ??tre obtenus.

Ce sch??ma, pour l'hydrolyse de l' aluminium Acide de Lewis Al 3+ aq montre les concentrations d'esp??ces pour une solution 5 M ?? 10 -6 d'un sel d'aluminium en tant que fonction du pH. Chaque concentration est indiqu??e en pourcentage de l'aluminium total.
??quilibres de solution avec pr??cipitations
Le diagramme ci-dessus illustre le point que pr??cipiter ce ne est pas l'une des principales esp??ces dans l'??quilibre de la solution peut ??tre form??e. A pH 5,5 juste au-dessous les principales esp??ces pr??sentes dans une solution 5 uM de Al 3+ sont des hydroxydes d'aluminium Al (OH) 2+, Al (OH) 2 + et Al 13 (OH) 32 7+, mais sur l'??l??vation du pH Al (OH) 3 pr??cipit?? de la solution. Cela se produit parce que Al (OH) 3 a une tr??s grande ??nergie treillis. Lorsque le pH se ??l??ve de plus en plus Al (OH) 3 sort de la solution. Ceci est un exemple de Le principe de Le Chatelier en action: L'augmentation de la concentration de l'ion hydroxyde provoque plus de l'hydroxyde d'aluminium pour pr??cipiter, ce qui ??limine l'hydroxyde de la solution. Lorsque la concentration en soude est suffisamment ??lev??e l'aluminate soluble, Al (OH) 4 -, est form??e.
Un autre exemple commun o?? se produit la pr??cipitation est quand un cation m??tallique interagit avec un ligand anionique pour former un complexe ??lectriquement neutre. Si le complexe est hydrophopbic, il va pr??cipiter hors de l'eau. Cela se produit avec le nickel ions Ni 2+ et dim??thylglyoxime, (dmgH 2): dans ce cas l'??nergie de r??seau du solide ne est pas particuli??rement grande, mais il d??passe largement l'??nergie la solvatation de la mol??cule Ni (dmgH) 2.
Minimisation de l'??nergie Gibbs
A l'??quilibre, G est au minimum:
Pour un syst??me ferm??, pas de particules peuvent entrer ou sortir, m??me se ils peuvent se combiner de diff??rentes fa??ons. Le nombre total d'atomes de chaque ??l??ment restera constant. Cela signifie que la r??duction ci-dessus doivent ??tre soumis ?? des contraintes:
o?? 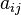 est le nombre d'atomes de l'??l??ment i dans la mol??cule et b j i 0 est le nombre total d'atomes de l'??l??ment i, qui est une constante, ??tant donn?? que le syst??me est ferm??. Se il ya un total de types d'atomes dans le syst??me k, alors il y aura k ces ??quations.
est le nombre d'atomes de l'??l??ment i dans la mol??cule et b j i 0 est le nombre total d'atomes de l'??l??ment i, qui est une constante, ??tant donn?? que le syst??me est ferm??. Se il ya un total de types d'atomes dans le syst??me k, alors il y aura k ces ??quations.
Ce est un probl??me classique dans optimisation, appel??e minimisation sous contrainte. La m??thode la plus courante de la r??solution qu'il utilise le proc??d?? de Multiplicateurs de Lagrange, aussi connu comme multiplicateurs ind??termin?? (bien que d'autres proc??d??s peuvent ??tre utilis??s).
D??finir:
o?? le  sont des multiplicateurs de Lagrange, une pour chaque ??l??ment. Cela permet ?? chacun de la
sont des multiplicateurs de Lagrange, une pour chaque ??l??ment. Cela permet ?? chacun de la  ?? traiter de fa??on ind??pendante, et il peut ??tre d??montr?? en utilisant les outils de calcul ?? variables multiples que la condition d'??quilibre est donn??e par
?? traiter de fa??on ind??pendante, et il peut ??tre d??montr?? en utilisant les outils de calcul ?? variables multiples que la condition d'??quilibre est donn??e par
 et
et 
(Pour preuve voir Multiplicateurs de Lagrange)
Il se agit d'un ensemble d'??quations inconnues ?? (m + k) (m + k) (la  et le
et le  ) Et peut donc ??tre r??solu pour les concentrations ?? l'??quilibre
) Et peut donc ??tre r??solu pour les concentrations ?? l'??quilibre  pour autant que les potentiels chimiques sont connus en tant que fonctions des concentrations ?? la temp??rature et une pression donn??es. (Voir Bases de donn??es thermodynamiques pour les substances pures).
pour autant que les potentiels chimiques sont connus en tant que fonctions des concentrations ?? la temp??rature et une pression donn??es. (Voir Bases de donn??es thermodynamiques pour les substances pures).
Cette m??thode de calcul des concentrations chimiques d'??quilibre est utile pour les syst??mes avec un grand nombre de mol??cules diff??rentes. L'utilisation des ??quations de conservation atomiques de l'??l??ment k de la contrainte de masse est simple, et remplace l'utilisation des ??quations des coefficients stoechiom??triques.


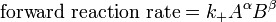





![K_C = \ frac {[S] ^ \ sigma [T] ^ \ tau} {[A] ^ \ alpha [B] ^ \ beta}](../../images/117/11709.png)



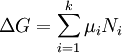
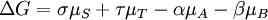




![K = \ frac {{[S]} ^ \ sigma {[T]} ^ \ tau ...} {{[A]} ^ \ alpha {[B]} ^ \ beta ...} \ times \ frac {{\ gamma_S} ^ \ sigma {\ gamma_T} ^ \ tau ...} {{\ gamma_A} ^ \ alpha {\ gamma_B} ^ \ beta ...} = K_C \ Gamma](../../images/117/11719.png)

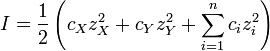
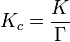

![K_C = \ frac {[{} ^ CH_3CO_2 -] [{} ^ H_3O +]} {[{} CH_3CO_2H] [{} H_2O]}](../../images/117/11725.png)
![K = \ frac {[{} ^ CH_3CO_2 -] [{} ^ H_3O +]} {[{} CH_3CO_2H]}](../../images/117/11726.png)


![K_C = \ frac {[CO_2]} {[CO] ^ 2}](../../images/117/11731.png)
![H_2A \ rightleftharpoons HA ^ - ^ + H +: K_1 = \ frac {[HA ^ -] [^ H +]} {[H_2A]}](../../images/117/11732.png)
![HA ^ - \ rightleftharpoons A ^ {2-} ^ + H +: K_2 = \ frac {[A ^ {2 -}] [^ H +]} {[HA ^ -]}](../../images/117/11733.png)
![A d'H_2A \ ^ {2-} + 2H + ^: \ beta_D = \ frac {[A ^ {2 -}] [^ H +] ^ 2} {[H_2A]} = K_1K_2](../../images/117/11735.png)
![A ^ {2-} + H ^ + \ rightleftharpoons HA ^ -: \ beta_1 = \ frac {[HA ^ -]} {[A ^ {2 -}] [^ H +]}](../../images/117/11736.png)
![A ^ {2-} + 2H ^ + \ rightleftharpoons H_2A: \ beta_2 = \ frac {[H_2A]} {[A ^ {2 -}] [^ H +] ^ 2}](../../images/117/11737.png)


![T_A = [A] + [HA] + [H_2A] \,](../../images/117/11744.png)
![T_H = [H] + [HA] + 2 [H_2A] - [OH] \,](../../images/117/11745.png)
![T_A = [A] + \ beta_1 [A] [H] + \ beta_2 [A] [H] ^ 2 \,](../../images/117/11746.png)
![T_H = [H] + \ beta_1 [A] [H] + 2 \ beta_2 [A] [H] ^ 2 - K_w [H] ^ {- 1} \,](../../images/117/11747.png)
![T_A = [A] + \ {sum_i p_i \ beta_i [A] ^ {} p_i [B] ^ {}} Q_i](../../images/117/11748.png)
![T_B = [B] + \ {sum_i Q_i \ beta_i [A] ^ {} p_i [B] ^ {}} Q_i](../../images/117/11749.png)



