Module de Young
Le module de Young ou module d’élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et le début de la déformation d'un matériau élastique isotrope.
Le physicien britannique Thomas Young (1773-1829) avait remarqué que le rapport entre la contrainte de traction appliquée à un matériau et la déformation qui en résulte (un allongement relatif) est constant, tant que cette déformation reste petite et que la limite d'élasticité du matériau n'est pas atteinte.
La loi d'élasticité est la loi de Hooke, c'est-à-dire 
, où :
-
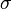est la contrainte (en unité de pression) ; -
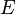est le module de Young (en unité de pression) ; -
est l'allongement relatif, ou déformation (adimensionnel).
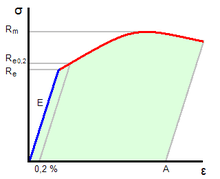
Le module de Young est la contrainte mécanique qui engendrerait un allongement de 100 % de la longueur initiale d'un matériau (il doublerait donc de longueur), si l'on pouvait l'appliquer réellement : dans les faits, le matériau se déforme de façon permanente, ou se rompt, bien avant que cette valeur ne soit atteinte. Le module de Young est la pente initiale du diagramme de déformation-contrainte.
Un matériau dont le module de Young est très élevé est dit rigide. L'acier, l'iridium, le diamant, sont des matériaux très rigides, l'aluminium et le plomb le sont moins. Les matières plastiques et organiques, les mousses sont généralement peu rigides, on dit qu'elles sont souples, élastiques ou flexibles (pour un effort de flexion).
N. B. Ne pas confondre :
- rigidité et résistance : la résistance mécanique d'un matériau est caractérisée par sa limite d'élasticité et/ou sa résistance à la traction ;
- rigidité et raideur : la raideur d'une poutre (par exemple) dépend de son module de Young (de sa rigidité) mais aussi du rapport de sa section à sa longueur[1]. La rigidité caractérise les matériaux, la raideur concerne les produits et les constructions : une pièce mécanique massive en matière plastique peut être beaucoup plus raide qu'un ressort en acier ;
- rigidité et dureté : la dureté d'un matériau définit la résistance relative qu'oppose sa surface à la pénétration d'un corps plus dur.
Le tenseur des rigidités généralise le module de Young aux matériaux anisotropes.
Unités
D'après l'équation aux dimensions, le module de Young est homogène à une pression, ou plus précisément une contrainte. L'unité internationale est donc le pascal (Pa). En raison des valeurs élevées que prend ce module, il est en général exprimé en gigapascals (GPa) ou mégapascals (MPa).
Expressions théoriques
Dans le cas d'un matériau cristallin et certains matériaux amorphes, le module de Young exprime la « force de rappel » électrostatique qui tend à maintenir les atomes à distance constante. Il peut s'exprimer en fonction de la dérivée seconde du potentiel interatomique.
Dans le système d'unités « naturelles » atomique, le module de Young, pour un matériau isotrope, est homogène à[2]
où
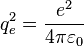
et où
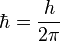
est la constante de Planck réduite.
Cela dit, compte tenu des problèmes où il apparaît (bilaplacien), il paraît assez naturel de le rationaliser :
- soit comme
; - soit comme
,
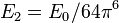les ordres de grandeur de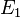 
ou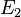 
sont à comparer aux valeurs tabulées, de l'ordre de 100 GPa, qui apparaissent alors relever de ce corpus théorique.
Dans le cas des polymères, l'agitation thermique « tortille » la chaîne carbonée qui tend à maintenir la longueur de la chaîne constante. Le module de Young peut alors s'exprimer en fonction de l'entropie.
Cette différence de comportement est flagrante lorsque l'on considère l'influence de la température ; si l'on soumet une éprouvette à une charge constante (essai de fluage) :
- lorsque l'on augmente la température, une éprouvette de métal s'allonge (dilatation), donc son module de Young diminue, tandis que l'éprouvette en polymère se raccourcit (les chaînes s'agitent, s'entortillent) donc son module de Young augmente[réf. nécessaire] ;
- lorsque l'on diminue la température, on observe le phénomène inverse : l'éprouvette de métal se raccourcit (contraction) donc son module de Young augmente, tandis que l'éprouvette de polymère s'allonge (les chaînes sont moins agitées et se laissent étirer) donc son module de Young diminue[réf. nécessaire].
Relations
- La relation entre le module de cisaillement (
) et le coefficient de Poisson (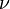
) s'écrit 
.
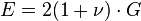- La relation entre
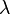et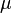 
, appelés coefficients de Lamé, est
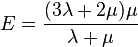.Méthodes de mesure du module de Young
Le plus simple reste bien sûr de réaliser un essai de traction. Et, connaissant les dimensions de l'éprouvette, d'en déduire le module de Young 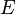. Cependant, il est difficile de réaliser cette mesure avec une bonne précision.
C'est pourquoi on préfère, lorsque cela est possible, déduire le module de Young de la fréquence propre de vibration d'une tige de matériau maintenue à ses extrémités et chargée en son milieu.
On peut aussi mesurer la vitesse du son dans le matériau qui nous intéresse, et en déduire le module de Young sachant qu'on a la relation suivante
.Cependant, cette loi est approchée : la vitesse du son dépend aussi du coefficient de Poisson.
Le module de Young augmente avec la vitesse de déformation. Voir aussi Principe d'équivalence temps-température.
Le module de Young complexe peut être déterminé par analyse mécanique dynamique.
Quelques valeurs numériques de modules de Young
Les caractéristiques mécaniques des matériaux sont variables d'un échantillon à l'autre. D'un point de vue global, selon M. Ashby, on trouve des matériaux dont la valeur est comprise entre 10 kPa (mousses) et 1 000 GPa (céramiques techniques).
|
|
|
N.B. Ces valeurs sont celles du module d'élasticité dans le sens parallèle au fil (matériau anisotrope). Dans une même essence, celui-ci varie en fonction de l'humidité, de la densité (qui n'est pas constante) et d'autres caractéristiques (longueur des fibres…). |
|
|
Utilisations
En médecine, la mesure des variations du module de Young dans un organe est une possibilité de l'imagerie médicale qui permet de représenter l'élasticité des tissus même profonds, par exemple pour donner l'étendue de la fibrose d'un foie ou détecter dans un sein un carcinome petit ou profond, peu décelable à la palpation (élastographie de 2e génération).
Articles connexes
- Module élastique
- Facteur de forme
- Module de cisaillement
- Mécanique des milieux continus
- Élinvar
Références
- ↑ Sophie Trachte, Matériau, matière d'architecture soutenable : Choix responsable des matériaux de construction..., Presse universitaire de Louvain, coll. « Thèse », , 534 p. (ISBN 2875580817), p. 75
- ↑ Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], [détail des éditions], chap. 3.
Bibliographie
- Ch. Kittel, Physique du solide, éd. Dunod, chap. Constantes d'élasticité.
- Michael F. Ashby, David R. H. Jones, Matériaux 1. Propriétés et applications, éd. Dunod, chap. 3 : Les constantes d'élasticité.
Portail des sciences des matériaux 
Portail de la physique