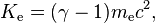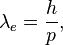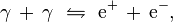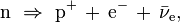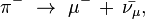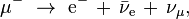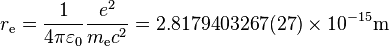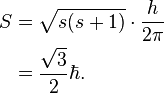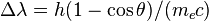Électron

Des expériences menées avec les tubes de Crookes ont démontré avec certitude l'existence de l'électron.
Dans cette photo, le tube est rempli d'un gaz à basse pression. Une tension électrique élevée est appliquée entre la cathode (à l'extrémité gauche) et l'anode (à l'extrémité du coude sous le tube). À la cathode, cette tension fait naître un faisceau d'électrons qui se déplacent en ligne droite (la faible lueur bleue au centre du tube), tant qu'ils ne heurtent pas d'atomes de gaz. À la droite, une pièce métallique en forme de croix de Malte bloque en partie ce flux d'électrons, ce qui crée une ombre à l'extrémité droite. Les autres électrons frappent le fond du tube et le rendent en partie luminescent (lueur vert pâle). Dans le coude sous le tube, le gaz s'illumine (lueur bleue) au passage des électrons déviés, collectés par l'anode[1].
| Classification | |
|---|---|
| Famille | |
| Groupe |
Lepton |
| Génération |
1re |
| Interaction(s) | |
| Symbole |
e- β- (particule β) |
| Nbr. de types |
1 |
| Antiparticule |
positron |
| Masse | |
|---|---|
| Charge électrique | |
| Moment magnétique |
9,274×10-24 J/T |
| Spin |
½ |
| Parité |
+1 |
| Durée de vie |
> 1,45×1034 s |
| Prédiction |
Richard Laming (1838–1851), George Stoney (1874) et d'autres |
|---|---|
| Découverte |
1897 |
| Découvreur |
L'électron est une particule élémentaire qui possède une charge élémentaire de signe négatif et est l'un des composants de l'atome avec les neutrons et les protons. Il est fondamental en chimie, car il participe à presque tous les types de réactions chimiques et constitue un élément primordial des liaisons présentes dans les molécules. En physique, l'électron intervient dans une multitude de rayonnements et d'effets. Ses propriétés, qui se manifestent à l'échelle microscopique, expliquent la conductivité électrique, la conductivité thermique, l'effet Vavilov-Tcherenkov, l'incandescence, l'induction électromagnétique, la luminescence, le magnétisme, le rayonnement électromagnétique, la réflexion optique et la supraconductivité, phénomènes macroscopiques largement exploités dans les pays industrialisés. Possédant la plus faible masse de toutes les particules chargées, il sert régulièrement à l'étude de la matière.
Le concept d'une quantité indivisible de charge électrique est élaboré à partir de 1838 par le naturaliste britannique Richard Laming afin d'expliquer les propriétés chimiques des atomes. L'électron est identifié comme le corpuscule envisagé par Joseph John Thomson et son équipe de physiciens britanniques en 1897, à la suite de leurs travaux sur les rayons cathodiques.
C'est à cette époque que Thomson propose son modèle atomique. En 1905, Albert Einstein propose une explication de l'effet photoélectrique — des électrons émis par la matière sous l'influence de la lumière — qui servira d'argument en faveur de la théorie des quanta. En 1912, Niels Bohr explique les raies spectrales en postulant la quantification de l'orbite des électrons de l'atome hydrogène, autre argument soutenant cette théorie. En 1914, les expériences d'Ernest Rutherford et d'autres ont solidement établi la structure de l'atome comme un noyau positivement chargé entouré d'électrons de masse plus faible. En 1923, les résultats expérimentaux d'Arthur Compton convainquent une majorité de physiciens de la validité de la théorie des quanta. En 1924, Wolfgang Pauli définit le principe d'exclusion de Pauli, ce qui implique que les électrons possèdent un spin. La même année, Louis de Broglie émet l'hypothèse, vérifiée plus tard, que les électrons présentent une dualité onde-corpuscule. En 1928, Paul Dirac publie son modèle de l'électron qui l'amènera à prédire l'existence du positron puis de l'antimatière. D'autres études des propriétés de l'électron ont mené à des théories plus complètes de la matière et du rayonnement.
Histoire

Les anciens Grecs ont déjà remarqué que l'ambre attire de petits objets quand elle est frottée avec de la fourrure ; en dehors de la foudre, ce phénomène est la plus ancienne expérience de l'humanité en rapport avec l'électricité[4], un déplacement de particules électriquement chargées.
En 1269, Pierre de Maricourt, un ingénieur militaire au service du prince français Charles Ier de Sicile, étudie les propriétés des aimants permanents. « Cette étude, qui nous a été transmise sous forme d'une lettre écrite à l'un de ses collègues, comprend la plupart des expériences élémentaires aujourd'hui décrites dans les manuels de physique. »[5] Dans son traité de 1600 De Magnete, le médecin anglais William Gilbert crée le mot bas-latin « electricus » pour désigner la propriété d'attirer les petits objets après frottement[6]. Le mot « électrique » dérive de l'anglais « electrick », qui dérive lui-même du latin « electricus » : « propre à l'ambre[7] ». Le mot latin ēlectrum dérive du grec ἤλεκτρον (êlectron´) désignant l'ambre.
Francis Hauksbee dans les années 1700 et C. F. du Fay en 1737 découvrent indépendamment deux sortes d'électricité : l'une obtenue en frottant du verre et l'autre engendrée en frottant de la résine. Du Fay en conclut que l'électricité peut se réduire à deux fluides électriques, « vitreux » et « résineux », que l'on sépare par frottement, et que l'on peut recombiner ensemble[8]. Une décennie plus tard, Benjamin Franklin soutient que l'électricité ne diffère pas des autres types de fluides électriques mais qu'il s'agit de la même chose, sous des pressions différentes. Il lui apporte la terminologie moderne de charge positive ou négative respectivemement[9],[10].
Entre 1838 et 1851, le naturaliste britannique Richard Laming développe l'idée qu'un atome est composé d'un noyau de matière, entouré de particules subatomiques qui ont une charge électrique unité[11]. À partir de 1846, le physicien allemand Wilhelm Eduard Weber défend la théorie que l'électricité est composée de fluides chargés positivement et négativement, et qu'une loi en carré inverse régit leur interaction[12]. Après avoir étudié l'électrolyse en 1874, le physicien irlandais George Stoney suggère qu'il existe « une seule quantité définie d'électricité » : la charge d'un ion monovalent. Ce postulat lui donne la capacité d'estimer la valeur de cette charge élémentaire e à partir des lois de l'électrolyse de Faraday[13]. Cependant, Stoney croit que ces charges sont attachées de façon permanente aux atomes, et ne peuvent donc leur être enlevées[14]. En 1881, le physicien allemand Hermann von Helmholtz est convaincu que les charges positives et négatives sont composées de parties élémentaires, chacune « se comportant comme des atomes d'électricité[15] ».
En 1894, Stoney invente le terme d'« électron » pour désigner ces charges élémentaires, écrivant « [...] une estimation a été faite de la valeur réelle de cette unité fondamentale très remarquable d'électricité, pour laquelle je me suis risqué à proposer le nom d'"électron" »[16]. Le mot électron est une combinaison du mot « électrique » et du suffixe « -on », ce dernier étant par la suite utilisé pour désigner une particule subatomique, comme le proton ou le neutron[17],[18].
Découverte

Pendant le XIXe siècle, les physiciens allemands Julius Plücker et Johann Wilhelm Hittorf étudient la conductivité électrique des gaz dans des ampoules de verre scellées munies d'une cathode et d'une anode[19] qui permettent de soumettre le gaz à un courant électrique. En 1869, Hittorf observe l'émission, par la cathode, de « faisceaux de particules » chargées si l'ampoule contient un gaz à basse pression[20],[21]. En 1876, le physicien allemand Eugen Goldstein montre que les rayons de cette lueur provoquent une ombre, et il les appelle rayons cathodiques[22]. Pendant les années 1870, le chimiste et physicien anglais William Crookes met au point le premier tube à rayons cathodiques avec un vide poussé à l'intérieur — nommé par la suite « tube de Crookes[23] ». Puis il montre que les rayons lumineux apparaissant dans le tube transmettent de l'énergie, et se déplacent de la cathode vers l'anode. De plus, en appliquant un champ magnétique, il est capable de défléchir les rayons, montrant ainsi que le faisceau se comporte comme s'il était chargé[24],[25]. En 1879, il propose d'expliquer ces propriétés par ce qu'il appelle « matière radiante ». Il estime qu'il s'agit d'un quatrième état de la matière, consistant en molécules chargées négativement, projetées à grande vitesse de la cathode[26].
Le physicien britannique né allemand Arthur Schuster développe les expériences de Crookes en disposant des plaques métalliques parallèlement aux rayons cathodiques, par lesquelles il peut appliquer différents potentiels électriques. Le champ électrique défléchit les rayons vers la plaque chargée positivement, ce qui renforce la preuve que les rayons portent une charge négative. En mesurant la déflexion selon la différence de potentiel, Schuster est capable en 1890 de mesurer le rapport masse sur charge des composants des rayons. Cependant, son calcul donne une valeur plus de mille fois inférieure à la valeur attendue, si bien que les contemporains n'accordent que peu de confiance à son calcul[24],[27]. En 1895, le thésard et futur physicien français Jean Perrin établit expérimentalement la nature corpusculaire de l'électron, alors que plusieurs scientifiques de cette époque considèrent l'électron comme une onde[28],[29].
En 1896-1897, le physicien britannique Joseph John Thomson et ses collègues John Townsend et Harold A. Wilson réalisent des expériences indiquant que les rayons cathodiques sont effectivement des particules individualisées, plutôt que des ondes, des atomes ou des molécules comme les spécialistes le croient à l'époque[30],[31]. Thomson fait de bonnes estimations à la fois de la charge e et de la masse m, trouvant que les particules des rayons cathodiques, qu'il appelle « corpuscules », ont environ un millième de la masse de l'ion le plus léger connu alors : l'hydrogène[32]. Il montre que le rapport charge sur masse e/m est indépendant de la matière de la cathode. Il montre de plus que les particules chargées négativement produites par les matériaux radioactifs, les matières chauffées et les matières illuminées sont les mêmes[33]. Son travail considérable sur la déflexion des rayons cathodiques dans un champ électrique est probablement la raison pour laquelle on lui attribue la découverte de l'électron[34],[35],[36]. Le nom d'électron est proposé à nouveau par le physicien irlandais George F. Fitzgerald, cette fois avec succès[24]. Historiquement, l'électron est la première particule élémentaire mise en évidence[37].

En 1900, Paul Drude propose de considérer l'ensemble des électrons d'un métal comme un gaz parfait. Il parvient alors à justifier théoriquement une conclusion expérimentale selon laquelle les bons conducteurs électriques sont aussi de bons conducteurs thermiques. Même si son hypothèse est fausse selon les connaissances actuelles, ce concept de « gaz parfait d'électrons » est encore utilisé en mécanique quantique[38].
En étudiant les minéraux naturellement fluorescents, le physicien français Henri Becquerel découvre que ceux-ci émettent des rayonnements en l'absence de toute source d'énergie externe. Ces matériaux radioactifs provoquent l'engouement des scientifiques, y compris celui du physicien néo-zélandais Ernest Rutherford, qui découvre qu'ils émettent des particules. Il leur donne le nom de particules alpha, bêta et gamma, selon leur pouvoir de pénétration de la matière[39]. En 1900, Becquerel montre que les rayons bêta émis par le radium sont défléchis par un champ électrique, et que leur rapport masse sur charge est le même que celui des rayons cathodiques[40]. Ce résultat conforte l'idée que les électrons existent comme composants des atomes[41],[42].
La charge de l'électron est mesurée de façon plus précise par le physicien américain Robert Millikan par son expérience sur la goutte d'huile de 1909, dont il publie les résultats en 1911. Cette expérience utilise un champ électrique pour compenser la pesanteur et empêcher ainsi une goutte d'huile chargée de tomber. Ce système permet de mesurer la charge électrique depuis quelques ions jusqu'à 150, avec une marge d'erreur de moins de 0,3 %. Des expériences comparables ont été faites plus tôt par le groupe de Thomson, en utilisant des brouillards de gouttelettes d'eau chargées par électrolyse[30] et en 1911 par Abram Ioffé, qui a obtenu indépendamment le même résultat que Millikan en utilisant des microparticules de métal, et a publié ses résultats en 1913[43]. Cependant, les gouttes d'huile, moins volatiles, se prêtent mieux à des expériences de longue durée[44].
Vers le début du XXe siècle, des physiciens découvrent que, sous certaines conditions, une particule rapide provoque sur sa trajectoire la condensation de la vapeur d'eau sursaturée. En 1911, le physicien écossais Charles Thomson Rees Wilson, l'un des collaborateurs de Thomson[45], utilise cet effet pour mettre au point sa chambre à brouillard, qui permet de photographier les traces de particules chargées, comme des électrons rapides[46], ce qui facilite donc leur étude.
Théorie de l'atome
Les travaux du physicien néo-zélandais Ernest Rutherford, de 1909 à 1912, l'amènent à conclure que l'atome est constitué d'un petit noyau comprenant toute la charge positive et presque toute la masse de l'atome, noyau qui est entouré d'un nuage électronique[48],[49] (voir Expérience de Rutherford). Le physicien britannique Henry Moseley, qui travaille dans le laboratoire de Rutherford en 1913, établit avec certitude l'ordre des éléments chimiques dans le tableau périodique[50] (voir Loi de Moseley).
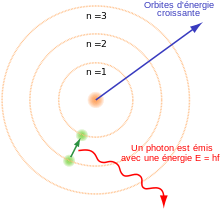
En 1913, le physicien danois Niels Bohr postule que les électrons sont dans des états quantifiés, dont l'énergie est déterminée par le moment angulaire autour du noyau. Les électrons peuvent passer d'un état à l'autre, par émission ou absorption de photons à des fréquences spécifiques. Au moyen de ces orbites quantifiées, il explique avec toute la précision requise les raies spectrales de l'atome d'hydrogène[51].
Les travaux des physiciens allemands James Franck et Gustav Hertz, de 1912 à 1914, prouvent la quantification des niveaux d'énergie des électrons dans les atomes et confirment donc les hypothèses du modèle de l'atome de Bohr[52] (voir Expérience de Franck et Hertz). Toutes ces expériences établissent solidement la structure de l'atome comme un noyau chargé positivement et entouré d'électrons de masse plus faible[53].
Cependant, le modèle de Bohr ne peut rendre compte des intensités relatives des raies spectrales, ni expliquer les spectres d'atomes plus complexes[53]. Malgré ces faiblesses, ce modèle atomique servira d'argument en faveur de la théorie des quanta[54].
Les liaisons chimiques entre atomes sont expliquées par Gilbert Lewis, qui propose en 1916 que la liaison covalente entre atomes est une paire d'électrons partagés[55]. Plus tard, en 1927, Walter Heitler et Fritz London expliquent complètement la formation des paires d'électrons et des liaisons chimiques en termes de mécanique quantique[56]. En 1919, le chimiste américain Irving Langmuir raffine le modèle statique d'atome de Lewis, et suggère que tous les électrons sont distribués sur des « couches concentriques (à peu près) sphériques, toutes de même épaisseur[57] ». Les couches sont à leur tour divisées en un certain nombre de cellules, chacune contenant une paire d'électrons. Avec ce modèle, Langmuir explique qualitativement les propriétés chimiques de tous les éléments du tableau périodique[56], que les scientifiques rapprochent selon la loi de similitude[58].
En 1924, le physicien autrichien Wolfgang Pauli remarque que la structure en couches de l'atome s'explique par le jeu de quatre paramètres qui définissent tous les états énergétiques, tant que chaque état n'est occupé que par un seul électron[59],[60]. Cette interdiction faite à deux électrons d'occuper le même état est devenue connue sous le nom de « principe d'exclusion de Pauli ». Le mécanisme déterminant le quatrième paramètre et ses deux valeurs, est fourni par les physiciens néerlandais Samuel Goudsmit et George Uhlenbeck, quand ils suggèrent que l'électron, outre le moment angulaire de son orbite, pourrait avoir un moment angulaire intrinsèque[53],[61]. Cette propriété devient notoire sous le nom de « spin » : elle explique le dédoublement des raies spectrales observé avec un spectrographe à haute résolution, qui est resté mystérieux jusque-là ; ce phénomène est connu sous le nom de structure hyperfine des raies[62]. Le principe de Pauli explique pourquoi la matière dite ordinaire crée ce qui est appelé le « volume » de la matière[63],[64],[65],[66],[67].
La mécanique quantique
Les électrons possèdent, comme toute la matière, la propriété quantique d'être à la fois ondes et corpuscules, si bien qu'ils peuvent avoir des collisions avec d'autres particules, et être diffractés comme la lumière. Cette dualité est facile à constater avec les électrons en raison de leur faible masse. Un électron, en raison de son spin, est un fermion, et satisfait donc au principe d'exclusion de Pauli[68].
En 1887, l'effet photoélectrique est observé par Heinrich Rudolf Hertz alors qu'il étudie les ondes électromagnétiques[69], et plusieurs scientifiques ont tenté d'en expliquer les mécanismes, sans résultat. Vingt ans plus tard, en 1905, Albert Einstein propose une première explication, qui lui vaudra le prix Nobel de physique de 1921[70]. Selon lui, des électrons sont émis par la matière seulement si la fréquence de la lumière est supérieure à un certain seuil. Pour y parvenir, il introduit le concept de photon, en utilisant celui de quantum d'énergie récemment proposé dans un tout autre contexte par Max Planck. L'explication d'Einstein sera l'un des premiers arguments en faveur de la théorie des quanta[71]. En 1923, Arthur Compton observe l'allongement de la longueur d'onde du photon causée par la diffusion qui porte son nom, laquelle est provoquée par l'interaction des photons et des électrons. « Ces résultats expérimentaux [sont] les premiers à convaincre la majorité des physiciens de la validité de la théorie quantique[72]. »
Dans sa publication Recherches sur la théorie des quanta, en 1924, le physicien français Louis de Broglie émet l'hypothèse que toute matière possède une onde de De Broglie semblable à la lumière[73]. C'est-à-dire que, selon les conditions, les électrons et autres particules matérielles montrent les propriétés soit de particules, soit d'ondes. Les propriétés corpusculaires d'une particule sont patentes quand elle apparaît à tout moment localisée à un endroit dans l'espace le long d'une trajectoire[74]. La nature ondulatoire est observée, par exemple, quand un faisceau passe à travers des fentes parallèles et crée des figures d'interférence. En 1927, l'effet d'interférence avec un faisceau d'électrons est montré par le physicien anglais George Paget Thomson, au moyen d'un mince film métallique, et par les physiciens américains Clinton Davisson et Lester Germer en utilisant un cristal de nickel[75].
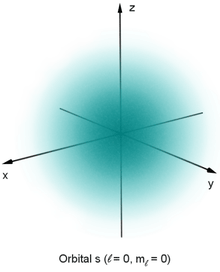
Le succès de la prédiction de De Broglie conduit à la publication par Erwin Schrödinger, en 1926, de l'équation de Schrödinger qui décrit avec succès la propagation des électrons en tant qu'onde[76]. Plutôt que de fournir une solution donnant la position d'un électron, cette équation d'onde peut être utilisée pour calculer la probabilité de trouver un électron dans un certain volume. Cette approche est ultérieurement nommée mécanique quantique, et donne une très bonne approximation des états d'énergie dans l'atome d'hydrogène[77]. Une fois le spin et les interactions entre les électrons pris en compte, la mécanique quantique modélise avec succès le comportement des électrons dans les atomes plus complexes que celui de l'hydrogène[78].
En 1928, améliorant le travail de Wolfgang Pauli[79], le physicien britannique Paul Dirac conçoit un modèle de l'électron — l'équation de Dirac — compatible avec la théorie de la relativité et la mécanique quantique[80]. Pour résoudre certaines lacunes de son équation relativiste, Dirac développe en 1930 un modèle de vide avec une mer infinie de particules d'énergie négative, parfois nommée « mer de Dirac ». Ceci le conduit à prédire l'existence du positron, équivalent de l'électron dans l'antimatière[81], « entité » physique également prédite par Dirac[82],[83]. Le positron est découvert par Carl D. Anderson, qui propose d'appeler les électrons standard « négatrons » et d'utiliser le terme « électron » comme terme générique pour désigner les deux charges sans distinction. Cet usage du terme « négatron » est encore rencontré à l'occasion, et peut être abrégée en « négaton »[84],[85].
En 1947, le physicien américain Willis Lamb, en collaboration avec le thésard Robert Retherford, découvre que certains états quantiques de l'atome d'hydrogène, qui devraient avoir la même énergie, se distinguent par un certain décalage[86], c'est le décalage de Lamb. À peu près au même moment, le physicien germano-américain Polykarp Kusch, travaillant avec Henry M. Foley, découvre que le moment magnétique de l'électron est un peu plus grand que celui prédit par la théorie de Dirac. Cet écart sera ultérieurement appelé « moment magnétique anomal » de l'électron. Pour résoudre ces problèmes, une théorie plus élaborée, appelée « électrodynamique quantique », est mise au point par Sin-Itiro Tomonaga, Julian Schwinger et Richard Feynman à la fin des années 1940[87],[88],[89].

- Niels Bohr : modèle atomique où les couches électroniques sont quantifiées (modèle de Bohr)
- Louis de Broglie : hypothèse, vérifiée, de la dualité onde-corpuscule de l'électron
- Arthur Compton : diffusion inélastique d'un photon sur un électron d'un atome (diffusion Compton)
- Paul Dirac : équation de Dirac, qui décrit le comportement de particules élémentaires de spins demi-entiers, comme les électrons
- Albert Einstein : explication de l'effet photoélectrique, une émission d'électrons sous l'influence de la lumière
- Charles-Eugène Guye : expériences qui démontrent la dépendance de la masse de l'électron à sa vitesse
- Wolfgang Pauli : principe d'exclusion de Pauli (les électrons ne peuvent pas se trouver au même endroit dans le même état quantique)
- Erwin Schrödinger : équation de Schrödinger, qui décrit l'évolution dans le temps d'une particule massive non relativiste, tel l'électron
- Charles Thomson Rees Wilson : chambre à brouillard, qui permet d'étudier différentes propriétés des particules, tels les électrons
Caractéristiques
Propriétés élémentaires
La masse d'un électron est approximativement 9,109×10-31 kg[2],[note 1], ou 5,489×10-4 unité de masse atomique[91]. Sur la base du principe d'équivalence masse-énergie d'Einstein, ceci correspond à une énergie de 511 keV[2],[note 2]. Le rapport entre les masses du proton et de l'électron est d'environ 1 836[note 3],[92],[93]. Les mesures astronomiques montrent que ce rapport n'a pas changé de façon mesurable pour la moitié de l'âge de l'Univers, comme prédit par le modèle standard[94].
L'électron a une charge électrique de -1,602×10-19 C[2],[note 4], qui est utilisée comme unité standard de charge pour les particules subatomiques. Selon la limite actuelle de la précision des expériences, la charge de l'électron est directement opposée à celle du proton[95]. Comme le symbole e est utilisé pour la charge élémentaire, le symbole de l'électron est e–, le signe – indiquant la charge de l'électron. L'antiparticule de l'électron[96], le positron, de symbole e+, est de charge électrique opposée[2],[97]. Ceci permet l'annihilation d'un électron avec un positron, en ne produisant que de l'énergie sous forme de rayons gamma[98],[99].
Selon le modèle standard, l'électron n'a pas de sous-composant connu[100], c'est donc une particule élémentaire[101],[102]. On le définit comme une particule ponctuelle avec une charge ponctuelle[68],[note 5]. L'observation d'un électron isolé dans un piège de Penning démontre que le rayon de cette particule est inférieur à 10-22 m[104]. Il y a bien pourtant une constante physique que l'on appelle « rayon classique de l'électron », dont la valeur bien plus grande est de 2,8179×10-15 m[note 6]. Cependant cette terminologie provient d'un calcul qui ignore les effets de la mécanique quantique ; en fait le soi-disant rayon classique de l'électron n'a pas grand-chose à voir avec une structure fondamentale de l'électron[106],[note 7]. Néanmoins, il donne un ordre de grandeur des dimensions pour lesquelles l'électrodynamique quantique devient importante pour comprendre la structure et le comportement de l'électron, notamment par la renormalisation.
Les scientifiques pensent, en s'appuyant sur des bases théoriques, que l'électron est stable : comme c'est la particule la plus légère de charge non nulle, sa désintégration violerait la conservation de la charge électrique[108]. Expérimentalement, la limite inférieure pour la vie moyenne de l'électron est de 1,45×1034 s, à un niveau de confiance de 90 %[109] (l'âge de l'univers est estimé à 4,34×1017 s[110]). L'électron diffère en cela des autres leptons chargés, le muon et le tauon, de courtes durées de vie[111].
L'électron a un moment angulaire intrinsèque, ou spin, de 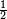 [2]. Cette propriété est généralement exprimée en appelant l'électron « particule de spin
[2]. Cette propriété est généralement exprimée en appelant l'électron « particule de spin 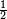 »[97]. Pour ce genre de particules, la valeur absolue du spin est
»[97]. Pour ce genre de particules, la valeur absolue du spin est 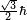 [note 8], tandis que le résultat de la mesure de la projection du spin sur n'importe quel axe ne peut être que ± ħ/2. Outre le spin, l'électron possède un moment magnétique le long de son spin[2]. Il est approximativement égal à un magnéton de Bohr[113],[note 9], qui est une constante physique égale à 9,274×10-24 J/T[2],[note 10]. La projection du spin sur la direction de la quantité de mouvement de l'électron définit la propriété connue sous le nom d'« hélicité »[114],[115].
[note 8], tandis que le résultat de la mesure de la projection du spin sur n'importe quel axe ne peut être que ± ħ/2. Outre le spin, l'électron possède un moment magnétique le long de son spin[2]. Il est approximativement égal à un magnéton de Bohr[113],[note 9], qui est une constante physique égale à 9,274×10-24 J/T[2],[note 10]. La projection du spin sur la direction de la quantité de mouvement de l'électron définit la propriété connue sous le nom d'« hélicité »[114],[115].
Propriétés quantiques

L'électron présente une dualité onde-particule, qui peut être démontrée par l'expérience des fentes d'Young. Cette propriété lui permet de passer à travers deux fentes parallèles simultanément, plutôt que juste une seule fente, comme cela serait le cas pour une particule classique[117]. En mécanique quantique, la propriété ondulatoire d'une particule peut être décrite mathématiquement comme une fonction à valeurs complexes, la fonction d'onde, couramment dénotée par la lettre grecque psi (ψ). Quand la valeur absolue de cette fonction est élevée au carré, cela donne la probabilité d'observer une particule dans un petit volume près de la position choisie — une densité de probabilité[118]. L'électron peut franchir une barrière de potentiel par effet tunnel, phénomène que la mécanique classique est incapable d'expliquer et que la mécanique quantique explique en faisant appel à la notion de fonction d'onde[119].
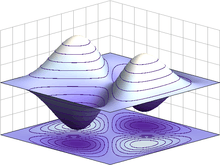
ψ(x1, x2) = √2[sin(πx1)sin(3πx2)] – sin(πx2)sin(3πx1)
Les électrons sont des particules indiscernables, parce qu'ils ne peuvent pas être distingués entre eux par leurs propriétés physiques intrinsèques. En mécanique quantique, ceci signifie qu'une paire d'électrons en présence doit pouvoir intervertir leur position sans provoquer de changement observable dans l'état du système. La fonction d'onde des fermions, notamment des électrons, est antisymétrique, c'est-à-dire qu'elle change de signe quand on échange deux électrons :
-
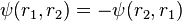 ,
,
où 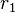 et
et 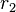 sont les positions des deux électrons. Comme la valeur absolue est invariable lors du changement de signe de la fonction, ceci indique que les probabilités sont les mêmes. Les bosons, tels les photons, ont des fonctions d'onde symétriques[118].
sont les positions des deux électrons. Comme la valeur absolue est invariable lors du changement de signe de la fonction, ceci indique que les probabilités sont les mêmes. Les bosons, tels les photons, ont des fonctions d'onde symétriques[118].
Dans le cas de l'antisymétrie, les solutions de l'équation d'onde pour des électrons en interaction résultent en une probabilité nulle que deux électrons occupent la même position, ou, en tenant compte du spin, le même état. C'est la cause du principe d'exclusion de Pauli, qui empêche deux électrons d'occuper le même état quantique. Ce principe explique beaucoup de propriétés des électrons. Par exemple, il permet d'affirmer que des nuages d'électrons liés au même noyau occupent des orbitales toutes différentes, plutôt que de tous se concentrer dans l'orbitale la moins énergétique[118].
Classification selon le modèle standard

Dans le modèle standard de la physique des particules, les électrons appartiennent au groupe des particules subatomiques appelées « leptons »[68], que les scientifiques pensent être des particules élémentaires ou fondamentales, c'est-à-dire qu'elles ne comportent pas de sous-particules. Les électrons ont la plus faible masse de toutes les particules chargées, et appartiennent à la première famille ou génération[122]. Ils sont soumis aux forces gravitationnelles, faibles et électromagnétiques, mais échappent aux interactions fortes[123].
Les seconde et troisième générations contiennent des leptons chargés, le muon et le tauon, identiques à l'électron sous tous rapports, sauf leur masse, bien plus élevée. Les leptons diffèrent des autres constituants de base de la matière, les quarks, parce qu'ils ne sont pas sensibles aux interactions fortes. Tous les membres du groupe des leptons sont des fermions, parce qu'ils ont un spin 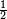 [97].
[97].
Particules virtuelles
Les physiciens pensent que le vide peut être rempli de paires de particules « virtuelles », comme des électrons et des positrons, qui se créent et s'annihilent rapidement ensuite[124]. La combinaison de la variation d'énergie nécessaire à la création de ces particules, et du temps pendant lequel elles existent, reste en dessous du seuil de détectabilité exprimé par le principe d'incertitude de Heisenberg :
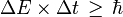 .
.
Pratiquement, l'énergie demandée pour créer les particules, 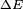 , peut être « empruntée » au vide pour une durée
, peut être « empruntée » au vide pour une durée 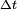 , dans la mesure où le produit n'est pas plus grand que la constante de Planck réduite
, dans la mesure où le produit n'est pas plus grand que la constante de Planck réduite 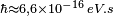 [125]. Donc pour une paire électron-positron virtuelle,
[125]. Donc pour une paire électron-positron virtuelle, 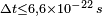 [126].
[126].
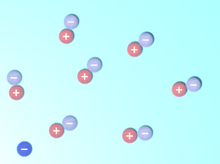
Tant qu'une paire virtuelle électron-positron subsiste, la force coulombienne du champ électrique ambiant entourant un électron fait que le positron est attiré par ce dernier, tandis que l'électron de la paire est repoussé. Ceci provoque ce que l'on appelle la « polarisation du vide »[note 11]. En fait, le vide se comporte comme un milieu ayant une permittivité diélectrique supérieure à l'unité. Donc la charge effective d'un électron est plus faible que sa valeur nominale[128]. Elle est de plus en plus élevée en s'approchant de la particule : les charges portées par les particules virtuelles masquent celle de l'électron[129],[130],[131]. Les particules virtuelles provoquent un effet de masquage comparable pour la masse de l'électron[132].
L'interaction avec des particules virtuelles explique aussi la légère déviation (environ 0,1 %) entre le moment magnétique intrinsèque de l'électron et le magnéton de Bohr (le moment magnétique anomal)[113],[133]. La précision extraordinaire de l'accord entre cette différence prévue par la théorie et la valeur déterminée par l'expérience est considérée comme une des grandes réussites de l'électrodynamique quantique[134].
En physique classique, le moment angulaire et le moment magnétique d'un objet dépendent de ses dimensions physiques. Il paraît donc incohérent de concevoir un électron sans dimensions possédant ces propriétés. Le paradoxe apparent peut être expliqué par la formation de photons virtuels dans le champ électrique engendré par l'électron. Ces photons font se déplacer l'électron de façon saccadée (ce qui s'appelle Zitterbewegung en allemand, ou mouvement de tremblement)[135] qui résulte en un mouvement circulaire avec une précession. Ce mouvement produit à la fois le spin et le moment magnétique de l'électron[68],[136]. Dans les atomes, cette création de photons virtuels explique le décalage de Lamb observé dans les raies spectrales[129].
Interaction
Champs électrique et magnétique
Un électron engendre un champ électrique qui exerce une force attractive sur une particule positivement chargée, comme un proton, et une force répulsive sur une particule négative. La valeur de cette force est donnée par la loi de Coulomb[137]. Quand un électron est en mouvement, il engendre aussi un champ magnétique[138], cause du magnétisme[139]. La loi d'Ampère-Maxwell relie le champ magnétique au mouvement d'ensemble des électrons (le courant électrique) par rapport à un observateur. C'est cette propriété d'induction qui fournit l'induction électromagnétique qui fait tourner un moteur électrique[140]. Le champ électromagnétique d'une particule chargée animée d'un mouvement arbitraire est exprimé par les potentiels de Liénard-Wiechert, valables même quand la vitesse de la particule s'approche de celle de la lumière (relativiste)[141].

Quand un électron se déplace dans un champ magnétique, il est soumis à une force de Lorentz, dirigée perpendiculairement au plan défini par le champ et la vitesse de l'électron. Cette force perpendiculaire à la trajectoire contraint l'électron, dans un champ magnétique uniforme, à suivre une trajectoire hélicoïdale dans le champ, sur un cylindre (imaginaire) dont le rayon est appelé « rayon de Larmor ». L'accélération due à ce mouvement en courbe conduit l'électron à émettre de l'énergie sous forme de rayonnement synchrotron[142],[143],[note 12]. L'émission d'énergie à son tour provoque un recul de l'électron, ce qui est connu sous le nom de « force d'Abraham-Lorentz-Dirac », qui crée une friction qui ralentit l'électron. Cette force est provoquée par une réaction du propre champ de l'électron[144].
Interaction électromagnétique
En électrodynamique quantique, l'interaction électromagnétique entre particules est transmise par des photons. Un électron isolé, qui ne subit pas d'accélération, ne peut pas émettre ni absorber un photon réel : ceci violerait la conservation de l'énergie et de la quantité de mouvement. En revanche, des photons virtuels peuvent transférer de la quantité de mouvement entre deux particules chargées. C'est cet échange de photons virtuels qui, en particulier, engendre la force de Coulomb[145]. Une émission d'énergie peut avoir lieu quand un électron en mouvement est défléchi par une particule chargée, comme un proton. L'accélération de l'électron résulte en émission de rayonnement continu de freinage[146].
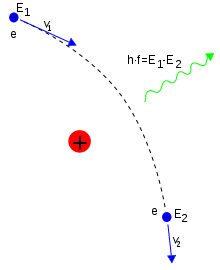
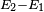 détermine la fréquence f du photon émis.
détermine la fréquence f du photon émis.Une collision inélastique entre un photon (lumière) et un électron solitaire (libre) s'appelle « diffusion Compton ». Cette collision résulte en un transfert d'énergie et de moment entre les particules, qui modifie la longueur d'onde du photon par une quantité appelée « décalage Compton »[note 13]. La valeur maximale de ce décalage est 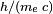 (avec
(avec  , la constante de Planck,
, la constante de Planck, 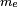 , la masse de l'électron et
, la masse de l'électron et  , la vitesse de la lumière), que l'on désigne sous le nom de « longueur d'onde de Compton »[148]. Pour un électron, elle vaut 2,43×10-12 m[2]. Une telle interaction entre la lumière et les électrons libres est appelée « diffusion Thomson » ou « diffusion linéaire de Thomson »[149].
, la vitesse de la lumière), que l'on désigne sous le nom de « longueur d'onde de Compton »[148]. Pour un électron, elle vaut 2,43×10-12 m[2]. Une telle interaction entre la lumière et les électrons libres est appelée « diffusion Thomson » ou « diffusion linéaire de Thomson »[149].
La force relative de l'interaction électromagnétique entre deux particules, comme un électron et un proton, est donnée par la constante de structure fine. C'est une quantité sans dimension formée par le rapport de deux énergies : l'énergie électrostatique d'attraction (ou de répulsion) à la distance d'une longueur d'onde de Compton, et l'énergie au repos de la charge. La constante est donnée par α ≈ 7,297353×10-3, qui vaut approximativement 1/137[2].
Quand des électrons et des positrons entrent en collision, ils peuvent s'annihiler, donnant 2 ou 3 photons. Si l'électron et le positron ont un moment négligeable, il peut se former un état lié (positronium) avant que l'annihilation ne se produise, donnant 2 ou 3 photons, dont l'énergie totale est 1,022 MeV[150],[151]. Par ailleurs, des photons de haute énergie peuvent se transformer en une paire d'électron et positron par un processus inverse de l'annihilation que l'on appelle « production de paires », mais seulement en présence d'une particule chargée proche, comme un noyau, susceptible d'absorber le moment de recul[152],[153].
En théorie des interactions électrofaibles, la composante gauche de la fonction d'onde de l'électron forme un doublet d'isospin faible avec le neutrino-électron. Vis-à-vis des interactions faibles, les neutrinos-électrons se comportent en effet comme des électrons. Chaque membre de ce doublet peut subir une interaction par courant chargé transformant l'un en l'autre par émission ou absorption de boson W±, cette transformation étant à la base de la désintégration β des noyaux. L'électron, comme le neutrino, peut subir une interaction par courant neutre couplé au Z0, ce qui est notamment la cause de la diffusion électron-neutrino[154]. En plus de l'isopsin, l'électron est doté d'une hypercharge selon la théorie électrofaible[155].
Atomes et molécules
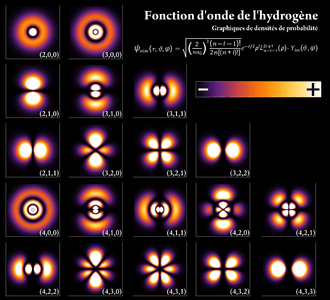

Un électron peut être « lié » au noyau d'un atome par la force de Coulomb attractive[156]. Un système d'électrons liés à un noyau en nombre égal à la charge positive de ce dernier est appelé un « atome neutre »[157]. Si le nombre d'électrons est différent, le système s'appelle un « ion »[158]. Le noyau des atomes comporte des protons et, en général, des neutrons. Les atomes sont donc formés de trois particules : électrons, neutrons et protons[159],[160]. Le comportement ondulatoire d'un électron lié est décrit par une fonction appelée « orbitale atomique ». Chaque orbitale a son propre ensemble de nombres quantiques, tels que l'énergie, le moment angulaire et la projection de ce dernier sur un axe donné[161]. Suivant le principe d'exclusion de Pauli, chaque orbitale ne peut être occupée au plus que par deux électrons, de spins différents[162].
Les électrons peuvent changer d'orbitale par émission ou absorption d'un photon dont l'énergie égale la différence d'énergie potentielle entre ces orbitales atomiques[163]. D'autres méthodes de transfert d'orbitale comprennent les collisions avec des particules comme les électrons, et l'effet Auger[164]. Pour s'échapper d'un atome, l'énergie de l'électron doit être hissée au-dessus de son énergie de liaison à l'atome. Ceci peut arriver dans l'effet photoélectrique, quand un photon incident a une énergie qui dépasse l'énergie d'ionisation de l'électron qui l'absorbe[165].
Le moment angulaire orbital des électrons est quantifié. Comme l'électron est chargé, il produit un moment magnétique orbital proportionnel à son moment angulaire. Le moment magnétique total d'un atome est égal à la somme des moments magnétiques propres et orbitaux de tous les électrons et du noyau. Celui du noyau, cependant, est négligeable par rapport à celui des électrons. Les moments magnétiques des électrons qui occupent la même orbitale (électrons en paire) s'annulent[166].
En physique, la liaison chimique entre atomes résulte d'interactions électromagnétiques, décrites par les lois de la mécanique quantique[167]. Selon leur proximité du noyau, les chimistes considèrent les électrons de cœur et les électrons de valence ; ce sont ces derniers qui interviennent dans la liaison chimique[168]. Les plus fortes sont les liaisons covalentes et les liaisons ioniques, qui permettent la formation de molécules[169]. Dans une molécule, les électrons se déplacent sous l'influence de plusieurs noyaux, et occupent des orbitales moléculaires, de la même façon qu'ils occupent des orbitales dans des atomes isolés[170]. Un facteur fondamental dans ces structures moléculaires est l'existence de paires d'électrons : celles-ci sont des électrons de spins opposés, ce qui leur permet d'occuper la même orbitale moléculaire sans violer le principe d'exclusion de Pauli (de la même manière que dans les atomes). Les orbitales moléculaires différentes ont des distributions spatiales de densité d'électrons différentes. Par exemple, dans les paires liantes — qui lient les atomes ensemble, on trouve des électrons avec une densité maximale dans un relativement petit volume entre les atomes. Au contraire, pour les paires non liantes, les électrons sont distribués dans un grand volume autour des noyaux[171]. C'est l'existence de paires liantes, où des électrons périphériques sont mis en commun par deux atomes voisins, qui caractérise la liaison covalente. La liaison ionique s'établit lorsque deux ions sont fortement liés par attraction électrostatique[172], ce qui se produit si un électron d'un atome a une orbitale moléculaire majoritairement située à proximité de l'autre atome.
Les réactions d'oxydoréduction — des échanges d'électrons — englobent la combustion, la métallurgie, l'électrochimie, la corrosion et la respiration cellulaire[173],[174].
Conductivité électrique

Si un corps a trop d'électrons, ou pas assez, pour équilibrer les charges positives des noyaux, il a une charge électrique non nulle : négative s'il y a trop d'électrons ; positive dans le cas contraire. Si les charges s'équilibrent, le corps est dit neutre[178].
Des électrons se déplaçant indépendamment, comme dans le vide, sont dits « libres ». Les électrons de valence dans les métaux se comportent aussi comme s'ils étaient libres. De plus, il peut y avoir dans un solide des trous, qui sont des endroits où manque un électron. Ces trous peuvent être comblés par les électrons voisins, mais cela ne fera que déplacer les trous. On peut avoir dans des solides une prédominance de la conduction de l'électricité par le déplacement de trous, plutôt que par le déplacement d'électrons. En fait les particules porteuses de charge dans les métaux et autres solides sont des « quasi-particules », de charge électrique négative ou positive, semblables aux électrons réels[179].
Quand les électrons libres se déplacent — que ce soit dans le vide ou dans un métal, ils produisent un courant de charges net, que l'on appelle courant électrique, qui engendre un champ magnétique. De même, un courant peut être engendré par un champ électrique, éventuellement provoqué par un champ magnétique variable (induction électromagnétique). Ces interactions sont décrites mathématiquement par les équations de Maxwell[180].
À une température donnée, chaque matériau a une conductivité électrique qui détermine la valeur du courant électrique quand un potentiel électrique est appliqué. Des exemples de bons conducteurs comprennent des métaux comme le cuivre et l'or, tandis que le verre et le Teflon sont de mauvais conducteurs (ce sont des isolants). Dans tout matériau diélectrique, les électrons restent liés à leurs atomes respectifs, et le matériau se comporte comme un isolant électrique. La plupart des semi-conducteurs ont un degré de conductivité variable entre les extrêmes du conducteur et de l'isolant[181]. Par ailleurs, les métaux ont une structure en bandes électroniques dont certaines ne sont que partiellement remplies. La présence de ce type de bandes permet aux électrons de se comporter comme s'ils étaient libres ou délocalisés. Quand un champ électrique est appliqué, ils peuvent se déplacer comme les molécules d'un gaz (appelé « gaz de Fermi »)[182] à travers la matière, un peu comme des électrons libres. Ces phénomènes sont à la base de toute l'électricité : électrocinétique, électronique et radioélectricité.
En raison des collisions entre électrons et atomes, la vitesse de dérive des électrons dans un conducteur est de l'ordre du mm/s. Cependant la vitesse à laquelle un changement de courant en un point de la matière se répercute sur les courants en d'autres points, la célérité, est typiquement 75 % de la vitesse de la lumière dans le vide[183]. Ceci se produit parce que les signaux électriques se propagent comme une onde, avec une vitesse qui ne dépend que de la constante diélectrique, ou permittivité[184], du milieu.
Les métaux sont de relativement bons conducteurs de la chaleur, avant tout parce que les électrons délocalisés peuvent transporter de l'énergie thermique d'un atome à l'autre. Cependant, contrairement à la conductivité électrique, la conductivité thermique d'un métal est pratiquement indépendante de la température. Ceci s'exprime mathématiquement par la loi de Wiedemann et Franz[182], qui dit que le rapport de la conductivité thermique à la conductivité électrique est proportionnel à la température. Comme le désordre thermique du réseau du métal accroît la résistivité du milieu, cela conduit le courant électrique à dépendre de la température[185].
Quand on les refroidit en dessous d'une température critique, les substances peuvent subir une transition de phase qui leur fait perdre toute résistivité au courant électrique, phénomène appelé « supraconductivité ». Dans la théorie BCS, ce comportement est expliqué par des paires d'électrons (formant des bosons) qui entrent dans l'état connu sous le nom de « condensat de Bose-Einstein ». Ces paires de Cooper voient leur mouvement couplé à la matière environnante par des vibrations du réseau nommées « phonons », évitant ainsi les collisions avec les atomes responsables de la résistance électrique[186],[187],[188],[189].
Dans les conducteurs solides, les électrons sont des quasi-particules. Quand ils sont fortement confinés aux températures proches du zéro absolu, ils se comportent comme s'ils se décomposaient en deux autres quasi-particules, des spinons et des chargeons[190],[191]. La première transporte le spin et le moment magnétique ; la seconde, la charge électrique : c'est la séparation spin-charge.
Interaction de la lumière et des électrons
« Je veux [...] vous parler du domaine de la physique le mieux connu, à savoir l'interaction de la lumière et des électrons. La plupart des phénomènes qui vous sont familiers mettent en jeu cette interaction de la lumière et des électrons — c'est le cas, par exemple, de l'ensemble des phénomènes physiques traités par la chimie et la biologie. Seuls les phénomènes de gravitation et les processus nucléaires échappent à cette théorie [...] »
— Richard Feynman[192]

L'incandescence, qui apparaît dans les matériaux chauffés[193], est provoquée par les changements d'orbitales des électrons dans l'atome. La luminescence est une émission de lumière qui survient à de relativement basses températures[194] et est aussi une conséquence des changements d'orbitales des électrons dans l'atome. Quand un électron est accéléré, il peut rayonner de l'énergie sous forme de photons[195],[196]. Ce rayonnement électromagnétique se manifeste sous la forme d'ondes radio, de micro-ondes, d'infrarouges, de lumière visible (perçue par l'œil humain[197]), d'ultraviolets, de rayons X ou de rayons gamma.
La diffusion optique, une interaction entre la lumière et les électrons, explique la réflexion optique[198]. La diffusion Rayleigh permet d'expliquer la couleur du ciel[199] et la couleur des plumes de certains oiseaux[200]. La réfraction des ondes électromagnétiques est aussi issue de l'interaction de la lumière et des électrons[201]. Ces phénomènes optiques sont aussi causés par l'interaction des photons avec d'autres particules chargées tel le proton[202]. La plupart des interactions des photons avec la matière se ramènent à trois phénomènes : effet photoélectrique, diffusion Compton et production de paires électron-positron (ou matérialisation)[203],[204]. Ils se manifestent la plupart du temps en présence d'électrons, car ce sont les particules chargées les moins lourdes[205],[206].
Mouvement et énergie
Selon la relativité restreinte d'Albert Einstein, quand la vitesse d'un électron se rapproche de la vitesse de la lumière, du point de vue d'un observateur, sa masse relativiste augmente, ce qui rend de plus en plus difficile de l'accélérer à partir du repère de l'observateur. Ainsi, la vitesse d'un électron peut s'approcher de la vitesse de la lumière dans le vide c, mais jamais l'atteindre. Si un électron relativiste, c'est-à-dire se déplaçant à une vitesse proche de c, est injecté dans un milieu diélectrique comme l'eau, où la vitesse de la lumière est significativement inférieure à c, il va se déplacer plus vite que la lumière dans le milieu. Le déplacement de sa charge dans le milieu va produire une légère lumière appelée « rayonnement Tcherenkov »[207],[208],[209] par effet Vavilov-Tcherenkov.
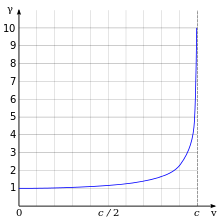
Les effets de la relativité restreinte sont basés sur une quantité appelée facteur de Lorentz[210], défini comme
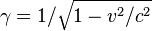 ,
,
où v est la vitesse de la particule. L'énergie cinétique  d'un électron se déplaçant à la vitesse v est :
d'un électron se déplaçant à la vitesse v est :
où 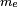 est la masse de l'électron[211]. À titre d'exemple, l'accélérateur linéaire de SLAC peut accélérer un électron jusqu'à environ 51 GeV[212]. Puisque la masse de l'électron est de 0,51 MeV/c2, ceci donne une valeur d'environ 100 000 pour
est la masse de l'électron[211]. À titre d'exemple, l'accélérateur linéaire de SLAC peut accélérer un électron jusqu'à environ 51 GeV[212]. Puisque la masse de l'électron est de 0,51 MeV/c2, ceci donne une valeur d'environ 100 000 pour  . Le moment relativiste d'un tel électron est donc 100 000 fois celui que la mécanique classique prédirait à un électron de cette vitesse[note 14].
. Le moment relativiste d'un tel électron est donc 100 000 fois celui que la mécanique classique prédirait à un électron de cette vitesse[note 14].
Comme un électron se comporte également comme une onde, à une vitesse donnée, il a une longueur d'onde de De Broglie caractéristique donnée par
où h est la constante de Planck et p la quantité de mouvement[213],[73].
Destruction et création
Les électrons sont détruits lors de la capture électronique qui survient dans les noyaux d'atomes radioactifs. En 1937, étudiant les réactions nucléaires dans le vanadium 49, le physicien américain Luis Walter Alvarez observe le premier des captures électroniques[214],[215].
La plupart des électrons de l'Univers ont été créés lors du Big Bang[216],[217]. Ils peuvent être aussi produits par radioactivité β des noyaux radioactifs[218] et dans des collisions de haute énergie telles celles engendrées par la pénétration de rayons cosmiques dans l'atmosphère terrestre[219],[220]. Il existe trois processus de création d'électrons.
À la naissance de l'Univers
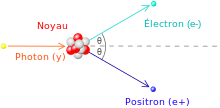
Le Big Bang est la théorie scientifique la plus largement acceptée pour expliquer les premiers stades de l'évolution de l'Univers[221], dont l'âge est estimé en 2011 à environ 13,75 milliards d'années[222]. Pendant la première milliseconde après le Big Bang, les températures atteignent 107 K, et les photons ont une énergie moyenne supérieure à 1 MeV. Ils ont donc des énergies suffisantes pour réagir ensemble et former des paires d'électron-positron :
où γ est un photon, e+ un positron et e- un électron. Inversement, des paires électron-positron s'annihilent pour émettre des photons énergétiques. Il y a donc pendant cette période un équilibre entre électrons, positrons et photons. Au bout de 15 secondes, la température de l'Univers est descendue sous la valeur où la création de paires positron-électron peut avoir lieu. La plupart des électrons et des positrons qui restent s'annihilent, relâchant des photons qui réchauffent l'univers pour un temps[223].
Pour des raisons encore inconnues de nos jours, pendant le processus de leptogénèse, il y a en fin de compte plus d'électrons que de positrons[224]. Il en résulte qu'un électron sur environ un milliard a survécu au processus d'annihilation. Cet excès a compensé l'excès des protons sur les antiprotons, dans le processus appelé « baryogénèse », ce qui résulte en une charge nette nulle pour l'Univers[225],[226]. Les protons et neutrons qui ont survécu ont commencé à réagir ensemble, dans un processus appelé nucléosynthèse primordiale, formant des isotopes de l'hydrogène et de l'hélium, ainsi qu'un tout petit peu de lithium. Ce processus a culminé au bout de 5 minutes[227]. Tous les neutrons résiduels ont subi une désintégration β, avec une vie moyenne de mille secondes, relâchant un proton, un électron et un antineutrino, par le processus :
où n est un neutron, p un proton et 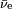 un antineutrino électronique. Pour la période allant jusqu'à 300 000-400 000 ans, les électrons restants sont trop énergétiques pour se lier aux noyaux atomiques[228], et toute la lumière circulant dans l'Univers est constamment diffusée par ces électrons. Il suit une période que l'on appelle la « recombinaison », où les atomes neutres sont formés, et l'univers en expansion devient transparent au rayonnement[229].
un antineutrino électronique. Pour la période allant jusqu'à 300 000-400 000 ans, les électrons restants sont trop énergétiques pour se lier aux noyaux atomiques[228], et toute la lumière circulant dans l'Univers est constamment diffusée par ces électrons. Il suit une période que l'on appelle la « recombinaison », où les atomes neutres sont formés, et l'univers en expansion devient transparent au rayonnement[229].
Dans les étoiles

Environ un million d'années après le Big Bang, la première génération d'étoiles commence à se former[229]. Dans une étoile, la nucléosynthèse stellaire aboutit à la production de positrons par fusion de noyaux atomiques et désintégration β+ des noyaux ainsi produits, qui transforme l'excès de protons en neutrons. Les positrons ainsi produits s'annihilent immédiatement avec les électrons, en produisant des rayons gamma. Le résultat net est une réduction constante du nombre d'électrons, et la conservation de la charge par un nombre égal de transformations de protons en neutrons. Cependant, le processus d'évolution stellaire peut aboutir à la synthèse de noyaux lourds instables, qui à leur tour peuvent subir des désintégrations β-, ce qui recrée de nouveaux électrons[230]. Un exemple en est le nucléide cobalt 60 (60Co), qui se désintègre en nickel 60 (60Ni)[231].
Au bout de sa vie, une étoile plus lourde que 20 masses solaires peut subir un effondrement gravitationnel pour former un trou noir[232]. Selon la physique classique, ces objets stellaires massifs exercent une attraction gravitationnelle suffisamment forte pour empêcher tout objet, y compris le rayonnement électromagnétique, de s'échapper du rayon de Schwarzschild[233]. Cependant des astrophysiciens pensent que les effets quantiques permettent au trou noir d'émettre un faible rayonnement de Hawking à cette distance et que des électrons (et des positrons) sont créés à l'horizon des trous noirs[234].
Quand des paires de particules virtuelles — comme un électron et un positron — sont créées au voisinage de l'horizon, leur distribution spatiale aléatoire peut permettre à l'une d'entre elles d'apparaître à l'extérieur : ce processus est nommé effet tunnel quantique. Le potentiel gravitationnel du trou noir peut alors fournir l'énergie qui transforme cette particule virtuelle en une particule réelle, ce qui lui permet de se répandre dans l'espace[235]. En échange, l'autre membre de la paire reçoit une énergie négative, ce qui résulte en une perte nette de masse-énergie du trou noir. Le rythme du rayonnement de Hawking croît quand la masse décroît, ce qui finit par provoquer l'évaporation complète du trou noir[236].
Par les rayons cosmiques
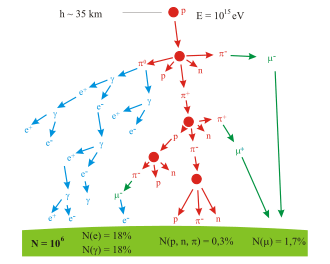
Les rayons cosmiques sont des particules se déplaçant dans l'espace avec de très grandes énergies. Des événements avec des énergies jusqu'à 3×1020 eV ont été observés[237]. Quand ces particules rencontrent des nucléons dans l'atmosphère terrestre, elles engendrent une gerbe de particules, comprenant des pions[238]. Plus de la moitié du rayonnement cosmique observé au niveau du sol consiste en muons. Le muon est un lepton produit dans la haute atmosphère par la désintégration d'un pion[239]. À son tour, le muon va se désintégrer pour former un électron ou un positron. Donc, pour le pion négatif π-,
où 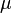 est un muon et
est un muon et  un neutrino muonique.
un neutrino muonique.
Observation

L'observation à distance des électrons exige la détection de l'énergie qu'ils rayonnent. Par exemple, dans des environnements riches en phénomènes énergétiques comme la couronne des étoiles, les électrons libres forment un plasma et transmettent de l'énergie par rayonnement continu de freinage. Le gaz d'électrons peut subir une onde de plasma, qui consiste en ondes provoquées par des variations synchronisées de la densité d'électrons, ce qui provoque des émissions d'énergie détectables avec des radiotélescopes[241].
Dans les conditions de laboratoire, les interactions d'un électron peuvent être observées au moyen de détecteurs de particules, ce qui permet la mesure des propriétés spécifiques telles que l'énergie, le spin ou la charge[165]. La mise au point des pièges de Paul et de Penning permet de contenir des particules chargées dans un petit volume pour de grandes durées. Ceci permet des mesures précises des propriétés des particules[242],[note 15].
Les premières images de la distribution en énergie d'un électron ont été réalisées par un groupe de l'université de Lund en Suède, en février 2008. Les scientifiques ont utilisé des impulsions très brèves de lumière (de 1 attoseconde, soit 10-18 s), qui ont permis pour la première fois d'observer le mouvement de l'électron[244],[245].
La distribution des électrons dans les solides peut être visualisée par spectrométrie photoélectronique UV analysée en angle. Cette technique utilise l'effet photoélectrique pour mesurer le réseau réciproque — représentation mathématique des structures périodiques utilisée pour déduire la structure originelle. L'ARPES peut être utilisée pour déterminer la direction, la vitesse et la diffusion des électrons au sein du solide[246].
Applications
Les propriétés de l'électron sont exploitées dans le microscope électronique[247], le tube cathodique[248], le soudage[249], l'effet laser[250], le capteur photographique[251] et l'accélérateur de particules[252].
Expressions
- Électron anti-liant : électron occupant une orbitale moléculaire antiliante[253] ;
- Électrons appariés : électrons de spin opposés occupant une même orbitale atomique ou moléculaire[253] ;
- Électron Auger : électron émis par effet Auger[254] ;
- Électron célibataire : qui occupe seul une orbitale atomique ou moléculaire[253] ;
- Électron de conduction : situé dans la bande de conduction d'un solide[253] ;
- Électrons équivalents : électrons d'un atome ayant les mêmes nombres quantiques n et l, ils occupent donc la même sous-couche[253] ;
- Électron K, L… : qui appartient à la couche K, L, etc.[253] ;
- Électron liant : occupe une orbitale liante d'une molécule et participe donc à la liaison chimique[253] ;
- Électron libre : électron faiblement attaché au noyau d'un atome[254]. Également, de façon imagée, se dit d'une personne agissant selon ses valeurs, en dehors des normes établies par une institution[7].
- Électron optique : présent dans la couche non saturée la plus externe de l'atome, il intervient dans les liaisons chimiques[253] ;
- Électron périphérique : synonyme d'électron de valence[255] ;
- Électron secondaire : électron émis par un solide frappé par des électrons[253] ;
- Électron de valence : présent dans la couche non saturée la plus externe de l'atome, il émet des rayonnements électromagnétiques qui sont étudiés en spectroscopie atomique[253] ;
- Électron-volt : unité de mesure de l'énergie surtout utilisée en physique des particules[253] ;
- Rayon classique de l'électron : si l'électron est considéré comme une sphère, son rayon théorique tel que calculé selon la mécanique quantique[256] ;
- Rayon de l'électron : rayon théorique de l'électron[256] ;
- Théorie des électrons de Lorentz : proposée par Hendrik Lorentz vers la fin du XIXe siècle[253],[257].
D'autres expressions, tels « modèle de l'électron libre[258] » et « gaz d'électrons[259] », comprennent le mot « électron ».
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Electron » (voir la liste des auteurs).
Notes
- ↑ Selon CODATA 2006, elle est plus précisément de 9,109 382 6(16)×10-31 kg. Selon CODATA 2010, elle est de 9,109 382 91(40)×10-31 kg[2]. Selon Augustin 2008, elle est de 9,109 389 7(54)×10-31 kg[37].
- ↑ Selon CODATA 2006, elle est plus précisément de 510,998 918(44) keV. Selon CODATA 2010, elle est de 510,998 928(11) keV[2]. Selon Augustin 2008, elle est de 510,999 06(15) keV[37].
- ↑ Selon CODATA 2006, le rapport est plus précisément de 1 836,152 672 45(75)[92].
- ↑ Selon CODATA 2006, elle est plus précisément de −1,602 176 53(14)×10-19 C. Selon CODATA 2010, elle est de −1,602 176 565(35)×10-19 C[2].
- ↑ En théorie des supercordes, l'électron n'est pas ponctuel car il n'existe « qu'un seul constituant élémentaire : une toute petite corde unidimensionnelle[trad 1] »[103].
- ↑ Cette valeur numérique s'obtient ainsi :
 et
et 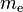 sont la charge électrique et la masse de l'électron,
sont la charge électrique et la masse de l'électron,  est la vitesse de la lumière dans le vide et
est la vitesse de la lumière dans le vide et 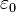 est la permittivité du vide[105].
est la permittivité du vide[105]. -
- ↑ Le rayon classique de l'électron intervient de la façon suivante : supposons que la charge de l'électron soit distribuée uniformément dans un volume sphérique. Puisque les parties du volume se repoussent, la sphère contient une énergie potentielle électrostatique. Supposons que cette énergie est égale à l'énergie au repos E définie par la relation relativiste
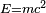 , où m est la masse au repos et c la vitesse de la lumière dans le vide. En électrostatique, l'énergie potentielle d'une sphère de rayon r et de charge e est donnée par :
, où m est la masse au repos et c la vitesse de la lumière dans le vide. En électrostatique, l'énergie potentielle d'une sphère de rayon r et de charge e est donnée par : 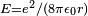 , où ε0 est la permittivité du vide. En égalant ces deux valeurs, on obtient la valeur de r citée[107].
, où ε0 est la permittivité du vide. En égalant ces deux valeurs, on obtient la valeur de r citée[107]. - ↑ Cette valeur
 s'obtient à partir de la valeur du spin
s'obtient à partir de la valeur du spin 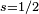 par[112] :
par[112] :
- ↑ Le magnéton de Bohr se calcule par :
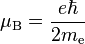 ,
,
 la charge élémentaire,
la charge élémentaire, 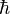 la constante de Planck réduite et
la constante de Planck réduite et 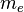 la masse de l'électron.
la masse de l'électron. - ↑ Elle est plus précisément de 9,274 009 15(23)×10-24 J/T[2].
- ↑ Cette polarisation a été confirmée expérimentalement en 1997 en utilisant l'accélérateur de particules japonais TRISTAN[127].
- ↑ Le rayonnement émis par des électrons non relativistes est parfois nommé « rayonnement cyclotron ».
- ↑ Le changement de longueur d'onde
 dépend de l'angle de recul
dépend de l'angle de recul 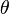 de la façon suivante :
de la façon suivante :
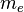 la masse de l'électron et c est la vitesse de la lumière dans le vide[147].
la masse de l'électron et c est la vitesse de la lumière dans le vide[147]. -
- ↑ La vitesse de l'électron étant voisine de c, la mécanique classique donnerait un moment mc, alors que la mécanique relativiste donne
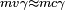 , d'où un facteur de 100 000.
, d'où un facteur de 100 000. - ↑ Le moment magnétique de l'électron a été mesuré avec une précision de 11 chiffres significatifs, ce qui, en 1980, était une précision supérieure à la mesure de toute autre constante physique[243].
Citations originales
- ↑ (en) « there is only one elementary constituent: a tiny, one-dimensional "string," »
- ↑ (en) « The state in which a heated body, naturally incapable of emitting light, becomes luminous, is called a state of incandescence. »
Références
- ↑ Pour plus de détails, consulter par exemple Dahl 1997, p. 72.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Les données sont publiées dans un portail du National Institute of Standards and Technology (NIST) et sont accessibles via un moteur de recherche ou en cliquant sur des boutons : (en) « The NIST Reference on Constants, Units and Uncertainty », National Institute of Standards and Technology, (consulté le 22 février 2010). Ces données sont appelées CODATA. La source originale des données CODATA est Mohr, Taylor et Newell 2006.
- ↑ (en) Le Roy C. Cooley, Natural Philosophy for Common and High Schools, New York, Éditions Scribner, , p. 159, fig. 82
- ↑ (en) Joseph T. Shipley, Dictionary of Word Origins, The Philosophical Library, , p. 133
- ↑ Rosmorduc 1985, p. 119
- ↑ (en) Brian Baigrie, Electricity and Magnetism : A Historical Perspective, Greenwood Press, (ISBN 0-313-33358-0, résumé), p. 7–8
- 1 2 Josette Rey-Debove (dir.) et Alain Rey (dir.), Le Nouveau Petit Robert : Dictionnaire alphabétique et analogique de la langue française, Dictionnaires Le Robert, , p. 847
- ↑ (en) Joseph F. Keithley, The Story of Electrical and Magnetic Measurements : From 500 B.C. to the 1940s, Wiley, (ISBN 0-7803-1193-0)
- ↑ (en) Eric W. Weisstein, « Benjamin Franklin (1706–1790) », Eric Weisstein's World of Scientific Biography (consulté le 14 août 2012)
- ↑ (en) « Benjamin Franklin », dans The Encyclopedia Americana; a library of universal knowledge, New York, Encyclopedia Americana Corp.,
- ↑ (en) Wilfred V. Farrar, « Richard Laming and the Coal-Gas Industry, with His Views on the Structure of Matter », Ann. Sci., Londres, Taylor & Francis, vol. 25, , p. 243–254 (ISSN 0003-3790, DOI 10.1080/00033796900200141)
- ↑ (en) Daniel M. Siegel, Innovation in Maxwell's Electromagnetic Theory : Molecular vortices, displacement current, and light, Cambridge, Cambridge University Press, (ISBN 978-0521533294, lire en ligne), p. 10-11
- ↑ (en) John D. Barrow, « Natural Units Before Planck », Quarterly Journal of the Royal Astronomical Society, vol. 24, , p. 24–26
- ↑ Buchwald et Warwick 2001, p. 195-203
- ↑ (en) Theodore Arabatzis, Representing Electrons : A Biographical Approach to Theoretical Entities, University of Chicago Press, (ISBN 0-226-02421-0, lire en ligne), p. 70–74
- ↑ (en) George Johnstone Stoney, « Of the "Electron," or Atom of Electricity », Philosophical Magazine, vol. 38, no 5, , p. 418–420
- ↑ (en) Anne H. Soukhanov (dir.), Word Mysteries & Histories, Houghton Mifflin Company, (ISBN 0-395-40265-4), p. 73
- ↑ (en) David B. Guralnik (dir.), Webster's New World Dictionary, Prentice Hall, , p. 450
- ↑ Par exemple, les deux ont rapporté leurs observations sur les spectres lumineux dans (en) Dr. J. Plücker et Dr. J. W. Hittorf, « On the Spectra of Ignited Gases and Vapours, with especial regard to the different Spectra of the same elementary gaseous substance », Philosophical Transactions, , p. 3-4 (lire en ligne [PDF]) Le fichier pèse 17 Mo et l'article comprend 53 pages.
- ↑ (en) Å. G. Ekstrand, « The Nobel Prize in Physics 1919 - Presentation Speech », Fondation Nobel, (consulté le 14 août 2012) : « As long ago as 1869 Hittorf discovered that if a low pressure is set up in a discharge tube, rays are emitted from the negative electrode, the so-called cathode. »
- ↑ (en) Wolfgang Demtröder, Atoms, Molecules and Photons : An Introduction to Atomic-, Molecular- and Quantum Physics, Springer, , 573 p. (ISBN 978-3540206316), p. 34
- ↑ Dahl 1997, p. 55-58
- ↑ (en) Robert DeKosky, « William Crookes and the quest for absolute vacuum in the 1870s », Ann. Sci., Taylor & Francis, vol. 40, no 1, , p. 1–18 (DOI 10.1080/00033798300200101)
- 1 2 3 (en) Henry M. Leicester, The Historical Background of Chemistry, Dover Publications, (ISBN 0-486-61053-5), p. 221–222
- ↑ Dahl 1997, p. 64-78
- ↑ (en) Pieter Zeeman et Norman Lockyer (dir.), « Sir William Crookes, F.R.S. », Nature, Nature Publishing Group, vol. 77, no 1984, , p. 1–3 (DOI 10.1038/077001a010.1038/077001a0, lire en ligne)
- ↑ Dahl 1997, p. 99
- ↑ Micheline Charpentier-Morize, Perrin savant et homme politique, Paris, Belin, , 285 p. (ISBN 978-2701120027, présentation en ligne), p. 25-28
- ↑ Rosmorduc 1985, p. 205
- 1 2 Dahl 1997, p. 122-185
- ↑ (en) J. J. Thomson, « Cathode Rays », Phil. Mag., vol. 44, no 293, (lire en ligne [PDF])
- ↑ (en) Robert Wilson, Astronomy Through the Ages : The Story of the Human Attempt to Understand the Universe, CRC Press, (ISBN 0-7484-0748-0), p. 138
- ↑ (en) Joseph J. Thomson, Carriers of Negative Electricity : Nobel Lecture, December 11, 1906, Oslo (Suède), Fondation Nobel, (lire en ligne [PDF]), p. 9
- ↑ Serway 1992, p. 473
- ↑ Benoît Lelong, « Personne n'a découvert l'électron », La Recherche (consulté le 9 août 2012)
- ↑ Allan R. Glanville (dir.), Scientifica, le guide universel du monde de la science : Mathématiques, physique, astronomie, biologie, chimie, géologie, médecine, H. F. Ullmann, (ISBN 978-3-8480-0494-2), p. 148
- 1 2 3 4 Augustin 2008, p. 116.
- ↑ Pablo Jensen, Des atomes dans mon café crème : La physique peut-elle tout expliquer ?, Seuil, coll. « Points Sciences », (ISBN 978-2-02-062984-3), p. 208-211
- ↑ (en) Thaddeus J. Trenn, « Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays », Isis, vol. 67, no 1, , p. 61–75 (DOI 10.1086/351545)
- ↑ Henri Becquerel, « Déviation du rayonnement du radium dans un champ électrique », Comptes rendus hebdomadaires des séances de l'Académie des sciences, Académie des sciences, vol. 130, , p. 809–815
- ↑ Buchwald et Warwick 2001, p. 90–91
- ↑ (en) William G. Myers, « Becquerel's Discovery of Radioactivity in 1896 », Journal of Nuclear Medicine, Society of Nuclear Medicine, vol. 17, no 7, , p. 579–582 (lire en ligne [PDF])
- ↑ (en) Isaak K. Kikoin et Isaak S. Sominskiĭ, « Abram Fedorovich Ioffe (on his eightieth birthday) », Soviet Physics Uspekhi, vol. 3, , p. 798–809 (DOI 10.1070/PU1961v003n05ABEH005812). Publication originale en russe : (ru) И.К. Кикоин et М.С. Соминский, « Академик А.Ф. Иоффе », Успехи Физических Наук, vol. 72, no 10, , p. 303–321 (lire en ligne [PDF])
- ↑ (en) Robert A. Millikan, « The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes' Law », Physical Review, no 32, , p. 349–397 (DOI 10.1103/PhysRevSeriesI.32.349)
- ↑ Ilarion Pavel, « La mesure par Millikan de la charge de l'électron », BibNum, (lire en ligne) L'information apparaît sous l'onglet Analyse.
- ↑ (en) N. N. Das Gupta et Sanjay K. Ghosh, « A Report on the Wilson Cloud Chamber and Its Applications in Physics », Reviews of Modern Physics, The American Physical Society, vol. 18, , p. 225–290 (DOI 10.1103/RevModPhys.18.225)
- ↑ McFee 2012, p. 130-131, 135
- ↑ McEvoy, Zarate et Groves 2014, p. 72-75.
- ↑ (en) M. S. Longair, Theoretical Concepts in Physics : An alternative view of theoretical reasoning in physics, Cambridge University Press, (ISBN 978-0-521-52878-8, lire en ligne), p. 377–378
- ↑ Voir par exemple (en) J. Mehra et H. Rechenberg, The Historical Development of Quantum Theory, vol. 1, New York, Springer-Verlag, (ISBN 3-540-90642-8), p. 193–196
- ↑ (en) Niels Bohr, The Structure of the Atom : Nobel Lecture, December 11, 1922, Fondation Nobel, (lire en ligne [PDF]), p. 37
- ↑ C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique, t. 1, Hermann, (ISBN 2705660747), chap. 1
- 1 2 3 Smirnov 2003, p. 14–21
- ↑ McEvoy, Zarate et Groves 2014, p. 78-89, 101-104 et 119.
- ↑ (en) Gilbert N. Lewis, « The Atom and the Molecule », Journal of the American Chemical Society, vol. 38, no 4, , p. 762–786 (DOI 10.1021/ja02261a002)
- 1 2 (en) Theodore Arabatzis et Kostas Gavroglu, « The Chemists' Electron », European Journal of Physics, vol. 18, , p. 150–163 (DOI 10.1088/0143-0807/18/3/005)
- ↑ (en) Irving Langmuir, « The Arrangement of Electrons in Atoms and Molecules », Journal of the American Chemical Society, vol. 41, no 6, , p. 868–934 (DOI 10.1021/ja02227a002)
- ↑ (en) Eric R. Scerri, The Periodic Table, Oxford University Press, (ISBN 0-19-530573-6), p. 205–226
- ↑ McFee 2012, p. 132-133
- ↑ (en) Michela Massimi, Pauli's Exclusion Principle, The Origin and Validation of a Scientific Principle, Cambridge University Press, (ISBN 0-521-83911-4), p. 7–8
- ↑ (de) G. E. Uhlenbeck et S. Goudsmit, « Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons », Die Naturwissenschaften, vol. 13, no 47, , p. 953 (DOI 10.1007/BF01558878)
- ↑ (de) Wolfgang Pauli, « Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes », Zeitschrift für Physik, vol. 16, no 1, , p. 155–164 (DOI 10.1007/BF01327386)
- ↑ (en) K. A. Peacock, The Quantum Revolution : A Historical Perspective, Greenwood Publishing Group, (ISBN 0-313-33448-X, lire en ligne), p. 47
- ↑ (en) M. H. Krieger, Constitutions of Matter : Mathematically modeling the most everyday of physical phenomena, University of Chicago Press, (ISBN 0-226-45305-7, lire en ligne), p. 22
- 1 2 Augustin 2008, p. 118.
- ↑ Thorne 1997, p. 150 (note).
- ↑ McEvoy, Zarate et Groves 2014, p. 99.
- 1 2 3 4 Curtis 2003
- ↑ (de) Heinrich Hertz, « Ueber den Einfluss des ultravioletten Lichtes auf die electrische Entladung », Annalen der Physik, vol. 267, no 8, , p. 983–1000 (DOI 10.1002/andp.18872670827, Bibcode 1887AnP...267..983H)
- ↑ (en) « for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect » in Fondation Nobel, « The Nobel Prize in Physics 1921 », Fondation Nobel, 2010. Consulté le 15 juin 2010
- ↑ Serway 1992, p. 383-386
- ↑ Serway 1992, p. 387-389
- 1 2 (en) Louis de Broglie, The Wave Nature of the Electron : Nobel Lecture, December 12, 1929, Fondation Nobel, (lire en ligne [PDF]), p. 13
- ↑ (en) Brigitte Falkenburg, Particle Metaphysics : A Critical Account of Subatomic Reality, Springer Verlag, (ISBN 3-540-33731-8), p. 85
- ↑ (en) Clinton J. Davisson, The Discovery of Electron Waves : Nobel Lecture, December 13, 1937, Fondation Nobel, (lire en ligne [PDF]), p. 8
- ↑ (de) Erwin Schrödinger, « Quantisierung als Eigenwertproblem », Annalen der Physik, vol. 384, no 4, , p. 361-376 (DOI 10.1002/andp.19263840404)
- ↑ (en) John S. Rigden, Hydrogen, Harvard University Press, (ISBN 0-674-01252-6), p. 59–86
- ↑ (en) Bruce Cameron Reed, Quantum Mechanics, Jones & Bartlett Publishers, (ISBN 0-7637-4451-4), p. 275–350
- ↑ (de) Wolfgang Pauli, « Zur Quantenmechanik des magnetischen Elektrons », Zeitschrift für Physik A, vol. 43, no 9-10, , p. 601-623 (DOI 10.1007/BF01397326)
- ↑ (en) Paul A. M. Dirac, « The Quantum Theory of the Electron », Proceedings of the Royal Society of London A, vol. 117, no 778, , p. 610–624 (DOI 10.1098/rspa.1928.0023)
- ↑ (en) Paul A. M. Dirac, Theory of Electrons and Positrons : Nobel Lecture, December 12, 1933, Fondation Nobel, (lire en ligne [PDF])
- ↑ Futura-Sciences, « Antimatière », sur Futura-Sciences (consulté le 13 août 2012)
- ↑ (en) Roger Highfield, « How Dirac predicted antimatter », New Scientist, (lire en ligne)
- ↑ (en) Helge S. Kragh, Quantum Generations : A History of Physics in the Twentieth Century, Princeton University Press, (ISBN 0-691-09552-3), p. 132
- ↑ (en) Frank Gaynor, Concise Encyclopedia of Atomic Energy, The Philosophical Library, , p. 117
- ↑ (en) G. Aruldhas, Quantum Mechanics, Prentice-Hall of India Pvt. Ltd., , 2e éd. (ISBN 81-203-3635-6, lire en ligne), « §15.15 Lamb Shift », p. 404
- ↑ (en) Richard P. Feynman, « The Development of the Space-Time View of Quantum Electrodynamics : Nobel Lecture, December 11, 1965 », Fondation Nobel, (consulté le 22 février 2010)
- ↑ (en) Julian Schwinger, Relativistic Quantum Field Theory : Nobel Lecture, December 11, 1965, Fondation Nobel, (lire en ligne [PDF]), p. 13
- ↑ (en) Sin-Itiro Tomonaga, « Development of Quantum Electrodynamics : Nobel Lecture, May 6, 1966 », Fondation Nobel, (consulté le 22 février 2010)
- ↑ (en) Institut Lorentz, « Lorentz & the Solvay conferences », université de Leyde, (consulté le 20 août 2012)
- ↑ Selon CODATA 2010, elle est de 5,485 799 0 946(22×10-4 u
- 1 2 (en) NIST, « CODATA value : Proton-electron mass ratio », 2006 CODATA recommended values, National Institute of Standards and Technology (consulté le 22 février 2010)
- ↑ Zombeck 2007, p. 14
- ↑ (en) Michael T. Murphy, Victor V. Flambaum, Sébastien Muller et Christian Henkel, « Strong Limit on a Variable Proton-to-Electron Mass Ratio from Molecules in the Distant Universe », Science, vol. 320, no 5883, , p. 1611-1613 (DOI 10.1126/science.1156352, résumé)
- ↑ (en) Jens C. Zorn, George E. Chamberlain et Vernon W. Hughes, « Experimental Limits for the Electron-Proton Charge Difference and for the Charge of the Neutron », Physical Review, vol. 129, no 6, , p. 2566–2576 (DOI 10.1103/PhysRev.129.2566)
- ↑ McFee 2012, p. 141-143
- 1 2 3 Raith et Mulvey 2001
- ↑ Laurent Favart, « Annihilation électron-positon », dans Laurent Favart, Physique auprès des collisionneurs, Bruxelles, Université libre de Bruxelles, 2011-2012 (lire en ligne [PDF]), p. 35-36
- ↑ (en) Nuclear Science Division, « Antimatter », Lawrence Berkeley National Laboratory, (consulté le 16 août 2012)
- ↑ (en) G. Gabrielse, D. Hanneke, T. Kinoshita, M. Nio et B. Odom, « New Determination of the Fine Structure Constant from the Electron g Value and QED », Physical Review Letters, vol. 97, , p. 030802 (DOI 10.1103/PhysRevLett.97.030802)
- ↑ (en) Estia J. Eichten et Michael E. Peskin, « New Tests for Quark and Lepton Substructure », Physical Review Letters, American Physical Society, vol. 50, no 11, , p. 811–814 (DOI 10.1103/PhysRevLett.50.811, Bibcode 1983PhRvL..50..811E)
- ↑ (en) G. Gabrielse, D. Hanneke, T. Kinoshita, M. Nio et B. Odom, « New Determination of the Fine Structure Constant from the Electron g Value and QED », Physical Review Letters, vol. 97, no 3, , p. 030802(1–4) (DOI 10.1103/PhysRevLett.97.030802, Bibcode 2006PhRvL..97c0802G)
- ↑ (en) Perimeter Institute for Theoretical Physics, « More on String Theory », Perimeter Institute for Theoretical Physics, (consulté le 26 janvier 2013)
- ↑ (en) Hans Dehmelt, « A Single Atomic Particle Forever Floating at Rest in Free Space : New Value for Electron Radius », Physica Scripta, vol. T22, , p. 102–110 (DOI 10.1088/0031-8949/1988/T22/016)
- ↑ Griffiths 1995, p. 155
- ↑ (en) Dieter Meschede, Optics, Light and Lasers : The Practical Approach to Modern Aspects of Photonics and Laser Physics, Wiley-VCH, (ISBN 3-527-40364-7, lire en ligne), p. 168
- ↑ (en) Hermann Haken, Hans Christoph Wolf et W. D. Brewer, The Physics of Atoms and Quanta : Introduction to Experiments and Theory, Springer, (ISBN 3-540-20807-0), p. 70
- ↑ (en) R. I. Steinberg, K. Kwiatkowski, W. Maenhaut et N. S. Wall, « Experimental Test of Charge Conservation and the Stability of the Electron », Physical Review D, The American Physical Society, vol. 61, no 2, , p. 2582–2586 (DOI 10.1103/PhysRevD.12.2582)
- ↑ (en) W.-M. Yao, « Review of Particle Physics », Journal of Physics G: Nuclear and Particle Physics, vol. 33, no 1, , p. 77–115 (DOI 10.1088/0954-3899/33/1/001)
- ↑ La NASA affirme qu'il est d'environ 13,77 milliards d'années, consulter (en) NASA, « How Old is the Universe? », NASA, (consulté le 14 janvier 2013)
- ↑ (en) Robert Mann (professeur à l'université de Waterloo, Ontario, Canada), An Introduction to Particle Physics and the Standard Model, CRC Press, (ISBN 978-1-4200-8298-2), p. 544-546
- ↑ (en) M. C. Gupta, Atomic and Molecular Spectroscopy, New Age Publishers, (ISBN 81-224-1300-5), p. 81
- 1 2 (en) B. Odom, D. Hanneke, B. D'Urso et G. Gabrielse, « New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron », Physical Review Letters, vol. 97, , p. 030801 (DOI 10.1103/PhysRevLett.97.030801)
- ↑ Anastopoulos 2008, p. 261–262
- ↑ Zitoun 2000, p. 50-51
- ↑ Serway 1992, p. 252-257
- ↑ Serway 1992, p. 420-424
- 1 2 3 Munowitz 2005, p. 162-218
- ↑ Serway 1992, p. 464 et 465 (fig. 3)
- ↑ McFee 2012, p. 158-159
- ↑ (en) Dave Fehling, « The Standard Model of Particle Physics : A Lunchbox's Guide », The Johns Hopkins University, (consulté le 13 août 2012)
- ↑ (en) Paul H. Frampton, P. Q. Hung et Marc Sher, « Quarks and Leptons Beyond the Third Generation », Physics Reports, vol. 330, , p. 263–348 (DOI 10.1016/S0370-1573(99)00095-2)
- ↑ Anastopoulos 2008, p. 236–237
- ↑ (en) Gordon Kane, « Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics? », Scientific American, (lire en ligne)
- ↑ Griffiths 1995, p. 115
- ↑ (en) John Taylor, The New Physics, Cambridge University Press, (ISBN 0-521-43831-4), p. 464
- ↑ (en) I. Levine, D. Koltick, B. Howell, E. Shibata, J. Fujimoto, T. Tauchi, K. Abe, T. Abe et I. Adachi, « Measurement of the Electromagnetic Coupling at Large Momentum Transfer », Physical Review Letters, vol. 78, , p. 424–427 (DOI 10.1103/PhysRevLett.78.424)
- ↑ Griffiths 1995, p. 190
- 1 2 (en) Henning Genz (trad. Karin Heusch), Nothingness : The Science of Empty Space [« Die Entdeckung des Nichts »], Helix Books et Perseus Books, (ISBN 0-7382-0061-1, présentation en ligne), p. 241-243 et 245-247 Une autre version de l'ouvrage a été publiée en 2001 (ISBN 978-0738206103).
- ↑ (en) John Gribbin, « More to Electrons Than Meets the Eye », New Scientist, , p. 15 (lire en ligne) :
« The researchers discovered that the effects of this cloud of virtual particles in shielding the electron's charge was reduced the closer a particle penetrated the core of the electron. The true value of the electromagnetic charge near the center of the electron was far greater than at the edge. »
(frais de consultation requis) - ↑ Greene 2000, p. 284.
- ↑ (en) Hitoshi Murayama, Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories : La Thuile, Italy, coll. « Rencontres de Moriond / 42 », (lire en ligne), « Supersymmetry Breaking Made Easy, Viable and Generic », donne 9 % de différence de masse pour un électron de la taille de la longueur de Planck.
- ↑ (en) Julian Schwinger, « On Quantum-Electrodynamics and the Magnetic Moment of the Electron », Physical Review, vol. 73, no 4, , p. 416–417 (DOI 10.1103/PhysRev.73.416)
- ↑ (en) Kerson Huang, Fundamental Forces of Nature : The Story of Gauge Fields, World Scientific, (ISBN 981-270-645-3), p. 123–125
- ↑ (en) Leslie L. Foldy et Siegfried A. Wouthuysen, « On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit », Physical Review, vol. 78, , p. 29–36 (DOI 10.1103/PhysRev.78.29)
- ↑ (en) Burra G. Sidharth, « Revisiting Zitterbewegung », International Journal of Theoretical Physics, vol. 48, , p. 497–506 (DOI 10.1007/s10773-008-9825-8)
- ↑ (en) Robert S. Elliott, « The History of Electromagnetics as Hertz Would Have Known It », IEEE Transactions on Microwave Theory and Techniques, vol. 36, no 5, , p. 806–823 (DOI 10.1109/22.3600, résumé) Texte disponible pour les abonnés.
- ↑ Munowitz 2005, p. 140
- ↑ Serway 1989, p. 166-167, 276-277
- ↑ (en) Benjamin Crowell, Electricity and Magnetism, Light and Matter, (ISBN 0-9704670-4-4, lire en ligne), p. 129–145
- ↑ (en) Bo Thidé (Membre du Swedish Institute of Space Physics), Electromagnetic Field Theory, Uppsala, Suède, Upsilon Books, , 2e éd., 272 p. (ISBN 9780486477732, lire en ligne), p. 122
- ↑ Munowitz 2005, p. 160
- ↑ (en) Rohan Mahadevan, Ramesh Narayan et Insu Yi, « Harmony in Electrons : Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field », Astrophysical Journal, vol. 465, , p. 327–337 (DOI 10.1086/177422, lire en ligne)
- ↑ (en) Fritz Rohrlich, « The Self-Force and Radiation Reaction », American Journal of Physics, vol. 68, no 12, , p. 1109–1112 (DOI 10.1119/1.1286430)
- ↑ (en) Howard Georgi, The New Physics, Cambridge University Press, (ISBN 0-521-43831-4), « Grand Unified Theories », p. 427
- ↑ (en) George J. Blumenthal et Robert J. Gould, « Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases », Reviews of Modern Physics, vol. 42, , p. 237–270 (DOI 10.1103/RevModPhys.42.237)
- ↑ Zombeck 2007, p. 393 et 396
- ↑ (en) Arthur H. Compton, X-Rays as a Branch of Optics : Nobel Lecture, December 12, 1927, Fondation Nobel, (lire en ligne [PDF]), p. 17
- ↑ (en) Szu-yuan Chen, Anatoly Maksimchuk et Donald Umstadter, « Experimental Observation of Relativistic Nonlinear Thomson Scattering », Nature, vol. 396, , p. 653–655 (DOI 10.1038/25303)
- ↑ (en) Robert Beringer et C. G. Montgomery, « The Angular Distribution of Positron Annihilation Radiation », Physical Review, vol. 61, no 5–6, , p. 222–224 (DOI 10.1103/PhysRev.61.222)
- ↑ (en) Jerry Wilson et Anthony Buffa, College Physics, Prentice Hall, , 4e éd. (ISBN 0-13-082444-5), p. 888
- ↑ (en) Jörg Eichler, « Electron–Positron Pair Production in Relativistic Ion–Atom Collisions », Physics Letters A, vol. 347, no 1–3, , p. 67–72 (DOI 10.1016/j.physleta.2005.06.105)
- ↑ (en) J. H. Hubbell, « Electron Positron Pair Production by Photons : A historical overview », Radiation Physics and Chemistry, vol. 75, no 6, , p. 614–623 (DOI 10.1016/j.radphyschem.2005.10.008)
- ↑ (en) Chris Quigg, TASI 2000 : Flavor Physics for the Millennium, Boulder, Colorado, arXiv, (présentation en ligne), « The Electroweak Theory », p. 80
- ↑ Augustin 2008, p. 119.
- ↑ Raymond Serway (trad. Robert Morin), Physique I : Mécanique, Les éditions HRW Ltée, (ISBN 0-03-926355-X), p. 125-126
- ↑ Allô prof, « 6020 – Les modèles atomiques », Allô prof, (consulté le 14 août 2012) : « Un atome neutre possède toujours autant de protons que d'électrons. »
- ↑ asp, « Ion », Assistance scolaire personnalisée, (consulté le 14 août 2012)
- ↑ Syndicat CFDT de l'énergie atomique, Le Dossier électronucléaire, Seuil, coll. « Points Sciences », (ISBN 978-2020054034), p. 21
- ↑ CEA, « Au cœur de la matière : les atomes (1/4) », Commissariat à l'énergie atomique et aux énergies alternatives, (consulté le 3 mars 2013)
- ↑ Serway 1992, p. 475-479
- ↑ (en) Steven Holzner, Quantum Physics For Dummies, For Dummies, , 336 p. (ISBN 978-0470381885, lire en ligne), p. 251
- ↑ (en) Robert S. Mulliken, « Spectroscopy, Molecular Orbitals, and Chemical Bonding », Science, vol. 157, no 3784, , p. 13–24 (DOI 10.1126/science.157.3784.13)
- ↑ (en) Eric H. S. Burhop, The Auger Effect and Other Radiationless Transitions, New York, Cambridge University Press, , p. 2–3
- 1 2 (en) Claus Grupen, Instrumentation in Elementary Particle Physics, VIII, vol. 536, Istanbul, Dordrecht, D. Reidel Publishing Company, coll. « AIP Conference Proceedings », (DOI 10.1063/1.1361756, présentation en ligne), « Physics of Particle Detection », p. 3–34
- ↑ (en) David Jiles, Introduction to Magnetism and Magnetic Materials, CRC Press, (ISBN 0-412-79860-3), p. 280–287
- ↑ (en) Per Olov Löwdin, Erkki Erkki Brändas et Eugene S. Kryachko, Fundamental World of Quantum Chemistry : A Tribute to the Memory of Per-Olov Löwdin, Springer, (ISBN 1-4020-1290-X), p. 393–394
- ↑ (en) Eden Francis, « Valence Electrons », Clackamas Community College, (consulté le 29 décembre 2012)
- ↑ Pauling 1960
- ↑ (en) Donald Allan McQuarrie et John Douglas Simon, Physical Chemistry : A Molecular Approach, University Science Books, (ISBN 0-935702-99-7), p. 325–361
- ↑ (en) R. Daudel, R.F.W. Bader, M.E. Stephens et D.S. Borrett, « The Electron Pair in Chemistry », Canadian Journal of Chemistry, vol. 52, , p. 1310–1320 (lire en ligne)
- ↑ John W. ill, Ralph H. Petrucci, Martin Lamoureux et Martin Dion, Chimie générale, Saint-Laurent, Canada, Éditions du Renouveau Pédagogique, (ISBN 2-7613-1206-6), p. 282
- ↑ Paul Arnaud, Cours de chimie physique, Paris, Dunod, (ISBN 2-04-018602-6), p. 412-415
- ↑ Donald A. Mc Quarrie et Peter A. Rock (trad. Paul Depovere), Chimie générale, De Boeck Université, , 3e éd. (ISBN 2-8041-1496-1), p. 766-768
- ↑ (en) Vladimir A. Rakov et Martin A. Uman, Lightning : Physics and Effects, Cambridge University Press, (ISBN 0-521-03541-4), p. 4
- ↑ (en) Gordon R. Freeman, « Triboelectricity and some associated phenomena », Materials science and technology, vol. 15, no 12, , p. 1454–1458
- ↑ (en) Keith M. Forward, Daniel J. Lacks et R. Mohan Sankaran, « Methodology for Studying Particle–Particle Triboelectrification in Granular Materials », Journal of Electrostatics, vol. 67, no 2–3, , p. 178–183 (résumé)
- ↑ Serway 1989, p. 2-4
- ↑ (en) Liang-fu Lou, Introduction to Phonons and Electrons, World Scientific, (ISBN 978-981-238-461-4)
- ↑ (en) Bhag S. Guru et Hüseyin R. Hızıroğlu, Electromagnetic Field Theory, Cambridge University Press, (ISBN 0-521-83016-8), p. 138 et 276
- ↑ (en) M. K. Achuthan et K. N. Bhat, Fundamentals of Semiconductor Devices, Tata McGraw-Hill, (ISBN 0-07-061220-X), p. 49–67
- 1 2 (en) J. M. Ziman, Electrons and Phonons : The Theory of Transport Phenomena in Solids, Oxford University Press, (ISBN 0-19-850779-8), p. 260
- ↑ (en) Peter Main, « When Electrons Go With the Flow : Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise », New Scientist, vol. 1887, , p. 30 (lire en ligne)
- ↑ (en) Glenn R. Blackwell, The Electronic Packaging Handbook, CRC Press, (ISBN 0-8493-8591-1), p. 6.39–6.40
- ↑ (en) Alan Durrant, Quantum Physics of Matter : The Physical World, CRC Press, (ISBN 0-7503-0721-8), p. 43, 71–78
- ↑ (en) John Bardeen, Electron-Phonon Interactions and Superconductivity : Nobel Lecture, December 11, 1972, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 16
- ↑ (en) Leon N. Cooper, Microscopic Quantum Interference Effects in the Theory of Superconductivity : Nobel Lecture, December 11, 1972, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 21
- ↑ (en) Robert Schrieffer, Macroscopic Quantum Phenomena from Pairing in Superconductors : Nobel Lecture, December 11, 1972, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 12
- ↑ Charles Kittel (trad. Nathalie Bardou, dre ès sciences physiques, et Évelyne Kolb, maître de conférence à l'université Pierre-et-Marie-Curie), Physique de l'état solide, Paris, Dunod, , 7e éd. (ISBN 2-10-003267-4), p. 320-322
- ↑ Futura-Sciences, « Chargeon », Futura-Sciences, (consulté le 14 août 2012)
- ↑ (en) Yodchay Jompol, C. J. B. Ford, J. P. Griffiths, I. Farrer, G. A. Jones, D. Anderson, D. A. Ritchie, T. W. Silk et A. J. Schofield, « Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid », Science, vol. 325, no 5940, , p. 597-601 (DOI 10.1126/science.1171769, résumé, lire en ligne)
- ↑ Feynman 1987, p. 109
- ↑ (en) Dionysius Lardner, Treatise on Heat, Longman, Rees, Orme, Brown, Green & Longman, (lire en ligne) :
« On appelle « incandescence » l'état dans lequel un corps chauffé, naturellement incapable d'émettre de la lumière, devient lumineux[trad 2]. »
- ↑ (en) Bernard Valeur et Mario N. Berberan-Santos, « A Brief History of Fluorescence and Phosphorescence before the Emergence of Quantum Theory », J. Chem. Educ., vol. 88, no 6, , p. 731–738 (DOI 10.1021/ed100182h)
- ↑ Serway 1992, p. 130 (lire en ligne) :
« Les sources du rayonnement électromagnétique sont des charges accélérées. »
- ↑ François Rothen, Physique générale : La physique des sciences de la nature et de la vie, Presses Polytechniques et Universitaires Romandes, , 862 p. (ISBN 978-2880743963, lire en ligne), p. 416 :
« Un rayonnement magnétique, quel qu'il soit, est nécessairement produit par l'accélération de charges électriques. »
- ↑ McFee 2012, p. 130
- ↑ Feynman 1987, p. 137-145
- ↑ Serway 1992, p. 301-303
- ↑ Bernard Valeur, « Les Couleurs des animaux », CNRS, (consulté le 17 août 2012)
- ↑ (en) Max Born (auteur), Emil Wolf (auteur), A. B. Bhatia (contributeur), P. C. Clemmow (contributeur), D. Gabor (contributeur), A. R. Stokes (contributeur), A. M. Taylor (contributeur), P. A. Wayman (contributeur) et W. L. Wilcock (contributeur), Principles of Optics : Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Cambridge University Press, , 7e éd., 986 p. (ISBN 978-0521642224), p. 742
- ↑ (en) James William Rohlf, Modern Physics from α to Z°, New York, John Wiley's & Sons, Inc., (ISBN 0-471-57270-5), p. 125
- ↑ Frauenfelder et Henley 1991, p. 42-43
- ↑ Zitoun 2000, p. 84-85
- ↑ Frauenfelder et Henley 1991, p. 43
- ↑ Zitoun 2000, p. 81
- ↑ (en) Pavel A. Cherenkov, Radiation of Particles Moving at a Velocity Exceeding That of Light, and Some of the Possibilities for Their Use in Experimental Physics : Nobel Lecture, December 11, 1958, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 15
- ↑ (en) Il´ja M. Frank, Optics of Light Sources Moving in Refractive Media : Nobel Lecture, December 11, 1958, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 27
- ↑ (en) Igor Y. Tamm, General Characteristics of Radiation Emitted by Systems Moving with Super-Light Velocities with Some Applications to Plasma Physics : Nobel Lecture, December 11, 1958, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 13
- ↑ Éric Gourgoulhon, Relativité restreinte : Des particules à l'astrophysique, EDP Sciences, coll. « Savoirs actuels », , 804 p. (ISBN 978-2759800674, présentation en ligne, lire en ligne), p. 101
- ↑ Serway 1992, p. 348. La formule est présentée différemment, mais par une mise en évidence de
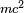 , on retrouve la formule.
, on retrouve la formule. - ↑ (en) « Special Relativity », Stanford Linear Accelerator Center, (consulté le 27 février 2010)
- ↑ Serway 1992, p. 450
- ↑ (en) Luis W. Alvarez et W. Peter Trower, « K-Electron Capture by Nuclei », dans Emilio Segré, Discovering Alvarez : Selected works of Luis W. Alvarez, with commentary by his students and colleagues, University of Chicago Press, (ISBN 0-226-81304-5), chap. 3, p. 11-12
- ↑ (en) Luis W. Alvarez, « Nuclear K Electron Capture », Physical Review, vol. 52, , p. 134–135 (DOI 10.1103/PhysRev.52.134)
- ↑ (en) European Space Agency, « So, How Did Everything Start? ...A Timeline for the Universe », European Space Agency, (consulté le 13 août 2012)
- ↑ (en) NASA, « The Big Bang », NASA, (consulté le 13 août 2012)
- ↑ (en) Lawrence Berkely National Laboratory, « Beta Decay », Lawrence Berkely National Laboratory, (consulté le 6 août 2012)
- ↑ (en) R. A. Schumacher, « Cosmic Ray Muons », dans 33.340 Modern Physics Laboratory, Carnegie Mellon University, , 3.1e éd. (lire en ligne [PDF]), p. 1
- ↑ (en) K. Bernlöhr, « Development of Cosmic-ray Air Shower », Max-Planck-Institut Für Kernphysik in Heidelberg, (consulté le 13 août 2012)
- ↑ (en) Paul F. Lurquin, The Origins of Life and the Universe, Columbia University Press, (ISBN 0-231-12655-7), p. 2
- ↑ (en) N. Jarosik et et al., « Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations : Sky Maps, Systematic Errors, and Basic Results », The Astrophysical Journal Supplement Series, vol. 192, , p. 14 (DOI 10.1088/0067-0049/192/2/14, Bibcode 2011ApJS..192...14J, arXiv 1001.4744)
- ↑ (en) Joseph Silk, The Big Bang : The Creation and Evolution of the Universe, Macmillan, , 3e éd. (ISBN 0-8050-7256-X), p. 110–112 et 134–137
- ↑ (en) Vic Christianto et Florentin Smarandache, « Thirty Unsolved Problems in the Physics of Elementary Particles », Progress in Physics, vol. 4, , p. 112–114 (lire en ligne)
- ↑ (en) Edward W. Kolb, « The Development of Baryon Asymmetry in the Early Universe », Physics Letters B, vol. 91, no 2, , p. 217–221 (résumé)
- ↑ (en) Eric Sather, « The Mystery of Matter Asymmetry », Beam Line, University of Stanford, , p. 31-37 (lire en ligne [PDF])
- ↑ (en) Scott Burles, Kenneth M. Nollett et Michael S. Turner, « Big-Bang Nucleosynthesis : Linking Inner Space and Outer Space », ArXiv, University of Chicago, (lire en ligne)
- ↑ (en) A. M. Boesgaard et G Steigman, « Big Bang Nucleosynthesis – Theories and Observations », Annual Review of Astronomy and Astrophysics, vol. 23, no 2, , p. 319–378 (lire en ligne)
- 1 2 (en) Rennan Barkana, « The First Stars in the Universe and Cosmic Reionization », Science, vol. 313, no 5789, , p. 931–934 (résumé)
- ↑ (en) E. Margaret Burbidge, G. R. Burbidge, William A. Fowler et F. Hoyle, « Synthesis of Elements in Stars », Reviews of Modern Physics, vol. 29, no 4, , p. 548–647
- ↑ (en) L. S. Rodberg et V. F. Weisskopf, « Fall of Parity : Recent Discoveries Related to Symmetry of Laws of Nature », Science, vol. 125, no 3249, , p. 627–633
- ↑ (en) Chris L. Fryer, « Mass Limits For Black Hole Formation », The Astrophysical Journal, vol. 522, no 1, , p. 413–418 (lire en ligne [PDF])
- ↑ Serway 1992, p. 371-372
- ↑ Le physicien britannique Stephen Hawking est le premier à publier cette hypothèse en 1975 : (en) S. W. Hawking, « Particle Creation by Black Holes », Communications in Mathematical Physics, vol. 43, , p. 199-220
- Erratum ibid., 46, 206 (1976) Voir en ligne.
- ↑ (en) Maulik K. Parikh et F Wilczek, « Hawking Radiation as Tunneling », Physical Review Letters, vol. 85, no 24, , p. 5042–5045 (résumé)
- ↑ (en) S. W. Hawking, « Black Hole Explosions? », Nature, vol. 248, , p. 30–31 (résumé)
- ↑ (en) F. Halzen et Dan Hooper, « High-energy Neutrino Astronomy : The cosmic ray connection », Reports on Progress in Physics, vol. 66, , p. 1025–1078 (résumé)
- ↑ (en) James F. Ziegler, « Terrestrial Cosmic Ray Intensities », IBM Journal of Research and Development, vol. 42, no 1, , p. 117–139
- ↑ (en) Christine Sutton, « Muons, Pions and Other Strange Particles », New Scientist, (lire en ligne)
- ↑ (en) Stuart Wolpert, « Scientists Solve 30-Year-Old Aurora Borealis Mystery », University of California, (consulté le 28 février 2010)
- ↑ (en) Donald A. Gurnett et R. R. Anderson, « Electron Plasma Oscillations Associated with Type III Radio Bursts », Science, vol. 194, no 4270, , p. 1159–1162 (résumé)
- ↑ (en) Hans G. Dehmelt, Experiments With an Isolated Subatomic Particle at Rest : Nobel Lecture, December 8, 1989, Oslo, Fondation Nobel, (lire en ligne [PDF]), p. 586
- ↑ (en) Philip Ekstrom, « The Isolated Electron », Scientific American, vol. 243, no 2, , p. 91–101 (lire en ligne [PDF])
- ↑ (en) Swedish Research Council, « Electron Filmed for the First Time Ever », Phys.org, (lire en ligne)
- ↑ (en) J. Mauritsson, P. Johnsson, E. Mansten, M. Swoboda, T. Ruchon, A. L'huillier et K. J. Schafer, « Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope », Physical Review Letters, vol. 100, , p. 073003 (lire en ligne)
- ↑ (en) Andrea Damascelli, « Probing the Electronic Structure of Complex Systems by ARPES », Physica Scripta, vol. T109, , p. 61-74 (résumé)
- ↑ (en) Rolf Erni, M. D. Rossell, C. Kisielowski et U. Dahmen, « Atomic-Resolution Imaging with a Sub-50-pm Electron Probe », Physical Review Letters, vol. 102, no 9, , p. 096101 (résumé)
- ↑ (en) John W. Kitzmiller, Television Picture Tubes and Other Cathode-Ray Tubes: Industry and Trade Summary, DIANE Publishing, (ISBN 0-7881-2100-6), p. 3–5
- ↑ (en) John Elmer, « Standardizing the Art of Electron-Beam Welding », Lawrence Livermore National Laboratory, (consulté le 28 février 2010)
- ↑ Serway 1992, p. 502-504
- ↑ (en) Robert B. Friedman et Rick Kessler, The Photoelectric Effect & Its Applications, Yerkes Summer Institute de l'université de Chicago, (lire en ligne [PDF])
- ↑ Michel Crozon, La Matière première : La recherche des particules fondamentales et leurs interactions, Seuil, , p. 340
- 1 2 3 4 5 6 7 8 9 10 11 12 J. P. Mathieu (dir.), A. Kastler (dir. et lauréat du prix Nobel de physique) et P. Fleury (dir. et directeur honoraire de l'Institut optique), Dictionnaire de physique, Masson et Eyrolles, , 3e éd., 567 p. (ISBN 978-2225824159), p. 155-156
- 1 2 Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, de Boeck, , 912 p. (ISBN 9782804175542, présentation en ligne), p. 169-170
- ↑ John C. Kotz et Paul M. Treichel Jr, Chimie générale, Éditions de la Chenelière, (ISBN 978-2-8041-5231-4, lire en ligne), p. 170
- 1 2 Jésus M. Tharrats Vidal, « Sur un schéma de l'électron », J. Phys. Radium, vol. 13, no 5, , p. 283-288 (DOI 10.1051/jphysrad:01952001305028300, lire en ligne)
- ↑ Archives Henri Poincaré, « Hendrik Antoon Lorentz », Laboratoire d'histoire des sciences et de philosophie, université de Lorraine, (consulté le 3 mars 2013)
- ↑ « "modèle de l'électron libre" - Recherche Google », Google, (consulté le 14 février 2015)
- ↑ « "gaz d'électrons" - Recherche Google », Google, (consulté le 14 février 2015)
Annexes
Bibliographie
- (en) Charis Anastopoulos, Particle Or Wave : The Evolution of the Concept of Matter in Modern Physics, Princeton University Press, (ISBN 0-691-13512-6)
- Jean-Eudes Augustin, « Électron », dans Encyclopædia Universalis, vol. 8 : Égypte - Étrusques, Paris, Encyclopædia Universalis,
- (de) Alfred Heinrich Bucherer, « Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie », Physikalische Zeitschrift, vol. 9, no 22,
- (en) Jed Z. Buchwald et Andrew Warwick, Histories of the Electron : The Birth of Microphysics, Boston, MIT Press, (ISBN 0-262-52424-4)
- (en) Arthur N. Cox (dir.), Allen's Astrophysical Quantities, Springer, , 4e éd. (ISBN 978-0-387-95189-8)
- (en) Lorenzo J. Curtis, Atomic Structure and Lifetimes : A Conceptual Approach, Cambridge University Press, (ISBN 0-521-53635-9), p. 74
- (en) Per F. Dahl, Flash of the Cathode Rays : A History of J.J. Thomson's Electron, CRC Press, , 526 p. (ISBN 978-0750304535)
- Richard Feynman, Lumière et matière : Une étrange histoire, InterÉditions, coll. « Point Sciences », , 214 p. (ISBN 2-02-014758-0)
- (en) Hans Frauenfelder et Ernest M. Henley, Subatomic Physics, Upper Saddle River, New Jersey, Prentice Hall, , 2e éd. (ISBN 0-13-859430-9)
- Brian Greene (trad. Céline Laroche, préf. Trinh Xuan Thuan), L'Univers élégant [« The Elegant Universe »], Gallimard, coll. « Folio Essais », , 470 p. (ISBN 978-2-070-30280-2)
- (en) David J. Griffiths, Introduction to Quantum Mechanics, Upper Saddle River, New Jersey, Prentice Hall, (ISBN 0-13-124405-1, présentation en ligne)
- (de) Walter Kaufmann, « Die elektromagnetische Masse des Elektrons », Physikalische Zeitschrift, vol. 4, no 1b,
- (de) Walter Kaufmann, « Über die Konstitution des Elektrons », Sitzungsberichte der Königlich Preußische Akademie der Wissenschaften, vol. 45,
- (en) Oliver Heaviside, « Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge », Electrical papers, vol. 2,
- J. P. McEvoy, Oscar Zarate (illustrateur) et Judy Groves (diagrammes et graphiques), La Théorie quantique en images, EDP sciences, coll. « Aperçu », (ISBN 978-2-759-81229-5, présentation en ligne)
- Isaac McFee, Physique au lit : Vitesse et magnétisme pour être plus intelligent [« The Bedside Book of Physics »], Trécarré, coll. « La Science au lit », (ISBN 978-2895686002, présentation en ligne), p. 178
- (en) Arthur I. Miller, Albert Einstein’s Special Theory of Relativity : Emergence (1905) and early interpretation (1905–1911), Reading (Massachusetts), Addison–Wesley, (ISBN 0-201-04679-2)
- (en) Peter J. Mohr, Barry N. Taylor et David B. Newell, « CODATA Recommended Values of the Fundamental Physical Constants », Reviews of Modern Physics, vol. 80, , p. 633–730 (DOI 10.1103/RevModPhys.80.633)
- (en) Michael Munowitz, Knowing, The Nature of Physical Law, Oxford University Press, (ISBN 0-19-516737-6)
- (en) Linus C. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crystals : An introduction to modern structural chemistry, Ithaca (New York), Cornell University Press, , 3e éd. (ISBN 0-8014-0333-2, résumé), p. 4–10
- (en) Wilhelm Raith et Thomas Mulvey, Constituents of Matter : Atoms, Molecules, Nuclei and Particles, CRC Press, (ISBN 0-8493-1202-7), p. 777–781
- Jean Rosmorduc, Une histoire de la physique et de la chimie : De Thalès à Einstein, Seuil, coll. « Points Sciences », (ISBN 9782020089906)
- (en) George Frederick Charles Searle, « On the Steady Motion of an Electrified Ellipsoid », Philosophical Magazine, vol. 44, no 269,
- Raymond A. Serway (trad. Robert Morin), Physique II : Électricité et magnétisme [« Physics for Scientists and Engineers/with Modern Physics. Volume 2 »], Montréal (Québec), Éditions études vivantes, , 2e éd. (ISBN 0-03-926211-1)
- Raymond A. Serway (trad. Robert Morin et Céline Temblay), Physique III : Optique et physique moderne [« Physics for Scientists and Engineers / With Modern Physics »], Laval (Québec), Éditions Études Vivantes, , 3e éd., 776 p. (ISBN 2-7607-0542-0, présentation en ligne)
- (en) Boris M. Smirnov, Physics of Atoms and Ions, Springer, (ISBN 0-387-95550-X)
- (en) Joseph John Thomson, « On the Electric and Magnetic Effects produced by the Motion of Electrified Bodies », Philosophical Magazine, vol. 11, no 68,
- Kip S. Thorne (trad. Alain Bouquet et Jean Kaplan, préf. Stephen Hawking), Trous noirs et distorsions du temps : l'héritage sulfureux d'Einstein, Flammarion, coll. « Champs », , 654 p. (ISBN 9782082112215)
- (en) Edmund Taylor Whittaker, A History of the Theories of Aether and Electricity, vol. 1 : The Classical Theories, Londres, Nelson, , 2e éd.
- (en) Edmund Taylor Whittaker, A History of the Theories of Aether and Electricity, vol. 2 : The modern theories 1900-1926, Londres, Nelson, , 2e éd.
- (en) Scott Walter, « Minkowski, Mathematicians, and the Mathematical Theory of Relativity », dans H. Goenner, J. Renn, J. Ritter et T. Sauer, Einstein Studies, Birkhäuser, , p. 45–86
- Robert Zitoun (professeur à l'université de Savoie (Annecy-le-Vieux)), Introduction à la physique des particules, Paris, Dunod, coll. « Sciences Sup », , 2e éd., 144 p. (ISBN 9782100487783, présentation en ligne), p. 50-51
- (en) Martin V. Zombeck, Handbook of Space Astronomy and Astrophysics, Cambridge University Press, , 3e éd. (ISBN 0-521-78242-2)
Articles connexes
- Électron Auger
- Effet photoélectrique
- Excitation (physique)
- Particule β
- Mobilité des porteurs de charge
- Diffusion Compton
- Liste d'applications des propriétés de l'électron
Liens externes
- (en) Valeur CODATA pour le rayon classique de l'électron sur le site du NIST.
- (en) John Baez, « The Classical Electron Radius » dans Length Scales in Physics, 12 février 2010
- (en) W.-M. Yao et al., « eMASS (atomic mass units u) », J. Phys. G, Particle Data Group, vol. 33, no 1, (lire en ligne [PDF]) Caractéristiques de l'électron
- Ilarion Pavel, « La mesure par Millikan de la charge de l'électron », BibNum, (analyse de Ilarion Pavel, qui se dit « ingénieur en chef des mines, docteur en physique théorique »)
- Notices d’autorité : Gemeinsame Normdatei • Bibliothèque nationale de la Diète
- Portail de la physique
- Portail de l’électricité et de l’électronique
- Portail de la chimie
- Portail de l’énergie