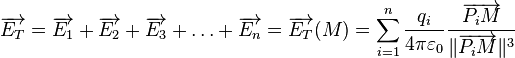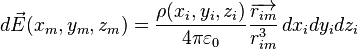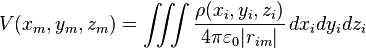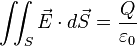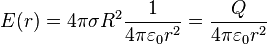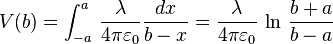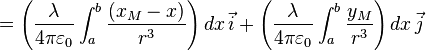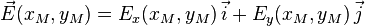Électrostatique

Pour les articles homonymes, voir Statique.

Foudre engendrant un éclair lumineux au-dessus de Oradea en Roumanie

L'électrostatique est la branche de la physique qui étudie les phénomènes créés par des charges électriques statiques pour l'observateur.

Depuis l'Antiquité il est connu que certains matériaux, dont l'ambre, attirent des objets de petite taille après avoir été frottés. Le mot grec pour ambre, ήλεκτρον (électron), a donné son nom à de nombreux domaines scientifiques. L'électrostatique décrit notamment les forces qu'exercent les charges électriques entre elles : il s'agit de la loi de Coulomb. Cette loi énonce que la force 'F' créée par une charge 'Q' sur une autre charge 'q' est proportionnelle au produit de ces deux charges et à l'inverse au carré de la distance les séparant.

Bien qu'elles semblent, à notre échelle, relativement faibles, les forces d'origine électrostatique sont extraordinairement puissantes. Entre des charges électriques élémentaires (principalement les protons et les électrons), elles sont supérieures de 40 ordres de grandeur à la force de gravitation. Si elles nous semblent si faible, c'est justement parce qu'à cause même de l'intensité de ces forces, les charges positives et négatives sont forcées d'être quasi exactement à l'équilibre et que les forces d'attraction et de répulsions s'annulent à l'échelle macroscopique. En réalité, pour comprendre leur force réelle, il faut réaliser que ce sont elles qui font que des objets solides ne s'interpénètrent pas et qui font la cohésion des matériaux les plus durs. Si on réussissait à éliminer, ne serait-ce que la dernière couche d'électrons des atomes, la matière se désintégrerait rien que par les forces de répulsion qui apparaîtraient entre les noyaux.

Les domaines d'étude couverts par l'électrostatique sont nombreux :

l'électricité statique,
l'explosion des silos à grain
certaines technologies de photocopieurs
la foudre...

Les lois de l'électrostatique se sont avérées également utiles en:

biophysique,
l'étude des protéines.
nanotechnologie (Concevoir un moteur à l'échelle des nanotechnologies, est plus réalisable en utilisant les forces électrostatiques que les forces électromagnétiques.)

Ses extensions aux charges en mouvement sont étudiées dans le cadre de l'électromagnétisme qui elle-même est généralisée par l'électrodynamique quantique.

Généralités

Il existe une expérience simple, que tout le monde peut faire, permettant de percevoir une force électrostatique : il suffit de frotter une règle en plastique avec un chiffon bien sec et de l’approcher de petits bouts de papier : c’est l’électrisation. Les papiers se collent à la règle et y restent tant que les charges ne sont pas équilibrées. L’expérience est simple à réaliser, cependant l’interprétation n’est pas simple puisque, si la règle est chargée par frottement, les bouts de papiers ne le sont pas a priori. Une autre expérience du même style consiste à observer qu'un filet d’eau est dévié si on en approche un film de cellophane.

Plus simplement, une expérience commune des effets de l'électrostatique est la sensation de recevoir une décharge en attrapant un chariot par temps très sec, en descendant ou montant dans une voiture ou en retirant un vêtement en tissu synthétique. Ce sont des phénomènes où il s’est produit une accumulation de charges, d’électricité statique.

À partir de là, on peut considérer deux catégories de corps : les isolants, ou diélectriques, où l’état d’électrisation se conserve localement et les conducteurs où cet état se répartit sur la surface du conducteur. L’électrisation des corps a pu être observée grâce aux propriétés isolantes de l’air sec, qui empêche l’écoulement vers la terre des charges créées par frottement.

La distinction entre isolants et conducteurs n’a rien d’absolu ; la résistivité n’est jamais infinie (mais très grande) et, par exemple, un papier sec isolant peut devenir conducteur s'il est humidifié avec de l'eau.

Les charges électriques libres, pratiquement absentes dans les bons isolants, peuvent y être créées facilement en fournissant à un électron, normalement lié à un édifice atomique, une quantité d’énergie suffisante pour l’en dégager (par irradiation ou échauffement, par exemple). À une température de 3 000 °C, il n’y a plus d’isolants, mais seulement des conducteurs.

On constate aussi expérimentalement qu’il existe deux sortes de charges que l’on distingue par leur signe, et que la matière est constituée de particules de charges variées, toutes multiples de celle de l’électron, appelée « charge élémentaire » ; cependant en électrostatique on se contentera de dire que lorsqu'un objet est chargé en volume, il contient une densité volumique de charge 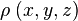$\rho \; ( x , y , z )$ . Ceci correspond à une approximation statistique, compte tenu de la petitesse de la charge élémentaire.

De même une petite expérience permet de démontrer l’importance de l’électricité statique : il suffit de charger un peigne en plastique (en se peignant avec des cheveux secs) puis d’approcher le peigne chargé d’une lampe à tube à néon : dans l’obscurité, en approchant le peigne du tube, celui-ci s’allume localement. Le champ électrique produit par le peigne est suffisant pour exciter le gaz à l’intérieur du tube. D’où l’importance de l’électricité statique : si le champ électrique d’un simple peigne est suffisant pour exciter un gaz, la décharge d’électricité statique dans un appareil électronique sensible peut aussi le détruire.

Formules de base

L'équation fondamentale de l'électrostatique est la loi de Coulomb, qui décrit la force d'interaction entre deux charges ponctuelles. Dans un milieu homogène, le seul cas que nous considérerons dans cet article, le vide par exemple, elle s'écrit :

Force de 1 sur 2 = - Force de 2 sur 1 :

\overrightarrow{F_1}(2) = q_2 \frac{q_1 \overrightarrow{e_r}} {4 \pi \varepsilon r_{12}^2} = q_2 \frac{q_1 \overrightarrow{r_{12}}}{4 \pi \varepsilon r_{12}^2} = - q_1\frac{q_2 \overrightarrow{r_{21}}}{4 \pi \varepsilon r_{21}^2}= -\overrightarrow{F_2}(1)

Ici, la constante ε est une constante caractéristique du milieu, appelée la « permittivité ». Dans le cas du vide, on la note ε₀. La permittivité de l'air étant de 0,5 ‰ supérieure à celle du vide, elle lui est donc souvent assimilée.

Cette écriture traduit le fait que deux charges de même signe se repoussent et que deux charges de signes contraires s'attirent proportionnellement au produit de leurs charges et inversement proportionnellement au carré de leur distance ; les forces sont de valeurs égales et de sens opposés, conformément au principe de l'action et de la réaction.

Comme en gravitation, l'action à distance se fait par l'intermédiaire d'un champ : le champ électrique :

Produit par 1 en 2 : 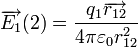$\overrightarrow{E_1}(2)= \frac{q_1\overrightarrow{r_{12}}}{4 \pi \varepsilon_0 r_{12}^2}$ produit par 2 en 1 : $\overrightarrow{E_2}(1)= \frac{q_2\overrightarrow{r_{21}}}{4 \pi \varepsilon_0 r_{21}^2}$

Le champ créé en M par n charges q_i situées en des points P_i est additif (principe de superposition). Dans le cas d'une distribution de charges discrète :

\overrightarrow{E_T}= \overrightarrow{E_1} + \overrightarrow{E_2} + \overrightarrow{E_3} + \ldots + \overrightarrow{E_n}=\overrightarrow{E_T}(M)= \sum_{i=1}^n \frac{q_i}{4\pi\varepsilon_0 }\frac{\overrightarrow{P_iM}} {\|\overrightarrow{P_iM}\|^3}

Dans le cas d'une distribution ρ de charges continue dans l'espace, le champ causé par un petit volume chargé vaut :

d\vec{E}(x_m,y_m,z_m) = \frac{\rho(x_i,y_i,z_i)}{4 \pi \varepsilon_0} \frac{\overrightarrow{r_{im}}}{r_{im}^3}\,dx_idy_idz_i

et en intégrant sur tout l'espace où il y a des charges, on obtient:

\vec{E}(x_m,y_m,z_m) = \iiint \frac{\rho(x_i,y_i,z_i)}{4 \pi \varepsilon_0} \frac{\overrightarrow{r_{im}}}{r_{im}^3}\,dx_idy_idz_i

où ρ est la densité volumique de charge en P_i, ^{$\overrightarrow{r_{im}}$} est le vecteur allant de P_i au point M. Dans l'élément de volume dx_i dy_i dz_i autour du point P_i il y a un élément de charge ρ(x_i, y_i, z_i)dx_i dy_i dz_i. Les intégrales indiquent qu'il faut additionner, d'après le principe de superposition, sur tous les volumes contenant des charges.

Le potentiel électrique (dont les différences s'appellent tensions) est une notion courante et importante de l'électrostatique : c'est une fonction scalaire dans l'espace, dont le champ électrique est le gradient,géométriquement si l'un des points d'un espace de coordonnées formant un n-uplet le gradient donne le vecteur le plus raide qui lierait deux points de cet espace.

V(x_m,y_m,z_m) = \iiint\frac{\rho(x_i,y_i,z_i)}{4 \pi \varepsilon_0|r_{im}|}\,dx_idy_idz_i

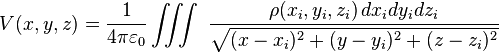V(x,y,z) = \frac{1}{4 \pi \varepsilon_0}\iiint\,\,\frac{\rho(x_i,y_i,z_i)\,dx_idy_idz_i }{\sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2}}

et en calculant les dérivées partielles

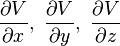
\frac{\partial V}{\partial x},~\frac{\partial V}{\partial y},~\frac{\partial V}{\partial z}

\vec{E}(x,y,z) = \frac{1}{4 \pi \varepsilon_0}\iiint\!\!\rho(x_i,y_i,z_i)\,\frac{ (x-x_i)\vec{e_x}+(y-y_i)\vec{e_y}+(z-z_i)\vec{e_z}} {[(x-x_i)^2+(y-y_i)^2+(z-z_i)^2]^{3/2}}\,dx_idy_idz_i

Toute l'électrostatique dans un milieu homogène est dans ces dernières formules, quoiqu'il faille remarquer que ces formules ne sont pas définies si le point de coordonnées (x_i, y_i, z_i) porte une charge ponctuelle, ce qui n'est d'ailleurs qu'une approximation non-physique (ρ devrait y être infini).

Les formules ci-haut se simplifient selon les invariances du champ électrostatique. Il est donc crucial d'étudier les symétries pour réduire le nombre de variables ; voir la partie autour des invariances.

Potentiel en 1/r et champ à divergence nulle

On place la charge qui produit le potentiel en O et on regarde alors le potentiel produit en M et son gradient. Dans ce paragraphe, il est supposé que O et M ne sont pas confondus ; sinon les formules n'auraient aucun sens car ce serait équivalent à calculer le potentiel de O sur lui-même ce qui est absurde. Posons :
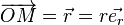
$\overrightarrow{OM}= \vec {r}= r \vec {e_r}$
Or, par définition des dérivées partielles :
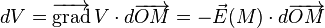
$dV=\overrightarrow{\mbox{grad}}\,V\cdot d \overrightarrow{OM}= - \vec{E}(M)\cdot d \overrightarrow{OM}$

sachant que l'on peut démontrer que 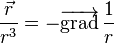$\frac{\vec{r}}{r^3}=-\overrightarrow{\mbox{grad}}\,\frac{1}{r}$ ¹, on en déduit en multipliant par 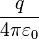$\frac{q}{4 \pi \varepsilon_0 }$ que :

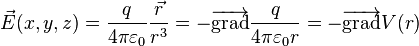\vec{E}(x,y,z)=\frac{q}{4 \pi \varepsilon_0 } \frac{\vec{r}}{r^3}= -\overrightarrow{\mbox{grad}} \frac{q}{4 \pi \varepsilon_0 r}= -\overrightarrow{\mbox{grad}} V(r)

avec

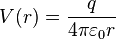
V(r)= \frac{q}{4 \pi \varepsilon_0 r}

les champs en 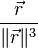$\frac{\vec{r}}{\|\vec{r}\|^3}$ sont tels que leur divergence est nulle : 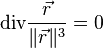$\mbox{div} \frac{\vec{r}}{\|\vec{r}\|^3} = 0$ ²

Théorème de Gauss

Le théorème de flux-divergence est un théorème d'analyse vectorielle, utilisable en électrostatique pour obtenir une équation locale du champ électrique.

Ce théorème indique que la somme des contributions vectorielles normales à des surfaces infinitésimales sur le bord d'un volume peut également s'exprimer comme une somme de surfaces infinitésimales coupant le volume, puisque les contributions des faces situées à l'intérieur se compensent exactement ; il s'écrit formellement :

\iiint_{v} \mbox{div} \vec E \ dv = \iint_{S} \vec E \cdot d \vec S

pour n'importe quel volume. En particulier, dans une sphère chargée en volume par une densité volumique de charge ρ, ayant son centre en O et de rayon r suffisamment petit pour qu'on puisse négliger les variations de ρ, avec $\vec{dS}=dS\vec{e_r}$ le vecteur normal à la surface dirigé vers l'extérieur, et de longueur égale à l'élément de surface dS qu'il représente :

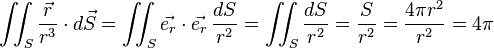
\iint_{S} \frac{\vec{r}}{r^3} \cdot d \vec S = \iint_{S}\vec{e_r}\cdot \vec{e_r}\,\frac{dS}{r^2} = \iint_{S}\frac{dS}{r^2} = \frac{S}{r^2} = \frac{4\pi r^2 }{r^2} = 4\pi

Ce qui signifie que le résultat ne dépend pas de r. Et si on multiplie par 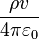$\frac{\rho v}{4 \pi \varepsilon_0 }$ où v est le volume de la sphère, on obtient :

\frac{\rho v}{4 \pi \varepsilon_0 }\iint_{S} \frac{\vec{r}}{r^3} \cdot d \vec S =\iint_{S} \frac{\rho v}{4 \pi \varepsilon_0 }\frac{\vec{r}}{r^3} \cdot d \vec S = \iint_{S} \vec{E} \cdot d \vec S = \frac{\rho v}{4 \pi \varepsilon_0 }\,4\pi = \frac{q}{ \varepsilon_0 }

où q est la charge totale ρv de la sphère. Soit finalement :

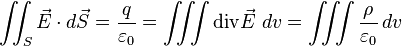
\iint_{S} \vec{E}\cdot d\vec S =\frac{q}{\varepsilon_0 }=\iiint\mbox{div} \vec E \ dv = \iiint\frac{\rho}{ \varepsilon_0 }\, dv

D'où le théorème de Gauss sous sa version locale :

\mbox{div} \vec E = \frac{\rho}{ \varepsilon_0 }

et l'expression intégrée, connue par les physiciens sous le nom de théorème de Gauss :

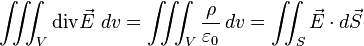\iiint_{V} \mbox{div} \vec E \ dv =\iiint_{V} \frac{\rho}{ \varepsilon_0 }\, dv =\iint_{S} \vec E \cdot d \vec S

L'équation de Poisson

L'équation de Poisson combine les relations précédentes pour donner une relation locale entre la distribution de charge et le potentiel :

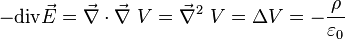-\mbox{div} \vec E = \vec {\nabla}\cdot \vec {\nabla}~ V = {\vec {\nabla}}^2~ V = \Delta V =-{\rho \over \varepsilon_0}

Voir l'article Nabla pour la signification du symbole ^{$\vec {\nabla}$}

On retrouve le fait que les influences des différentes charges s'ajoutent linéairement, c'est-à-dire que pour connaître la force exercée sur une charge électrique par plusieurs autres charges, il suffit de calculer la force qu'exercerait chacune des charges prise isolément, et d'additionner les résultats : on retrouve bien le principe de superposition, autre manière d'exprimer la linéarité de la loi de Coulomb.

La loi de Coulomb est très proche de l'expression des forces gravitationnelles ; mais ces dernières sont (pour une particule donnée) beaucoup plus faibles. Pourtant, les forces électrostatiques ont peu d'effet à grande échelle, tandis que la gravitation explique le mouvement des astres.

Cela provient du fait qu'en moyenne, la matière contient autant de charges positives que de charges négatives et donc, au-delà de l'échelle des inhomogénéités, leurs influences se compensent. Pour la gravitation, au contraire, dont l'expression de la force a un signe opposé à celui de l'électrostatique, bien que les masses aient toutes le même signe positif, elles s’attirent toutes, au lieu de se repousser comme le font des charges électriques de même signe.

Champ électrique créé par quelques distributions de charges

Les champs électriques peuvent rarement être calculés analytiquement par le calcul direct de la dernière formule mais peuvent toujours être calculés numériquement, surtout avec les progrès de l'informatique.

Lorsqu'il existe des symétries, on peut souvent faire le calcul en appliquant le théorème de Gauss au champ électrique :

Le flux du champ électrique à travers une surface fermée S est proportionnel à la somme des charges qui sont à l'intérieur de cette surface.

\iint_S \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_0}

Voici quelques exemples de résultats de calcul pour des distributions de charges symétriques.

Fil rectiligne infini, pris suivant l'axe Oz de densité linéique de charge λ, à distance r du fil :

Pour un point M, le plan passant par M contenant l'axe Oz est un plan de symétrie, ainsi que celui passant par M et orthogonal à l'axe Oz ; on en déduit que le champ résultant n'a de composante que suivant :

$\vec{e_r} : \vec{E}(r,\theta,z)= E_r(r,\theta,z)\, \vec{e_r}$

Les invariances par translation suivant Oz et par rotation suivant θ permettent de déduire que E_r ne doit pas dépendre des variables z et θ et donc :
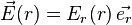
$\vec{E}(r)= E_r(r)\, \vec{e_r}$

Si pour appliquer le théorème de Gauss, on choisit un cylindre passant par M, d'axe Oz, de rayon r et d'épaisseur élémentaire dz :

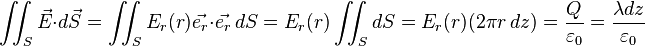
$\iint_S \vec{E} \cdot d\vec{S} = \iint_S E_r(r) \vec{e_r} \cdot \vec{e_r}\,dS =E_r(r)\iint_S dS = E_r(r) (2 \pi r \, dz) = \frac{Q}{\varepsilon_0} =\frac{\lambda dz}{\varepsilon_0}$

et on obtient finalement :

E_r(r)=\frac{\lambda}{2\pi\varepsilon_0}\frac{1}{r}

Plan infini, uniformément chargé en surface, de densité surfacique de charge σ, à distance r du plan. Comme le système est invariant par translation parallèle au plan, le champ ne peut être que perpendiculaire au plan. D'autre part, les champs sont directement opposés en deux points symétriques par rapport au plan. Si M est à la distance r du plan, considérons un prisme élémentaire symétrique par rapport au plan et dont une base, de surface dS, passe par M :

\iint_S \vec{E} \cdot d\vec{S}=2E(r) \, dS= \frac{\sigma\, dS}{\varepsilon_0}

d'où

E(r)=\frac{\sigma}{2\varepsilon_0}

La valeur absolue du champ est constante dans tout l'espace. Son sens change entre les deux côtés du plan ; il est donc discontinu au niveau du plan.

Sphère creuse de diamètre R, uniformément chargée en surface, de densité surfacique de charge σ, à distance r du centre :
- à l'intérieur (r < R) : $E(r) = 0 \quad$
- juste à l'extérieur de la surface (r = R+0) : $E(r) = \frac{\sigma}{\varepsilon_0}$ . À nouveau, le champ est discontinu au niveau d'une surface chargée.
- à l'extérieur (r > R) : $E(r) = \frac{\sigma}{\varepsilon_0}\frac{R^2}{r^2}$

Sphère pleine de diamètre R, uniformément chargée en volume, de densité volumique de charge ρ, à distance r du centre :
- à l'intérieur (r < R) : $E(r) = \frac{\rho}{3\varepsilon_0}r$
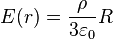
- à la surface (r = R) : $E(r) = \frac{\rho}{3\varepsilon_0}R$
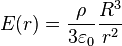
- à l'extérieur (r > R) : $E(r) = \frac{\rho}{3\varepsilon_0}\frac{R^3}{r^2}$

Conséquence du théorème de Gauss, nous retrouvons dans les deux cas à l'extérieur de la sphère un champ égal à celui d'une charge Q ponctuelle placée au centre de la sphère :

E(r) = 4\pi \sigma R^2\frac{1}{4\pi\varepsilon_0 r^2}=\frac{Q}{4\pi\varepsilon_0 r^2}

respectivement :

E(r) = \frac{4\pi \rho R^3}{3}\frac{1}{4\pi\varepsilon_0 r^2}=\frac{Q}{4\pi\varepsilon_0 r^2}

Exemples de potentiels

Potentiel d'un fil fini (-a, a) en b dans son prolongement :

V(b)=\int_{-a}^a\, \frac{\lambda}{4\pi\varepsilon_0} \frac{dx}{b-x}= \frac{\lambda}{4\pi\varepsilon_0}\,\ln\,\frac{b+a}{b-a}

Potentiel d'un disque chargé de rayon R à une distance z de son centre le long de son axe :

V(z)=\frac{\sigma}{4\pi\varepsilon_0}\int_0^R\frac{2\pi r\,dr}{\sqrt{r^2+z^2}}=\frac{\sigma}{2\varepsilon_0}\left(\sqrt{R^2+z^2}-z\right)

Un fil fini : calcul direct du champ produit

Supposons que l'on ait l'axe des x chargé sur un segment AB avec une densité de charge linéique constante λ et, un point M (x_M, y_M) dans le plan xOy où l'on veut déterminer le champ produit par les charges réparties sur AB.

Considérons le point P(x, 0). Il est dans un intervalle dx de AB ayant une charge λdx. Ces charges créent en M un champ. Posons PM = r :

\vec {E}(M)=\int_a^b\!\! d\vec{E}(M)=\frac{\lambda}{4\pi\varepsilon_0}\int_a^b \!\!\frac{\overrightarrow{PM}}{r^3} dx =\frac{\lambda}{4\pi\varepsilon_0}\int_a^b\!\!\left(\frac{(x_M-x)\vec {i}+y_M\vec {j}}{r^3}\right) dx

=\left(\frac{\lambda}{4\pi\varepsilon_0}\int_a^b\frac{(x_M-x)}{r^3}\right) dx \, \vec {i}+ \left(\frac{\lambda}{4\pi\varepsilon_0}\int_a^b\frac{y_M}{r^3} \right) dx \,\vec {j}

Il reste à faire les deux intégrales sur x pour obtenir les composantes de :

\vec {E}(x_M,y_M)= E_x(x_M,y_M)\,\vec {i}+ E_y(x_M,y_M)\,\vec {j}

En constatant que :

\frac{(x_M-x)}{r} = \sin\alpha

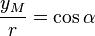\frac{y_M}{r} = \cos\alpha

on déduit :

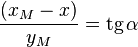\frac{(x_M-x)}{y_M} = \mbox{tg}\,\alpha

où α est le complémentaire de l'angle BPM,

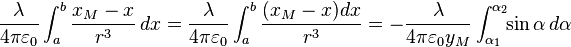\frac{\lambda}{4\pi\varepsilon_0}\int_a^b\frac{x_M-x}{r^3}\,dx =\frac{\lambda}{4\pi\varepsilon_0}\int_a^b\frac{(x_M-x)dx}{r^{3}} = - \frac{\lambda}{4\pi\varepsilon_0 y_M}\int_{\alpha_1}^{\alpha_2}\!\! \sin\alpha\,d\alpha

facile à intégrer

On a utilisé :
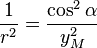$dx=\frac{-y_M}{\cos^2\alpha}\,d\alpha$ , $\frac{1}{r^2}=\frac{\cos^2\alpha}{y_M^2}$ et $\frac{x_M-x}{r}=\sin\alpha$

Distributions ayant des symétries et des invariances

Lorsqu'on se propose de calculer le champ électrostatique en un point distant d'un volume chargé on observe la morphologie du corps chargé, c'est comme si on avait une vision d'ensemble de celui-ci à partir de ce point, car les électrons libres ont un mouvement brownien et très rapide donc on peut négliger les zones d'ombre électroniques. À partir de là il suffit de considérer les propriétés géométriques de ce corps, ce qui est simple et très simplificateur des calculs. Pour une distribution de charge ayant une symétrie par rapport à un plan, il est facile de déduire que pour un point M du plan de symétrie, le champ résultant E(M) n'a de composantes que dans le plan de symétrie (la composante perpendiculaire au plan de symétrie s'annule : en regroupant les charges par paires symétriques en effet, on constate cette nullité).

Exemple: Si on a une distribution sphérique de charge de centre O, alors tout plan passant par O est un plan de symétrie : en conséquence, le champ résultant en M est dans tous les plans contenant OM et donc 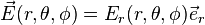^{$\vec E (r,\theta, \phi)= E_r(r,\theta, \phi) \vec e_r$} puisque E_θ(r, θ, φ) = 0 et E_φ(r, θ, φ) = 0.

Plus généralement, si, pour une transformation euclidienne T, la distribution ρ(T(M)) est identique à ρ(M), le champ en T(M) sera le transformé par T de celui en M. On dit que la distribution est invariante par la transformation T.

C'est le cas, pour une distribution sphérique, par toute rotation autour du centre et on en déduit que le champ est purement radial, et sa valeur mesurée le long du rayon ne dépend que de sa distance au centre. En coordonnées polaires :

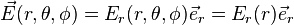
\vec E (r,\theta, \phi)= E_r(r,\theta, \phi) \vec e_r =E_r(r) \vec e_r

Ce résultat simplifie beaucoup les calculs.

Autre exemple : cas d'une symétrie cylindrique, avec invariance de ρ par symétrie par rapport à tout plan contenant Oz, ou perpendiculaire à Oz, on obtient :

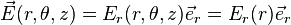
\vec E (r,\theta, z)= E_r(r,\theta, z) \vec e_r =E_r(r) \vec e_r

Électricité statique : risques, applications et contraintes

La production d'électricité statique peut être non souhaitée voire contraignante dans le cadre de productions industrielles car pouvant conduire au mauvais fonctionnement, à la détérioration d'équipements sur le long terme, ou, dans les cas à risque, par explosions.

Des « décharges électriques » par frottements de tissus, ou autres sont l'une des premières sources d'inflammation en zone à risque d’explosion (atmosphères explosibles : ATEX), notamment dans des secteurs tels que agro-alimentaire, chimie, parachimie, pharmacie, industrie du bois, sidérurgie, pyrotechnie...
Des méthodes et essais d'évaluation du risque et de certification volontaire^[1] ont été développés et sont encore en développement, de même des matériaux antistatiques, notamment sous l'égide de l'INERIS en France^[2].

Dans le domaine de la santé, l'électricité statique, par exemple par l'utilisation prolongée des anciens écrans d'ordinateurs, peut causer du stress, une augmentation artérielle ou le déclenchement de crampes nocturnes (comme le chercheur et médecin italien Luigi Galvani l'avait déjà compris au XVIIe siècle).

Voir aussi

Liens externes

une vidéo explicative sur les lignes de champ électrostatique

Bibliographie

Expérience, au Palais de la découverte à Paris

Ouvrage d'introduction

Richard P. Feynman, Robert B. Leighton (en) et Matthew Sands (en), Le Cours de physique de Feynman [détail de l’édition], InterEditions (1979)

Accessible dès le premier cycle universitaire. Le grand théoricien de l'électrodynamique quantique, prix Nobel de physique 1965, nous donne ici un superbe cours d'introduction à l'électromagnétisme classique. L'électrostatique est traitée dans le premier volume : Électromagnétisme I (ISBN 2-7296-0028-0). Rééd. Dunod (ISBN 2-10-004861-9)

Ouvrages de référence

Émile Durand ; Électrostatique, Masson (1953). Un traité monumental en trois volumes :
- Vol 1 : Distributions
- Vol 2 : Problèmes généraux & conducteurs
- Vol 3 : Méthodes de calcul
John David Jackson (trad. de l'anglais), Électrodynamique classique [« Classical Electrodynamics »] [détail de l’édition]
(en) Wolfgang K. H. Panofsky et Melba Phillips ; Classical electricity and magnetism, Addison-Wesley (2^e édition-1962). Réédité par : Dover Publications, Inc. (2005), (ISBN 0486439240). L'ouvrage de référence en électrodynamique classique avant la parution du Jackson

Références

↑ Ineris, nouveau référentiel et schéma de certification volontaire Electrostatic-INERIS ; Lettre numéro 23, août 2012, 4 pp
↑ Electricité statique : source d’incendie et d’explosion L’INERIS propose une réponse adaptée aux industriels, juin 2010

Portail de la physique
Portail de l’électricité et de l’électronique

This article is issued from Wikipédia - version of the Friday, September 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.