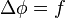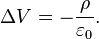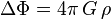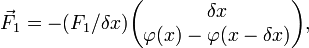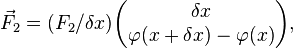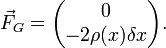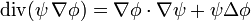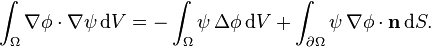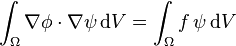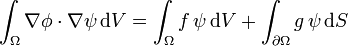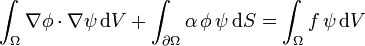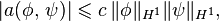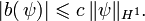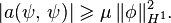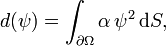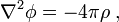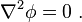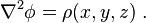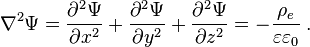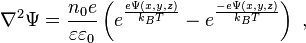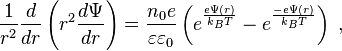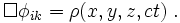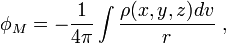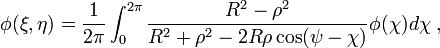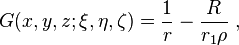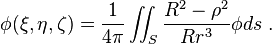Équation de Poisson

Pour les articles homonymes, voir Poisson (homonymie).

En analyse vectorielle, l'équation de Poisson (ainsi nommée en l'honneur du mathématicien et physicien français Siméon Denis Poisson) est l'équation aux dérivées partielles du second ordre suivante :

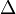\displaystyle \Delta\phi=f

où $\displaystyle \Delta$ est l'opérateur laplacien et 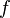$\displaystyle f$ est une fonction généralement donnée.

Sur un domaine borné de 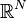$\R^N$ et de frontière régulière, le problème de trouver 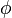$\displaystyle \phi$ à partir de 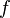$\displaystyle f$ et satisfaisant certaines conditions aux limites appropriées est un problème bien posé : la solution existe et est unique.

Ce problème est important en pratique :

En électrostatique, la formulation classique (voir Équation de Poisson-Boltzmann) exprime le potentiel électrique 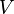$\displaystyle V$ associé à une distribution connue de charges 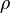$\displaystyle \rho$ par la relation

\Delta V = - {\rho \over \varepsilon_0}.

En gravitation universelle, le potentiel gravitationnel 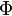$\displaystyle \Phi$ est relié à la masse volumique 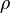$\displaystyle \rho$ par la relation

\displaystyle\Delta \Phi = 4 \pi \, G \, \rho

Conditions aux limites

L'équation de Poisson étant insensible à l’ajout sur 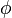$\displaystyle \phi$ d’une fonction satisfaisant l’équation de Laplace (ou une simple fonction linéaire par exemple), une condition aux limites est nécessaire pour espérer l'unicité de la solution : par exemple les conditions de Dirichlet, celles de Neumann, ou des conditions mixtes sur des portions de frontière.

Équation de Poisson à deux dimensions

En coordonnées cartésiennes dans 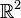$\mathbb R^2$ , considérons un ouvert 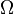$\displaystyle \Omega$ , une fonction 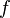$\displaystyle f$ continue sur 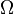$\displaystyle \Omega$ et une fonction 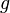$\displaystyle g$ continue sur la frontière 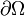$\partial \Omega$ . Le problème consiste à trouver une fonction de deux variables réelles 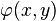$\varphi(x,y)$ définie sur 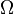$\displaystyle \Omega$ qui vérifie les deux relations :

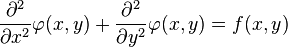{\partial^2 \over \partial x^2 }\varphi(x,y) + {\partial^2 \over \partial y^2 }\varphi(x,y) = f(x,y)

sur

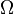\displaystyle \Omega

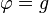\varphi = g

sur

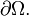
\partial \Omega.

Cette formulation est un modèle mathématique du problème statique d’une membrane élastique tendue et chargée (une peau de tambour) :

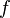$\displaystyle f$ est la densité de charge (exprimée par exemple en Pa, ceci à un multiple près caractérisant les propriétés d’élasticité de la membrane) ;
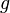$\displaystyle g$ est la cote (élévation verticale) le long de la frontière de fixation de la membrane ;
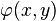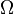la solution $\varphi(x,y)$ indique la cote de la membrane dans $\displaystyle \Omega$ .

Éléments de justification

À une dimension, il s’agit d’une corde élastique chargée qui est fixée en ses deux extrémités.

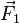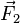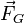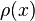Sur un petit élément $\displaystyle [x - \delta x, x + \delta x]$ , considérons l’équilibre statique entre les deux forces de traction $\vec F_1$ et $\vec F_2$ de la corde (respectivement à gauche et à droite), puis la force de la charge $\vec F_G$ induite par une densité de charge linéaire notée $\displaystyle \rho(x)$ :

$\vec F_1 = - (F_1 / \delta x) \begin{pmatrix} \delta x \\ \varphi(x) - \varphi(x - \delta x) \end{pmatrix},$
$\vec F_2 = (F_2 / \delta x) \begin{pmatrix} \delta x \\ \varphi(x + \delta x) - \varphi(x) \end{pmatrix},$
$\vec F_G = \begin{pmatrix} 0 \\ - 2 \rho(x) \delta x \end{pmatrix}.$

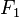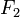Sans restreindre la généralité, les facteurs $\displaystyle F_1$ et $\displaystyle F_2$ ont été divisés par 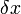$\displaystyle \delta x$ afin de leur conserver une grandeur non différentielle.

La somme vectorielle de ces forces conduit aux égalités :

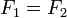$\displaystyle F_1 = F_2$ qu’on peut appeler 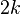$2 \displaystyle k$ , un coefficient indépendant de 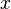$\displaystyle x$ puisque toutes les composantes horizontales se compensent pour se répercuter uniquement sur les points d’attache,
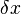${2 k \over \delta x} [\varphi(x + \delta x) - 2 \varphi(x) + \varphi(x - \delta x)] = 2 \rho(x) \delta x$ qui, lorsque $\delta x$ tend vers 0, s’écrit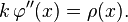 $k \, \varphi ''(x) = \rho(x).$

Cette dernière relation est bien l’équation de Poisson à une dimension.

Formulation faible et solution

Soit 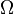$\displaystyle \Omega$ un domaine ouvert et borné de 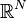$\R^N$ dont la frontière 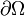$\part \Omega$ est suffisamment régulière pour satisfaire le théorème de la divergence. Soit 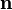$\mathbf n$ le vecteur normal à 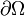$\part \Omega$ et dirigé vers l’extérieur.

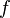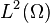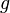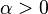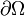Soient $\displaystyle f$ une fonction de $\displaystyle L^2(\Omega)$ , puis $\displaystyle g$ et $\alpha > 0$ des fonctions continues définies sur $\part \Omega$ .

On cherche une solution 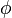$\displaystyle \phi$ pour chacun des problèmes suivants :

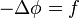\displaystyle - \Delta\phi=f

sur

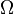
\displaystyle \Omega

satisfaisant l’une des conditions sur

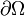\part \Omega

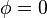
$\displaystyle \phi = 0$
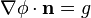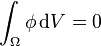$\nabla \phi \cdot \mathbf n = g$ et $\int_{\Omega} \phi \, \mathrm{d}V = 0$ (pour fixer la constante additive d’indétermination)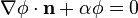
$\nabla \phi \cdot \mathbf n + \alpha \phi = 0$

Pour toute fonction 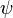$\displaystyle \psi$ régulière, la relation

{\mathrm{div}} (\psi \, \nabla \phi) = \nabla \phi \cdot \nabla \psi + \psi \Delta\phi

et le théorème de la divergence impliquent

\int_{\Omega} \nabla \phi \cdot \nabla \psi \, \mathrm{d}V = - \int_{\Omega} \psi \, \Delta\phi \, \mathrm{d}V + \int_{\part\Omega} \psi \, \nabla \phi \cdot \mathbf n \, \mathrm{d}S.

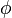Si $\displaystyle \phi$ est solution du problème précédent muni de la condition aux limites retenue, alors

$\int_{\Omega} \nabla \phi \cdot \nabla \psi \, \mathrm{d}V = \int_{\Omega} f \, \psi \, \mathrm{d}V$
$\int_{\Omega} \nabla \phi \cdot \nabla \psi \, \mathrm{d}V = \int_{\Omega} f \, \psi \, \mathrm{d}V + \int_{\part\Omega} g \, \psi \, \mathrm{d}S$
$\int_{\Omega} \nabla \phi \cdot \nabla \psi \, \mathrm{d}V + \int_{\part\Omega} \alpha \, \phi \, \psi \, \mathrm{d}S = \int_{\Omega} f \, \psi \, \mathrm{d}V$

En notant 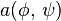$a(\phi, \, \psi)$ le membre de gauche et 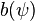$\displaystyle b(\psi)$ celui de droite, la formulation faible consiste à :

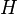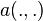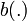définir un espace vectoriel $\displaystyle H$ approprié dans lequel $\displaystyle a(.,.)$ et $\displaystyle b(.)$ sont définies,
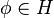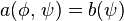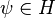rechercher $\displaystyle \phi \in H$ tel que $a(\phi, \, \psi) = b(\psi)$ pour tout $\psi \in H$ .

Si elle existe, la solution naturelle de ces formulations se trouve dans l’espace de Sobolev 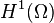$\displaystyle H^1(\Omega)$ muni de sa norme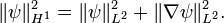 $\|\psi\|^2_{H^1} = \|\psi\|^2_{L^2} + \|\nabla \psi\|^2_{L^2}.$

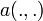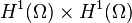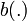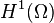En effet, pour chaque problème, $a(., .)$ est une forme bilinéaire symétrique définie sur $H^1(\Omega) \times H^1(\Omega)$ , et $b(.)$ est une forme linéaire sur $\displaystyle H^1(\Omega)$ .

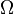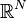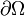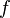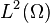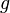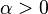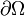Proposition — Soit $\displaystyle \Omega$ un domaine ouvert et borné de $\R^N$ et de frontière $\part \Omega$ régulière (ou régulière par morceaux), $\displaystyle f$ dans $\displaystyle L^2(\Omega)$ , puis $\displaystyle g$ et $\alpha > 0$ des fonctions continues définies sur $\part \Omega$ .

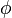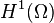Alors les trois problèmes précédents possèdent une unique solution $\displaystyle \phi$ dans $\displaystyle H^1(\Omega)$ qui est caractérisée par la formulation faible correspondante mise en œuvre dans les espaces suivants :

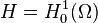$H = H^1_0(\Omega)$ qui est l’adhérence dans 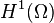$\displaystyle H^1(\Omega)$ des fonctions indéfiniment dérivables et à support compact dans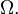 $\displaystyle \Omega.$
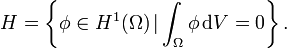
$H = \left \{ \phi \in H^1(\Omega) \, | \int_{\Omega} \phi \, \mathrm{d}V = 0 \right \}.$
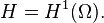
$\displaystyle H = H^1(\Omega).$

Justification

Si les conditions de continuité et de coercivité des hypothèses du théorème de Lax-Milgram sont satisfaites, ce dernier permet de conclure.

Continuité

Pour la continuité des deux formes, il s’agit de montrer l’existence de constantes positives notées génériquement $\displaystyle c$ telles que

|a(\phi, \, \psi)| \leqslant c \, \|\phi\|_{H^1} \|\psi\|_{H^1},

|b(\, \psi)| \leqslant c \, \|\psi\|_{H^1}.

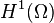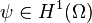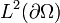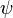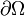Ces constantes existent par définition de la norme de $\displaystyle H^1(\Omega)$ et par la continuité des opérateurs de trace qui, à une fonction $\psi \in H^1(\Omega)$ associe un fonction de $L^2(\part \Omega)$ définie par la restriction de $\displaystyle \psi$ sur $\part \Omega$ .

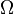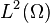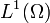On peut remarquer que la continuité des formes assure simultanément leur définition rigoureuse. Pour le second problème en particulier, $\displaystyle \Omega$ borné implique la continuité de l’injection de $\displaystyle L^2(\Omega)$ dans $\displaystyle L^1(\Omega)$ pour la norme 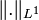$\|.\|_{L^1}$ , ce qui justifie la définition de l’espace 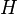$\displaystyle H$ correspondant.

Coercivité

Pour la coercivité des 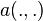$\displaystyle a(.,.)$ , il s’agit de montrer l’existence d’une constante 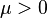$\displaystyle \mu > 0$ indépendante de 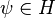$\psi \in H$ telle que

$|a(\psi, \, \psi)| \geqslant \mu \, \|\phi\|^2_{H^1}.$

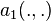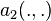Cette propriété découle de l’inégalité de Poincaré classique pour la forme $\displaystyle a_1(.,.)$ et de l’inégalité de Poincaré-Wirtinger pour la forme $\displaystyle a_2(.,.)$ .

La coercivité de la forme 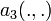$\displaystyle a_3(.,.)$ peut se montrer par l’absurde. En notant

d(\psi) = \int_{\part\Omega} \alpha \, \psi^2 \, \mathrm{d}S,

supposons qu’il existe une suite 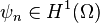$\psi_n \in H^1(\Omega)$ satisfaisant

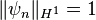\|\psi_n\|_{H^1} = 1

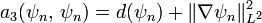a_3(\psi_n, \, \psi_n) = d(\psi_n) + \|\nabla \psi_n\|^2_{L^2}

tend vers 0.

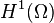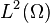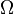Par compacité de l’injection canonique de $\displaystyle H^1(\Omega)$ dans $\displaystyle L^2(\Omega)$ (lorsque $\displaystyle \Omega$ est borné), il existe une sous-suite convergeant vers une fonction 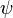$\displaystyle \psi$ pour la norme 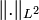$\|.\|_{L^2}$ . Cette suite est donc une suite de Cauchy dans 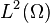$\displaystyle L^2(\Omega)$ et, puisque son gradient tends vers 0 dans 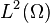$\displaystyle L^2(\Omega)$ , elle est également une suite de Cauchy dans 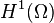$\displaystyle H^1(\Omega)$ qui converge vers 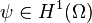$\psi \in H^1(\Omega)$ et qui ne peut être qu’une fonction constante avec 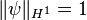$\|\psi\|_{H^1} = 1$ . 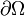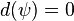Ainsi, sa trace sur $\part \Omega$ (par continuité) ne peut être que constante non nulle, ce qui contredit $d(\psi)=0$ .

Résolution

Il y a diverses méthodes pour la résolution numérique. La méthode de relaxation, un algorithme itératif, est un exemple. Les méthodes basées sur les transformées de Fourier sont presque toujours utilisées en gravitation universelle.

Considérations historiques et essais de résolution

L'équation de Poisson est une correction célèbre de l’équation différentielle de Laplace au second degré pour le potentiel :

\nabla^2 \phi = - 4 \pi \rho \; ,

On appelle aussi cette équation : l'équation de la théorie du potentiel publiée en 1813. Si une fonction d’un point donné ρ = 0, nous obtenons l’équation de Laplace :

\nabla^2 \phi = 0 \; .

En 1812, Poisson découvrit que cette équation n’est valide qu'hors d’un solide. Une preuve rigoureuse pour les masses avec une densité variable fut d’abord donnée par Carl Friedrich Gauss en 1839. Les deux équations ont leurs équivalents en analyse vectorielle. L’étude des champs scalaires φ d’une divergence^[Quoi ?] donne :

\nabla^2 \phi = \rho (x, y, z) \; .

Par exemple, une équation de Poisson pour un potentiel électrique en surface Ψ, qui montre sa dépendance de la densité d’une charge électrique ρ_e dans une place particulière :

\nabla^2 \Psi = {\partial ^2 \Psi\over \partial x^2 } + {\partial ^2 \Psi\over \partial y^2 } + {\partial ^2 \Psi\over \partial z^2 } = - {\rho_{e} \over \varepsilon \varepsilon_{0}} \; .

La distribution d’une charge dans un fluide est inconnue et nous devons utiliser l’équation de Poisson-Boltzmann :

\nabla^2 \Psi = {n_{0} e \over \varepsilon \varepsilon_{0}} \left( e^{e\Psi (x,y,z)\over k_{B}T} - e^{-e\Psi (x,y,z)\over k_{B}T} \right) \; ,

ce qui, dans la plupart des cas, ne peut être résolu analytiquement, mais seulement pour des situations particulières. Dans les coordonnées polaires, l’équation de Poisson-Boltzmann est :

{1\over r^{2}} {d\over dr} \left( r^{2} {d\Psi \over dr} \right) = {n_{0} e \over \varepsilon \varepsilon_{0}} \left( e^{e\Psi (r)\over k_{B}T} - e^{-e\Psi (r)\over k_{B}T} \right) \; ,

laquelle ne peut pas non plus être résolue analytiquement. Même si le champ φ n’est pas scalaire, l’équation de Poisson est valide, comme elle peut l’être par exemple dans un espace de Minkowski à quatre dimensions :

\square \phi_{ik} = \rho (x, y, z, ct) \; .

Si ρ(x, y, z) est une fonction continue et si pour r→∞ (ou si un point 'se déplace' à l’infini) une fonction φ va à 0 suffisamment rapidement, une solution à l’équation de Poisson est le potentiel newtonien d’une fonction ρ(x, y, z) :

\phi_M = - {1\over 4 \pi} \int {\rho (x, y, z) dv \over r} \; ,

où r est une distance entre l’élément avec le volume dv et le point M. L’intégration parcourt la totalité de l’espace. L’intégrale de Poisson en résolvant la fonction de Green pour le Problème de Dirichlet de l’équation de Laplace, si le cercle est le domaine étudié :

\phi(\xi , \eta) = {1\over 2 \pi} \int _0^{2\pi} {R^2 - \rho^2\over R^2 + \rho^2 - 2R \rho \cos (\psi - \chi) } \phi (\chi) d \chi \; ,

où :

\xi = \rho \cos \psi \; , \quad \eta = \rho \sin \psi \; .

φ(χ) est une fonction prescrite sur une ligne circulaire, qui définit les conditions aux limites de la fonction requise φ de l’équation de Laplace. De la même manière nous définissons la fonction de Green pour le problème de Dirichlet pour l’équation de Laplace ² φ = 0 dans l’espace, pour un domaine constitué d’une sphère de rayon R. Cette fois la fonction de Green est:

G(x,y,z;\xi,\eta,\zeta) = {1\over r} - {R\over r_1 \rho} \; ,

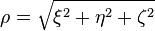où : $\rho = \sqrt {\xi^2 + \eta^2 + \zeta^2}$ est une distance d’un point (ξ, η, ζ) depuis le centre d’une sphère, r une distance entre des points (x, y, z), (ξ, η, ζ), r₁ est une distance entre le point (x, y, z) et le point (Rξ/ρ, Rη/ρ, Rζ/ρ), symétrique au point (ξ, η, ζ). L’intégrale de Poisson est maintenant de la forme:

\phi(\xi, \eta, \zeta) = {1\over 4 \pi} \int\!\!\!\int_S {R^2 - \rho^2 \over R r^3} \phi ds \; .

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Siméon Denis Poisson » (voir la liste des auteurs).

Poisson Equation at EqWorld: The World of Mathematical Equations.
L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998. ISBN 0-8218-0772-2
A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9

Liens externes

(en) Eric W. Weisstein, « Poisson Integral », MathWorld
(en) Eric W. Weisstein, « Poisson Kernel », MathWorld
(en) Poisson's Integral for the Unit Disk

Portail de l’analyse
Portail de la physique

This article is issued from Wikipédia - version of the Tuesday, July 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.