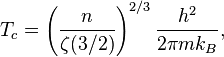Condensat de Bose-Einstein

Pour les articles homonymes, voir condensat.

Condensation de Bose-Einstein dans un gaz en fonction de la température, et diagramme en énergie

Un condensat de Bose-Einstein est un état de la matière apparent au niveau macroscopique, formé de bosons identiques (typiquement des atomes se comportant comme des bosons), tel qu'un grand nombre de ces particules, à une température suffisamment basse, occupent un unique état quantique de plus basse énergie (état fondamental) permettant des propriétés spécifiques.

Ce phénomène a été prédit en 1925 par Albert Einstein qui a généralisé au cas des atomes les travaux de Satyendranath Bose sur les statistiques quantiques des photons (travaux ouvrant la voie vers les lasers). En 1938, Pyotr Kapitsa, John Allen (en) et Don Misener découvrirent le caractère superfluide de l'hélium 4, pour des températures inférieures à 2,17 K. Cette propriété a rapidement été reliée à la condensation de Bose-Einstein d'une partie des atomes d'hélium 4, qui sont des bosons, par Fritz London. Le premier condensat gazeux a été produit en 1995 par Eric Cornell et Carl Wieman, ouvrant la voie à l'étude des gaz atomiques dilués ultrafroids dans le régime quantique et leur offrant le prix Nobel de physique en 2001.

Historique

Prédictions théoriques

La statistique quantique impliquée dans le phénomène de condensation de Bose-Einstein concerne les particules appartenant à la famille des bosons, qui sont les particules de spin entier, en opposition à la famille des fermions qui sont de spin demi-entier.

Satyendra Nath Bose proposa une statistique pour les photons différente de la statistique classique de Boltzmann, en se basant sur la possibilité pour plusieurs photons d'être dans le même état et sur l'indiscernabilité absolue de deux photons de même état quantique. Albert Einstein généralisa cette statistique à toutes les particules bosoniques, qu'elles soient non massives, comme le photon, ou massives, comme les atomes d'hélium 4.

L'étude par ce dernier du gaz parfait monoatomique bosonique a montré l'existence d'une transition de phase entre le gaz classique et un état de la matière où les atomes s'accumulent dans l'état quantique de plus basse énergie, lorsqu'on diminue la température. Cette phase est aujourd'hui appelée un condensat de Bose-Einstein. Le manuscrit d'Albert Einstein, titré Quantum theory of the monatomic ideal gas, daté de décembre 1924 a été découvert dans les archives de l'institut Lorenz de l'Université de Leyde^[1].

L'hélium superfluide

Après la découverte expérimentale de la superfluidité de l'hélium 4 liquide à basse température par Pyotr Kapitsa, John Allen et Don Misener, Fritz London proposa l’existence d’un lien entre ce phénomène et la condensation de Bose-Einstein. On a depuis découvert qu'à très basse température, environ 10 % des atomes occupent un même état quantique, formant effectivement un condensat. Cependant, de par les fortes interactions entre atomes d'hélium, la proportion d'atomes condensés reste faible, même à très basse température, alors que l'ensemble du fluide possède les propriétés superfluides. Il ne s'agit donc pas d'un cas stricto-sensu de condensat de Bose-Einstein, où l'on considère gaz dilué de bosons sans interactions, mais il s'agit bien d'un condensat dans lequel une forte interaction entre les bosons qui intervient doit être prise en compte dans la théorie.

Gaz atomiques dilués ultrafroids

Graphique 3D montrant 3 états successifs : les atomes sont de plus en plus denses (de la gauche vers la droite).

La physique de l'hélium 4 à très basse température est très complexe du fait des fortes interactions entre atomes. Afin de pouvoir étudier et exploiter plus simplement le phénomène de condensation de Bose-Einstein, on a cherché à l'observer pour des systèmes très dilués, plus proches du gaz parfait qui avait été le modèle initialement présenté par Einstein.

L'observation expérimentale des condensats a été possible grâce au développement des techniques de refroidissement d'atomes par laser. Les très basses températures atteintes ont permis d'atteindre le régime de condensation pour des gaz suffisamment dilués pour que les interactions ne masquent pas le phénomène de condensation. En 1995, une équipe du laboratoire NIST/JILA (Boulder, Colorado, États-Unis), dirigée par Eric Cornell et Carl Wieman, est parvenue à obtenir pendant quelques secondes un condensat de Bose-Einstein ; il était constitué de quelques milliers d’atomes de rubidium pré-refroidis par laser, puis refroidis plus avant par « évaporation » dans un piège magnétique. La température du gaz était alors de l'ordre de 100 nK.

Un troisième chercheur, Wolfgang Ketterle diplômé de l'université Ludwig-Maximilian de Munich, étudie également de son côté "le refroidissement par laser et le piégeage des atomes froids" ainsi que la superfluidité dans les gaz à « haute température ».

Ces trois chercheurs (Cornell, Wieman et Ketterle), recevront en 2001, le prix Nobel de physique "pour la découverte de la condensation de Bose-Einstein dans les gaz et pour des avancées dans l'étude des propriétés de ces condensats".

Condensation d'excitons

La condensation de Bose-Einstein a été obtenue en 2006 pour des excitons, quasi-particules composées d'un trou et d'un électron, dans la matière condensée. Elle fut réalisée hors équilibre thermodynamique et à beaucoup plus haute température, jusqu'à 20 K. Avec une fraction d'excitons condensés d'environ 50 %, ce système se situe entre l'hélium superfluide et les condensats atomiques.

Propriétés physiques

Gaz de Bose parfait

Einstein montra en 1925 que des bosons identiques, sans interaction entre eux, à l'équilibre thermodynamique, condensent dans un nouvel état de la matière à une température suffisamment basse. Cet état est aujourd'hui appelé condensat de Bose-Einstein ; il est caractérisé par une population macroscopique de l'état quantique de plus basse énergie. La température de changement d'état (température critique) est donnée par la relation

T_c=\left(\frac{n}{\zeta(3/2)}\right)^{2/3}\frac{h^2}{2\pi m k_B},

où

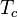$T_c$ est la température de changement d'état,
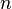$n$ la densité en bosons,
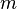$m$ la masse d'un boson,
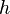$h$ la constante de Planck,
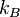$k_B$ la constante de Boltzmann et
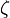$\zeta$ la fonction zêta de Riemann : ζ (3/2) ≈ 2,6124.

London remarqua que la température de la transition superfluide de l'hélium 4 (2,2 K) est du même ordre de grandeur que la température de condensation de Bose-Einstein d'un gaz parfait de même densité que l'hélium liquide (3,2 K), d'où son intuition que les deux phénomènes sont liés. L'hélium liquide superfluide est cependant très différent du modèle du gaz parfait.

Les condensats gazeux obtenus récemment sont environ mille milliards de fois plus dilués que l'hélium liquide (10¹⁵ atomes/m³ contre 10²⁷ atomes/m³); la température de condensation est alors de l'ordre du microkelvin.

Effet des interactions

Si la faiblesse des interactions explique le succès du modèle du gaz parfait pour prédire certaines propriétés des condensats gazeux, d'autres effets ne peuvent être compris qu'en tenant compte des interactions entre atomes, par exemple la taille du condensat piégé, sa superfluidité ou encore ses fréquences d'oscillation lorsqu'on le fait vibrer. Dans le cas d'un gaz dilué, l'équation de Gross-Pitaevskii permet de prendre en compte ces interactions.

Le phénomène de résonance de Feshbach permet d'ailleurs de changer la force des interactions en plongeant le condensat dans un champ magnétique. On peut ainsi étudier des situations où les atomes du condensat sont fortement corrélés. Ces études peuvent être utiles à la compréhension de phénomènes complexes de la physique de la matière condensée, comme la transition de Mott.

Interférences atomiques

Un condensat forme une onde de matière cohérente. Deux paquets d'onde issus du même condensat ou de deux condensats différents interfèrent lorsqu'ils se superposent, de manière analogue à la figure d'interférence des trous d'Young en optique (I.Bloch et al. Nature 403 166 2000).

Un nuage atomique ultra-froid piégé dans un réseau optique forme une série de condensats régulièrement espacés qui, lorsqu'ils interfèrent tous ensemble, peuvent former des figures d'interférences très piquées, tout comme la figure de diffraction d'une onde lumineuse par un réseau.

Condensat en rotation et vortex

La mise en rotation d'un condensat révèle de manière spectaculaire les contraintes qu'impose la mécanique quantique. Il est impossible de faire tourner un condensat en bloc, à l'image d'un objet classique. La mise en rotation s'accompagne de la création de vortex, c'est-à-dire de lignes le long desquelles la densité est nulle et autour desquelles la circulation de la vitesse est quantifiée. La première observation de vortex a été effectuée dans l'équipe de Jean Dalibard au laboratoire Kastler Brossel (Paris, France).

Applications

Scientifiques

Une application est la réalisation de lasers à atomes, c’est-à-dire d’instruments capables de délivrer un faisceau d’atomes se trouvant tous dans le même état, à l’instar des photons d’un rayon laser. Cela rendrait de grands services à l’optique et l’interférométrie atomiques, à la chimie (étude de réactions entre deux faisceaux atomiques dans des conditions très bien définies et contrôlées, condensats de molécules, etc.). Plusieurs équipes de physiciens sont parvenues, dès 1997, à produire un effet laser avec des atomes, le principe étant de former d’abord un condensat puis d’extraire par un moyen adéquat une partie des atomes condensés. Mais beaucoup de chemin reste à parcourir avant d’arriver à des flux atomiques d’intensité et de durée appréciables.

Industrielles

Une application pourrait se trouver dans la création de lasers à courte longueur d'onde (dans le champ des UV ou des rayons X). Cette application, envisagée par des chercheurs de l'université de Bonn après avoir obtenu un condensat de photons, pourrait notamment servir à la miniaturisation des circuits imprimés^[2].

Généralisation du concept de condensation

On considère habituellement qu'un condensat est caractérisé par une fraction macroscopique d'atomes dans le seul état fondamental. Cependant il a été montré expérimentalement, en particulier pour les atomes froids dans les pièges très anisotropes (systèmes à basses dimension) que la condensation peut avoir lieu sur plusieurs états quantiques proche de l'état fondamental, ce qui se caractérise notamment par une décroissance de la longueur de cohérence du condensat. On parle alors d'un condensat fragmenté. La Condensation de Bose-Einstein généralisée est une notion théorique permettant de décrire et de classifier les différents types de condensats possibles.

Notes et références

↑ Illustrations
↑ German physicists create a 'super-photon' sur physorg.com

Voir aussi

Liens externes

BEC 2009 Bose-Einstein Condensation 2009
Une conférence de Claude Cohen-Tannoudji sur la question
Une conférence de Sébastien Balibar sur la superfluidité
Conductivités et supraconductivité une conférence à l'UTLS de Jacques Lewiner
Une conférence de Jean Dalibard sur les condensats de Bose-Einstein
Observation d'un condensat de Bose-Einstein dans BaCuSi₂O₆ (M. Jaime et al. PRL 93 087203 2004)
Observation d'un condensat de Bose Eintein de polaritons dans une microcavité, Une conférence de Benoit Deveaud
Article de vulgarisation sur la condensation de Bose Einstein en phase solide
Un exemple de modélisation : le condensat de Bose-Einstein

Portail de la physique

This article is issued from Wikipédia - version of the Friday, January 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.