Mesure physique

La mesure physique est l'action de déterminer la ou les valeurs d'une grandeur (longueur, capacité, etc.), par comparaison avec une grandeur constante de même espèce prise comme terme de référence (étalon ou unité). Selon la définition canonique :

Mesurer une grandeur, c'est la comparer à une autre grandeur de même espèce prise comme unité.

La comparaison est quantitative ; on exprime la grandeur par un nombre rationnel multipliant l'unité. La mesure physique vise à une communication précise à propos d'un objet. Des unités communes à l'ensemble des mesures sont nécessaires ; faute de quoi, il faut établir des règles de conversion. Le Bureau international des poids et mesures a établi un Système International d'unités fondé sur un petit nombre d'étalons et des relations entre les unités.

À la différence d'un comptage, donnant une quantité entière définie par une réponse logique, une mesure physique est une estimation et possède donc une certaine incertitude.

En physique, la mesure physique se définit comme la détermination de la valeur numérique d'une grandeur par l'interprétation du résultat d'une expérience ou d'une observation. Les conditions et les méthodes de cette expérience ou observation déterminent l'incertitude^[1]. L'incertitude est partie intégrante de la mesure, et peut même être son résultat principal.

Généralités

En sciences naturelles, l'acte de mesurer un objet implique de comparer une caractéristique de l'objet avec une unité-étalon en utilisant un instrument dédié dans des conditions contrôlées. On pourra citer comme exemples d'instruments de mesure le thermomètre, le voltmètre, l'odomètre, le tachymètre, le dynamomètre, etc.. Afin d'effectuer une mesure physique avec précision, les instruments de mesure doivent être construits avec précaution et correctement étalonnés. Chaque mesure possède une incertitude associée, estimateur de la qualité de la mesure. Bien qu'une mesure soit donnée de manière usuelle par un nombre suivi d'une unité, elle possède donc en réalité trois composantes : l'estimation, l'incertitude et la probabilité que la mesure soit comprise dans un intervalle donné. Par exemple, la mesure de la longueur d'une planche peut donner 9 mètres plus ou moins 0,01 mètre, avec une probabilité de 0,95. Autrement dit, si l'on procède 100 fois à la mesure de cette longueur, environ 95 fois on trouvera une valeur comprise entre 8,99 mètre et 9,01 mètre (on parle d'intervalle de confiance à 95 %).

La mesure physique est fondamentale dans la plupart des champs scientifiques (chimie, physique, biologie, etc.). La mesure physique est aussi essentielle à un grand nombre d'applications industrielles et commerciales allant de l'ingénierie à la production manufacturière, en passant par la production pharmaceutique ou l'électronique.

Métrologie

En physique, la métrologie est considérée commel'étude de la mesure des grandeurs physiques, de la définition des leurs unités, et de la réalisation pratique des manipulations permettant d'arriver à un résultat numérique^[3].

En général, une métrique est un système de mesure, directe ou indirecte, définie par rapport à un étalon (ou standard) clairement défini et une échelle. La quantification d'une grandeur par le processus de mesure se base sur l'existence implicite ou explicite d'une métrique.

Mesure et dénombrement

La mesure se distingue habituellement du comptage ou dénombrement. Un compte est un nombre entier naturel et peut être exact. On peut par exemple dire qu'il y a douze œufs dans un carton en les dénombrant. Formellement, le dénombrement dépend de la logique. Il dépend de réponses à une question dont la réponse n'a que deux valeurs possibles, comme « Cet objet est-il un œuf ? ». En conséquence, une expression comme « ce carton contient 12 œufs » peut se décomposer en une combinaison de questions similaires, et peut être « vraie » ou « fausse ».

Il n'en va pas de même pour une mesure. Une mesure est le résultat d'une expérience ou manipulation d'un objet, permettant de calculer un nombre rationnel. On peut toujours trouver une petite différence de grandeur de l'objet pour laquelle deux expériences consécutives donnent le même résultat, et on peut toujours trouver une petite différence de résultat entre deux expériences consécutives.

Cependant, certains groupes ne peuvent être facilement dénombrés, et l'estimation de leur nombre se fait par inférence statistique à partir d'un échantillon dont la taille détermine une incertitude, comme pour une mesure physique.

Les méthodes de la mesure physique ne sont ainsi pas limitées aux grandeurs physiques. Des résultats et théories métrologiques peuvent être étendus à la quantification d'intensités de tous ordres, pourvu qu'on ait défini une métrique. Dans les sciences sociales, ainsi que dans d'autres champs de recherche comme la santé, la biologie et les études de marché, des modèles probabilistes comme le modèle de Rasch pour les mesures sont appliqués avec, pour instruments de mesure, des questionnaires et enquêtes et qui permettent les comparaisons entre personnes.

Les résultats de ces évaluations sont des nombres rationnels, qui sont souvent des proportions rapportées à une population totale, et non des comptages.

Choix des unités

Il est parfois plus judicieux de choisir une unité non-standard pour mesurer certaines grandeurs physiques. Ce choix peut dépendre notamment de l'ordre de grandeur (il est plus aisé de compter les distances interstellaires en années-lumière, par exemple) ou de l'utilisation que l'on veut en faire.

Toutefois, donner deux résultats de mesure de la même grandeur dans la même unité permet de comparer, et facilite l'interprétation des données, même si ça implique d'utiliser une unité qui ne correspond pas à sa dimension.

Difficultés de mesure et calcul de l'incertitude

Difficultés de mesure

Pour certaines quantités physiques, l'obtention de mesures précises peut être (très) difficile. L'exactitude absolue ne peut être atteinte : des mesures répétées vont varier en raison de différents facteurs comme la température, le temps, les champs électromagnétiques, et, évidemment, de la méthode de mesure. Il s'agit du concept de répétabilité. Ainsi la vitesse du son conserve tout de même une variance puisque sa valeur varie selon les conditions dans lesquelles la mesure est faite. Des techniques statistiques sont appliquées sur des échantillons de mesure afin d'estimer cette vitesse. Dans les campagnes plus anciennes de mesures, la variance était plus importante, et comparer les résultats indiquait que la variance et le biais n'étaient pas pris correctement en compte. Une preuve de ce fait a été fournie, lorsque pour des groupes de mesures variés, ont été tracés, avec la vitesse estimée, des barres d'erreurs indiquant la variance attendue pour la vitesse estimée. On a remarqué que les barres d'erreurs de chaque expérience ne se superposent pas toutes. Ceci indique que certains groupes ont considéré de manière incorrecte les sources d'erreurs potentielles et surestimé la précision de leurs méthodes.

Calcul d'incertitude

L'une des caractéristiques principales de la mesure physique est l'incertitude qu'elle possède intrinsèquement.

On peut améliorer la procédure de mesure et corriger les erreurs connues ou soupçonnées, le processus se termine toujours par une quantification, c'est-à-dire le choix d'une valeur prise dans un nombre fini de valeurs possibles. L'intervalle entre deux valeurs possibles est le minimum de l'incertitude ; souvent, on répète les mesures, et on obtient un jeu de résultats possédant une distribution statistique, expression élaborée de l'incertitude.

La définition de certaines grandeurs, comme la fréquence, implique une incertitude de mesure, puisqu'elle n'est définie par une intégrale de moins l'infini à plus l'infini, et donc à condition de connaître le phénomène périodique concerné sans aucune limite, ce qui n'est pas le cas dans une mesure.

Le processus de mesure comporte souvent des calculs qui peuvent faire intervenir plusieurs grandeurs, ou des fonctions de transfert qui ne sont pas nécessairement linéaires. On doit donc effectuer des calculs de propagation des incertitudes pour déterminer l'incertitude sur le résultat^[4].

Problème de la mesure en mécanique quantique

En mécanique quantique, c'est-à-dire à l'échelle atomique, deux phénomènes font obstacle à la mesure :

• le principe d'incertitude énoncé par Werner Heisenberg, concernant le couplage entre impulsion et position ;
• la fragilité de l'information quantique face aux mesures, qui fait que la mesure affecte l'objet mesuré.

Ces particularités font de la mesure à l'échelle particulaire un domaine en toute rigueur séparé de celui des mesures physiques à l'échelle macroscopique, qui concerne des objets dont la taille minimale est celle d'un point matériel, d'une particule matérielle ou d'une particule fluide.

Systèmes de mesures

Avant que les unités du système international soient adoptées dans le monde entier, il existait (de manière simultanée ou non) de nombreux systèmes, plus ou moins pratiques et plus ou moins généralisés en termes d'aires d'expansions, d'utilisations professionnelles ou autres.

Systèmes de mesures non métriques

Système impérial (GB, Commonwealth & US)

Les systèmes britanniques des unités anglaises, puis ultérieurement des unités impériales, étaient utilisées en Grande-Bretagne, dans le Commonwealth et aux États-Unis d'Amérique avant la généralisation du système international d'unités. Le système vint à être connu comme « unités d'échange U.S. » aux États-Unis d'Amérique où il est toujours appliqué, ainsi que dans certains pays des Caraïbes. Ces systèmes de mesures variés ont été un temps appelés pied-livre-seconde (PLS) d'après les noms des unités impériales pour la distance, la masse et le temps. La plupart des unités impériales sont toujours utilisées en Grande-Bretagne en dépit du basculement général vers le système international. Les panneaux routiers sont toujours en miles, yards, miles par heure, etc., les gens tendent à indiquer leurs mesures en pied et pouces, et la bière est vendue en pintes, pour donner quelques exemples. Les unités impériales sont utilisées dans de nombreux autres lieux ; en particulier dans de nombreux pays du Commonwealth qui sont pourtant considérés comme « métriques », les surfaces de terrains sont mesurées en acres et les surfaces de sol en pieds carrés, particulièrement dans les transactions commerciales (plus que dans les statistiques gouvernementales). De manière similaire, le gallon impérial est utilisé dans de nombreux pays considérés comme « métriques » dans les stations d'essences et pétrolières, comme dans les Émirats arabes unis.

Système métrique

Le système métrique est un système d'unités décimalisé basé sur le mètre et le gramme. Il existe dans de nombreuses variantes, avec différents choix d'unités de base, bien que cela n'affecte en rien ses applications quotidiennes. Depuis les années 1960, le système international d'unités (SI) - détaillé plus bas - est le système métrique standard internationalement reconnu. Les unités métriques de masse, de longueur, et d'électricité sont largement utilisées tant dans les applications quotidiennes que scientifiques. Le principal avantage du système métrique est qu'il possède une seule et unique unité de base pour chaque quantité physique. Toutes les autres unités sont des puissances de 10 de l'unité de base. Les conversions entre unités sont donc simples du fait qu'il suffit de multiplier (respectivement diviser) par 10, 100, 1000, etc. pour passer d'une unité à l'autre. Toutes les longueurs et distances sont, par exemple, mesurées en mètres, ou en millièmes de mètres (millimètres) ou en milliers de mètres (kilomètres) et ainsi de suite. Il n'y a donc pas profusion d'unités différentes avec des facteurs différents pour la conversion comme dans le système impérial. L'utilisation de fraction (par exemple 2/5 de mètre) n’est pas interdit mais est peu usuel.

Système international

Généralités

Le système international d'unités (abrégé en SI) est la forme moderne et révisée du système métrique. C'est le système d'unités le plus répandu dans le monde, à la fois dans la vie courante et dans les domaines scientifiques. Le SI a été développé dans les années 1960 à partir du système MKS (mètre-kilogramme-seconde) préférentiellement au système CGS (centimètre-gramme-seconde), qui possède de multiples variantes. Le SI introduit dès ses débuts de nombreuses et nouvelles unités ne faisant pas partie initialement du système métrique.

Il y a deux types d'unités SI, les unités de base et les unités secondaires. Les unités de base sont les mesures correspondant au temps, à la longueur, à la masse, à la température, à la quantité (d'objets), au courant électrique, et l'intensité lumineuse. Les unités secondaires sont construites sur les unités de base ; par exemple la masse volumique qui s'exprime en kg/m³.

Préfixes de conversion

Pour « éliminer » les préfixes, l'utilisation de la multiplication est le plus simple. Convertir les mètres en centimètres revient à multiplier les quantités en mètres par 100, puisqu'il y a 100 centimètres dans un mètre. Et inversement.

Les grandeurs de base

Longueur

Les longueurs mesurées s'expriment dans le système international en mètre (symbole : m). Dans la vie courante, et selon les cas, on fait régulièrement usage des multiples courants que sont le kilomètre, le centimètre et le millimètre :

• les mesures de superficies sont « homogènes » à des longueurs au carré (L²), ce que l'on retrouve facilement dans l'expression des unités secondaires : kilomètre carré, mètre carré, etc. mais pas pour are (100 m²) ou hectare (10 000 m²).
• les mesures de volume sont « homogènes » à des longueurs au cube (L³). L'unité de base « dérivée » est donc le mètre cube. Cependant, on utilise de manière usuelle le litre qui est égal à un décimètre cube.

Temps

Les mesures du temps s'effectuent dans le système international en seconde. La seconde est la seule unité du système international dont l'usage conserve une référence au système de comptage sexagésimal, possédant des unités dérivées d'ordre supérieur qui ne sont pas multiples de 10 de l'unité de base, mais multiples de 60 (minute, heure), puis de 24 (jour), etc.

Masse

La masse est habituellement exprimée en kilogramme (usuellement appelé "kilo", symbole : kg). Cette appellation rappelle que le kilogramme est à l'origine un multiple du gramme, unité de base du système CGS. On pourra noter que ceci a conduit à conserver un nom spécifique pour le multiple de mille kilogrammes qui n'est jamais appelé kilokilogramme mais est connu sous le nom de tonne (symbole : T).

Température

L'unité de température absolue du système international est le kelvin (K), mesure directe de l'agitation thermique. Cette unité est utilisée de manière usuelle dans le domaine scientifique. Dans la vie courante (hors espace américain anglophone), l'unité utilisée est le degré dit "Celsius" (°C) (anciennement appelé centigrade) - dont l'échelle fut construite sur les phénomènes de fusion-ébullition de l'eau, qui se déduit de l'échelle Kelvin par la transformation suivante : température (°C) + 273,15 = température (K).

Quantité de matière

Une quantité de matière (Q) est exprimée selon l'échelle molaire dont l'unité est la mole (mol). Cette unité correspond à 6,02.10²³ objets (nombre d'Avogadro). Elle est fréquemment utilisée en chimie, particulièrement pour les mesures de densité ("homogène" à Q/L³) qui rapportent la quantité de matière (ou d'objets chimiques) à un volume.

Courant électrique

L'intensité du courant électrique est mesurée en ampère (A) dans le système international, à partir duquel sont dérivées les autres unités appliquées pour les mesures de courant électrique (c'est-à-dire le volt (V) pour la différence de potentiel et l'ohm (Ω) pour la résistance, entre autres).

Intensité lumineuse

Dans le système international, l'intensité lumineuse (sous-entendu perçue par l'œil humain) est mesurée par une échelle dont l'unité de base est la candela (cd, à ne pas confondre avec "Cd", symbole chimique du cadmium).

Grandeurs et unités secondaires

Grandeurs secondaires à dimensions non nulles et unités utilisées

Dans le tableau ci-après sont présentées des grandeurs secondaires à dimensions non nulles et leurs unités^[5], ainsi que quelques instruments de mesures.

Dimension	Unité secondaire	Symbole (S.I.)	Homogène à	Exemples d'unités dérivées	Instruments de mesures
Accélération	mètre par seconde au carré	m.s-2	L.T-2		Accéléromètre
Masse volumique	kilogramme par mètre cube	ρ	M.L-3		Pycnomètre
Énergie	joule	J	M.L2.T-2	calorie	Calorimètre
Force	newton	N	M.L.T-2		Dynamomètre
Fréquence	hertz	Hz	T-1		Fréquencemètre
Pression	pascal	Pa	M.L-1.T-2	bar, torr	Manomètre
Puissance	watt	W	M.L2.T-3		Wattmètre
Superficie	mètre carré	m2	L2	are, hectare
Vitesse	mètre par seconde	m.s-1	L.T -1	kilomètre par heure	Vélocimètre
Volume	mètre cube	m3	L3	litre

Grandeurs à dimension nulle et unités utilisées

Les grandeurs se présentant comme un rapport de grandeurs de mêmes dimensions sont adimensionnelles au sens mathématique du terme (leur dimension est nulle) et sont donc des scalaires. Leur unité est donc (généralement) le nombre 1 et ne porte pas de nom, bien que certaines grandeurs peuvent s'exprimer dans des unités portant des noms spécifiques^[5] (elles restent cependant adimensionnelles). Parmi ces dernières, on peut trouver la mesure d'angle plan ou solide (respectivement radian et stéradian), la mesure de rapport entre deux puissances (en décibel ou bel), entre autres.

Les échelles dans lesquelles ces mesures peuvent également être exprimées dans un système non décimal (comme le système sexagésimal pour une mesure d'angle exprimée en degrés, qui est calquée sur la mesure du temps) ou dans une échelle non linéaire (par exemple logarithmique pour la mesure du rapport entre deux puissances).

Moyens de mesure

Grandeurs étalons

Longueur

Une « règle » est un outil utilisé en géométrie, dessin technique, et autres afin de mesurer les distances et/ou tracer des lignes droites. Strictement parlant, un té est l'instrument utilisé pour tracer les lignes et l'instrument calibré pour la détermination des mesures est appelé "règle". De nombreuses et différentes formes d'instruments flexibles sont utilisées pour déterminer les longueurs, comme le mètre de charpentier, le mètre-ruban utilisé par les tailleurs, le mètre rétractable utilisé par les hommes de chantier, pied à coulisse, etc.

Dans des contextes particuliers, on utilise d'autres instruments de mesure de longueur. À l'échelle microscopique, la profilométrie laser permet de mesurer un profil avec une précision de quelques dizaines de nanomètres. À l'échelle « humaine », on peut employer des télémètres.

Temps

Les outils de mesure les plus communs pour la mesure du temps sont les horloges, pour des périodes inférieures au jour, et le calendrier pour des périodes supérieures. Les horloges se déclinent en genres plus ou moins exotiques allant des montres à l'Horloge de Long Now. Elles peuvent être pilotées par de nombreux mécanismes, comme le pendule par exemple. Il y a également une grande variété de calendriers, par exemple le calendrier lunaire et le calendrier solaire, bien que le plus utilisé soit le calendrier grégorien.

Le chronomètre (maritime) est un outil de mesure du temps assez précis pour être utilisé comme standard de temps portable, habituellement utilisé pour la détermination des longitudes par le biais de la navigation astronomique.

Le type le plus précis d'instruments de mesure du temps est l'horloge atomique. Elle est à comparer avec des instruments plus anciens et plus rudimentaires, comme le sablier, le cadran solaire ou la clepsydre.

Masse

Une échelle de masse (et non de poids) est une référence pour la mesure de masse d'un corps. En dehors des outils numériques, le meilleur moyen de mesurer la masse est l'utilisation d'une balance. Dans sa forme conventionnelle, cette classe d'instruments de mesure compare l'échantillon, placé dans un plateau (de mesure) et suspendu à une extrémité d'un fléau, l'autre soutenant un plateau (de référence) suspendu dans lequel est placé une masse-étalon (ou une combinaison de masses-étalon). Afin de procéder à la mesure de la masse de l'objet placé dans le plateau, des masses (appelées couramment mais de manière inappropriée "poids") sont ajoutées dans le plateau de référence jusqu'à ce que le fléau soit autant en équilibre (mécanique) que possible. Une manière moins précise de procéder à une mesure de masse basée sur la déformation d'un ressort calibré qui se déforme linéairement en fonction de la masse supportée.

La notion de masse peut aussi se référer à l'inertie d'un objet.

Température

La température est une grandeur physique mesurée à l’aide d’un thermomètre et étudiée en thermométrie. Dans la vie courante, elle est reliée aux sensations de froid et de chaud, provenant du transfert thermique entre le corps humain et son environnement. En physique, elle se définit de plusieurs manières : comme fonction croissante du degré d’agitation thermique des particules (en théorie cinétique des gaz), par l’équilibre des transferts thermiques entre plusieurs systèmes ou à partir de l’entropie (en thermodynamique et en physique statistique). La température est une variable importante dans d’autres disciplines : météorologie et climatologie, médecine, et chimie. L’échelle de température la plus répandue est le degré Celsius, dans laquelle la glace (formée d'eau) fond à 0 °C et l'eau bout à environ 100 °C dans les conditions standard de pression. Dans les pays utilisant le système impérial (anglo-saxon) d’unités, on emploie le degré Fahrenheit où la glace fond à 32 °F et l'eau bout à 212 °F. L’unité du système international d'unités (SI), d’utilisation scientifique et définie à partir du zéro absolu, est le Kelvin dont la graduation est presque identique à celle des degrés centigrades.

À partir de :	Kelvin	Celsius	Fahrenheit	Rankine	Réaumur

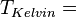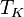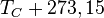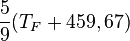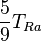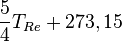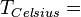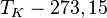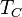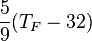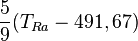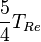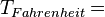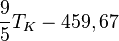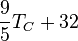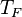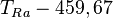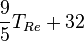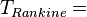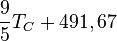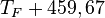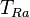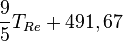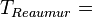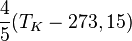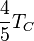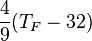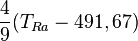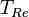Intensité électrique

Un courant électrique est un déplacement d'ensemble de porteurs de charges électriques, généralement des électrons, au sein d'un matériau conducteur. Ces déplacements sont imposés par l'action de la force électromagnétique, dont l'interaction avec la matière est le fondement de l'électricité. L'intensité du courant électrique (parfois désignée « ampérage »3,4,5,6) est un nombre décrivant le débit de charge électrique à travers une surface donnée, notamment la section d'un fil électrique :

.

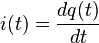où :
i est l'intensité du courant ;
q la charge électrique ;
t le temps.
Dans le système international d'unités, l'intensité du courant se mesure en ampères, une unité de base dont le symbole normalisé est A. Un ampère correspond à un débit de charge d'un coulomb par seconde. L'intensité se mesure à l'aide d'un ampèremètre qui doit être branché en série dans le circuit.

Radiométrie et Photométrie

Valeur photométrique	Symbole	Unité SI (symbole)	Valeur radiométrique	Symbole	Unité SI (symbole)	Dimension
Quantité de lumière		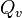lumen seconde (lm⋅s)	Énergie rayonnante		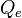joule (J)	M⋅L2⋅T−2
Flux lumineux		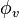lumens ou watts	Flux rayonnant		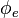watt (W)	M⋅L2⋅T−3
Intensité lumineuse		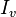candelas	Intensité rayonnante		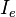watt par stéradian (W⋅sr−1)	M⋅L2⋅T−3
Luminance		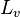candelas par mètre carré (candela.m−2)	Rayonnance/Radiance		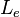watt par stéradian par mètre carré (W⋅sr−1⋅m−2)	M⋅T−3
Eclairement lumineux		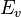lux	Éclairement énergétique		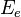watt par mètre carré (W⋅m-2)	M⋅T−3
Émittance lumineux [6]		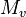lux	Émittance		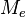watt par mètre carré (W⋅m-2)	M⋅T−3
Exposition lumineuse		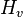lx⋅s	Exposition		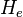joule par mètre carré (J⋅m-2)	M⋅T−2

Grandeurs dérivées

Force

Une force (dont l'intensité est exprimée couramment en newtons qui a la dimension masse*longueur/(temps²)) peut se mesurer avec différents instruments dont le plus simple est le dynamomètre, qui consiste en un ressort assorti de graduations. Certains des instruments de mesure de masse, ceux qui n'utilisent pas de masse de référence, mesurent en réalité une force, et convertissent en utilisant la valeur du champ de gravité terrestre. Ainsi, une balance à plateau serait aussi exacte sur la Lune que sur la Terre, tandis qu'une balance à ressort ou électronique se tromperait d'un facteur six.

Pression

La pression se mesure à l'aide d'un baromètre dans le cadre météorologique (variations modérées autour de un bar) ou d'un manomètre pour les variations plus grandes. La pression correspond à une force par unité de surface. Il existe plusieurs types d'instruments :

• Le baromètre de Torricelli consiste en une colonne renversée remplie de mercure, dont le sommet est à pression quasi nulle. On mesure alors la hauteur de liquide qui compense la pression atmosphérique (voir : poussée d'Archimède).
• Le baromètre à gaz utilise la variation de volume d'un gaz. Celle-ci dépend autant que de la température que de la pression, il faut donc utiliser en même temps un thermomètre pour effectuer une compensation.
• Le baromètre anéroïde utilise la déformation d'une capsule sous vide, principe repris en microtechnologie par les microsystèmes capacitifs de mesure de pression.

Voir aussi

Bibliographie

• Jean Hladik, Unités de mesure : étalons et symboles des grandeurs physiques, Paris, Masson, coll. « Mesures physiques »,‎ 1992
• Albert Pérard, Les mesures physiques, Paris, PUF, coll. « Que sais-je ? » (n^o 244),‎ 1968, 4^e éd. (1^re éd. 1947)
• Gérard Prieur (coord.), Mustapha Nadi (dir.), Long-Den Nguyen (dir.) et Gérard Tsalkovitch (dir.), La mesure et l'instrumentation : état de l'art et perspectives, Paris, Masson, coll. « Mesures physiques »,‎ 1995 préface de Georges Charpak.

Articles connexes

• Métrologie
• Conférence générale des poids et mesures

Liens externes

• Bureau International des Poids et Mesures
• (en) The NIST Guide for the use of the International System of Units
• Le Système international d'unités, 8^e édition, 2006, Bureau international des poids et mesures [PDF]

Notes et références

• Portail de la physique
• Portail de la chimie