Particule matérielle
La matière est pleine de vide. Un corps de matière solide ou fluide est un domaine discontinu de particules élémentaires (protons, neutrons, électrons, etc.). Les dimensions des particules élémentaires sont très petites devant les distances qui les séparent.
Une grandeur physique (pression, masse volumique, vitesse, etc.), liée à des phénomènes physiques se produisant dans un espace situé à l'intérieur d'un corps, ne peut être définie en un point situé dans cet espace que si celui-ci contient un nombre suffisamment grand de particules élémentaires : figure 1.3, une grandeur physique caractérise, en un point  , les particules élémentaires situées dans un espace
, les particules élémentaires situées dans un espace  contenant le point
contenant le point  .
.
Le terme particule matérielle[1] (material particle[2] en anglais) désigne une petite portion d'un corps, de matière solide ou fluide, constituée de ce nombre suffisamment grand de particules élémentaires : figure 1.3, l'espace 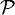 est occupé par une particule matérielle contenant le point
est occupé par une particule matérielle contenant le point  .
.
Donnons des synonymes de « particule matérielle » : petit élément[3], élément de volume macroscopique [4], élément de volume représentatif [5], particule macroscopique[6], et volume élémentaire représentatif[7].
Une particule matérielle contenant de la matière fluide pourra être qualifiée de particule fluide[8],[9],[10] ou de parcelle fluide[11].
Une grandeur physique doit donc caractériser une particule matérielle pour être une fonction continue des coordonnées du point, en un point situé à l'intérieur de cette particule.
- Fig.1 : Corps, particules élémentaires et particules matérielles
-

1. Corps solides et corps fluides
-

2. Corps quelconque
-

3. Particules élémentaires dans une particule matérielle.
-
4. Particules matérielles contenant un même point.
Les valeurs d'une grandeur physique, caractérisant des particules matérielles contenant un même point d'un corps, sont toutes identiques: figure 1.4, les particules matérielles 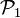 et
et  contiennent un même point
contiennent un même point  .
Cela signifie que ce point ne doit pas être situé sur une surface de discontinuité.
Comme nous le verrons la masse volumique ne peut pas être définie en des points situés sur une telle surface.
.
Cela signifie que ce point ne doit pas être situé sur une surface de discontinuité.
Comme nous le verrons la masse volumique ne peut pas être définie en des points situés sur une telle surface.
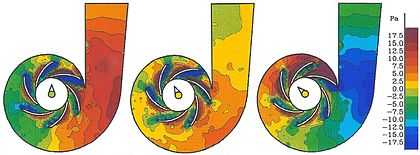
D'une manière générale, les phénomènes physiques doivent être caractérisés grâce à des grandeurs physiques dont les valeurs varient, d'un point à l'autre, à l'intérieur d'un corps et d'un instant à l'autre, en tous les points du corps (figure 2). Dans ce cas, le nombre suffisamment grand de particules élémentaires contenu par une particule matérielle ne doit pas être trop grand. Les grandeurs physiques, relatives à une particule matérielle, doivent dépendre le moins possible de la position que la particule occupe par rapport à un point qu'elle contient. Ainsi les grandeurs physiques seront définies, en chaque point d'un corps, avec le maximum de précision. C'est pourquoi, la particule matérielle devra être suffisamment petite à l'échelle du corps qui la contient.
Une grandeur physique doit être liée à des phénomènes physiques qui se produisent dans une particule matérielle afin que cette grandeur physique puisse être définie en un point contenu par cette particule. Dans ces conditions, une grandeur physique moyenne peut être assimilée à une grandeur physique ponctuelle à l'échelle d'un corps.
Ainsi un champ d'une grandeur physique dans un corps peut être reconstitué (figure 2). En un point d'un corps, à une valeur d'une grandeur physique ponctuelle, à l'échelle de ce corps, correspond donc une valeur d'une grandeur physique moyenne relative à une particule matérielle contenant ce point.
En outre une grandeur physique moyenne (grandeur physique mesurée, grandeur thermodynamique) peut être comparée à une grandeur physique ponctuelle solution des équations physiques des milieux continus.
Les relations liant, entre elles, les grandeurs thermodynamiques, pourront contribuer à la résolution de ces équations.
Mathématiques, Thermodynamique et Mesure
Les phénomènes physiques, se produisant à l'intérieur d'un corps de matière solide ou fluide, peuvent être produits mathématiquement à l'intérieur d'un domaine continu de points auquel le corps peut être assimilé. Ce domaine occupe la totalité de l'espace limité par la frontière extérieure du corps.
Une grandeur physique relative à une particule matérielle est une grandeur physique moyenne que l'on peut attribuer à un point que la particule contient. Cette grandeur est, en ce point, une grandeur physique ponctuelle à l'échelle du corps. Elle peut être une grandeur mesurée et/ou une grandeur thermodynamique. À cette grandeur physique ponctuelle, à l'échelle du corps, correspond une grandeur physique ponctuelle d'un point de vue mathématique. Cette dernière grandeur caractérise les phénomènes physiques produits mathématiquement en un point que la particule contient. En chacun des points d'un domaine continu de points géométriques, les valeurs, prises par cette vraie grandeur physique ponctuelle, sont des solutions d'équations mathématiques représentant un modèle mathématique du corps de matière solide ou fluide. Une grandeur physique ponctuelle est, en un point d'un domaine, relative à une portion infiniment petite qui, située à l'intérieur de ce domaine, contient ce point (parcelle infinitésimale). Nous pouvons considérer qu'il s'agit aussi d'une grandeur attribuée à chaque point d'un domaine continu de points géométriques.
Une grandeur physique ponctuelle  doit donc être définie en chaque point
doit donc être définie en chaque point  d'un domaine et à chaque instant
d'un domaine et à chaque instant 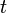 .
C' est donc une fonction continue des coordonnées
.
C' est donc une fonction continue des coordonnées 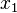 ,
, 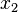 et
et 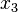 du point
du point  et du temps
et du temps 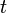 :
:
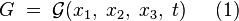 .
.
Cela signifie que, les valeurs de la fonction 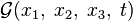 , relatives à toutes les parcelles infinitésimales pouvant contenir un même point géométrique
, relatives à toutes les parcelles infinitésimales pouvant contenir un même point géométrique  , sont, à chaque instant, toutes identiques (figure 1.4).
, sont, à chaque instant, toutes identiques (figure 1.4).
Masse volumique physique
La masse volumique est une grandeur physique mesurable (masse volumique physique).
Elle est facilement perceptible par les organes des sens et par l'esprit : un décimètre cube d'eau est un étalon de masse volumique représentant matériellement un kilogramme par décimètre cube 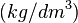 (voir Masse volumique).
Qu'elle soit celle d'un corps de matière solide ou fluide ou d'une parcelle de ce corps, la masse volumique physique a la même signification physique.
(voir Masse volumique).
Qu'elle soit celle d'un corps de matière solide ou fluide ou d'une parcelle de ce corps, la masse volumique physique a la même signification physique.
La masse volumique  d'une parcelle
d'une parcelle 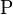 d'un corps de matière solide ou fluide est égale au quotient de la masse
d'un corps de matière solide ou fluide est égale au quotient de la masse 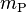 de cette parcelle sur le volume
de cette parcelle sur le volume 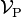 qu'elle occupe :
qu'elle occupe :
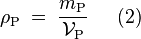 .
.
La matière est pleine de vide. En dessous d'une certaine dimension, la plupart des parcelles d'un corps solide ou fluide ne contiennent plus de particules élémentaires (protons, neutrons, négatons, etc.). Un corps de matière solide ou fluide est un domaine discontinu de particules élémentaires. C'est pourquoi, comme nous le verrons, la masse volumique de n'importe quelle parcelle d'un corps ne pourra pas être, à la fois, une fonction continue en tout point d'un corps et une grandeur physique ponctuelle, d'un point de vue mathématique. En effet, la masse volumique d'une parcelle d'un corps ne sera une fonction continue en tout point d'un corps que si cette parcelle contient un nombre suffisamment grand de particules élémentaires. Cette parcelle devra être, tout de même, suffisamment petite afin que sa masse volumique soit, à l'échelle du corps, suffisamment ponctuelle : c'est la description d'une particule matérielle. La masse volumique d'une particule matérielle n'est donc pas une grandeur ponctuelle d'un point de vue mathématique : elle l'est seulement à l'échelle d'un corps. Les masses volumiques de toutes les particules matérielles, contenant un même point, ont toutes la même valeur, sauf en des points qui seraient situés sur des surfaces de discontinuité.
Caractérisons, maintenant, une particule matérielle.
Exemple simple de domaine discontinu
Imaginons un corps 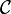 ayant la forme d'un parallélépipédique rectangle (figure 3.1) qui, afin de simplifier les calculs, est constitué d' éléments de masse de formes cubiques (figure 3.2).
Ces éléments de masse sont tous identiques.
Ils sont immobiles par rapport au corps
ayant la forme d'un parallélépipédique rectangle (figure 3.1) qui, afin de simplifier les calculs, est constitué d' éléments de masse de formes cubiques (figure 3.2).
Ces éléments de masse sont tous identiques.
Ils sont immobiles par rapport au corps  et régulièrement espacés entre eux (figure 3.3).
et régulièrement espacés entre eux (figure 3.3).
- Fig.3 : Ensemble discontinu d'éléments de masse (corps C)
-

1. Corps C
-

2. Intérieur du corps C
-
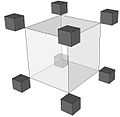
3. Espace entre des éléments
Un élément de masse quelconque est désigné par 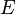 .
La masse d'un élément de masse et la masse volumique de celui-ci sont respectivement désignées par
.
La masse d'un élément de masse et la masse volumique de celui-ci sont respectivement désignées par 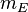 et par
et par  .
Selon la dimension d'une parcelle du corps
.
Selon la dimension d'une parcelle du corps 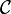 , nous pouvons envisager plusieurs cas.
, nous pouvons envisager plusieurs cas.
- Cas 1 : Considérons une parcelle
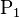 dont le volume
dont le volume 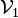 est plus petit que celui d'un élément de masse (figure 4.1).
est plus petit que celui d'un élément de masse (figure 4.1).
La parcelle 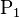 contient un point
contient un point  situé sur la frontière d'un élément de masse
situé sur la frontière d'un élément de masse 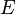 .
Par rapport à l' élément de masse, déplaçons la parcelle
.
Par rapport à l' élément de masse, déplaçons la parcelle 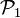 , perpendiculairement à l'une des faces de cet élément, tout en conservant le point
, perpendiculairement à l'une des faces de cet élément, tout en conservant le point  dans la parcelle
dans la parcelle  (figures 4.2).
(figures 4.2).
- Fig.4 : Positions de parcelles sur l'axe X
-

1. Parcelle centrée en

-

2. Parcelle centrée en
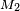
-
3. Parcelle centrée en
-
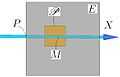
4. Parcelle centrée en
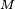
La masse 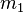 de la parcelle
de la parcelle 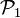 dépend de la position qu'elle occupe de part et d'autre de cette frontière.
Le volume
dépend de la position qu'elle occupe de part et d'autre de cette frontière.
Le volume 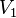 de la parcelle
de la parcelle 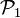 ne change pas.
La masse volumique
ne change pas.
La masse volumique 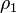 de la parcelle
de la parcelle 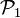 dépend donc de cette position (figure 5).
dépend donc de cette position (figure 5).
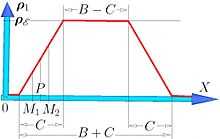
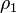 de la parcelle P1 selon sa position sur X
de la parcelle P1 selon sa position sur XLe graphe montrant l'évolution de la masse volumique de la parcelle 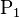 , en fonction de la position de cette parcelle, est un graphe continu (figure 5).
La masse volumique de la parcelle
, en fonction de la position de cette parcelle, est un graphe continu (figure 5).
La masse volumique de la parcelle 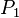 n'est pas pour autant une fonction continue: la valeur de cette fonction ne peut pas être définie au point P.
En effet, la masse volumique de la parcelle
n'est pas pour autant une fonction continue: la valeur de cette fonction ne peut pas être définie au point P.
En effet, la masse volumique de la parcelle 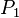 contenant le point P dépend de la position que celle-ci occupe.
La masse volumique au point
contenant le point P dépend de la position que celle-ci occupe.
La masse volumique au point  ne pourra pas être déterminée à partir de la masse volumique d'une parcelle
ne pourra pas être déterminée à partir de la masse volumique d'une parcelle 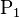 contenant le point
contenant le point  .
Si une parcelle
.
Si une parcelle 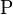 contient un point
contient un point 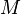 et que, dans aucune de ses positions, elle ne puisse contenir un point
et que, dans aucune de ses positions, elle ne puisse contenir un point  situé sur la frontière d'un élément de masse alors la masse volumique pourra être définie en ce point
situé sur la frontière d'un élément de masse alors la masse volumique pourra être définie en ce point 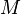 : elle sera égale à zéro si le point
: elle sera égale à zéro si le point 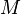 est situé à l'extérieur de cet élément (figure 4.3) et égale à
est situé à l'extérieur de cet élément (figure 4.3) et égale à  si le point
si le point 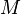 est situé dans un élément de masse (figure 4.4).
est situé dans un élément de masse (figure 4.4).
La masse volumique d'une parcelle 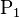 n'est pas une fonction continue en tous les points situés à la surface d'un élément de masse.
La masse volumique d'une parcelle
n'est pas une fonction continue en tous les points situés à la surface d'un élément de masse.
La masse volumique d'une parcelle 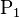 n'est pas une fonction continue en de trop nombreux points du corps
n'est pas une fonction continue en de trop nombreux points du corps 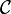 : elle ne pourra donc pas avoir un usage théorique en Mécanique des fluides et en Résistance des matériaux.
: elle ne pourra donc pas avoir un usage théorique en Mécanique des fluides et en Résistance des matériaux.
- Cas 2 : Considérons, maintenant, une parcelle
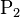 de volume
de volume 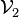 .
.
Elle contient  éléments de masse du corps
éléments de masse du corps 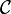 (
(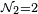 sur la figure 6.1).
Désignons par
sur la figure 6.1).
Désignons par  un point géométrique que la parcelle
un point géométrique que la parcelle 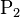 contient.
Puisque la masse de
contient.
Puisque la masse de 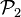 est à égale à
est à égale à  , la masse volumique de
, la masse volumique de 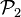 est égale à :
est égale à :
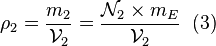 .
.
Considérons une autre parcelle, une parcelle 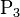 , contenant la parcelle
, contenant la parcelle 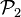 : son volume
: son volume  est donc plus grand que le volume
est donc plus grand que le volume 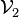 de la parcelle
de la parcelle 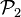 (figure 6.2).
La parcelle
(figure 6.2).
La parcelle 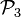 contient donc aussi le point
contient donc aussi le point  .
.
- Fig.6 : Masse volumique en un point
-

1. Parcelle P2
-
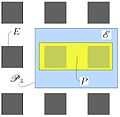
2. Parcelle P3
-
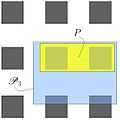
3. Délacement de P3
A priori, du fait de l'espacement des éléments de masse, les valeurs des masses volumiques 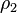 et
et 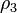 ne peuvent pas être égales.
ne peuvent pas être égales.

 d'une parcelle de matière selon son volume
d'une parcelle de matière selon son volume 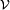 :
: 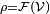
Afin d'examiner cela, appelons 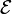 la portion de l'espace que la particule
la portion de l'espace que la particule 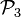 occupe mais que n'occupe pas la particule
occupe mais que n'occupe pas la particule 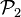 :
:
- 1. Si la portion
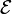 est vide.
est vide.
- 1. Si la portion
Les deux parcelles 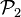 et
et 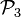 contiennent les mêmes éléments de masse.
Les masses
contiennent les mêmes éléments de masse.
Les masses 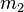 et
et 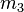 de ces deux parcelles sont égales.
Puisque le volume
de ces deux parcelles sont égales.
Puisque le volume 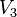 est plus grand que le volume
est plus grand que le volume 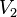 , la masse volumique
, la masse volumique 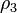 sera donc plus petite que la masse volumique
sera donc plus petite que la masse volumique 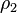 :
:
 .
.
- 2. Si la portion
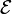 contient un ou plusieurs éléments de masse.
contient un ou plusieurs éléments de masse.
- 2. Si la portion
Les valeurs des masses volumiques 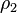 et
et 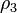 sont aussi, dans ce cas, différentes l'une de l'autre.
La masse volumique d'une parcelle, contenant un point du corps
sont aussi, dans ce cas, différentes l'une de l'autre.
La masse volumique d'une parcelle, contenant un point du corps 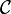 , dépend du volume que la parcelle occupe.
C'est ce que montre le graphe de la figure 7.
Celui a été obtenu par calcul[12].
, dépend du volume que la parcelle occupe.
C'est ce que montre le graphe de la figure 7.
Celui a été obtenu par calcul[12].
Toutefois, la masse volumique 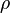 d'une parcelle ne varie quasiment plus en fonction de son volume lorsque ce dernier dépasse une certaine valeur.
Cette condition peut être traduite par: lorsqu'une parcelle contient un nombre suffisant d' éléments de masse.
Nous pourrions interpréter ces premières observations afin de conclure que la masse volumique d'une parcelle d'un corps, ayant un volume suffisant grand, est une fonction continue.
Mais poursuivons ; la conclusion n'en sera que plus facile.
d'une parcelle ne varie quasiment plus en fonction de son volume lorsque ce dernier dépasse une certaine valeur.
Cette condition peut être traduite par: lorsqu'une parcelle contient un nombre suffisant d' éléments de masse.
Nous pourrions interpréter ces premières observations afin de conclure que la masse volumique d'une parcelle d'un corps, ayant un volume suffisant grand, est une fonction continue.
Mais poursuivons ; la conclusion n'en sera que plus facile.
- Cas 3 : Supposons maintenant que, par rapport aux éléments de masse, qui sont, rappelons le, immobiles par rapport au corps, nous déplacions la frontière de la parcelle
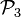 sans que ne soit changé le volume de cette parcelle (figure 6.3).
sans que ne soit changé le volume de cette parcelle (figure 6.3).
Dans l'exemple de la figure 6.3, la masse 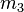 augmente ; donc la masse volumique
augmente ; donc la masse volumique 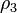 augmente aussi.
D'une manière générale, des résultats de calculs[12] montrent que la masse volumique d'une parcelle du corps
augmente aussi.
D'une manière générale, des résultats de calculs[12] montrent que la masse volumique d'une parcelle du corps 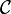 variera, aussi, en fonction de la position qu'elle occupe à l'intérieur de ce corps (figure 8).
variera, aussi, en fonction de la position qu'elle occupe à l'intérieur de ce corps (figure 8).

 d'une parcelle selon sa position
d'une parcelle selon sa position  et son volume
et son volume 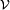 :
: 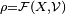
Les éléments de masse constituant le corps  sont tous identiques et uniformément répartis.
Pourtant, les masses volumiques de toutes les petites parcelles du corps C peuvent avoir des valeurs très différentes; même les masses volumiques des parcelles qui, très proches l'une de l'autre, occupent partiellement un même espace.
Ainsi, toutes les petites parcelles contenant un même point n'auront pas la même masse volumique.
Dans ce cas, nous ne pourrons pas définir une valeur unique de la masse volumique en un point précis du corps
sont tous identiques et uniformément répartis.
Pourtant, les masses volumiques de toutes les petites parcelles du corps C peuvent avoir des valeurs très différentes; même les masses volumiques des parcelles qui, très proches l'une de l'autre, occupent partiellement un même espace.
Ainsi, toutes les petites parcelles contenant un même point n'auront pas la même masse volumique.
Dans ce cas, nous ne pourrons pas définir une valeur unique de la masse volumique en un point précis du corps  .
Cependant, nous pouvons constater qu'une parcelle dont la masse volumique ne varie plus quasiment plus en fonction de son volume et, aussi, une parcelle dont la masse volumique ne varie quasiment plus lorsque sa position change : la masse volumique de ces parcelles peut donc être considérée comme une fonction continue en tout point situé à l'intérieur du corps
.
Cependant, nous pouvons constater qu'une parcelle dont la masse volumique ne varie plus quasiment plus en fonction de son volume et, aussi, une parcelle dont la masse volumique ne varie quasiment plus lorsque sa position change : la masse volumique de ces parcelles peut donc être considérée comme une fonction continue en tout point situé à l'intérieur du corps  .
.
Corps solide ou fluide
Un corps de matière solide ou fluide est un domaine discontinu de particules élémentaires.
Les particules élémentaires sont des éléments de masse répartis dans un espace.
La masse volumique d'une parcelle d'un corps de matière solide ou fluide présente donc des caractéristiques semblables à celle de la masse volumique d'une parcelle du corps  .
Une parcelle de matière solide ou fluide doit aussi avoir un volume au-delà duquel la masse volumique de cette parcelle ne varie plus en fonction du volume et de la position de celle-ci.
Désignons par
.
Une parcelle de matière solide ou fluide doit aussi avoir un volume au-delà duquel la masse volumique de cette parcelle ne varie plus en fonction du volume et de la position de celle-ci.
Désignons par 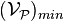 , le volume minimum qu'une parcelle doit avoir pour que sa masse volumique soit une fonction continue dans l'espace : les particules élémentaires, contenues dans cette parcelle, constitue une parcelle matérielle.
, le volume minimum qu'une parcelle doit avoir pour que sa masse volumique soit une fonction continue dans l'espace : les particules élémentaires, contenues dans cette parcelle, constitue une parcelle matérielle.
La répartition des particules élémentaires peut varier d'un point à l'autre d'un corps (fluide compressible) ; c'est-à-dire que l'espacement des particules élémentaires n'est pas le même en tout point du corps.
Cette variation de la répartition des particules élémentaires dans un corps, perceptible à l'échelle de ce corps, doit être révélée.
Dans ce cas, la masse volumique d'une parcelle matérielles doit dépendre de la position d'un point quelconque que la parcelle matérielle contient et, en plus, les masses volumiques de toutes les particules de matière, pouvant contenir ce point quelconque, doivent avoir des valeurs égales entre elles ; sauf en des points qui seraient situés sur une surface de discontinuité.
La masse volumique d'une parcelle matérielle est une grandeur moyenne qui doit être, en chaque point du corps, une fonction continue, mais aussi, une fonction suffisamment ponctuelle à l'échelle du corps.
C'est pourquoi, le volume d'une parcelle de matière doit rester suffisamment petit à l'échelle du corps afin que la masse volumique de la parcelle puisse rendre compte de la présence d'une quantité matière à l'intérieur de petits espaces par rapport à celui occupé par le corps.
En effet, plus le volume d'une parcelle de matière augmente et plus les variations d'une grandeur physique, à l'intérieur d'un corps, vont être atténuées.
Le volume d'une parcelle doit être inférieur à un volume maximum : un volume au-delà duquel la masse volumique ne fournit plus une assez grande précision de la masse volumique à l'intérieur du corps.
Nous désignerons, ce volume maximum, par 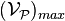 .
.
D'une manière générale, à l'intérieur d'un espace occupé par un corps (fluide compressible), la loi des gaz parfaits doit donc être prise en compte par le modèle mathématique.
En thermodynamique classique, la masse volumique n'est pas une grandeur ponctuelle : elle est relative à une quantité minimum de matière (particule thermodynamique).
Désignons par 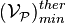 le volume minimum que doit avoir la particule thermodynamique afin que les lois de la thermodynamique puissent être appliquées à la matière que la parcelle contient.
le volume minimum que doit avoir la particule thermodynamique afin que les lois de la thermodynamique puissent être appliquées à la matière que la parcelle contient.
Surface de discontinuité
Sur la figure 9.1, les parcelles de matière 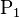 ,
, 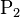 ,
, 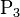 et
et 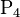 contiennent des points situés sur des surfaces de discontinuité : deux frontières séparant deux milieux différents.
Quelle que soit la dimension d'une parcelle contenant un point situé sur une surface de discontinuité, la masse volumique de cette parcelle dépendra de la position qu'elle occupe par rapport à la surface de discontinuité.
Donc, aucune masse volumique ne peut être définie en des points situés sur une surface de discontinuité.
contiennent des points situés sur des surfaces de discontinuité : deux frontières séparant deux milieux différents.
Quelle que soit la dimension d'une parcelle contenant un point situé sur une surface de discontinuité, la masse volumique de cette parcelle dépendra de la position qu'elle occupe par rapport à la surface de discontinuité.
Donc, aucune masse volumique ne peut être définie en des points situés sur une surface de discontinuité.
- Fig.9 : Surfaces de discontinuité
-

1. Récipient
-

2. Porte vénitienne
Particule matérielle
Afin que la masse volumique d'une parcelle de matière soit une fonction continue qui puisse rendre compte, de la répartition de la masse, avec une précision suffisante, il est nécessaire que la valeur du volume de cette parcelle soit comprise entre la valeur du volume 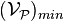 et celle du volume
et celle du volume 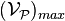 .
Cette parcelle de matière sera nommée particule matérielle.
La masse volumique d'une particule matériel sera désignée par
.
Cette parcelle de matière sera nommée particule matérielle.
La masse volumique d'une particule matériel sera désignée par 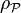 .
.
Si la matière est incompressible, la masse volumique d'une particule matérielle sera celle du corps.
Masse volumique mathématique
La masse volumique intervient notamment dans les équations fondamentales de la Mécanique.
Cette masse volumique ne peut être que la masse volumique d'une quantité fictive de matière qui se trouverait à l'intérieur d'un espace infiniment petit.
C'est pourquoi nous l'appelons masse volumique mathématique.
Nous la désignerons par la lettre 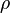 .
Un corps de matière solide ou fluide peut être assimilé à un domaine continu de points géométriques.
La masse volumique mathématique
.
Un corps de matière solide ou fluide peut être assimilé à un domaine continu de points géométriques.
La masse volumique mathématique 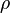 est attribuée à un point de ce domaine continu de points géométriques.
La masse volumique mathématique est, en un point de ce domaine, la masse volumique d'une parcelle infiniment petite, de masse
est attribuée à un point de ce domaine continu de points géométriques.
La masse volumique mathématique est, en un point de ce domaine, la masse volumique d'une parcelle infiniment petite, de masse 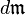 et de volume
et de volume 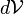 , contenant ce point ( masse volumique ponctuelle).
En désignant par
, contenant ce point ( masse volumique ponctuelle).
En désignant par 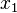 ,
, 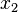 et
et 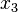 les coordonnées d'un point
les coordonnées d'un point  de ce domaine, nous pouvons définir, la masse volumique ponctuelle
de ce domaine, nous pouvons définir, la masse volumique ponctuelle 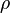 d'une parcelle infiniment petite contenant ce point, de la manière suivante :
d'une parcelle infiniment petite contenant ce point, de la manière suivante :
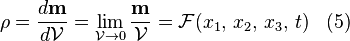 .
.
Pour qu'elle soit une grandeur définie en un point d'un domaine, la masse volumique mathématique 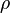 doit être une fonction continue en ce point.
C'est-à-dire que les masses volumiques de toutes les parcelles, de volumes infiniment petits contenant toutes un même point
doit être une fonction continue en ce point.
C'est-à-dire que les masses volumiques de toutes les parcelles, de volumes infiniment petits contenant toutes un même point  d'un domaine, doivent avoir des valeurs identiques : les masses volumiques mathématiques des deux parcelles
d'un domaine, doivent avoir des valeurs identiques : les masses volumiques mathématiques des deux parcelles 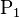 et
et 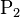 sont donc égales (figure 1.4).
Nous dirons alors que la distribution de la masse est continue dans le voisinage du point
sont donc égales (figure 1.4).
Nous dirons alors que la distribution de la masse est continue dans le voisinage du point  .
Dans ces conditions, la masse
.
Dans ces conditions, la masse 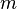 d'un corps peut être exprimée, en fonction de la masse volumique mathématique
d'un corps peut être exprimée, en fonction de la masse volumique mathématique 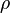 et du volume
et du volume 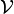 de ce corps, grâce à l'intégrale de volume suivante :
de ce corps, grâce à l'intégrale de volume suivante :
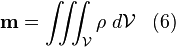 .
.
La masse volumique mathématique intervient dans les équations ponctuelles fondamentales de la mécanique. En mécanique des fluides, ce sont, par exemple :
- L'équation ponctuelle de la conservation de la masse :
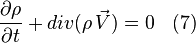 .
.
- L'équation ponctuelle de la dynamique :
 .
.
Des équations dans lesquelles interviennent aussi d'autres grandeurs ponctuelles attribuées au point  : le vecteur vitesse
: le vecteur vitesse 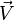 , la pression
, la pression 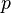 , le vecteur accélération
, le vecteur accélération  de la pesanteur et la force de frottement visqueux
de la pesanteur et la force de frottement visqueux 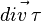 .
.
En mécanique du point, une masse est attribuée à un seul point que l'on assimile à tout un corps : il s'agit de l'entité mathématique point-masse ou point matériel. Dans le cas où c'est une masse volumique ponctuelle qui est attribuée à un point d'un domaine continu de points géométriques, nous pourrions envisager qu'il s'agit là d'une entité mathématique que nous pourrions qualifier de point-masse volumique ou de particule mathématique ; celle-ci appartiendrait à un domaine continu de points-masse volumique dont chaque point coïnciderait avec un point d'un domaine continu de points géométriques. Particule matérielle désignerait alors l'entité physique constituée d'un point géométrique auquel on attribue une masse volumique moyenne qui, à l'échelle d'un corps, peut être considérée comme une masse volumique ponctuelle.
Masse volumique mathématique et masse volumique physique
La masse volumique mathématique 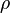 est une grandeur ponctuelle représentant la masse volumique d'une quantité fictive de matière située à l'intérieur d'un espace infiniment petit.
La masse volumique
est une grandeur ponctuelle représentant la masse volumique d'une quantité fictive de matière située à l'intérieur d'un espace infiniment petit.
La masse volumique 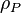 d'une particule matérielle est une grandeur physique moyenne représentant la masse volumique d'une quantité réelle de matière située à l'intérieur d'un espace considérée comme infiniment petit à l'échelle d'un corps.
d'une particule matérielle est une grandeur physique moyenne représentant la masse volumique d'une quantité réelle de matière située à l'intérieur d'un espace considérée comme infiniment petit à l'échelle d'un corps.
La masse d'une particule matérielle est égale à :
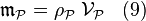 .
.
Cette masse peut aussi être exprimée en considérant la masse volumique 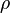 :
:
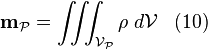 .
.
En égalant (9) et (10) et en réalisant un développement limité à l'ordre 4 de l'intégrale, nous obtenons une relation entre 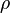 et
et  [12] :
[12] :
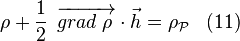
où les composantes du vecteur 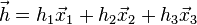 sont les dimensions d'une particule matérielle selon les axes respectifs
sont les dimensions d'une particule matérielle selon les axes respectifs 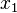 ,
, 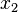 et
et 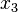 d'un repère.
d'un repère.
Notes et références
- ↑ Calecki Daniel, Physique des milieux continus, Tome 1 Mécanique et thermodynamique, Éd. Hermann, 2007, p. 17
- ↑ Sudhakar Nair, Introduction to Continuum Mechanics, Cambridge University Press, 2009, p. 2
- ↑ Roy Maurice. Cours de mécanique des milieux continus. Tome 2, Éd. Dunod. 1965. p. 4
- ↑ Mandel J., Cours de mécanique des milieux continus, tome 1. Gauthier-Villars, 1966. p. 1
- ↑ Lemaitre Jean, Chaboche Jean-Louis. Mécanique des matériaux solides. Éd. Dunod. 1985. p. 72
- ↑ Coirier Jean. Mécanique des milieux continus. Éd. Dunod. 1997. p. 5
- ↑ Thionnet Alain, Martin Christiane, Mécanique et comportement des milieux continus, Éd. Ellipses, 2003. p. 7
- ↑ Brun Edmond, Martinot-Lagarde, Mathieu Jean, Mécanique des fluides, Éd. Dunod, 1997. p. 14
- ↑ Chassaing Patrick, Mécanique des fluides. Cépaduès-Éditions. 1997. p. 5
- ↑ Cousteix Jean. [PDF] Voir chapitre Courtes citations
- ↑ Lesieur Marcel, La turbulence. Presses Universitaires de Grenoble. 1994. p. 29
- 1 2 3 [PDF] Lézé-Lerond Fabrice, Fascicule Masse volumique, tableau Domaine discontinu, lire Fascicules de Physique
- Portail de la physique