Mètre
| Mètre | |
 La barre de l'alliage de platine-iridium utilisée comme étalon du mètre de 1889 à 1960. |
|
| Informations | |
|---|---|
| Système | Unités de base du système international |
| Unité de... | Longueur |
| Symbole | m |
| Conversions | |
| 1 m en... | est égal à... |
| Unités US | 3,28084 pieds |
| 39,3701 pouces | |
| modifier | |
Le mètre (symbole m, du grec ancien μέτρον, métron mesure[1]) est l'unité de base de longueur du système international (SI). Il est défini, depuis 1983, comme la distance parcourue par la lumière dans le vide en 1/299 792 458 seconde[2].
Historique
Au début de l'ère chrétienne, une relative uniformité des unités de longueur avait régné, dans le bassin méditerranéen, grâce à la suprématie de l'Empire romain qui avait imposé de fait le pied romain.
Avec la décadence puis le morcellement de l'Empire romain, chaque peuple a progressivement défini une unité de mesure de longueur adapté à sa région ou à son activité.
Plusieurs projets d'unification, lancés par divers monarques, n'ont pu mettre fin à ces pratiques locales[3].
Prémices d'une définition universelle
En 1668, John Wilkins publie la description d'une « mesure de longueur universelle », d'une unité de mesure dans le système décimal et qui serait la longueur d'un pendule qui oscille avec un battement d'une seconde, soit une période de 2 secondes. Sa longueur fondamentale est de 38 pouces de Prusse (1 pouce prussien = 26,15 mm), soit 993,7 mm. Dans ce même ouvrage, il en déduit la mesure du litre et du kilogramme, même si elles ne sont pas nommées ainsi[4].
Sept ans plus tard, Tito Livio Burattini publie Misura Universale, ouvrage dans lequel il renomme la mesure universelle de Wilkins en metro cattolico (littéralement « mesure catholique » c'est-à-dire « universelle ») et confirme sa définition.
Il faudra cependant attendre plus d'un siècle pour que le mètre soit adopté et son usage généralisé par l'esprit des Lumières et de la Révolution française. Auparavant, les longueurs étaient mesurées en référence à l'humain (le pouce, le pied, la toise) ; comme chaque être humain est différent, on prenait souvent comme référence le roi, ce qui était un symbole monarchique fort. En pleine période révolutionnaire, en France, il fut donc décidé, afin de supprimer toute référence à un homme particulier et pour faciliter la diffusion du savoir, de choisir un étalon non humain unique et d'utiliser des multiples et sous-multiples de 10. Fini ainsi le pied qui valait 12 pouces.
Une longue série de tentatives va ainsi être concrétisée par l'adoption à l'Assemblée nationale, le , de deux décrets (signés par le roi Louis XVI, le 22 août) relatifs au projet d'unification des poids et mesures, proposé par Charles-Maurice de Talleyrand-Périgord, permettant le début des travaux d'une commission de l'Académie française des sciences[5].
Première définition du mètre
Le rapport de l'Académie des sciences du — présenté par Nicolas de Condorcet — préconisait, parmi les propositions de Jean-Charles de Borda, que l'unité de longueur, baptisée mètre, soit basée sur une distance correspondant à une partie de l'arc du méridien terrestre[5]. Elle suggérait aussi que « l'on mesure, non pas tout un quart de méridien, mais l'arc de neuf degrés et demi entre Dunkerque et Montjuïc (Barcelone), qui se trouve exactement de part et d'autre du 45e parallèle et dont les extrémités sont au niveau de la mer[5]. »
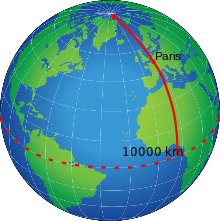
Le mètre est défini officiellement le par l'Académie des sciences comme étant la dix-millionième partie de la moitié de méridien terrestre (ou d'un quart de grand cercle passant par les pôles), ou encore le dix-millionième de la distance pour aller par le plus court chemin d’un pôle à un point donné de l’équateur[3]. Il s'avère que cette grandeur est quasiment identique au mètre du pendule défini à une latitude de 45° et au niveau de la mer, puisque celui-ci valait 0,993977 m de la nouvelle unité[6],[N 1].
Si ce n'est le corps humain, la nature restait donc la référence ; bien que la définition de Burattini aurait pu s'avérer plus précise, la définition du mètre par rapport à la longueur d’un chemin fut jugée plus compréhensible que celle d’un pendule liée à la définition de la seconde mais aussi à d'autres grandeurs comme la pesanteur[6], [N 2].
Toutefois, cette définition géophysique ne permettait pas de concrétiser le mètre pour le légaliser. En , Jean-Baptiste Joseph Delambre fut chargé de mesurer la distance entre Dunkerque et Rodez pendant que Pierre Méchain mesura celle de Barcelone à Rodez. Ils devaient se retrouver à Rodez. Cela devait permettre d'établir précisément et concrètement la valeur du mètre.
En 1793, à Montjuïc près de Barcelone, Méchain détecta une incohérence entre les longueurs relevées et le relevé astronomique de la position des étoiles. La guerre franco-espagnole l'empêcha de réitérer ses mesures. Cet écart, qui n'était en fait pas dû à une erreur de manipulation mais à l'incertitude des instruments utilisés[N 3], le plongea dans un profond trouble et il mit tout en œuvre pour éviter de devoir rendre compte de ses travaux à Paris.
En août 1793, la Convention nationale décréta que le système nouveau des poids et mesures se substituerait à l'ancien pour toute la République française.
C’est finalement la mesure de Delambre qui fut adoptée par la France le comme mesure de longueur officielle[7],[6].

De à , seize mètres-étalons gravés dans du marbre furent placés dans Paris et ses alentours, pour familiariser la population avec la nouvelle mesure. Aujourd'hui, il n'en subsiste que quatre :
- l'un est au 36 de la rue de Vaugirard, à droite de l'entrée ;
- le deuxième, replacé en 1848, est au 13 de la place Vendôme, à gauche de l'entrée du ministère de la Justice,
- le troisième est à Croissy-sur-Seine (Yvelines), dans un mur de la rue au Mètre[N 5],
- le quatrième à Sceaux (Hauts-de-Seine).
En 1799, Méchain se résigne à se rendre à une conférence internationale qui salue son œuvre scientifique. Il maquille alors ses résultats, ce qui rend le mètre-étalon de 1795 trop court de 0,2 mm par rapport à sa définition initiale de 1791 donnée par l’Académie des sciences. Ainsi en 1799, un nouveau mètre-étalon en platine fut créé à partir de cette définition et devint la référence (loi du 19 frimaire an VIII)[8]. La « fraude » de Méchain ne sera découverte par Delambre qu'en 1806, année où il réétudiera l'ensemble des résultats lors de la rédaction de Base du système métrique, sans pour autant renier ce nouveau mètre-étalon qui ne correspondait plus à la définition de 1791 de l’Académie des sciences. Ce second mètre-étalon (qui sera utilisé pendant 90 ans, soit la plus longue période légale pour ce mètre) ne correspondait donc déjà plus à la Terre.
Le système métrique décimal est officiellement adopté en France par la loi du qui favorise la connaissance à l'étranger de ce système. Avant même d'y être officiellement adopté, il est progressivement utilisé aux Pays-Bas en 1816, en Grèce en 1836, en Espagne en 1849, en Italie en 1850, aux États-Unis en 1866, en Allemagne en 1868, au Canada en 1871, etc.[9]
Le premier mètre étalon du BIPM
En 1889, le Bureau international des poids et mesures (BIPM) redéfinit le mètre comme étant la distance entre deux points sur une barre d'un alliage de platine et d'iridium. Cette barre (la troisième concrétisation légale du mètre-étalon) est toujours conservée au pavillon de Breteuil à Sèvres[10].
Cette concrétisation du mètre s'avérera vite assez peu compatible avec les progrès réalisés et avec les besoins de précision demandés par le milieu scientifique. Celui-ci s'inquiète déjà des conditions de conservation de ce mètre légal également difficile à reproduire en laboratoire, le mètre-étalon légal n’étant pas assez accessible pour permettre des mesures comparatives précises sans en même temps en altérer irrémédiablement ses propriétés physiques.
Définitions modernes
En 1960, la 11e Conférence générale des poids et mesures (CGPM) redéfinit le mètre comme 1 650 763,73 longueurs d'onde d'une radiation orangée émise par l'isotope 86 du krypton[11].
La 17e CGPM de 1983 redéfinit la vitesse de la lumière dans le vide absolu à 299 792 458 m/s, ce qui a pour effet de réviser la valeur du mètre comme étant la distance parcourue par la lumière dans le vide en 1/299 792 458 seconde[2],[3].
La vitesse de la lumière dans le vide étant la même en tous points (résultat établi par l'expérience de Michelson-Morley et ayant servi de base à la relativité restreinte), la définition de 1983 est plus précise que l'antérieure car la seconde est l'unité du Système international (SI) qui est mesurée avec la plus faible incertitude[11],[2].
Conversions et repères
Relation avec d'autres unités de mesures
Il existe une relation entre l'unité de mesure (mètre), l'unité de masse (kilogramme), les unités de surface (mètre carré) et les unités de volume (mètre cube et litre, souvent utilisés pour désigner des volumes ou des quantités de liquides) :
- un mètre carré (m2) est, par exemple, la surface d'un carré dont chaque côté mesure un mètre ;
- un mètre cube (m3) est, par exemple, le volume d'un cube dont chaque arête mesure un mètre ;
- à l'origine, le kilogramme fut défini comme la masse d'un décimètre cube (dm3) d'eau pure, avant d'être remplacé par un étalon en platine d’un kilogramme (voir : Historique du kilogramme).
Dans certains métiers (terrassement, de construction, etc.), on parle de « mètre linéaire (noté : « ml »). Il s'agit d'un pléonasme, puisque le mètre désigne précisément une longueur de ligne et que la norme NF X 02-003[12] précise qu'on ne doit pas affecter les noms d'unités de qualificatifs qui devraient se rapporter à la grandeur correspondante. Par ailleurs le symbole mℓ ou mL correspond dans le SI à millilitre, ce qui n'a rien à voir avec une longueur et est une source de confusion.
On emploie usuellement pour les gaz le normo mètre cube, anciennement noté « mètre cube normal », qui correspond au volume mesuré en mètres cubes dans des conditions normales de température et de pression. Cette unité n'est pas reconnue par le BIPM. Sa définition varie selon les pays et selon les professions qui l'utilisent.
En fait, et de façon générale, « le symbole de l’unité ne doit pas être utilisé pour fournir des informations spécifiques sur la grandeur en question. Les unités ne doivent jamais servir à fournir des informations complémentaires sur la nature de la grandeur ; ce type d’information doit être attaché au symbole de la grandeur et pas à celui de l’unité[13] » (ici le volume). On doit donc dire « volume mesuré en mètres cubes dans les conditions normales de température et de pression », abrégé en « volume normal en mètres cubes ».
Correspondance avec d'autres unités de longueur
Le mètre correspond à :
- 5,399 568.10−4 milles marins ;
- 6,215 04.10−4 miles terrestres ;
- 1,056 97.10−16 années-lumière ;
- 1,093 6 yard ;
- 3,281 pieds ;
- 39,37 pouces.
Quelques points de repères
- La taille d'un pied est d'environ 0,30 m.
- On parcourt environ 5 000 m en une heure de marche rapide.
- Un grand pas fait environ un mètre.
- Un pendule de 1 mètre de long effectue une oscillation complète (un aller-retour) en environ 2,0 secondes.
Multiples et sous-multiples du mètre
| 10N | Nom préfixé | Symbole | Nombre en français | Nombre en mètres |
|---|---|---|---|---|
| 1024 | yottamètre | quadrillion | 1 000 000 000 000 000 000 000 000 | |
| 1021 | zettamètre | trilliard | 1 000 000 000 000 000 000 000 | |
| 1018 | examètre | trillion | 1 000 000 000 000 000 000 | |
| 1015 | pétamètre | billiard | 1 000 000 000 000 000 | |
| 1012 | téramètre | billion | 1 000 000 000 000 | |
| 109 | gigamètre | milliard | 1 000 000 000 | |
| 106 | mégamètre | million | 1 000 000 | |
| 103 | kilomètre | mille | 1 000 | |
| 102 | hectomètre | cent | 100 | |
| 101 | décamètre | dix | 10 | |
| 100 | mètre | un | 1 | |
| 10-1 | décimètre | dixième | 0,1 | |
| 10-2 | centimètre | centième | 0,01 | |
| 10-3 | millimètre | millième | 0,001 | |
| 10-6 | micromètre | millionième | 0,000 001 | |
| 10-9 | nanomètre | milliardième | 0,000 000 001 | |
| 10-12 | picomètre | billionième | 0,000 000 000 001 | |
| 10-15 | femtomètre | billiardième | 0,000 000 000 000 001 | |
| 10-18 | attomètre | trillionième | 0,000 000 000 000 000 001 | |
| 10-21 | zeptomètre | trilliardième | 0,000 000 000 000 000 000 001 | |
| 10-24 | yoctomètre | quadrillionième | 0,000 000 000 000 000 000 000 001 |
| 10N | Nom préfixé | Symbole | Nombre en français | Nombre en mètres |
|---|---|---|---|---|
| 104 | myriamètre | dix mille | 10 000 | |
| 10-4 | myriomètre | dix millième | 0,000 1 |
Description de multiples
De fait, au-delà du milliard de kilomètres on utilise rarement l'unité standard : on lui préfère l'unité astronomique (ua), d'où est déduite l'unité dérivée, le parsec : ceci était nécessaire pour ne pas dénaturer les mesures précises de distance de parallaxe par une réévaluation de l'ua, liée à la valeur de la constante gravitationnelle (G). Cette situation peu œcuménique a été levée par les mesures directes par écho radar sur les planètes.
- Décamètre
- 1 dam = 10 m.
- Cette unité est adaptée au calcul de la superficie d'un terrain, par le biais de l'are, superficie, par exemple, d'un carré d'un décamètre de côté.
- Hectomètre
- 1 hm = 100 m.
- Cette unité est adaptée au calcul de la superficie d'une terre agricole, par le biais de l'hectare, superficie, par exemple, d'un carré d'un hectomètre de côté.
- Kilomètre
- 1 km = 1 000 m.
- C'est le multiple du mètre le plus fréquemment utilisé pour mesurer les distances terrestres (comme entre les villes). Le long des routes, les bornes kilométriques sont placées tous les kilomètres.
- Myriamètre
- 1 mam = 10 000 m.
- Il équivaut à 10 km. Cette unité est obsolète.
- Mégamètre
- 1 Mm = 1×106 m = 1 000 000 m.
- C'est une unité de mesure adaptée pour le diamètre des planètes. La Terre mesure par exemple environ 12,8 mégamètres de diamètre.
- Il équivaut à 1 000 km, soit 1×103 km.
- Gigamètre
- 1 Gm = 1×109 m = 1 000 000 000 m.
- C'est un multiple du mètre utilisé pour mesurer les distances interplanétaires courtes, par exemple entre une planète et ses satellites naturels. La Lune orbite à 0,384 gigamètre de la Terre (environ 1,3 seconde-lumière).
- On peut également s'en servir pour exprimer le diamètre des étoiles (environ 1,39 gigamètres pour le Soleil).
- Une unité astronomique représente approximativement 150 gigamètres.
- Il équivaut à 1 million de kilomètres, soit 1×106 km.
- Téramètre
- 1 Tm = 1×1012 m = 1 000 000 000 000 m.
- C'est un multiple du mètre utilisé pour mesurer les grandes distances interplanétaires. Par exemple la planète naine Pluton orbite à une moyenne de 5,9 téramètres du Soleil.
- Il équivaut à 1 milliard de kilomètres, soit 1×109 km.
- Pétamètre
- 1 Pm = 1×1015 m = 1 000 000 000 000 000 m.
- Une année-lumière vaut environ 9,47 Pm
- Proxima Centauri, l'étoile la plus proche, est située à environ 40 pétamètres du Soleil.
- C'est une bonne unité de mesure de la taille des nébuleuses.
- Examètre
- 1 Em = 1×1018 m = 1 000 000 000 000 000 000 m.
- Un examètre représente environ 106 années-lumière.
- Un amas globulaire mesure environ un examètre de diamètre.
- C'est une distance interstellaire typique dans la périphérie galactique.
- Zettamètre
- 1 Zm = 1×1021 m = 1 000 000 000 000 000 000 000 m.
- Un zettamètre représente environ 105 700 années-lumière.
- La Voie lactée (notre galaxie) mesure à peu près cette taille, une vingtaine de zettamètres la sépare de la galaxie d'Andromède.
- Yottamètre
- 1 Ym = 1×1024 m = 1 000 000 000 000 000 000 000 000 m.
- Un yottamètre représente environ 105,7 millions d'années-lumière.
- C'est une bonne unité de mesure des distances entre galaxies lointaines ou pour la taille des superamas.
- Les objets les plus lointains de l'Univers sont situés à environ 130 yottamètres. z8 GND 5296, découverte en 2013, serait la galaxie la plus éloignée de la nôtre[15] et la plus vieille actuellement connue. En effet, elle se situe à 13,1 milliards d'années-lumière soit environ 124 yottamètres.
Description des sous-multiples
- Décimètre
- 1 dm = 0,1 m.
- Au cours du XXe siècle, la règle graduée standard des écoliers était le double-décimètre (2 dm = 20 cm) et les programmes scolaires se référaient à cette appellation.
- Centimètre
- 1 cm = 0,01 m.
- Le centimètre est une des unités de base du système CGS.
- Millimètre
- 1 mm = 1×10-3 m = 0,001 m.
- Une représentation graphique manuelle précise nécessite l'utilisation de papier millimétré.
- Micromètre
- 1 µm = 1×10-6 m = 0,000 001 m.
- Le micromètre était autrefois appelé « micron » (symbole : µ). L'utilisation du terme « micron » a été bannie par la 13e CGPM en 1968.
- Cette unité est utilisée pour exprimer la taille des cellules.
- Nanomètre
- 1 nm = 1×10-9 m = 0,000 000 001 m.
Le nanomètre est utilisé pour mesurer les longueurs d'ondes plus courtes que celle de l'infrarouge (visible, ultraviolet et rayons X) et la finesse de gravure d'un microprocesseur. La limite théorique qui fait la frontière entre le micro-électronique et la nanoélectronique est une finesse de gravure de 100 nm. Les rayons atomiques varient entre 0,025 et 0,2 nm. Le nanomètre est aussi l'unité de mesure traditionnelle de la rugosité, contrôle de l'état de surface (métrologie dimensionnelle)
- Les virus mesurent quelques dizaines ou centaines de nanomètres.
- Picomètre
- 1 pm = 1×10-12 m = 0,000 000 000 001 m.
- Cette unité est de plus en plus utilisée pour mesurer les longueurs des liaisons atomiques à la place de l'ångström. 1Å = 100 pm.
- Femtomètre
- 1 fm = 1×10-15 m = 0,000 000 000 000 001 m.
- Le femtomètre fut d'abord nommé « fermi » en l'honneur du physicien italien Enrico Fermi (le fermi comme tel ne fait pas partie du Système international).
- Le femtomètre est fréquemment utilisé pour mesurer le diamètre d'un noyau atomique. Le diamètre d'un noyau atomique peut aller jusqu'à 15 fm.
- Attomètre
- 1 am = 1×10-18 m = 0,000 000 000 000 000 001 m.
- La taille maximale d'un quark est estimée à un attomètre.
- Zeptomètre
- 1 zm = 1×10-21 m = 0,000 000 000 000 000 000 001 m.
- Cette unité a un intérêt croissant au sein de la communauté scientifique. En effet, le domaine de l'infiniment petit étant en plein essor, des unités de plus en plus petites sont utilisées, par exemple dans le cadre de l'étude des particules.
- Yoctomètre
- 1 ym = 1×10-24 m = 0,000 000 000 000 000 000 000 001 m.
- Un yoctomètre est 62 milliards de fois supérieur à la longueur de Planck
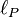 = 1,616252×10-35 m = 0,000 000 000 000 000 000 000 000 000 000 000 016 m.
= 1,616252×10-35 m = 0,000 000 000 000 000 000 000 000 000 000 000 016 m.
Multiples sans préfixes
- Ångström
- 1 Å = 1×10-10 m = 0,000 000 000 1 m.
- Cette unité de mesure, qui ne fait pas partie du Système international, est anciennement utilisée pour mesurer les rayons atomiques. Pour en savoir plus, voir l'article Ångström.
Notes et références
Notes
- ↑ La longueur du quadrant ou du demi-méridien était donc de 10 060 km en unités pendulaires. Elle est actuellement d'environ 10 002 km sur l'ellipsoïde WGS 84.
- ↑ Mais la définition de Burattini ne sera pas retenue alors car la période d’oscillation du pendule dépend de l’écart angulaire de cette oscillation que cette définition omet de préciser (elle suppose seulement un faible écart angulaire pour que les différences de périodes mesurées ne soient pas sensibles, et que cette oscillation soit entretenue, comme dans les horloges pendulaires, pour conserver cet écart angulaire afin que cette même période ne varie pas), ainsi que de la latitude et de l'altitude du lieu.
- ↑ Cette incertitude est liée à l'usure des instruments utilisés et à la réfraction de l'atmosphère lorsqu'il visait une étoile trop basse sur l'horizon ce que Méchain ne pouvait pas savoir à cette époque.
- ↑ Le seul à être resté à son emplacement d’origine parmi les seize implantés à Paris entre février 1796 et décembre 1797. Cette décision de la Convention nationale était destinée à généraliser l'usage du système métrique.
- ↑ Depuis 1996, l'original est conservé aux archives municipales de Croissy, il est remplacé par une copie in situ.
Références
- ↑ « Étymologie de mètre », sur le CNRTL.
- 1 2 3 « Résolution 1 de la 17e réunion de la CGPM (1983) – Définition du mètre », sur le site du Bureau international des poids et mesures, bipm.org.
- 1 2 3 Denis Février, « Histoire du mètre », sur Direction générale de la compétitivité de l'industrie et des services (consulté le 5 octobre 2013).
- ↑ (en) John Wilkins, An Essay towards a Real Character and a Philosophical Language, Royal Society, (lire en ligne), chap. VIII, p. 191-192.
- 1 2 3 « Talleyrand et l’établissement du système métrique », sur talleyrand.org (consulté le 30 juillet 2013).
- 1 2 3 Jacques-Paul Migne, Encyclopédie théologique, Dictionnaire des inventions et découvertes, vol. 36, , 1417 p. (lire en ligne), p. 417-419.
- ↑ Suzanne Débarbat et Antonio E. Ten, Mètre et système métrique, Observatoire de Paris, Université de Valence, , 194 p. (ISBN 84-370-1174-4, lire en ligne), p. 58, 191.
- ↑ L'aventure du mètre, Musée national des techniques, Conservatoire national des arts et métiers, Paris, 1989.
- ↑ Dominique Frémy, Michèle Frémy, Quid, Paris, Robert Laffont, 2007 (ISBN 978-2221106778), p. 245.
- ↑ « Le BIPM et l'évolution de la définition du mètre », sur Bureau international des poids et mesures (consulté le 5 octobre 2013).
- 1 2 « Du mètre et du kilogramme », sur metrodiff.org.
- ↑ « Afnor FD X 02-003, § 6.3, mai 2013 – Normes fondamentales – Principes de l'écriture des nombres, des grandeurs, des unités et des symboles », sur afnor.org, Afnor (consulté le 16 novembre 2013).
- ↑ « Le Système international d'unités 8e édition, 2006 – § 5.3.2 Symboles des grandeurs et des unités », sur bipm.org, Bureau international des poids et mesures (consulté le 23 mars 2014), p. 44 [PDF].
- ↑ (en) Measures, The Edinburgh Encyclopedia.
- ↑ (en) « Z8-GND-5296: Most Distant Galaxy Yet Discovered », sur Sci-News.com, (consulté le 7 avril 2014).
Bibliographie
- Denis Guedj, Le Mètre du monde, Éditions du Seuil, 2000, 330 p. (ISBN 2-02-040718-3 et 978-2020407182).
- L'Aventure du mètre, Musée national des techniques, Conservatoire national des arts et métiers, 1989, 103 p.
Annexes
Articles connexes
- Ordre de grandeur (longueur)
- Géodésie
- Géomètre
- Nanoparticule, nanomatériaux
- Nanométrologie
Liens externes
- Histoire du mètre, par la Direction générale des entreprises (DGE) (Consulté le 18-10-2015).
- L'Histoire du Mètre, site complet sur l'histoire du mètre, de la Révolution à nos jours.
- La convention du mètre qui instituera le BIPM, institution initiatrice du système international d'unités.
- Portail des mathématiques
- Portail de la géométrie
- Portail de la physique