Diamètre

Diamètre d'un cercle

Dans un cercle ou une sphère, le diamètre est un segment de droite passant par le centre et limité par les points du cercle ou de la sphère. Le diamètre est aussi la longueur de ce segment. Pour indiquer qu'une valeur correspond au diamètre, en technique, la valeur (du diamètre) est précédée par un symbole « ⌀ » (U+2300) représentant un cercle barré. Et ce symbole est lui-même précédé par la lettre S, s'il s'agit d'une sphère.^{[réf. nécessaire]}

Plus généralement dans un espace métrique (E, d) on appelle diamètre d'une partie non vide A la borne supérieure (dans l'ensemble ordonné [–∞, +∞]) des distances entre deux points de A :

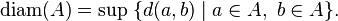
Ainsi, le diamètre d'une partie non vide est un réel positif si cette partie est bornée et vaut +∞ sinon^[1],[2].

Exemples

• Dans le plan euclidien, le diamètre d'un rectangle est la longueur d'une diagonale.
• Les parties non vides de diamètre nul sont les singletons^[1].

Diamètre du vide

Certains auteurs^[3],[4] étendent la définition formelle ci-dessus au cas de la partie vide — ce qui donne diam(∅) = sup(∅) = –∞ — mais la plupart préfèrent s'abstenir de considérer ce cas^[1] ou poser, par convention^[2], diam(∅) = 0, ce qui revient à définir le diamètre d'une partie quelconque comme une borne supérieure non pas dans [–∞, +∞] mais dans [0, +∞].

En astronomie, à la notion de diamètre on peut associer celle de diamètre apparent. Le diamètre apparent est alors homogène à un angle et se mesure en degrés ou en radians.

Notes et références

Articles connexes

• Conjecture de Borsuk (de)
• Diamètre (théorie des graphes)
• Rayon
• Théorème de Jung

• Portail de la géométrie