Espace métrique

Cet article ne cite pas suffisamment ses sources (avril 2011).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » (modifier l'article, comment ajouter mes sources ?).

En mathématiques, un espace métrique est un ensemble au sein duquel une notion de distance entre les éléments de l'ensemble est définie. C'est un cas particulier d'espace topologique. On appelle espace métrisable un espace topologique homéomorphe à un espace métrique.

L'exemple correspondant le plus à notre expérience intuitive de l'espace est l'espace euclidien à trois dimensions. La métrique euclidienne de cet espace définit la distance entre deux points comme la longueur du segment les reliant.

La classe d'isométrie d'un espace métrique (c'est-à-dire l'ensemble de tous les espaces de même structure métrique) est beaucoup plus petite que sa classe d'homéomorphie. Par exemple un carré, un triangle, un cercle et n'importe quelle courbe de Jordan sont homéomorphes, par contre ils ne sont pas isométriques. Ainsi une structure métrique code beaucoup plus d'information sur la forme géométrique des objets qu'une simple structure topologique ; ce qui n'a rien de surprenant, car la notion de distance entre deux points est centrale pour la géométrie usuelle.

Définitions

On appelle (E, d) un espace métrique si E est un ensemble et d une distance sur E.
On appelle distance sur un ensemble E, une application d de E² dans ℝ⁺ telle que, pour tout x, y, z de E :
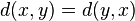- $d(x,y)=d(y,x)$ (symétrie) ;
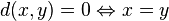- $d(x,y)=0\Leftrightarrow x=y$ (séparation) ;
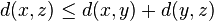- $d(x,z)\le d(x,y)+d(y,z)$ (inégalité triangulaire).
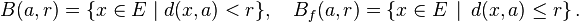
On appelle boule ouverte (resp. fermée) centrée en un point a de E et de rayon r (un élément de ℝ⁺), l'ensemble des points x situés à une distance de a strictement plus petite que r (resp. inférieure ou égale à r) : $B(a,r)=\{x\in E\mid d(x,a)<r \},\quad B_f(a,r)=\left\{x\in E\,\mid\,d(x,a)\leq r\right\}.$
On appelle ouvert de E, toute réunion de boules ouvertes.
Une partie U de E est donc un ouvert si et seulement si, pour tout x de U, il existe une boule ouverte contenant x (donc de rayon non nul) et incluse dans U (une telle boule peut alors toujours être choisie centrée en x car B(x, s) est incluse dans B(a, r) dès que s ≤ r – d(x, a)). L'ensemble de ces ouverts constitue alors une topologie sur E — dite « topologie induite par la distance » d — dont une base est l'ensemble des boules ouvertes (en effet, si un point x appartient à l'intersection de deux boules ouvertes alors B(x, s) est incluse dans cette intersection pour s assez petit). Dans cette topologie, les voisinages d'un point sont tous les sous-ensembles contenant une boule ouverte contenant ce point.
Un espace topologique est dit métrisable s'il existe une distance induisant sa topologie. La topologie usuelle sur la droite réelle, sur le plan, etc. sont des exemples de topologies métrisables. Les notions de boule, de partie bornée, de suite de Cauchy, de continuité uniforme, etc. ne sont pas des notions topologiques mais métriques, susceptibles de varier selon la distance choisie.

Remarques

Pour toute partie non vide A de E, l'application qui à tout point x de E associe la distance de x à A (c'est-à-dire l'inf des distances de x à tous les points de A) est continue car 1-lipschitzienne. Les x en lesquels elle s'annule sont les points adhérents à A.
- Tout espace topologique métrisable est par conséquent non seulement séparé mais parfaitement normal — donc normal — c'est-à-dire que tous les singletons sont fermés et que tout fermé F est le lieu d'annulation d'une fonction continue : l'application x ↦ d(x, F).
En particulier, pour tout élément a de E, l'application x ↦ d(x, a) est 1-lipschitzienne. On en déduit que :
- toute boule fermée B_f(a, r) est un fermé pour la topologie associée à la distance (comme image réciproque, par cette application, du fermé [0, r]). La notation B(a, r) est également utilisée mais ambigüe, car l'adhérence de B(a, r) est parfois strictement incluse dans B_f(a, r), même pour r > 0 : voir les articles « Boule (mathématiques) » et « Distance ultramétrique ».
- l'application d est 2-lipschitzienne, sur l'espace produit E×E muni de la distance d_$\infty$ définie par d_$\infty$((x₁, x₂), (y₁, y₂)) = max(d(x₁, y₁), d(x₂, y₂)).
Sur toute partie A de E, la topologie induite coïncide avec celle définie par la restriction de la distance. En effet, elles possèdent toutes les deux comme base de voisinages d'un point x de A l'intersection avec A des boules ouvertes de centre x.
Un espace métrique est dit propre si toutes ses boules fermées sont compactes. Tout espace métrique propre est localement compact mais la réciproque est fausse.

Exemples

Une norme N sur un espace vectoriel réel induit de manière naturelle une distance d(x, y) = N(x – y). Diverses distances usuelles sur ℝⁿ sont obtenues ainsi, par exemple :
- (pour n = 1) la distance usuelle sur l'ensemble des réels est celle associée à la valeur absolue ;
- (pour n = 2) la distance de Manhattan sur le plan ℝ² : d(a, b) = |x_b – x_a| + |y_b – y_a|. C'est la distance induite par la norme 1 ;
- (pour n = 2) la distance aux échecs permet de connaître le nombre minimum de coups au jeu d'échecs pour aller avec le roi d'une case a = (x_a, y_a) à une case b = (x_b, y_b) et se définit par : d(a, b) = max(|x_b – x_a|, |y_b – y_a|) ;
La distance triviale (ou encore distance discrète ou métrique discrète) est définie sur tout ensemble par : d(x, y) = 1 si x ≠ y et d(x, x) = 0. La topologie associée est la topologie discrète.
La distance de Hamming est utilisée en théorie des codes correcteurs.
Les espaces topologiques ℝ et ]0, 1[ sont homéomorphes mais, munis de la distance usuelle, ils ne sont pas isomorphes en tant qu'espaces métriques ; par exemple ℝ est complet mais ]0, 1[ ne l'est pas.
Si l'on munit ℝ⁺ de la distance d(x, y) = |e^x – e^y|, on retrouve la topologie usuelle sur ℝ⁺ mais maintenant toutes les fonctions polynômes sont uniformément continues.

Produit d'espaces métriques

Tout produit fini ou dénombrable d'espaces métriques peut être muni d'une distance qui induit la structure uniforme produit et a fortiori la topologie produit : pour cela, si les (E_k, d_k) (k∈ℕ) sont des espaces métriques, on peut par exemple munir E₁×…×E_n de la distance d_N définie par

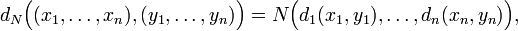
d_N\Big((x_1,\ldots,x_n),(y_1,\ldots,y_n)\Big)=N\Big(d_1(x_1,y_1),\ldots,d_n(x_n,y_n)\Big),

où N est une norme ℓ^p arbitraire sur ℝⁿ (ou toute autre norme croissante sur (ℝ⁺)ⁿ pour l'ordre produit) et munir E = ∏_k∈ℕE_k de la distance d définie par

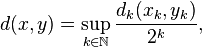
d(x,y)=\sup_{k\in\N}\frac{d_k(x_k,y_k)}{2^k},

où chaque distance sur E_k est au préalable remplacée si nécessaire par une distance équivalente d_k majorée par une constante indépendante de k. On vérifie facilement que d_N et d sont bien des distances sur les espaces correspondants et que la topologie définie par d_N coïncide avec la topologie produit. Démontrons qu'il en est de même pour la distance d sur E (les calculs montrent même que non seulement les deux topologies coïncident, mais aussi les deux structures uniformes dont elles sont issues, sous réserve d'avoir choisi, dans le remplacement préalable des d_k, des distances équivalentes uniformément et pas seulement topologiquement).

Égalité entre la topologie du produit dénombrable et la topologie associée à la distance

Supposons sans perte de généralité que toutes les distances d_k sont majorées par 1.

Tout ouvert de la prébase canonique du produit est, pour d, ouvert (c'est-à-dire voisinage de chacun de ses points) : un ouvert de la prébase est de la forme U = ∏_k∈ℕU_k où tous les U_k sont égaux aux E_k, sauf l'un d'entre eux, U_n, qui est seulement un ouvert de E_n. Soit a un point de U, alors a_n appartient à U_n donc pour r assez petit, la d_n-boule de centre a_n et de rayon r est incluse dans U_n. Ainsi, U est un voisinage de a pour d car il contient la d-boule de centre a et de rayon 2^–nr.
Tout ouvert O pour d est ouvert pour la topologie produit : soit a un point de O. Il existe r > 0 tel que la boule B(a, r) soit incluse dans O, puis n tel que 2^–n < r. Posons U = ∏_k∈ℕU_k avec U_k = B_k(a_k, 2^kr) pour 0 ≤ k ≤ n et U_k = E_k pour k > n. Alors, pour la topologie produit, U est un voisinage de a inclus dans B(a, r), donc O est un voisinage de a.

Si chaque d_k est la distance discrète, ce choix de d donne : si x ≠ y, d(x, y) = 2^–k où k est le plus petit n tel que x_n ≠ y_n. Des exemples sont l'espace de Baire et les anneaux topologiques de séries formelles.

En revanche, un produit non dénombrable d'espaces topologiques non grossiers n'est jamais métrisable, ni même séquentiel.

Équivalence d'espaces métriques

En comparant deux espaces métriques il est possible de distinguer différents degrés d'équivalence. Pour préserver a minima la structure topologique induite par la métrique, une fonction continue entre les deux est requise.

Deux espaces métriques (M₁, d₁) et (M₂, d₂) sont dits :

topologiquement isomorphes (ou homéomorphes) s'il existe un homéomorphisme entre eux ;
uniformément isomorphes s'il existe entre eux une bijection uniformément continue dont la réciproque est uniformément continue.
Lipschitz-équivalents s'il existe une bijection de l'un sur l'autre qui est lipschitzienne ainsi que son application réciproque.
isométriquement isomorphes s'il existe une isométrie bijective entre eux. Dans ce cas les deux espaces sont essentiellement identiques. Une isométrie est une fonction f : M₁ → M₂ qui préserve les distances : d₂(f(x), f(y)) = d₁(x, y) pour tout x, y dans M₁. Les isométries sont forcément injectives.
semblables s'il existe une constante positive k > 0 et une bijection f : M₁ → M₂, appelée similitude, telle que d₂(f(x), f(y)) = k d₁(x, y) pour tout x, y dans M₁.
similaires s'il existe une bijection f : M₁ → M₂, appelée similarité, telle que d₂(f(x), f(y)) = d₂(f(u), f(v)) si et seulement si d₁(x, y) = d₁(u, v) pour tous x, y, u, v dans M₁.^{[réf. souhaitée]}

Deux espaces euclidiens similaires sont nécessairement homéomorphes, donc de même dimension et par conséquent isométriques.

Espaces métrisables

Partant d'un espace topologique, on peut se demander s'il est métrisable. Plusieurs conditions suffisantes pour cela ont été trouvées.

La première réellement utile est due à Urysohn ; elle dit que tout espace régulier à base dénombrable est métrisable. (Cette forme de la condition a en fait été prouvée par Tychonov en 1926. Ce qu'Urysohn avait trouvé, dans un article publié en 1925, était que tout espace normal à base dénombrable est métrisable.) Par exemple, toute variété à base dénombrable est métrisable. Également un compact est métrisable si et seulement s'il est à base dénombrable.
Cette condition suffisante d'Urysohn (régularité + base dénombrable) a été transformée en une condition nécessaire et suffisante (régularité + base dénombrablement localement finie) par Bing, Nagata et Smirnov
Smirnov a aussi prouvé qu'un espace est métrisable si et seulement s'il est paracompact et localement métrisable (un espace est dit localement métrisable si chaque point a un voisinage métrisable). En particulier, une variété est métrisable si et seulement si elle est paracompacte.

Articles connexes

Espace à bases dénombrables de voisinages
Espace complet
Espace précompact
Espace pseudométrique
Espace quasimétrique
Espace uniforme
Géodésique
Plongement de Kuratowski
Topologie
Théorème de Bolzano-Weierstrass et autres critères de compacité pour un espace métrique
Espaces de longueur

Portail de la géométrie

This article is issued from Wikipédia - version of the Tuesday, August 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.