Arc de méridien
|
|
La traduction de cet article ou de cette section doit être revue. Le contenu est difficilement compréhensible vu les erreurs de traduction, qui sont peut-être dues à l'utilisation d'un logiciel de traduction automatique.
Discutez des points à améliorer en page de discussion ou modifiez l'article.
|
En géodésie, la mesure d'un arc de méridien est la détermination la plus exacte possible de la distance entre deux points situés sur un même méridien, soit à la même longitude. Deux ou plusieurs déterminations de ce type dans des endroits différents précisent ensuite la forme de l'ellipsoïde de référence qui donne la meilleure approximation de la forme du géoïde. Ce processus est appelé « déterminer la figure de la Terre ». Les premières mesures de la taille d'une Terre sphérique eurent besoin d'un seul arc. Les mesures les plus récentes utilisent des mesures astro-géodésiques et des méthodes de géodésie par satellite afin de déterminer l'ellipsoïde de référence.
Description mathématique
Un arc de méridien sur un ellipsoïde a la forme exacte d'une ellipse. Par conséquent, sa longueur entre l'équateur et un point à la latitude φ peut être calculée comme une intégrale elliptique et approchée par une série tronquée. Le développement suivant qui fait intervenir le carré de l'excentricité e a été donné par Jean-Baptiste Joseph Delambre en 1799[1]:
Friedrich Robert Helmert a utilisé la formule suivant en 1880[2], en posant 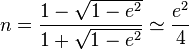 :
:
Kazushige Kawase a donné une formule générale en 2009[3],[4] :
dans laquelle 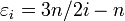 .
.
En tronquant la somme à j=2, on obtient la formule de Helmert.
Approximations
La distance polaire peut être approchée par la formule de Muir :
Notes et références
- ↑ Delambre, J. B. J. (1799): Méthodes Analytiques pour la Détermination d'un Arc du Méridien; précédées d'un mémoire sur le même sujet par A. M. Legendre, De L'Imprimerie de Crapelet, Paris, 72–73
- ↑ (de) Helmert, F. R. (1880): Die mathematischen und physikalischen Theorieen der höheren Geodäsie, Einleitung und 1 Teil, Druck und Verlag von B. G. Teubner, Leipzig, 44–48
- ↑ (ja) 河瀬和重 (Kawase, K.) (2009): 緯度を与えて赤道からの子午線弧長を求める一般的な計算式 (A General Formula for Meridional Distance from the Equator to Given Latitude), 国土地理院時報 (Journal of the Geographical Survey Institute), 119, 45–55
- ↑ (en) Kawase, K. (2011): A General Formula for Calculating Meridian Arc Length and its Application to Coordinate Conversion in the Gauss-Krüger Projection, Bulletin of the Geospatial Information Authority of Japan, 59, 1–13
Voir aussi
- Arc géodésique de Struve
- Expéditions géodésiques françaises
- Figure de la Terre et méridienne de Delambre et Méchain
- Portail de la géodésie et de la géophysique

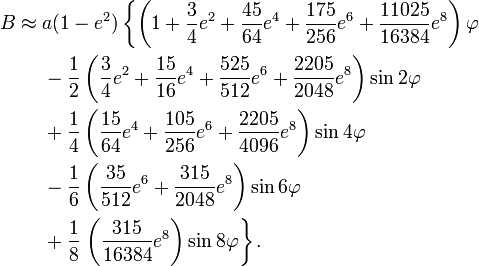
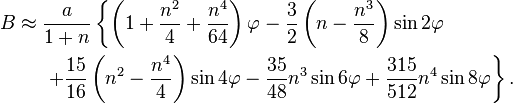
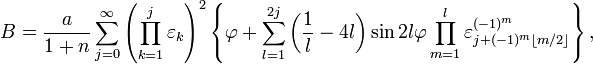
![m_p=\int_0^{\pi/2}\!M(\varphi)\,d\varphi\;\approx\frac\pi2\left[\frac{a^{3/2}+b^{3/2}}{2}\right]^{2/3}\,\!.](../i/m/21d0a2afee68671ea35e079525b4a2a3.png)