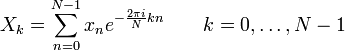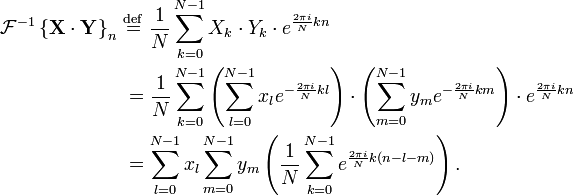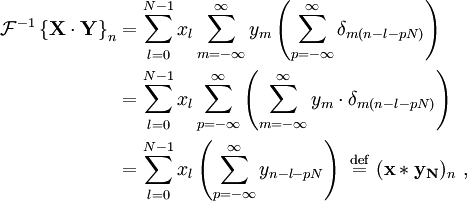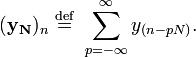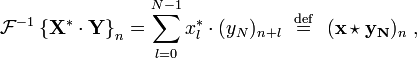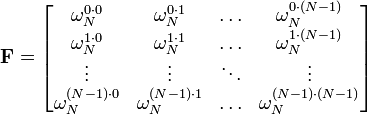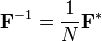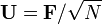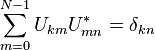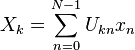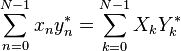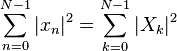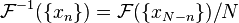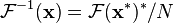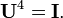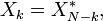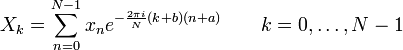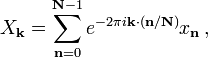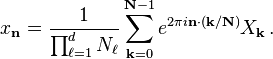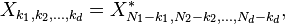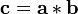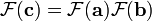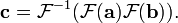Transform??e de Fourier discr??te
Contexte des ??coles Wikip??dia
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Parrainer un enfant de faire une r??elle diff??rence.
| transform??es de Fourier |
|---|
| Transform??e de Fourier en continu |
| s??rie de Fourier |
| Temps discret transform??e de Fourier |
| Transform??e de Fourier discr??te |
En math??matiques , la transform??e de Fourier discr??te (DFT) est l'une des formes sp??cifiques de analyse de Fourier. En tant que tel, il se transforme en une autre fonction, qui est appel?? le repr??sentation dans le domaine fr??quence, ou simplement la TFD, de la fonction d'origine (ce qui est souvent une fonction du dans le domaine temporel). Mais la DFT n??cessite une fonction d'entr??e qui est valeurs discr??tes et dont les non-z??ro ont une (finie) de dur??e limit??e. Ces entr??es sont souvent cr????es par ??chantillonnage d'une fonction continue, comme la voix d'une personne. Et, contrairement ?? la discret dans le temps ?? transform??e de Fourier (DTFT), on ??value seulement assez de composantes de fr??quence pour reconstruire le segment fini qui a ??t?? analys??. Sa transform??e inverse ne peut pas reproduire le domaine temporel enti??re, ?? moins que l'entr??e se trouve ??tre p??riodique (toujours). Par cons??quent, il est souvent dit que la DFT est une transformation pour l'analyse de Fourier des fonctions ?? temps discret finie domaine. Les fonctions de base de la d??composition sinuso??dales ont les m??mes propri??t??s.
Etant donn?? que la fonction d'entr??e est une s??quence finie de r??els ou des nombres complexes , la TFD est id??al pour les informations de traitement stock??es dans les ordinateurs . En particulier, la TFD est largement utilis?? dans traitement du signal et des domaines connexes pour analyser les fr??quences contenues dans une ??chantillonn?? signaler, pour r??soudre des ??quations aux d??riv??es partielles et d'effectuer d'autres op??rations telles que circonvolutions. La DFT peut ??tre calcul?? de mani??re efficace dans la pratique en utilisant un transform??e de Fourier rapide (FFT).
Depuis algorithmes FFT sont si couramment utilis??es pour calculer la DFT, les deux termes sont souvent utilis??s indiff??remment dans des contextes familiers, bien qu'il y ait une distinction claire: "DFT" se r??f??re ?? une transformation math??matique, ind??pendamment de la fa??on dont il est calcul??, tandis que "FFT" fait r??f??rence ?? un quelconque de plusieurs algorithmes efficaces pour la TFD. Cette distinction est plus floue, cependant, par le synonyme transform??e de Fourier finie pour le DFT, qui pr??c??de apparemment le terme ??transform??e de Fourier rapide?? (Cooley et al., 1969) mais a le m??me sigle.
D??finition
La s??quence de N nombres complexes x 0, ..., x N-1 est transform?? en la s??quence de N nombres complexes X 0, ..., X N-1 par la TFD d'apr??s la formule:
o??  est un Ni??me primitive racine de l'unit??.
est un Ni??me primitive racine de l'unit??.
La transformation est parfois d??sign?? par le symbole 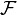 , Comme dans
, Comme dans  ou
ou 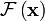 ou
ou  .
.
Le Fourier discr??te inverse (IDFT) est donn??e par
Une simple description de ces ??quations est que les nombres complexes  repr??senter l'amplitude et la phase des diff??rents composantes sinuso??dales du "signal" d'entr??e
repr??senter l'amplitude et la phase des diff??rents composantes sinuso??dales du "signal" d'entr??e 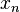 . La DFT calcule la
. La DFT calcule la  du
du 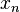 , Tandis que l'IDFT montre comment calculer le
, Tandis que l'IDFT montre comment calculer le 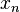 comme la somme des composantes sinuso??dales
comme la somme des composantes sinuso??dales 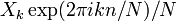 avec fr??quence
avec fr??quence  cycles par ??chantillon. En ??crivant les ??quations sous cette forme, nous faisons un usage intensif des La formule d'Euler pour exprimer en termes de sinuso??des exponentielles complexes, qui sont beaucoup plus faciles ?? manipuler. (De la m??me mani??re, par ??crit
cycles par ??chantillon. En ??crivant les ??quations sous cette forme, nous faisons un usage intensif des La formule d'Euler pour exprimer en termes de sinuso??des exponentielles complexes, qui sont beaucoup plus faciles ?? manipuler. (De la m??me mani??re, par ??crit  en forme polaire , on obtient imm??diatement l'amplitude de sinuso??de
en forme polaire , on obtient imm??diatement l'amplitude de sinuso??de 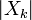 et la phase de la argumentation complexe.) Une subtilit?? importante de cette repr??sentation, aliasing, est discut??e ci-dessous.
et la phase de la argumentation complexe.) Une subtilit?? importante de cette repr??sentation, aliasing, est discut??e ci-dessous.
A noter que le facteur de normalisation et multiplier la transform??e DFT IDFT (ici 1 et 1 / N) et les signes des exposants sont simplement conventions, et diff??rent dans certains traitements. Les seules exigences de ces conventions sont que la DFT et IDFT ont des exposants de signes oppos??s et que le produit de leurs facteurs de normalisation ??tre 1 / N. Une normalisation de 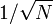 ?? la fois pour la TFD et IDFT rend les transformations unitaire, ce qui pr??sente certains avantages th??oriques, mais il est souvent plus pratique de calcul num??rique pour effectuer la mise ?? l'??chelle en une seule fois comme ci-dessus (et une mise ?? l'??chelle de l'unit?? peut ??tre pratique d'une autre mani??re).
?? la fois pour la TFD et IDFT rend les transformations unitaire, ce qui pr??sente certains avantages th??oriques, mais il est souvent plus pratique de calcul num??rique pour effectuer la mise ?? l'??chelle en une seule fois comme ci-dessus (et une mise ?? l'??chelle de l'unit?? peut ??tre pratique d'une autre mani??re).
(La convention d'un signe n??gatif dans l'exposant est souvent pratique car cela signifie que  est l'amplitude d'une "fr??quence positif"
est l'amplitude d'une "fr??quence positif" 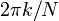 . ??quivalente, la DFT est souvent consid??r?? comme un Filtre adapt??: lors de la recherche pour une fr??quence de 1, une corr??lation du signal entrant avec une fr??quence de -1).
. ??quivalente, la DFT est souvent consid??r?? comme un Filtre adapt??: lors de la recherche pour une fr??quence de 1, une corr??lation du signal entrant avec une fr??quence de -1).
Dans la discussion qui suit les termes "s??quence" et "vecteur" seront consid??r??s comme interchangeables.
Propri??t??s
??tat complet
La transform??e de Fourier discr??te est une inversible, transformation lin??aire
avec 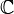 repr??sentant l'ensemble des nombres complexes . En d'autres termes, pour tout n> 0, un vecteur de dimension N a un complexe DFT et une IDFT qui sont ?? leur tour N vecteurs complexes de dimension.
repr??sentant l'ensemble des nombres complexes . En d'autres termes, pour tout n> 0, un vecteur de dimension N a un complexe DFT et une IDFT qui sont ?? leur tour N vecteurs complexes de dimension.
Orthogonalit??
Les vecteurs  pour homme base orthogonale sur l'ensemble des vecteurs complexes de N:
pour homme base orthogonale sur l'ensemble des vecteurs complexes de N:
o??  est le Kronecker. Cette condition d'orthogonalit?? peut ??tre utilis??e pour d??river la formule de l'IDFT de la d??finition de la TFD, et est ??quivalent ?? la propri??t?? unitarity ci-dessous.
est le Kronecker. Cette condition d'orthogonalit?? peut ??tre utilis??e pour d??river la formule de l'IDFT de la d??finition de la TFD, et est ??quivalent ?? la propri??t?? unitarity ci-dessous.
Le th??or??me de Plancherel et le th??or??me de Parseval
Si X et Y k k sont les TFD de x n et y n respectivement alors le Th??or??me de Plancherel ??tats:
o?? l'??toile d??signe conjugaison complexe. ??galit?? de Parseval est un cas particulier du th??or??me et les Etats Plancherel:
Ces th??or??mes sont ??galement ??quivalente ?? la condition unitaire ci-dessous.
P??riodicit??
Si l'expression qui d??finit la DFT est ??valu??e pour tous les entiers 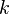 au lieu de simplement pour
au lieu de simplement pour 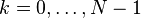 , Alors la s??quence infinie r??sultant est une extension p??riodique de la TFD, p??riodique de p??riode N.
, Alors la s??quence infinie r??sultant est une extension p??riodique de la TFD, p??riodique de p??riode N.
La p??riodicit?? peut ??tre d??montr?? directement ?? partir de la d??finition:
o?? nous avons utilis?? le fait que  . De la m??me mani??re il peut ??tre d??montr?? que la formule IDFT conduit ?? une extension p??riodique.
. De la m??me mani??re il peut ??tre d??montr?? que la formule IDFT conduit ?? une extension p??riodique.
Le th??or??me de changement de vitesse
Multipliant 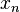 d'une phase lin??aire
d'une phase lin??aire 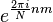 pour un certain entier
pour un certain entier 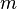 correspond ?? un d??calage circulaire de la sortie
correspond ?? un d??calage circulaire de la sortie  :
:  est remplac?? par
est remplac?? par 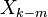 , O?? l'indice est interpr??t??e modulo
, O?? l'indice est interpr??t??e modulo  (Ce est-p??riodique). De m??me, un d??placement circulaire de l'entr??e
(Ce est-p??riodique). De m??me, un d??placement circulaire de l'entr??e 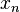 correspond ?? multiplier la sortie
correspond ?? multiplier la sortie  d'une phase lin??aire. Math??matiquement, si
d'une phase lin??aire. Math??matiquement, si 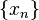 repr??sente le vecteur x puis
repr??sente le vecteur x puis
- si
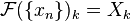
- puis
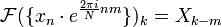
- et

Circulaire th??or??me de convolution et de corr??lation crois??e th??or??me
Le th??or??me de convolution du temps continu et discret transform??es de Fourier qui indique une convolution de deux s??quences infinite peut ??tre obtenue comme la transform??e inverse du produit des transformations individuelles. Avec les s??quences et les transform??es de longueur n, a circularit?? se pose:
La quantit?? entre parenth??ses est ??gal ?? 0 pour toutes les valeurs de 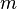 l'exception de ceux de la forme
l'exception de ceux de la forme 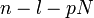 O??
O?? 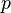 est un entier quelconque. Lors de ces valeurs, il est ??gal ?? 1. Il peut donc ??tre remplac?? par une somme infinie de Fonctions delta de Kronecker, et nous continuons en cons??quence. Notez que nous pouvons ??galement ??tendre les limites de
est un entier quelconque. Lors de ces valeurs, il est ??gal ?? 1. Il peut donc ??tre remplac?? par une somme infinie de Fonctions delta de Kronecker, et nous continuons en cons??quence. Notez que nous pouvons ??galement ??tendre les limites de 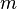 ?? l'infini, avec la compr??hension que le
?? l'infini, avec la compr??hension que le  et
et 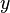 des s??quences sont d??finis comme 0 en dehors de [0, N-1]:
des s??quences sont d??finis comme 0 en dehors de [0, N-1]:
qui est la convolution de la 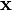 avec une s??quence p??riodiquement ??tendu
avec une s??quence p??riodiquement ??tendu 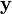 s??quence d??finie par:
s??quence d??finie par:
De m??me, il peut ??tre montr?? que:
qui est le corr??lation crois??e de 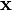 et
et 
Une ??valuation directe de la convolution ou de corr??lation sommation, ci-dessus, n??cessite 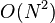 op??rations. Une m??thode indirecte, en utilisant des transformations, peut profiter de la
op??rations. Une m??thode indirecte, en utilisant des transformations, peut profiter de la 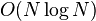 l'efficacit?? de la transform??e de Fourier rapide (FFT) afin d'obtenir de bien meilleures performances. Par ailleurs, les circonvolutions peuvent ??tre utilis??s pour calculer efficacement par TFD L'algorithme FFT et de Rader L'algorithme FFT de Bluestein.
l'efficacit?? de la transform??e de Fourier rapide (FFT) afin d'obtenir de bien meilleures performances. Par ailleurs, les circonvolutions peuvent ??tre utilis??s pour calculer efficacement par TFD L'algorithme FFT et de Rader L'algorithme FFT de Bluestein.
M??thodes ont ??galement ??t?? d??velopp??s pour utiliser convolution circulaire dans le cadre d'un processus efficace qui r??alise normale (non circulaire) convolution avec un 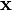 ou
ou 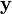 s??quence potentiellement beaucoup plus longue que la taille transformer pratique (N). Deux de ces m??thodes sont appel??es chevaucher-enregistrer et empi??tement additif.
s??quence potentiellement beaucoup plus longue que la taille transformer pratique (N). Deux de ces m??thodes sont appel??es chevaucher-enregistrer et empi??tement additif.
Trigonom??trique interpolation polynomiale
Le trigonom??trique interpolation polynomiale
 pour
pour  m??me,
m??me,  pour
pour  impair,
impair,
o?? les coefficients X k / N sont donn??es par la transform??e DFT x n ci-dessus, satisfait ?? la propri??t?? d'interpolation 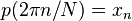 pour
pour 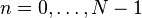 .
.
Pour encore  , Notez que la Composante de Nyquist
, Notez que la Composante de Nyquist 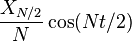 est trait??e sp??cialement.
est trait??e sp??cialement.
Cette interpolation est pas unique: aliasing implique que l'on peut ajouter ?? l'une quelconque des N fr??quences de sinuso??de complexe (par exemple, changement  ??
?? 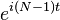 ) Sans changer la propri??t?? d'interpolation, mais donnant des valeurs diff??rentes entre le
) Sans changer la propri??t?? d'interpolation, mais donnant des valeurs diff??rentes entre le 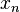 Le secteur. Le choix ci-dessus, cependant, est typique parce qu'il a deux propri??t??s utiles. Tout d'abord, il se compose de sinuso??des dont les fr??quences ont la plus petite des amplitudes possibles, et donc minimise la moyenne quadratique pente
Le secteur. Le choix ci-dessus, cependant, est typique parce qu'il a deux propri??t??s utiles. Tout d'abord, il se compose de sinuso??des dont les fr??quences ont la plus petite des amplitudes possibles, et donc minimise la moyenne quadratique pente  de la fonction d'interpolation. Deuxi??mement, si le
de la fonction d'interpolation. Deuxi??mement, si le 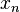 sont des nombres r??els, puis
sont des nombres r??els, puis 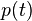 est r??el ainsi.
est r??el ainsi.
En revanche, la plus ??vidente trigonom??trique interpolation polynomiale la est celui dans lequel les fr??quences comprises entre 0 et 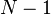 (Au lieu de plus ou moins
(Au lieu de plus ou moins 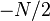 ??
??  comme ci-dessus), similaire ?? la formule DFT inverse. Cette interpolation ne minimise pas la pente, et ne est g??n??ralement valeurs r??elles pour de vrai
comme ci-dessus), similaire ?? la formule DFT inverse. Cette interpolation ne minimise pas la pente, et ne est g??n??ralement valeurs r??elles pour de vrai 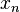 ; son utilisation est une erreur commune.
; son utilisation est une erreur commune.
Le DFT unitaire
Une autre fa??on de regarder le DFT est ?? noter que, dans la discussion ci-dessus, la DFT peut ??tre exprim??e comme une Vandermonde matrice:
o??
est une primitive Racine ni??me de l'unit??. La transform??e inverse est alors donn??e par l'inverse de la matrice ci-dessus:
Avec unitaires constantes de normalisation 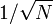 , La DFT devient transformation unitaire, d??finie par une matrice unitaire:
, La DFT devient transformation unitaire, d??finie par une matrice unitaire:
o?? det () est le facteur d??terminant fonction. Le d??terminant est le produit des valeurs propres, qui sont toujours 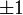 ou
ou  comme d??crit ci-dessous. Dans un espace vectoriel r??el, une transformation unitaire peut ??tre consid??r??e comme une simple rotation rigide du syst??me de coordonn??es, et toutes les propri??t??s d'une rotation rigide peut ??tre trouv??e dans la DFT unitaire.
comme d??crit ci-dessous. Dans un espace vectoriel r??el, une transformation unitaire peut ??tre consid??r??e comme une simple rotation rigide du syst??me de coordonn??es, et toutes les propri??t??s d'une rotation rigide peut ??tre trouv??e dans la DFT unitaire.
L'orthogonalit?? de la TFD est maintenant exprim?? en condition de orthonormalit?? (qui se pose dans de nombreux domaines des math??matiques comme d??crit dans racine de l'unit??):
Si 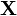 est d??fini comme la DFT du vecteur unitaire
est d??fini comme la DFT du vecteur unitaire 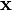 puis
puis
et le Plancherel th??or??me est exprim?? comme suit:
Si nous consid??rons la DFT comme juste une transformation qui sp??cifie simplement les composantes d'un vecteur dans un nouveau syst??me de coordonn??es de coordonn??es, le pr??c??de est juste la d??claration que le produit scalaire de deux vecteurs est conserv?? sous une transformation unitaire DFT. Pour le cas particulier  Ceci implique que la longueur d'un vecteur est conserv?? comme bien ce est juste De Parseval th??or??me:
Ceci implique que la longueur d'un vecteur est conserv?? comme bien ce est juste De Parseval th??or??me:
Exprimant le DFT inverse en termes de DFT
Une propri??t?? utile de la TFD est que la TFD inverse peut ??tre facilement exprim?? en termes de (avant) DFT, via plusieurs ??trucs?? bien connus. (Par exemple, dans les calculs, il est souvent commode de mettre en oeuvre uniquement une transform??e de Fourier rapide de transform??e correspondant ?? une direction et ensuite pour obtenir la transformation autre direction ?? partir de la premi??re).
Premi??rement, nous pouvons calculer la DFT inverse en inversant les entr??es:
(Comme d'habitude, les indices sont interpr??t??s modulo  ; Ainsi, par
; Ainsi, par 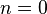 , Nous avons
, Nous avons 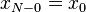 .)
.)
Deuxi??mement, on peut aussi conjuguer les entr??es et les sorties:
Troisi??mement, une variante de cette conjugaison tour, ce qui est parfois pr??f??rable car elle ne n??cessite aucune modification des valeurs de donn??es, comprend la permutation des parties r??elles et imaginaires (qui peut ??tre fait sur un ordinateur simplement en modifiant pointeurs). D??finir swap ( 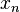 ) Comme
) Comme 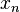 avec ses parties r??elles et imaginaires permut??es, ce est-si
avec ses parties r??elles et imaginaires permut??es, ce est-si  puis ??changer (
puis ??changer ( 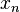 ) Est
) Est 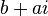 . ??quivalente, swap (
. ??quivalente, swap ( 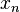 ) Est ??gal
) Est ??gal 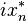 . Puis
. Puis
Autrement dit, la transformation inverse est la m??me que la transform??e directe avec les parties r??elles et imaginaires permut??es pour l'entr??e et la sortie, jusqu'?? une normalisation (Duhamel et al., 1988).
L'astuce de conjugaison peut ??galement ??tre utilis?? pour d??finir une nouvelle transformation, ??troitement li??e ?? la DFT, ce est- involutive qui est, qui est son propre inverse. En particulier,  est clairement son propre inverse:
est clairement son propre inverse:  . Une transformation involutive ??troitement apparent?? (par un facteur de (1 + i) / √2) est
. Une transformation involutive ??troitement apparent?? (par un facteur de (1 + i) / √2) est 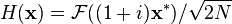 , Depuis la
, Depuis la 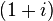 facteurs
facteurs  annuler l'2. Pour les entr??es r??elles
annuler l'2. Pour les entr??es r??elles 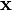 , La partie r??elle de
, La partie r??elle de  ne est autre que la transform??e de Hartley discr??te, qui est ??galement involutive.
ne est autre que la transform??e de Hartley discr??te, qui est ??galement involutive.
Valeurs et vecteurs propres
Les valeurs propres de la matrice DFT sont simples et bien connu, alors que les vecteurs propres sont compliqu??es, pas unique, et font l'objet de recherches.
Consid??rons la forme unitaire 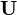 d??fini ci-dessus pour la longueur de DFT
d??fini ci-dessus pour la longueur de DFT  O??
O?? 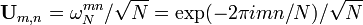 . Cette matrice v??rifie l'??quation:
. Cette matrice v??rifie l'??quation:
Ceci peut ??tre vu ?? partir des propri??t??s inverses ci-dessus: en service 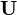 donne deux fois les donn??es originales dans l'ordre inverse, afin d'exploitation
donne deux fois les donn??es originales dans l'ordre inverse, afin d'exploitation 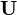 quatre fois redonne les donn??es d'origine et est ainsi le matrice identit??. Cela signifie que les valeurs propres
quatre fois redonne les donn??es d'origine et est ainsi le matrice identit??. Cela signifie que les valeurs propres 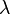 satisfaire une ??quation caract??ristique:
satisfaire une ??quation caract??ristique:
Par cons??quent, les valeurs propres de 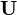 sont la quatri??me racines de l'unit??:
sont la quatri??me racines de l'unit??: 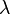 est une, -1, + i, ou - i.
est une, -1, + i, ou - i.
Depuis il ya seulement quatre valeurs propres distinctes pour ce  matrice, ils ont une certaine multiplicit?? . La multiplicit?? donne le nombre de vecteurs propres lin??airement ind??pendants correspondant ?? chaque valeur propre. (Notez qu'il existe N vecteurs propres ind??pendants; une matrice unitaire ne est jamais d??fectueux.)
matrice, ils ont une certaine multiplicit?? . La multiplicit?? donne le nombre de vecteurs propres lin??airement ind??pendants correspondant ?? chaque valeur propre. (Notez qu'il existe N vecteurs propres ind??pendants; une matrice unitaire ne est jamais d??fectueux.)
Le probl??me de leur multiplicit?? a ??t?? r??solu par McClellan et des Parcs (1972), bien qu'il ait ??t?? r??v??l?? plus tard avoir ??t?? ??quivalent ?? un probl??me r??solu par Gauss (Dickinson et Steiglitz, 1982). La multiplicit?? d??pend de la valeur de  modulo 4, et est donn?? par le tableau suivant:
modulo 4, et est donn?? par le tableau suivant:
| taille N | λ = 1 | λ = -1 | λ = - i | λ + i = |
|---|---|---|---|---|
| 4 m | m + 1 | m | m | m - 1 |
| 4 m + 1 | m + 1 | m | m | m |
| 4 m 2 + | m + 1 | m + 1 | m | m |
| 4 m + 3 | m + 1 | m + 1 | m + 1 | m |
Malheureusement, pas de formule analytique simple pour les vecteurs propres est connu. En outre, les vecteurs propres ne sont pas uniques car toute combinaison lin??aire des vecteurs propres pour la m??me valeur propre est aussi un vecteur propre pour cette valeur propre. Diff??rents chercheurs ont propos?? diff??rents choix de vecteurs propres, s??lectionn?? pour satisfaire des propri??t??s utiles comme orthogonalit?? et d'avoir des formes "simples" (par exemple, McClellan et des Parcs, 1972; Dickinson et Steiglitz, 1982; Gr??nbaum, 1982; Atakishiyev et loup, 1997;. Candan et al, 2000; Hanna et al., 2004).
Le choix des vecteurs propres de la matrice DFT a pris de l'importance ces derni??res ann??es dans le but de d??finir un analogue discret de la transform??e de Fourier-fractionn??e matrice DFT peuvent ??tre prises pour les puissances fractionnaires par exponentiation des valeurs propres (par exemple, Rubio et Santhanam, 2005). Pour le continue ?? transform??e de Fourier, les fonctions propres orthogonales naturels sont la Fonctions de Hermite, pour divers analogues discr??tes de celles-ci ont ??t?? utilis??s comme vecteurs propres de la TFD, tels que la Polyn??mes Kravchuk (Atakishiyev et Wolf, 1997). Le ??meilleur?? choix de vecteurs propres ?? d??finir une transform??e de Fourier discr??te fractionn??e reste une question ouverte, cependant.
Le DFT r??elle entr??e
Si 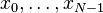 sont des nombres r??els , car elles sont souvent dans des applications pratiques, la DFT ob??it ?? la sym??trie:
sont des nombres r??els , car elles sont souvent dans des applications pratiques, la DFT ob??it ?? la sym??trie:
o?? l'??toile d??signe conjugaison complexe et les indices sont interpr??t??s modulo N.
Par cons??quent, la sortie DFT pour les entr??es r??elles est moiti?? redondante, et l'on obtient l'information compl??te en ne regardant ?? peu pr??s la moiti?? des sorties 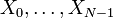 . Dans ce cas, l'??l??ment "DC"
. Dans ce cas, l'??l??ment "DC" 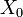 est purement r??el, et m??me pour l'??l??ment n "Nyquist"
est purement r??el, et m??me pour l'??l??ment n "Nyquist"  est aussi r??el, donc il ya exactement N non redondants nombres r??els au premier semestre + ??l??ment de Nyquist de la sortie complexe X.
est aussi r??el, donc il ya exactement N non redondants nombres r??els au premier semestre + ??l??ment de Nyquist de la sortie complexe X.
Utilisation La formule d'Euler, le polyn??me d'interpolation trigonom??trique peut alors ??tre interpr??t??e comme une somme de fonctions sinus et cosinus.
G??n??ralis?? / d??cal?? DFT
Il est possible de d??caler l'??chantillonnage transformer dans le temps et / ou dans le domaine fr??quentiel par certains changements r??els a et b, respectivement. Ce est parfois connu comme un DFT g??n??ralis??e (ou GDFT), aussi appel?? le DFT DFT d??plac?? ou offset, et poss??de des propri??t??s analogues ?? la DFT ordinaire:
Le plus souvent, d??cale de 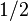 (La moiti?? d'un ??chantillon) sont utilis??s. Bien que la DFT ordinaire correspond ?? un signal p??riodique ?? la fois dans les domaines temporel et de fr??quence,
(La moiti?? d'un ??chantillon) sont utilis??s. Bien que la DFT ordinaire correspond ?? un signal p??riodique ?? la fois dans les domaines temporel et de fr??quence, 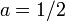 produit un signal qui est anti-p??riodique dans le domaine fr??quentiel (
produit un signal qui est anti-p??riodique dans le domaine fr??quentiel (  ) Et vice-versa pour
) Et vice-versa pour 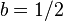 . Ainsi, le cas sp??cifique de
. Ainsi, le cas sp??cifique de 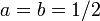 est connu comme un impair temps impair fr??quence transform??e de Fourier discr??te (ou O 2 DFT). Cette d??cal?? transformations sont le plus souvent utilis??s pour les donn??es sym??triques, pour repr??senter les diff??rentes sym??tries limites, et pour les donn??es r??elles sym??triques qu'ils correspondent aux diff??rentes formes de la discr??te et cosinus transformations sinus.
est connu comme un impair temps impair fr??quence transform??e de Fourier discr??te (ou O 2 DFT). Cette d??cal?? transformations sont le plus souvent utilis??s pour les donn??es sym??triques, pour repr??senter les diff??rentes sym??tries limites, et pour les donn??es r??elles sym??triques qu'ils correspondent aux diff??rentes formes de la discr??te et cosinus transformations sinus.
Un autre choix est int??ressant 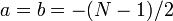 , Qui est appel?? le DFT centr??e (ou CDFT). Le DFT centr??e a la propri??t?? utile que, lorsque
, Qui est appel?? le DFT centr??e (ou CDFT). Le DFT centr??e a la propri??t?? utile que, lorsque  est un multiple de quatre, chacune de ses quatre valeurs propres (voir ci-dessus) ont multiplicit??s ??gales (Rubio et Santhanam, 2005).
est un multiple de quatre, chacune de ses quatre valeurs propres (voir ci-dessus) ont multiplicit??s ??gales (Rubio et Santhanam, 2005).
La transform??e de Fourier discr??te peut ??tre consid??r??e comme un cas particulier de la transform??e en z, ??valu??s sur le cercle unit?? dans le plan complexe; plus z transformations g??n??rales correspondent ?? des changements complexes a et b ci-dessus.
Multidimensionnelle DFT
Le DFT ordinaire calcule le transformer d'un ensemble de donn??es "unidimensionnel": une s??quence (ou array) 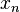 ce est une fonction d'une variable discr??te
ce est une fonction d'une variable discr??te  . Plus g??n??ralement, on peut d??finir le DFT multidimensionnelle d'un tableau multidimensionnel
. Plus g??n??ralement, on peut d??finir le DFT multidimensionnelle d'un tableau multidimensionnel 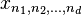 ce est une fonction de
ce est une fonction de  variables discr??tes
variables discr??tes 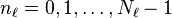 pour
pour  en
en  :
:
o?? 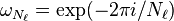 comme ci-dessus et le
comme ci-dessus et le  Les indices de production ex??cut??s ?? partir
Les indices de production ex??cut??s ?? partir 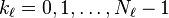 . Ceci est exprim?? dans plus compacte notation vectorielle, o?? nous d??finissons
. Ceci est exprim?? dans plus compacte notation vectorielle, o?? nous d??finissons  et
et 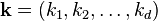 comme
comme  vecteurs de dimension des indices de 0 ??
vecteurs de dimension des indices de 0 ?? 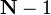 , Que nous d??finissons comme
, Que nous d??finissons comme  :
:
o?? la division 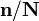 est d??fini comme ??tant
est d??fini comme ??tant 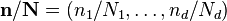 ?? effectuer ??l??ment par ??l??ment, et la somme repr??sente l'ensemble des sommations imbriqu??s ci-dessus.
?? effectuer ??l??ment par ??l??ment, et la somme repr??sente l'ensemble des sommations imbriqu??s ci-dessus.
L'inverse de la transform??e DFT multidimensionnelle est analogue au cas unidimensionnel, donn??e par:
Le multidimensionnelle DFT a une interpr??tation simple. Tout comme le DFT unidimensionnelle exprime l'entr??e 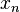 comme une superposition de sinuso??des, la DFT multidimensionnel exprime l'entr??e comme une superposition de ondes planes, ou sinuso??des oscillant long de la direction
comme une superposition de sinuso??des, la DFT multidimensionnel exprime l'entr??e comme une superposition de ondes planes, ou sinuso??des oscillant long de la direction 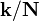 dans l'espace et ayant une amplitude
dans l'espace et ayant une amplitude  . Une telle d??composition est d'une grande importance pour tout, de traitement num??rique de l'image (d = 2) pour r??soudre des ??quations aux d??riv??es partielles en trois dimensions (d = 3) en brisant la solution dans des ondes planes.
. Une telle d??composition est d'une grande importance pour tout, de traitement num??rique de l'image (d = 2) pour r??soudre des ??quations aux d??riv??es partielles en trois dimensions (d = 3) en brisant la solution dans des ondes planes.
Calcul, la DFT multidimensionnel est simplement la composition d'une s??quence de TFD ?? une dimension le long de chaque dimension. Par exemple, dans le cas bidimensionnel  on peut d'abord calculer la
on peut d'abord calculer la 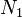 TFD ind??pendants des rang??es (par exemple, le long de
TFD ind??pendants des rang??es (par exemple, le long de  ) Pour former une nouvelle matrice
) Pour former une nouvelle matrice  , Puis calculer la
, Puis calculer la 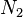 TFD ind??pendants
TFD ind??pendants 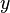 le long des colonnes (le long de
le long des colonnes (le long de 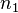 ) Pour former le r??sultat final
) Pour former le r??sultat final 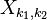 . Ou, on peut transformer les colonnes et les lignes puis-l'ordre est sans importance parce que les sommations imbriqu??s ci-dessus trajet .
. Ou, on peut transformer les colonnes et les lignes puis-l'ordre est sans importance parce que les sommations imbriqu??s ci-dessus trajet .
De ce fait, compte tenu de fa??on ?? calculer une DFT unidimensionnelle (par exemple, un algorithme FFT unidimensionnelle ordinaire), on a imm??diatement un moyen pour calculer efficacement la DFT multidimensionnel. Ceci est connu comme un algorithme ligne-colonne, mais il ya aussi intrins??quement algorithmes FFT multidimensionnels.
La v??ritable entr??e multidimensionnelle DFT
Si les entr??es 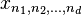 sont des nombres r??els , car elles sont souvent dans des applications pratiques, les sorties DFT pr??sentent une sym??trie conjugu?? similaire au cas unidimensionnel ci-dessus:
sont des nombres r??els , car elles sont souvent dans des applications pratiques, les sorties DFT pr??sentent une sym??trie conjugu?? similaire au cas unidimensionnel ci-dessus:
o?? l'??toile repr??sente la conjugaison complexe et le  indice -i??me est interpr??t??e modulo
indice -i??me est interpr??t??e modulo 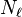 (Par
(Par 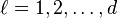 ).
).
Applications
Le DFT a vu une large utilisation dans un grand nombre de domaines; nous ne esquissons quelques exemples ci-dessous (voir aussi les r??f??rences ?? la fin). Toutes les applications de la TFD d??pendent essentiellement de la disponibilit?? d'un algorithme rapide pour calculer des transform??es de Fourier discr??te et leurs inverses, un transform??e de Fourier rapide.
L'analyse spectrale
Lorsque la TFD est utilis?? pour analyse spectrale, la  s??quence repr??sente g??n??ralement un ensemble fini de uniform??ment espac??s temps-??chantillons de quelque signal
s??quence repr??sente g??n??ralement un ensemble fini de uniform??ment espac??s temps-??chantillons de quelque signal 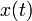 , O?? t repr??sente le temps. La conversion du temps continu aux ??chantillons (en temps discret) change le sous-jacent Transform??e de Fourier de x (t) dans un Fourier discr??te en temps de transformer (DTFT), ce qui implique g??n??ralement un type de distorsion appel?? aliasing. Choix d'une fr??quence d'??chantillonnage appropri?? (voir Fr??quence de Nyquist) est la cl?? de minimiser cette distorsion. De m??me, la conversion d'une s??quence tr??s long (ou infinie) ?? une taille implique un type de distorsion appel??e fuites, qui se manifeste comme une perte de d??tail (r??solution alias) dans le DTFT. Choix d'une longueur sous-s??quence appropri??e est la cl?? primaire de minimiser cet effet. Lorsque les donn??es disponibles (et de temps pour le traiter) est sup??rieure ?? la quantit?? n??cessaire pour atteindre la r??solution de fr??quence d??sir??e, une technique classique consiste ?? effectuer plusieurs TFD, par exemple pour cr??er une spectrogramme. Si le r??sultat souhait?? est un spectre de puissance et le bruit al??atoire ou est pr??sente dans les donn??es, la moyenne des composantes d'amplitude de la TFD multiple est un proc??d?? utile pour r??duire la variance du spectre (??galement appel??e p??riodogramme dans ce contexte); deux exemples de ces techniques sont le Proc??d?? et le Welch M??thode Bartlett.
, O?? t repr??sente le temps. La conversion du temps continu aux ??chantillons (en temps discret) change le sous-jacent Transform??e de Fourier de x (t) dans un Fourier discr??te en temps de transformer (DTFT), ce qui implique g??n??ralement un type de distorsion appel?? aliasing. Choix d'une fr??quence d'??chantillonnage appropri?? (voir Fr??quence de Nyquist) est la cl?? de minimiser cette distorsion. De m??me, la conversion d'une s??quence tr??s long (ou infinie) ?? une taille implique un type de distorsion appel??e fuites, qui se manifeste comme une perte de d??tail (r??solution alias) dans le DTFT. Choix d'une longueur sous-s??quence appropri??e est la cl?? primaire de minimiser cet effet. Lorsque les donn??es disponibles (et de temps pour le traiter) est sup??rieure ?? la quantit?? n??cessaire pour atteindre la r??solution de fr??quence d??sir??e, une technique classique consiste ?? effectuer plusieurs TFD, par exemple pour cr??er une spectrogramme. Si le r??sultat souhait?? est un spectre de puissance et le bruit al??atoire ou est pr??sente dans les donn??es, la moyenne des composantes d'amplitude de la TFD multiple est un proc??d?? utile pour r??duire la variance du spectre (??galement appel??e p??riodogramme dans ce contexte); deux exemples de ces techniques sont le Proc??d?? et le Welch M??thode Bartlett.
Une derni??re source de distorsion (ou peut-??tre illusion) est la transform??e DFT lui-m??me, parce que ce ne est qu'un ??chantillon de la DTFT discr??te, qui est une fonction d'un domaine fr??quentiel continu. Ce peut ??tre att??nu?? par l'augmentation de la r??solution de la TFD. Cette proc??dure est illustr??e dans le temps discret transform??e de Fourier article.
- La proc??dure est parfois appel??e z??ro rembourrage, qui est un mode de r??alisation particulier est utilis?? en conjonction avec le transform??e de Fourier rapide (FFT). L'inefficacit?? du effectuer des multiplications et des additions avec z??ro-??valu??e "??chantillons" est plus que compens??e par l'efficacit?? intrins??que de la FFT.
- Comme d??j?? indiqu??, les fuites impose une limite sur la r??solution inh??rente ?? la DTFT. Donc, il ya une limite pratique ?? l'avantage qui peut ??tre obtenu ?? partir d'un DFT fine.
La compression de donn??es
Le domaine du traitement de signal num??rique se appuie fortement sur les op??rations dans le domaine de fr??quence (ce est ?? dire sur la transform??e de Fourier). Par exemple, plusieurs l'image avec perte et les m??thodes de compression audio emploient transform??e de Fourier discr??te: le signal est d??coup?? en courts segments, chacun se transforme, puis les coefficients de Fourier de hautes fr??quences, qui sont suppos??s ??tre imperceptible, sont rejet??s. Le d??compresseur calcule la transform??e inverse sur la base de ce nombre r??duit de coefficients de Fourier. (Applications de compression utilisent souvent une forme sp??cialis??e de la TFD, le transform??e en cosinus discr??te ou parfois le transformer cosinus discr??te modifi??e).
??quations aux d??riv??es partielles
Transform??es de Fourier discr??tes sont souvent utilis??s pour r??soudre des ??quations aux d??riv??es partielles , o?? de nouveau la DFT est utilis??e comme une approximation pour le s??rie de Fourier (qui est r??cup??r?? dans la limite de N infinie). L'avantage de cette approche est qu'elle ??largit le signal dans exponentielles complexes e inx, qui sont propres de la diff??renciation: d dx e inx / = e dans inx. Ainsi, dans la repr??sentation de Fourier, la diff??renciation est simple-nous multiplions simplement en en. Une ??quation diff??rentielle lin??aire ?? coefficients constants est transform??e en une ??quation alg??brique facilement r??soluble. On utilise alors la TFD inverse pour transformer le r??sultat dans la repr??sentation spatiale ordinaire. Une telle approche est appel??e m??thode spectrale.
Multiplication polynomiale
Supposons que nous souhaitons pour calculer le produit polyn??me c (x) = a (x) ?? b (x). L'expression du produit ordinaire pour les coefficients de c implique un lin??aire (acyclique) convolution, o?? les indices ne ont pas "se enrouler autour." Ceci peut ??tre r????crite sous la forme d'une convolution cyclique en prenant les vecteurs de coefficients de a (x) et b (x) avec terme constant, puis l'ajout de z??ros de sorte que le coefficient r??sultant des vecteurs a et b ont la dimension d> deg (a (x) ) + deg (b (x)). Ensuite,
O?? c est le vecteur des coefficients C (x), et l'op??rateur de convolution  est d??fini de sorte
est d??fini de sorte
Mais convolution devient multiplication sous la DFT:
Voici le produit vectoriel est prise ??l??ment par ??l??ment. Ainsi, les coefficients du produit polyn??me C (X) ne sont que les termes 0, ..., deg (a (x)) + deg (b (x)) du vecteur de coefficient
Avec un Transform??e de Fourier rapide, l'algorithme r??sultant prend O (n log n) op??rations arithm??tiques. En raison de sa simplicit?? et de rapidit??, le Cooley-Tukey algorithme FFT, qui est limit??e ?? tailles composites, est souvent choisi pour l'op??ration de transformation. Dans ce cas, d doit ??tre choisi comme le plus petit entier plus grand que la somme des degr??s de polyn??mes entr??e qui est factorisable en petits facteurs premiers (par exemple de 2, 3 et 5, en fonction de l'application de la FFT).
Multiplication des grands entiers
Le plus rapide connue algorithmes pour la multiplication de tr??s grands nombres entiers utilisent la m??thode de multiplication polyn??me indiqu?? ci-dessus. Les entiers peuvent ??tre trait??es comme la valeur d'un polyn??me ??valu?? sp??cifiquement ?? la base du num??ro, avec les coefficients du polyn??me correspondant ?? des chiffres dans ladite base. Apr??s multiplication polynomiale, une ??tape de propagation de relativement faible complexit?? compl??te la multiplication.
Certains de transform??e de Fourier discr??te paires
 | 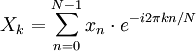 | Note |
|---|---|---|
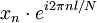 | 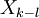 | Maj th??or??me |
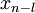 |  | |
 | 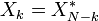 | Immobilier DFT |
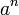 | 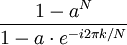 | |
 |  |
D??rivation en s??rie de Fourier
La DFT peut ??tre calcul??e comme une troncature de la s??rie de Fourier d'une suite p??riodique de impulsions.
DFT sur les champs autres que les nombres complexes
Un grand nombre des propri??t??s de la transform??e DFT ne d??pendent que du fait que 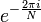 est un racine primitive de l'unit??, parfois not??e
est un racine primitive de l'unit??, parfois not??e 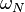 ou
ou 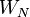 (De sorte que
(De sorte que 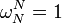 ). Ces propri??t??s comprennent l'exhaustivit??, l'orthogonalit??, Plancherel / Parseval, la p??riodicit??, d??calage, convolution, et les propri??t??s de unitarit?? ci-dessus, ainsi que de nombreux algorithmes FFT. Pour cette raison, la transform??e de Fourier discr??te peut ??tre d??fini ?? l'aide de racines de l'unit?? en d'autres domaines que les nombres complexes; Pour plus d'informations, voir transform??e de Fourier discr??te (g??n??ral).
). Ces propri??t??s comprennent l'exhaustivit??, l'orthogonalit??, Plancherel / Parseval, la p??riodicit??, d??calage, convolution, et les propri??t??s de unitarit?? ci-dessus, ainsi que de nombreux algorithmes FFT. Pour cette raison, la transform??e de Fourier discr??te peut ??tre d??fini ?? l'aide de racines de l'unit?? en d'autres domaines que les nombres complexes; Pour plus d'informations, voir transform??e de Fourier discr??te (g??n??ral).