Gottfried Wilhelm Leibniz
|
|
Des informations de cet article ou section devraient être mieux reliées aux sources mentionnées dans la bibliographie ou en liens externes. ("septembre 2009") Améliorez sa vérifiabilité en les associant par des références.
|

| Naissance | |
|---|---|
| Décès | |
| Nationalité | |
| École/tradition | |
| Principaux intérêts | |
| Idées remarquables |
Monade, continuum, principe d'identité des indiscernables, principe de raison suffisante, harmonie préétablie, compatibilisme, langage binaire, caractéristique universelle, théodicée, calcul infinitésimal |
| Œuvres principales | |
| Influencé par |
Platon, Aristote, Sénèque, Tite-Live, Augustin d'Hippone, Proclos, Scolastique (Lulle, Thomas d'Aquin, Duns Scot), Nicolas de Cues, Pic de la Mirandole, Suárez, Descartes, Grotius, Pascal, Thomasius, Hobbes, Gassendi, Huygens, Stensen, Malebranche, Bayle, Locke, philosophie chinoise |
| A influencé |
Maupertuis, Diderot, Bonnet, Kant, Frege, Bergson, Russell, Gödel, Deleuze, Serres, Kierkegaard, Adam Smith, Rousseau |
Gottfried Wilhelm Leibniz (prononcer [ˈlaɪbnɪts] ; parfois von Leibniz ; anciennement francisé en Leibnitz) (Leipzig, - Hanovre, ) est un philosophe, scientifique, mathématicien, logicien, diplomate, juriste, bibliothécaire et philologue allemand qui a écrit en latin, allemand et français.
Biographie

Fils du jurisconsulte Friedrich Leibnütz (de) (1597-1652) et de Catherina Schmuck (1621-1664), orphelin de père à 6 ans, il est suivi par son professeur de philosophie morale à l’Université de Leipzig. Celui-ci lui apprend à lire mais Leibniz, enfant précoce, affirma avoir appris par lui-même le latin. En 1663, il obtient son baccalauréat en philosophie ancienne et étudie à Iéna. Il a entre autres, comme professeur, le mathématicien et juriste Erhard Weigel (en). Plus tard, Leibniz écrira une théorie de la « jurisprudence naturelle », à savoir l'invention d'une théorie des probabilités en droit.
Il entre ensuite à l’université de droit de Leipzig. En 1666, il devient docteur en droit à Nuremberg[1], sa thèse traitant de cas juridiques embarrassants. Il refuse peu après un poste de professeur. Il s’affilie à une société alchimique, peut-être rattachée à la Rose-Croix, dont il sera secrétaire pendant deux ans. La nature exacte de son obédience est encore fort discutée par les historiens.
En 1669, il devient conseiller à la Chancellerie de l'électorat de Mayence, auprès du baron Johann Christian von Boyneburg. Leibniz réside à Mayence à l'Hôtel de Boyneburg[2]. Il prépare le projet d'une grande réforme du droit, Nova methodus discendae docendaeque jurisprudentiae. Il travaille alors sur plusieurs ouvrages concernant des thèmes politiques (Modèle de démonstrations politiques pour l’élection du roi de Pologne) ou scientifiques (Nouvelles Hypothèses physiques, 1671).
Il est envoyé en 1672 à Paris, en mission diplomatique dit-on, pour convaincre Louis XIV de porter ses conquêtes vers l’Égypte plutôt que l’Allemagne. Il y reste jusqu’en 1676 et y rencontre les grands savants de l’époque : Huygens et Malebranche, entre autres. Il se consacre aux mathématiques et laisse à Paris son manuscrit sur la quadrature arithmétique du cercle (donnant 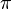 sous forme d'une série alternée). Il travaille également sur ce qui sera le calcul infinitésimal. Il conçoit en 1673 une machine à calculer qui permet d'effectuer les quatre opérations, et qui inspirera bien des machines à calculer des XIXe et XXe siècles (Arithmomètre, Curta). Avant de rejoindre Hanovre, il se rend à Londres pour étudier certains écrits d’Isaac Newton ; tous deux posent les bases du calcul intégral et différentiel. Il passe également par La Haye où il rencontre Baruch Spinoza.
sous forme d'une série alternée). Il travaille également sur ce qui sera le calcul infinitésimal. Il conçoit en 1673 une machine à calculer qui permet d'effectuer les quatre opérations, et qui inspirera bien des machines à calculer des XIXe et XXe siècles (Arithmomètre, Curta). Avant de rejoindre Hanovre, il se rend à Londres pour étudier certains écrits d’Isaac Newton ; tous deux posent les bases du calcul intégral et différentiel. Il passe également par La Haye où il rencontre Baruch Spinoza.
En 1676, à la mort de son protecteur, le baron von Boyneburg, le duc Jean-Frédéric de Brunswick-Calenberg le nomme bibliothécaire du Brunswick-Lunebourg. Il reste à ce poste au service de la maison de Hanovre pendant près de 40 ans. Il s’occupe aussi de mathématique, de physique, de religion et de diplomatie. Dans les années 1680 à 1686, il fait de nombreux voyages dans le Harz pour s'occuper de l'exploitation des mines[3]. En 1684, il publie dans les Acta Eruditorum son article sur les différentielles, et en 1686 celui sur les intégrales. En 1686, il publie en français ses Discours de métaphysique. En 1687, il se lance dans une Histoire de la maison de Brunswick, pour lequel il parcourt l’Italie en quête de documentation. En 1691, il publie à Paris, dans le Journal des savants, un Essai de dynamique où il introduit les termes énergie et action[4]. En 1700, il fonde à Berlin une académie qui ne sera inaugurée qu’en 1711. En 1710, il publie ses Essais de Théodicée, résultats de discussions avec le philosophe Pierre Bayle.
_gottfried_wilhelm_leibniz_(1646-1716),_foto_von_georg_alpers_junior,_provenance_the_estate_of_ernst_august_von_hannover,_3rd_duke_of_cumberland.jpg)
Reconnu comme le plus grand intellectuel d’Europe, et pensionné par plusieurs grandes cours (Pierre Le Grand en Russie, Charles VI en Autriche qui le fait baron), correspondant des souverains et souveraines – notamment de Sophie-Charlotte de Hanovre –, il meurt le .
Comme philosophe, il s’est intéressé fort tôt à la scolastique et à la syllogistique. Il a conçu le projet d’une encyclopédie ou « bibliothèque universelle » :
- « Il importe à la félicité du genre humain que soit fondée une Encyclopédie, c’est-à-dire une collection ordonnée de vérités suffisant, autant que faire se peut, à la déduction de toutes choses utiles. » Initia et specimina scientiae generalis, 1679-1680.
Comme mathématicien, il a fait entrer les sciences dans la nouvelle ère du calcul infinitésimal.
Philosophie
La Monadologie

Rédigée en français en 1714 et non publiée du vivant de l’auteur, la Monadologie représente une des dernières étapes de la pensée de Leibniz. En dépit de ressemblances apparentes avec des textes antérieurs, la Monadologie se distingue assez fortement d’ouvrages comme le Discours de métaphysique ou le Système nouveau de la nature et de la communication des substances. La notion de substance individuelle présente dans le Discours de métaphysique ne doit en effet pas être confondue avec celle de monade.
La force
Pour Leibniz, la physique a sa raison dans la métaphysique. Si la physique étudie les mouvements de la nature, quelle réalité est ce mouvement ? Et quelle cause a-t-il ? Le mouvement est relatif, c'est-à-dire qu'une chose se meut selon la perspective d’où nous la regardons. Le mouvement n’est donc pas la réalité elle-même ; la réalité est la force qui subsiste en dehors de tout mouvement et qui en est la cause : la force subsiste, le repos et le mouvement étant des différences phénoménales relatives.
Leibniz définit la force comme « ce qu’il y a dans l’état présent, qui porte avec soi un changement pour l’avenir. » Cette théorie entraîne un rejet de l’atomisme ; en effet, si l’atome est une réalité absolument rigide, alors il ne peut perdre de force dans les chocs. Il faut donc que ce que l’on nomme atome soit, en réalité, composé et élastique. L’idée d’atome absolu est contradictoire :
- « Les atomes ne sont que l’effet de la faiblesse de notre imagination, qui aime à se reposer et à se hâter à venir dans les sous divisions ou analyses. »
Ainsi la force est-elle la réalité : la force est substance, et toute substance est force. La force est dans un état, et cet état se modifie suivant des lois du changement. Cette succession d’états changeants possède un ordre régulier, c’est-à-dire que chaque état a une raison (cf. principe de raison suffisante) : chaque état s’explique par celui qui précède, il y trouve sa raison. À cette notion de loi se rattache également l’idée d’individualité : l’individualité est pour Leibniz une série de changements, série qui se présente comme une formule :
- « La loi du changement fait l’individualité de chaque substance particulière. »
La monade
Toute substance se développe ainsi suivant des lois intérieures, en suivant sa propre tendance : chacune a donc sa loi propre. Ainsi, si nous connaissons la nature de l’individu, pouvons-nous en dériver tous les états changeants. Cette loi de l’individualité implique des passages à des états non seulement nouveaux, mais aussi plus parfaits.
Ce qui existe est donc pour Leibniz l’individuel ; il n’existe que des unités. Ni les mouvements, ni même les corps n’ont cette substantialité : la substance étendue cartésienne suppose en effet quelque chose d’étendu, elle est seulement un composé, un agrégat qui ne possède pas par lui-même la réalité. Ainsi, sans substance absolument simple et indivisible, n’y aurait-il aucune réalité. Leibniz nomme monade cette réalité. La monade est conçue selon le modèle de notre âme :
- « l’unité substantielle demande un être accompli, indivisible et naturellement indestructible, puisque sa notion enveloppe tout ce qui lui doit arriver, ce qu’on ne saurait trouver ni dans la figure ni dans le mouvement… Mais bien dans une âme ou forme substantielle, à l’exemple de ce que l’on appelle moi. »
Nous faisons l’observation de nos états internes, et ces états (sensations, pensées, sentiments) sont en un perpétuel changement : notre âme est une monade, et c’est d’après son modèle que nous pouvons concevoir la réalité des choses, car il y a sans doute dans la nature d’autres monades qui nous sont analogues. Par la loi de l’analogie (loi qui se formule « tout comme ceci »), nous concevons toute existence comme n’étant qu’une différence de degré relativement à nous. Ainsi, par exemple, il y a des degrés inférieurs de conscience, des formes obscures de la vie psychique : il y a des monades à tous les degrés de clarté et d’obscurité. Il y a une continuité de toutes les existences, continuité qui trouve son fondement dans le principe de raison.
Dès lors, puisqu’il n’existe que des êtres doués de représentations plus ou moins claires, dont l’essence est dans cette activité représentative, la matière se trouve réduite à l’état de phénomène. La naissance et la mort sont également des phénomènes dans lesquels les monades s’obscurcissent ou s’éclaircissent. Ces phénomènes ont de la réalité dans la mesure où ils sont reliés par des lois, mais le monde, d’une manière générale, n’existe qu’en tant que représentation.
Ces monades, en se développant selon une loi interne, ne reçoivent aucune influence de l’extérieur :
- « 7. II n’y a pas moyen aussi d’expliquer comment une Monade puisse être altérée ou changée dans son intérieur par quelque autre créature, puisqu’on n’y saurait rien transposer, ni concevoir en elle aucun mouvement interne qui puisse être excité, dirigé, augmenté ou diminué là-dedans, comme cela se peut dans les composés ou il y a du changement entre les parties. Les Monades n’ont point de fenêtres par lesquelles quelque chose y puisse entrer ou sortir. » (Monadologie)
Ajoutons que le concept de monade a été influencé par la philosophie de Pierre Gassendi[5], lequel reprend la tradition atomiste incarnée par Démocrite, Épicure et Lucrèce. En effet l'atome, du grec « atomon » (indivisible) est l'élément simple dont tout est composé. La différence majeure avec la monade étant que celle-ci est d'essence spirituelle, alors que l'atome est d'essence matérielle ; et donc l'âme, qui est une monade chez Leibniz, est composée d'atomes chez Lucrèce.
L’harmonie préétablie
Dès lors, comment expliquer que tout se passe dans le monde comme si les monades s’influençaient réellement mutuellement ? Leibniz explique cette concordance par une harmonie universelle entre tous les êtres, et par un créateur commun de cette harmonie :
- « Aussi Dieu seul fait la liaison et la communication des substances, et c’est par lui que les phénomènes des uns se rencontrent et s’accordent avec ceux des autres, et par conséquent qu’il y a de la réalité dans nos perceptions. » (Discours de métaphysique)
Si les monades semblent tenir compte les unes des autres, c’est parce que Dieu les a créées pour qu’il en soit ainsi. C’est par Dieu que les monades sont créées d’un coup par fulguration, à l’état d’individualité qui les fait être comme de petits dieux. Chacune possède un point de vue singulier sur le monde, une vue de l’univers en miniature, et toutes ses perspectives ont ensemble une cohérence interne, tandis que Dieu possède l’infinité des points de vue qu’il crée sous la forme de ces substances individuelles. La force et la pensée intimes des monades sont donc une force et une pensée divines. Et l’harmonie est dès l’origine dans l’esprit de Dieu : elle est préétablie.
Si certains commentateurs (par exemple Alain Renaut, 1989) ont voulu voir dans l'harmonie préétablie un schème abstrait qui rétablit, seulement après coup, la communication entre les monades, monades qui seraient alors les signes d'une fragmentation du réel en unités indépendantes, cette interprétation a été rejetée par l'un des commentaires les plus importants de l'œuvre de Leibniz, celui de Dietrich Mahnke, intitulé La synthèse de la Mathématique universelle et de la Métaphysique de l'individu (1925). Inspirant celui de Michel Fichant, Mahnke souligne que l'harmonie universelle précède la monade : le choix de chaque monade se fait non par des volontés particulières de Dieu, mais par une volonté primitive, qui choisit l'ensemble des monades : chaque notion complète d'une monade individuée est ainsi enveloppée dans le choix primitif du monde. Aussi, « l'universalité harmonique (…) est inscrite dans la constitution interne primitive de chaque individu. »[6].
Il ressort enfin de cette idée de la monade que l’univers n’existe pas en dehors de la monade, mais qu’il est l’ensemble de toutes les perspectives. Ces perspectives naissent de Dieu. Tous les problèmes de la philosophie sont ainsi déplacés dans la théologie.
Cette transposition pose des problèmes qui ne sont pas vraiment résolus par Leibniz :
- comment une substance absolue peut-elle naître ?
- comment Dieu peut-il avoir une infinité de perspectives et en faire des substances au sein d’une harmonie préétablie ?
Malebranche résumera tous ces problèmes en une formule : Dieu ne crée pas des dieux.
L’union de l’âme et du corps
Sa théorie de l’union de l’âme et du corps suit naturellement son idée de la monade. Le corps est un agrégat de monades, dont les rapports avec l’âme sont réglés dès le départ comme deux horloges que l’on aurait synchronisées. Leibniz décrit ainsi la représentation du corps (c’est-à-dire du multiple) par l’âme :
- « Les âmes sont des unités et les corps sont des multitudes. Mais les unités, quoiqu’elles soient indivisibles, et sans partie, ne laissent de représenter des multitudes, à peu près comme toutes les lignes de la circonférence se réunissent dans le centre. »
Théodicée
Le terme de « théodicée » signifie étymologiquement « justice de Dieu » (du grec théos, Dieu, et dikè, justice). C’est un discours se proposant de « justifier la bonté de Dieu par la réfutation des arguments tirés de l’existence du mal dans ce monde, et par suite la réfutation des doctrines athées ou dualistes qui s'appuient sur ces arguments »[7]. Il est essentiel de souligner le principal enjeu de la théodicée leibnizienne. La question est d’abord : comment accorder l’existence du mal avec l’idée de la perfection générale de l’univers ? Mais, par delà les difficultés internes à la métaphysique leibnizienne, on trouve le problème suivant : comment accorder l’idée de la responsabilité ou de la culpabilité de l’homme dans le mal avec le sentiment que cet homme agit de la seule manière dont il était possible qu’il agît. La réponse de Leibniz au conflit entre nécessité et liberté est originale.
L’exemple de Judas le traître, tel qu’il est analysé dans la section 30 du Discours de Métaphysique, est éclairant : certes, il était prévisible de toute éternité que ce Judas-là dont Dieu a laissé l’essence venir à l’existence, pècherait comme il a péché, mais il n’empêche que c’est bien lui qui pèche. Le fait que cet être limité, imparfait (comme toute créature) entre dans le plan général de la création, et donc tire en un sens son existence de Dieu, ne le lave pas en lui-même de son imperfection. C’est bien lui qui est imparfait, de même que la roue dentée, dans une montre, n’est rien d’autre qu’une roue dentée : le fait que l’horloger l’utilise pour fabriquer une montre ne rend pas cet horloger responsable du fait que cette roue dentée n’est rien d’autre, rien de mieux qu’une roue dentée.
Le principe de raison suffisante, parfois nommé principe de « la raison déterminante » ou le « grand principe du pourquoi », est le principe fondamental qui a guidé Leibniz dans ses recherches : rien n’est sans une raison qui explique pourquoi il est, plutôt qu’il n’est pas, et pourquoi il est ainsi, plutôt qu’autrement. Leibniz ne nie pas que le mal existe. Il affirme toutefois que tous les maux ne peuvent pas être moindres : ces maux trouvent leur explication et leur justification dans l’ensemble, dans l’harmonie du tableau de l’univers. « Les défauts apparents du monde entier, ces taches d’un soleil dont le nôtre n’est qu’un rayon, relèvent sa beauté bien loin de la diminuer ». (Théodicée, 1710 - parution en 1747).
Répondant à Bayle, il établit la démonstration suivante : si Dieu existe, il est parfait et unique. Or, si Dieu est parfait, il est « nécessairement » tout-puissant, toute bonté et toute justice, toute sagesse. Ainsi, si Dieu existe, il a, par nécessité, pu, voulu et su créer le moins imparfait de tous les mondes imparfaits ; le monde le mieux adapté aux fins suprêmes.
En 1759, dans le conte philosophique Candide, Voltaire fait de son personnage Pangloss le porte-parole du providentialisme de Leibniz. Il y déforme volontairement sa doctrine en la réduisant à la formule : « tout est au mieux dans le meilleur des mondes possibles ». Cette formule ne se trouve pas dans l’œuvre leibnizienne. Jean-Jacques Rousseau rappellera à Voltaire l’aspect contraignant de la démonstration de Leibniz : « Ces questions se rapportent toutes à l’existence de Dieu. (…) Si l’on m’accorde la première proposition, jamais on n’ébranlera les suivantes ; si on la nie, il ne faut pas discuter sur ses conséquences. » (Lettre du )[réf. nécessaire]
Toutefois, le texte de Voltaire ne s'oppose pas à Leibniz sur un plan théologique ni métaphysique : le conte de Candide trouve son origine dans l'opposition entre Voltaire et Rousseau, et son contenu cherche à montrer que ce ne sont pas les raisonnements des métaphysiciens qui mettront fin à nos maux, faisant l'apologie d'une philosophie volontariste invitant les hommes à organiser eux-mêmes la vie terrestre et où le travail est présenté comme source de progrès matériels et moraux qui rendront les hommes plus heureux[8].
Nouveaux essais sur l’entendement humain
Les Nouveaux essais sur l'entendement humain, rédigés en français, sont la réponse de Leibniz à l’Essai sur l’entendement humain de John Locke. Le philosophe anglais défend une position empiriste, selon laquelle toutes nos idées nous viennent de l’expérience. Leibniz, sous la forme d’un dialogue imaginaire entre Philalèthe, qui cite les passages du livre de Locke, et Théophile, qui lui oppose les arguments leibniziens, défend une position innéiste : certaines idées sont en notre esprit dès la naissance. Ce sont des idées qui sont constitutives de notre entendement même, comme celle de causalité. Les idées innées peuvent être activées par l'expérience, mais il a fallu pour cela qu’elles existent d’abord potentiellement dans notre entendement.
Les Nouveaux essais sont achevés en 1705. Mais, la mort de Locke convainc Leibniz de reporter leur publication. Ils ne paraîtront finalement qu’en 1765.
Histoire
Leibniz, dès les années 1670, a aussi une importante activité d'historien[9]. Elle est au début liée à son intérêt pour le droit, qui le conduit à développer des travaux d'histoire du droit, et à publier, dans les années 1690, un important recueil de documents juridiques médiévaux. Elle est aussi liée à la commande que lui passe en 1685 l'électeur de Hanovre : une histoire de la maison de Brunswick. Convaincu que cette famille aristocratique a en partie des origines semblables à la maison italienne des Este, Leibniz entreprend d'importants travaux sur l'histoire de l'Europe du IXe au XIe siècle. Leibniz se rend alors en Italie, de 1687 à 1690, pour réunir la documentation nécessaire à son enquête. Leibniz participe ainsi aux travaux de l'époque, qui fondent, avec Jean Mabillon, Étienne Baluze ou Papebrocke, la critique historique ; il apporte des éléments importants aux questions de chronologie et de généalogie des familles souveraines d'Europe. Son travail ne sera pas achevé à son décès en 1716. Il engage au sujet de la maison des Este une polémique fameuse avec le grand savant italien Antonio Muratori.
Mathématiques
Les travaux mathématiques de Leibniz se trouvent dans le Journal des savants de Paris, les Acta Eruditorum de Leipzig (qu’il a contribué à fonder) ainsi que dans son abondante correspondance avec Huygens, les frères Bernoulli, l’Hôpital, Varignon, etc.
Le « nouveau calcul »
L’algorithme différentio-intégral achève une recherche débutée avec la codification de l’algèbre par Viète et l’algébrisation de la géométrie par Descartes. Tout le XVIIe siècle étudie l’indivisible et l’infiniment petit. Comme Newton, Leibniz domine tôt les indéterminations dans le calcul des dérivées. De plus il développe un algorithme qui est l’outil majeur pour l’analyse d’un tout et de ses parties, fondé sur l’idée que toute chose intègre des petits éléments dont les variations concourent à l’unité. Ses travaux sur ce qu’il appelait la « spécieuse supérieure » seront poursuivis par les frères Bernoulli, le marquis de l’Hospital, Euler et Lagrange.
Notation de Leibniz
Leibniz développe une symbolique mathématique qu’il tente d’intégrer dans une notion plus générale qu’il appelle sa caractéristique universelle, et qu’il voulait pouvoir appliquer à tous les domaines.
Il est à l’origine du terme de « fonction » (1692, de functio : exécution), de celui de « coordonnées », de la notation du produit de a par b sous la forme a.b ou ab, d’une définition logique de l’égalité, du terme de « différentielle » (qu’Isaac Newton appelle « fluxion »), de la notation différentielle 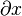 , du symbole
, du symbole 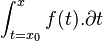 pour l’intégrale. Leibniz popularise l'utilisation de : (deux-points) pour représenter la division. Mis à part les mathématiciens anglophones, ce symbole est adopté dès 1684 par une bonne partie de l'Europe[10].
pour l’intégrale. Leibniz popularise l'utilisation de : (deux-points) pour représenter la division. Mis à part les mathématiciens anglophones, ce symbole est adopté dès 1684 par une bonne partie de l'Europe[10].
Calcul infinitésimal : Newton ou Leibniz ?
Dans l’histoire du calcul infinitésimal, le procès de Newton contre Leibniz est resté célèbre. Newton et Leibniz avaient trouvé l’art de lever les indéterminations dans le calcul des tangentes ou dérivées. Mais Newton a publié tard (son procès intervient en 1713, presque 30 ans après les publications de Leibniz : 1684 et 1686) et, surtout, Newton n’a ni l’algorithme différentio-intégral fondé sur l’idée que les choses sont constituées de petits éléments, ni l’approche arithmétique nécessaire à des différentielles conçues comme « petites différences finies ».
Autres travaux

Leibniz s’intéresse aux systèmes d’équations et pressent l’usage des déterminants. Dans son traité sur l’art combinatoire, science générale de la forme et des formules, il développe des techniques de substitution pour la résolution d’équation. Il travaille sur la convergence des séries, le développement en série entière des fonctions comme l’exponentielle, le logarithme, les fonctions trigonométriques (1673). Il découvre la courbe brachistochrone et s’intéresse à la rectification des courbes (calcul de leur longueur). Il a étudié le traité des coniques de Pascal et écrit sur le sujet. Il est le premier à créer la fonction 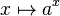 (conspectus calculi). Il étudie les enveloppes de courbes et la recherche d’extremum pour une fonction (Nova methodus pro maximis et minimis 1684). Il conçoit une machine arithmétique inspirée de la Pascaline. Il tente aussi une incursion dans la théorie des graphes et la topologie (analysis situs).
(conspectus calculi). Il étudie les enveloppes de courbes et la recherche d’extremum pour une fonction (Nova methodus pro maximis et minimis 1684). Il conçoit une machine arithmétique inspirée de la Pascaline. Il tente aussi une incursion dans la théorie des graphes et la topologie (analysis situs).
On trouve dans le Compte Rendu de l’Académie des Sciences (Paris, 1703, p. 85-89 des Mémoires[11]) un article de Leibniz intitulé Explication de l’arithmétique binaire, qui se sert des seuls caractères 0 & 1, (…). Reconnaissant cette manière de représenter les nombres comme étant un héritage très lointain du fondateur de l’Empire Chinois « Fohy », Leibniz s’interroge longuement sur l’utilité des concepts qu’il vient de présenter, notamment en ce qui concerne les règles arithmétiques qu’il développe. Finalement, il semble conclure que la seule utilité qu’il voit dans tout ceci est une sorte de beauté essentielle, qui révèle la nature intrinsèque des nombres et de leurs liens mutuels.
Physique
Leibniz, comme de nombreux mathématiciens de son temps, était aussi physicien. Il a très tôt été mécaniste et l'est resté toute sa vie, mais une différence profonde le sépare d'Isaac Newton : si Newton considère que « la physique se garde de la métaphysique » et cherche à prévoir les phénomènes par sa physique, Leibniz cherche à découvrir l'essence cachée des choses et du monde, sans réussir (ni vouloir ?) à obtenir des calculs précis à propos de phénomènes quelconques. D'ailleurs jamais il n'employa son calcul infinitésimal pour expliquer les lois de la nature. Il en est venu ainsi à reprocher à René Descartes et à Newton de ne pas savoir se passer d'un Deus ex machina (une raison divine cachée) dans leurs physiques, car celles-ci n'expliquaient pas tout ce qui est, ce qui est possible et ce qui n'est pas[12].
| Concept | Apports de Leibniz |
|---|---|
| Énergie cinétique (1/2)mv2 | Invention du concept, sous le nom de « force vive ». Il s'oppose à une idée de Descartes qui était que la quantité mv (qu'on appelait à cette époque force motrice ou quantité de mouvement) se conservait dans les chocs, indépendamment des directions du mouvement[13]. Leibniz écrivit « Il se trouve par la raison et par l’expérience que c’est la force vive absolue [mv2] qui se conserve et nullement la quantité de mouvement » (Essai de dynamique, 1691). |
| Principe de moindre action | Le principe de la moindre action a été découvert en 1740 par Maupertuis. En 1751, Samuel König affirma avoir une lettre de Leibniz, datée de 1707, dans laquelle il énonçait ce même principe, donc bien avant Maupertuis. L'Académie de Berlin chargea Leonhard Euler de se pencher sur le problème de l'authenticité de cette lettre. Euler fit un rapport, en 1752, où il conclut à un faux[14] : König aurait inventé l'existence de cette lettre de Leibniz. Ce qui n'empêche pas Leibniz d'avoir, en optique, avancé un énoncé (sans formalisme mathématique) proche du principe de Fermat[15], vers 1682[n 1]. |
| Définitions de l’espace et du temps | Leibniz s'opposa à Isaac Newton au sujet de l'espace absolu que définit ce dernier. « J’ai marqué plus d’une fois que je tenais l’espace pour quelque chose de purement relatif, comme le temps ; pour un ordre de coexistences comme le temps est un ordre de successions… Je ne crois pas qu’il y ait aucun espace sans matière. Les expériences qu’on appelle du vide, n’excluent qu’une matière grossière[18]. » |
Logique
« La Logique est pour Leibniz la Clef de la Nature[n 2] »
La logique que développa Leibniz fut sans doute une des plus importantes depuis l’invention de la syllogistique aristotélicienne.
Leibniz estime qu'Aristote est le « premier qui ait écrit mathématiquement en dehors des mathématiques[20],[21] ». Il avait une grande admiration pour son œuvre[22]. Cependant, il l'estimait imparfaite[23]. Il trouvait que la logique aristotélicienne présentait des lacunes[24] et souhaitait l'ameliorer[25]. Il s'intéressa particulièrement à la syllogistique et ses premières contributions dans ce domaine se trouvent dans le De arte combinatoria[24].
Les deux grandes caractéristiques de la logique de Leibniz consistent d’une part dans le fait qu’il a voulu constituer un langage universel (la lingua caracteristica universalis) prenant en compte non seulement les connaissances mathématiques, mais aussi la jurisprudence (il établit les correspondances à la base de la déontique), l’ontologie (Leibniz critiqua la définition que René Descartes donnait de la substance), voire la musique.
À côté de cette langue universelle, Leibniz a rêvé d’une logique qui serait calcul algorithmique et donc mécaniquement décidable[réf. nécessaire] (calculus ratiocinator). Leibniz annonce ainsi la langue artificielle et purement formelle développée par Frege.[réf. nécessaire]
Il a en même temps eu conscience des limites de la logique formelle en affirmant que toute modélisation, pour être correcte, nécessite d'être faite strictement en analogie avec le phénomène modélisé.[réf. nécessaire]
Leibniz est le logicien le plus important entre Aristote et les logiciens du XIXe siècle George Boole et Augustus De Morgan tous deux auteurs de livres qui sont à l'origine de la logique formelle moderne.[réf. nécessaire] Les principes fondamentaux de la logique de Leibniz peuvent être résumés en ces deux concepts :
- Toutes nos idées sont formées d'un très petit nombre d'idées simples qui forment l'alphabet de la pensée humaine.
- Les idées dites complexes procèdent de ces idées simples par un système de composition syntaxique comparable aux règles de calcul de l'arithmétique et de l'algèbre.
Leibniz n'a rien publié de son vivant sur la logique formelle; la plupart de ses textes consistent en des esquisses.
Jeu d’échecs
Leibniz était un excellent joueur d’échecs ; il s'est notamment intéressé à l'aspect scientifique et logique du jeu (par opposition aux jeux qui comportent une part de hasard), et fut le premier à considérer celui-ci comme une science[26].
Bibliographie
- Notices d’autorité : Fichier d’autorité international virtuel • International Standard Name Identifier • Union List of Artist Names • Bibliothèque nationale de France • Système universitaire de documentation • Bibliothèque du Congrès • Gemeinsame Normdatei • Institut central pour le registre unique • Bibliothèque nationale de la Diète • Bibliothèque nationale d'Espagne • WorldCat
Éditions des œuvres de Leibniz
- Die Mathematische Schriften, éd. C. I. Gerhardt, Berlin, 1850-1853, réimpr. Georg Olms Verlag, 1962. Sur Archive : tome 1, tome 2, tome 3,tome 4, tome 5, tome 6, tome 7.
- Die Philosophischen Schriften, éd. C. I. Gerhardt, Berlin, 1875-1890, réimpr. Georg Olms Verlag, 1978. Sur Archive : tome 1, tome 2,tome 3, tome 4, tome 5, tome 6, tome 7.
- Opuscules et fragments inédits, extraits des manuscrits de la bibliothèque de Hanovre, éd. par L. Couturat, 1903, réimpr. Georg Olms Verlag, 1988.
- Sämtliche Schriften und Briefe, éd. Deutsche Akamedie der Wissenschaften, Berlin, 1923 ss.
Œuvres de Leibniz
L’œuvre de Leibniz a été écrite en latin (40%), en français (35%) et en allemand (25%).
- Disputatio meptaphysics de principio individui (Disputation métaphysique sur le principe d'individuation) (1663, traduite en français par Jeannine Quillet, Les Études philosophiques, 1979, 1, p. 79-105)
- De arte combinatoria (1666)
- Disputatio de casibus perplexis injure (1667)
- Nova methodus discendae docendaeque jurisprudentiae (1667)
- Ratio corporis iuris reconcinnandi (1668)
- Confessio naturæ contra atheistas (1668)
- Defensio Trinitatis per nova Reperta Logica (1669)
- Théorie du mouvement concret et du mouvement abstrait (1670)
- Hypothesis Physica Nova (1671)
- Confessio philosophi (1673)
- Quadrature arithmétique du cercle, de l’ellipse et de l’hyperbole (vers 1674)
- Specimen calculi universalis (1678-1684)
- Calcul différentiel: Nouvelle méthode pour les maxima et minima, ainsi que les tangentes, qui ne bute ni sur les fractions ni sur les irrationnelles, avec un mode original de calcul (en latin, Acta Eruditorum, 1684)
- Nova Methodus pro maximis et minimis (1684)
- Meditationes de cognitione, veritate et ideis (1684)[27]
- Generales inquisitiones de analysis notionum et veritatum (1686)
- Brevis demonstratio erroris memorabilis Cartesii (1686)
- Discours de métaphysique (1686)
- Correspondance avec Arnauld
- Intégrales: De la géométrie supérieure et analyse des indivisibles comme des infinis (en latin, Acta Eruditorum, 1686)
- Discours touchant la méthode de la certitude et l’art d’inventer pour finir les disputes et faire en peu de temps de grands progrès (1688-1690)
- Primae veritates (1689)
- Dynamica de potentia et legibus naturae corporeae (1689)
- Essai de dynamique (Journal des Savants, 1691)
- Animadversiones ad Cartesii principia philosophiae (1691)
- Protogaea, écrit entre 1690 et 1693 mais publié seulement après sa mort, connu en France sous le nom de Protogée, ou de la formation et des Révolutions du globe
- Système nouveau de la nature et de la communication des substances (1695)
- Matheis rationis (environ 1700)
- Nouveaux essais sur L’entendement humain (1705)
- Explication de l'Arithmétique Binaire (1705)
- Essais de théodicée (1710)
- Monadologie (1714)
- Principes de la nature et de la grâce fondés en raison (1714)
Traductions en français d’œuvres mathématiques:
- Leibniz (trad. Marc Parmentier, Eberhard Knobloch), Quadrature arithmétique du cercle, de l’ellipse et de l’hyperbole et la trigonométrie sans tables trigonométriques qui en est le corollaire, Vrin, , 369 p. (ISBN 2-7116-1635-5, lire en ligne)
- L’estime des apparences. 21 manuscrits de Leibniz sur les probabilités, la théorie des jeux, l’espérance de vie ; texte établi, trad., introd. et annoté par Marc Parmentier. Paris : J. Vrin, 1995. (Mathesis). (ISBN 2-7116-1229-5).
- La caractéristique géométrique ; texte établi et annoté par Javier Echeverría ; traduit, annoté par Marc Parmentier. Paris : J. Vrin, 1995. (Mathesis). (ISBN 2-7116-1228-7).
- Leibniz (trad. Marc Parmentier, préf. Marc Parmentier), La naissance du calcul différentiel, Vrin, , 504 p. (ISBN 2-7116-0997-9, lire en ligne) Réunion de 26 articles parus dans « Acta eruditorum ». - Texte en français seul, traduction du latin.
Études sur Leibniz
- Yvon Belaval, Leibniz : Initiation à sa philosophie, Vrin, coll. « Bibliothèque d'histoire de la philosophie », (présentation en ligne)
- Yvon Belaval, Leibniz, critique de Descartes, Gallimard, « Tel », 1960.
- Yvon Belaval, Études leibniziennes, de Leibniz à Hegel, Gallimard, « Tel », 1993.
- Fernand Brunner, Études sur la signification historique de la philosophie de Leibniz, Vrin, Paris, 1950.
- (la) Israel Gottlieb Canz, Philosophiae Leibnitianae et Wolfianae usus in Theologia (1728).
- Louis Couturat, La logique de Leibniz, Georg Olms Verlag, (présentation en ligne)
- Gilles Deleuze, Le Pli – Leibniz et le baroque, Les éditions de Minuit (coll. « Critique »), Paris, 1988, 191 p.
- Claire Fauvergue, Diderot, lecteur et interprète de Leibniz, Honoré Champion, 2006.
- Michel Fichant, L’invention métaphysique (introduction à l’édition Folio de la Monadologie), Folio, 2004.
- Martial Gueroult, Leibniz, Dynamique et métaphysique, rééd. Aubier, 1967.
- Herbert H. Knecht, La Logique chez Leibniz : essais sur le rationalisme baroque, L'Âge d'Homme, coll. « Dialectica », (présentation en ligne)
- Mogens Laerke, Leibniz lecteur de Spinoza. La genèse d'une opposition complexe, Paris, Honoré Champion, coll. "Travaux de philosophie", 2008.
- Massimo Mugnai, Leibniz, le penseur de l’universel, Les génies de la science, août 2006 no 28.
- Jean-Baptiste Rauzy, La doctrine leibnizienne de la verité. Aspects logiques et ontologiques, Paris, Vrin, 2001.
- Bertrand Russell, La philosophie de Leibniz, (1900) Éditions des archives contemporaines - EAC, 2000).
- Michel Serfati, La révolution symbolique : La constitution de l'écriture mathématique, Paris, Éditions Pétra, 2005.
- Michel Serres, Le système de Leibniz et ses modèles mathématiques, Paris, PUF, 1968; rééd. en 1 volume.
- Gabriel Tarde, Monadologie et sociologie, 1893, Les empêcheurs de penser en rond, 1999.
Notes et références
Notes
- ↑ 1er volume d'Acta Eruditorum[16] :
« la cause finale suffit pour deviner quelles lois la lumière suit, car si on fait l’hypothèse que la nature a eu pour but de conduire les rayons lumineux d’un point à un autre par le chemin le plus facile, on trouve admirablement bien toutes ces lois. »
— Leibniz[17]
- ↑ neque enim aliud est Naturae quam Ars quaedam Magna. (Appendice du De Complexionibus)[19].
Références
- ↑ Plus précisément, à l'Université Altdorf (ou Altdorfina, ou encore Academia Norica) à Altdorf bei Nürnberg.
- ↑ Gottfried Wilhelm Leibniz, Jacob Thomasius, Richard Bodéüs, Correspondance, 1663-1672, Vrin, 1993, (ISBN 978-2-7116-1145-4), p. 53 [lire en ligne].
- ↑ Leibniz a consacré l'équivalent de trois années au métier d'ingénieur des mines. Il s'occupa principalement de mettre au point des dispositifs d'extraction des eaux des mines grâce à des moulins à vent. Il entra en conflit avec les exploitants qui n'acceptaient pas ses nouvelles idées. Cela le conduisit à se poser des questions sur l'origine des fossiles, qu'il attribuait initialement à l'effet du hasard, mais dont il reconnut plus tard l'origine vivante. Son livre Protogaea ne sera publié qu'après sa mort, car les théories qu'il y développe sur l'histoire de la terre pouvaient déplaire aux autorités religieuses.
- ↑ André Robinet, Architectonique disjonctive, automates systémiques et idéalité transcendantale dans l'œuvre de G. W. Leibniz, Vrin, 1986, (ISBN 978-2-7116-0914-7), p. 79 [lire en ligne].
- ↑ Michel Fichant, « La réception de Gassendi dans l’œuvre de la maturité de Leibniz », dans Gassendi et l’Europe Vrin, Paris, 1996 .
- ↑ Michel Fichant, Science et métaphysique chez Descartes et Leibniz, PUF, 1998, chap. V, p. 134.
- ↑ Mot Théodicée dans Vocabulaire technique et critique de la philosophie par André Lalande, éditions PUF, 1980, (ISBN 2-13-036474-8).
- ↑ Lagarde et Michard, tome XVIIIe siècle, chapitre Voltaire, § Voltaire et la Providence et § Candide.
- ↑ Quelques ouvrages importants : Louis Davillé, Leibniz historien. Essai sur l’activité et la méthode historique de Leibniz, Paris, Alcan, 1909, et « Le développement de la méthode historique de Leibniz », Revue de Synthèse historique, XXIII, 3, 1911, p. 257-268, XXIV, 1, p. 1-31 ; Werner Conze, Leibniz als Historiker, Berlin, de Gruyter, 1951 ; Gunther Scheel, « Leibniz als Historiker des Welfenhauses », in Wilhelm Totok et Carl Haase (eds.), Leibniz. Sein Leben, sein Wirken, sein Welt, Hanovre, Verl. für Literatur und Zeitgeschehen, 1966, p. 227-276, et « Leibniz historien », in Georges Bastide (éd.), Leibniz. Aspects de l’homme et de l’œuvre. Journées Leibniz, organisées par le Centre national de Synthèse, les 28, 29 et 30 mai 1966, Paris, Aubier Montaigne, 1968, p. 45-60.
- ↑ (en) William P. Berlinghoff et Fernando Q. Gouvêa, Math Through the Ages : A Gentle History for Teachers and Others, MAA, coll. « Classroom ressource materials » (1re éd. 2004), 273 p. (ISBN 9780883857366, lire en ligne), « Readind And Writing Arithmetic Where the Symbols Came From », p. 76.
- ↑ disponible sur Gallica
- ↑ « Histoire de la philosophie » par Émile Bréhier, Tomes I à III, Éditeur PUF, 1931, réédité en 1994 (7e édition), (ISBN 213-044378-8). Tome II, chapitre VIII Leibniz, §V Mécanisme et dynamisme.
- ↑ Michel Blay et Robert Halleux, La Science classique, XVIe-XVIIIe siècle : Dictionnaire critique, Flammarion, (ISBN 2-08-2115666), p. 528-529
- ↑ Histoire du principe de moindre action par F Martin-Robine, 2006, Vuibert, p. 97-98.
- ↑ Michel Blay et Robert Halleux, La Science classique, XVIe-XVIIIe siècle : Dictionnaire critique, Flammarion, (ISBN 2-08-2115666), p. 338
- ↑ Jean-Jacques Samueli, « Euler en défense de Maupertuis à propos du principe de moindre action », sur Bibnum, (consulté le 22 mars 2015), p. 7-8.
- ↑ Voir aussi Pensées sur la religion et la morale, la Ve Nyon, (lire en ligne), « Considérations des Causes finales, propres à faire connaître et prouver l'Existence de Dieu », p. 85 ; Pensées de Leibnitz sur la religion et la morale disponible sur Gallica
- ↑ Troisième écrit de M. Leibniz ou réponse à seconde réplique de M. Clarke, 27 février 1716, trad. L. Prenant. Voir aussi l'extrait de la Troisième lettre de Leibniz à Clarke du 25 février 1716 dans l'article Principe de relativité.
- ↑ Yvon Belaval 2005, p. 57
- ↑ François TRÉMOLIÈRE, « Organon, Aristote : 2. Langage et penser : la naissance de la logique », sur Encyclopædia universalis (consulté le 29 mars 2015)
- ↑ Jacques Bouveresse, « Descartes, le « bon sens », la logique et les vérités éternelles », dans ESSAI V - DESCARTES, LEIBNIZ, KANT, Marseille, Agone, (lire en ligne), Tradition et innovation : Leibniz et ses prédécesseurs.
- ↑ Herbert H. Knecht 1981, p. 37
- ↑ Louis Couturat 1961, p. 2
- 1 2 Herbert H. Knecht 1981, p. 38-39
- ↑ Robert Blanché, « Logique : 4. L'ère de la logique dite « classique » », sur Encyclopædia universalis (consulté le 11 mars 2015) : « Il accepte ce qui a été fait, il le reprend, mais pour l'approfondir. La logique traditionnelle n'est qu'un échantillon d'une logique générale, qui reste à établir. »
- ↑ http://www.mjae.com/roos-memoriam.html
- ↑ (de) « Leibniz’ Abhandlung ‘Meditationes de cognitione, veritate et ideis` von 1684 – eine Diskussion mit Blick auf den ‘Tractus de intellectus emendatione’ des Baruch Spinoza » [PDF], sur www.uni-muenster.de, Thomas Kisser, (consulté le 11 novembre 2014)
Voir aussi
Articles connexes
En philosophie
- Métaphysique
- Descartes
- Caractéristique de Leibniz
- Compossibilité
- Monadologie
- Principe de raison suffisante
- Spinoza
- Aufklärung
- mathesis universalis
En mathématiques
- Analyse des infiniment petits pour l'intelligence des lignes courbes, premier ouvrage en français traitant du calcul différentiel de Leibniz.
- Formules de Leibniz : pour la dérivée nième d’un produit, pour le calcul de
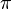 , pour le calcul du déterminant
, pour le calcul du déterminant - Fonction vectorielle et fonction scalaire de Leibniz dans les barycentres ainsi que le théorème de Leibniz dans ce même domaine
- Isochrone de Leibniz
- Critère de Leibniz pour la convergence d’une série alternée
- Mathématiques en Europe au XVIIe siècle
Communauté scientifique Leibniz, WGL
- Réseau allemand d'instituts de recherches scientifiques (Leibniz-Gemeinschaft)
Autres
- Les célèbres biscuits allemands « Choco Leibniz » et le Petit beurre allemand « Leibniz-Keks (en) », fabriqués depuis 1891, ont été nommés en l’honneur du philosophe de Hanovre par la biscuiterie Bahlsen, fondée dans cette même ville.
Liens externes
- Ouvrages de Leibniz numérisés par le SCD de l’Université de Strasbourg
- Texte de Leibniz sur la chaînette, en ligne et commenté sur le site BibNum
- Texte de Leibniz sur sa machine à calculer, en ligne et commenté sur le site BibNum.
- Manuscrit de Leibniz sur la numération binaire, en ligne et commenté sur le site BibNum.
- Cours de Gilles Deleuze sur Leibniz
- La Monadologie
- La Monadologie (audiolivre)

- La Monadologie : textes avec concordances et liste de fréquence
- Leibniz et Pascal : l’histoire d’une relation féconde entre deux mathématiciens philosophes
- Explication de l’arithmétique binaire, par Leibniz, sur le site web de Laurent Bloch.
- Série de 12 cours donnés par Jacques Bouveresse au Collège de France début 2009 : « Dans le labyrinthe : nécessité, contingence et liberté chez Leibniz ». également disponible en podcast :
- Portail de la philosophie
- Portail de la logique
- Portail des mathématiques
- Portail de la physique
- Portail du XVIIe siècle
- Portail de l’Allemagne