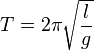Christian Huygens

Pour les articles homonymes, voir Huygens.

Christian Huygens

Christian Huygens

Données clés

Naissance	14 avril 1629 La Haye (Provinces-Unies)
Décès	8 juillet 1695 (à 66 ans) La Haye (Provinces-Unies)
Nationalité	Néerlandais
Champs	Mathématiques, physique, astronomie
Institutions	Académie des sciences Royal Society
Diplôme	Université de Leyde
Renommé pour	Principe de Huygens-Fresnel Biréfringence Théorie des ondes Force centrifuge Titan

Christian Huygens

Christian Huygens, ou Christian Huyghens (^{Prononciation}), tel qu'il est connu dans les lettres françaises depuis le Grand Siècle (en néerlandais Christianus Huygens, en latin Christianus Hugenius, en néerlandais moderne Christiaan Huygens, né le 14 avril 1629 à La Haye et mort le 8 juillet 1695 dans la même ville, est un mathématicien, un astronome et un physicien néerlandais. Il est le fils de Constantin Huygens.

Biographie

Huygens est généralement crédité pour son rôle fondamental dans le développement du calcul moderne, en particulier pour avoir développé les techniques de sommation et d'intégration nécessaires à la découverte de l'isochronisme de la cycloïde. En sciences physiques il est célèbre pour la formulation de la théorie ondulatoire de la lumière^[1], et le calcul de la force centrifuge. Il s'est opposé à Leibniz, à la fin de sa vie, dans la mesure où il lui a semblé que le calcul infinitésimal n'était au fond qu'une affaire de langage, la géométrie devant seule intervenir dans la mise en forme mathématique des phénomènes. Le calcul ne serait en quelque sorte que l'automatisation de procédures de démonstrations qu'un géomètre avisé sait produire par d'autres moyens^{[réf. souhaitée]}. Le développement du calcul infinitésimal à la fin de sa vie lui montrera tout de même, comme le révèle sa correspondance avec Leibniz et l'Hospital, la puissance de cet outil.

Jeune, Huygens eut pour précepteur le mathématicien Jan Stampioen, qu'il partagea à peu d'intervalle avec Guillaume II d'Orange-Nassau ; puis Frans Van Schooten, qui l'initia à l'algèbre au travers des œuvres de François Viète. Les premiers travaux du jeune Huygens touchent à l'élucidation des règles du choc. Il se penche très vite, dès 1652 sur les règles exposées par Descartes dans les Principes de la philosophie et qu'il pense incorrectes. Prenant appui sur la conservation cartésienne de la quantité de mouvement mv, il utilise astucieusement le principe de relativité pour changer de référentiel et parvient à déterminer les lois correctes du choc élastique. À cette occasion, il met en évidence la conservation des sommes des quantités mv ², sans lui donner de signification physique particulière^{[n 1]}. Il ne publie ces règles qu'avec retard, en 1669 lors d'un concours lancé par la Royal Society, où John Wallis et Christopher Wren donnent eux aussi des règles satisfaisantes, quoique moins générales.

En 1655, Huygens découvrit Titan, la lune de Saturne. Il examina également les anneaux de Saturne et établit qu'il s'agissait bien d'un anneau entourant la planète. En 1656, il découvrit que ces anneaux sont constitués de roches. La même année, il observa la nébuleuse d'Orion. En utilisant son télescope moderne, il put séparer la nébuleuse en différentes étoiles. La partie interne la plus lumineuse de la nébuleuse s'appelle actuellement la région de Huygens en son honneur. Il découvrit également plusieurs nébuleuses et quelques étoiles doubles.

Correspondance

Après avoir entendu parler de la correspondance de Blaise Pascal et Pierre de Fermat au sujet du problème des partis lors d'un voyage à Paris en 1655, Huygens, encouragé par Frans van Schooten, publia le premier livre sur le calcul des probabilités dans les jeux de hasard^[2] en 1657. Il y introduit comme notion fondamentale la valeur de l'espérance d'une situation d'incertitude. Ce livre, qu'il traduit en néerlandais en 1660, va jouer un rôle déterminant dans la diffusion de cette nouvelle mathématique ; il est repris en anglais (anonymement) par John Arbuthnot en 1692^[3], en latin par Juan Caramuel y Lobkowitz en 1670^[4], et de manière décisive par Jacques Bernoulli dans la première partie de son Ars conjectandi publié en 1715.

Portrait probable de Huygens (de face), détail de l'Établissement de l'Académie des Sciences et fondation de l'observatoire, 1666.

Entre 1658 et 1659, Huygens travaille à la théorie du pendule oscillant. Il a en effet l'idée de réguler des horloges au moyen d'un pendule, afin de rendre la mesure du temps plus précise. Il découvre la formule de l'isochronisme rigoureux en décembre 1659 : lorsque l'extrémité du pendule parcourt un arc de cycloïde, la période d'oscillation est constante quelle que soit l'amplitude. Contrairement à ce que Galilée avait cru démontrer dans les Discours et démonstrations mathématiques (en) de 1638, l'oscillation circulaire du pendule n'est pas parfaitement isochrone si l'on excède une amplitude de 5 degrés par rapport au point le plus bas.

Pour appliquer cette découverte aux horloges, il faut placer près du point de suspension du pendule deux « joues » cycloïdales qui contraignent la tige semi-rigide à parcourir elle-même une cycloïde. Bien évidemment l'ouvrage intitulé Horologium que Huygens publie en 1658 ne porte pas encore les fruits de cette découverte théorique et se contente de décrire un modèle innovant par sa régulation, et son système d'échappement, mais auquel il manque encore une maîtrise théorique qui ne sera publiée que dans l’Horologium Oscillatorium de 1673. Huygens détermine la période du pendule simple^{[n 2]}, qui s'exprime algébriquement sous la forme suivante (l étant la longueur du pendule, g la gravité et T la période) :

En 1659, Huygens découvre la formule donnant la force centrifuge, mais ne publie les théorèmes qu'il a découverts qu'en 1673. En 1666, il commence à concevoir que la force centrifuge due à la rotation de la Terre puisse avoir une influence sur une différence de pesanteur entre les pôles et l'équateur. Il s'intéresse aux résultats donnés par plusieurs expéditions dans les décennies qui suivent visant à détecter une telle différence. Vers 1690, en même temps que Newton, il pense que cette différence de pesanteur est incompatible avec une forme purement sphérique de la Terre et donne une estimation de l'aplatissement de celle-ci^[5],[6].

En 1665, Huygens découvre que deux horloges placées à proximité peuvent se synchroniser^[7],[8],[9].

Huygens est élu « fellow » de la Royal Society en 1663. En 1666, Huygens devient un membre éminent de l'Académie royale des sciences fondée par Colbert à Paris. Participant à la réalisation de l'Observatoire de Paris, achevé en 1672, il y effectue encore d'autres observations astronomiques.

Huygens est également connu pour ses arguments selon lesquels la lumière est composée d'ondes (voir : dualité onde-particule).

En réponse^{[réf. souhaitée]} aux articles d'Isaac Newton sur la lumière, en 1672, il se lance dans l'étude de la nature de la lumière, à la suite de savants tels que Rasmus Bartholin. Il découvre en 1677, grâce aux propriétés des cristaux et de leur coupe géométrique, en particulier grâce au spath d'Islande, que les lois de réflexion et de réfraction de Snell-Descartes sont conservées si l'on suppose une propagation de la lumière sous la forme d'ondes. En outre, la double réfraction du spath d'Islande peut être expliquée, ce qui n'est pas le cas avec une théorie corpusculaire.

La théorie ondulatoire, présentée en 1678 et publiée en 1690 dans son Traité de la Lumière, sous une forme encore très peu développée et vite éclipsée par les succès newtoniens, voyait alors le jour sous la plume d'auteurs tels que le P. Pardies^[10]. Augustin Fresnel en retrouvera le sens, plus tard, en toute indépendance puisqu'il ne semble pas avoir connu, pas plus que Young, les travaux de Huygens.

En 1673, Huygens et son jeune assistant Denis Papin, mettent en évidence le principe des moteurs à combustion interne, qui conduiront au XIX^e siècle à l'invention de l'automobile. Ils réussissent à déplacer un piston entraînant une charge de 70 kg sur 30 cm, en chauffant un cylindre métallique vidé d'air, empli de poudre à canon. Huygens est donc considéré comme le précurseur du moteur à combustion interne^[11].

Huygens retourna à La Haye en 1681 après une sérieuse maladie. Le décès de son protecteur Colbert en 1683 ne lui permet plus d'échapper à la révocation de l'Édit de Nantes aux courants de contre-Réforme qui agitent la France. Lui qui demeurait à Paris au moment même où Louis XIV avait déclaré la guerre aux Provinces-Unies, doit se résoudre à demeurer en sa résidence de Hofwijck et sur le Plein de La Haye pour les dernières années de sa carrière scientifique. C'est à cette époque qu'il rédige plusieurs manuscrits portant sur la nécessité de saisir d'une manière synthétique son œuvre, qui est finalement publiée dans son intégralité.

Il est aussi conduit à méditer sur les relations entre la science et la croyance en général. C'est à ce moment qu'il s'interroge sur la manière de conforter l'hypothèse copernicienne. Dans son livre Cosmotheoros, sive de terris coelestibus, earumque ornatu, conjecturae (La Haye, 1698) il illustre en deux parties les conséquences de la thèse copernicienne. Il se situe en cela dans la tradition ouverte par Pierre Borel, Cyrano de Bergerac, Galilée ou Gassendi. D'une part, il se livre à des conjectures relatives à la possibilité d'autres formes de vie dans un univers où chaque soleil est un autre monde. Cette réflexion le conduit à justifier l'existence de planéticoles au titre d'une conséquence de la grâce divine qui doit nécessairement s'étendre à l'ensemble de l'univers et ne pas se limiter à notre Terre.

Créationniste, Huygens récuse toute possibilité d'évolution ou de transformation des espèces et il ne peut concevoir de vie intelligente que sous une forme nettement anthropoïde. D'autre part, Huygens examine ce que pourraient être les « apparences » telles qu'elles seraient perçues par un observateur situé sur un autre centre de référence que le nôtre.^{[réf. nécessaire]}

C'était le climat libéral aux Pays-Bas qui a permis, en ce temps de progrès scientifiques, de telles spéculations.

Il meurt le 8 juillet 1695.

Le module faisant partie de la sonde Cassini et qui a atterri sur Titan a été baptisé du nom de Huygens. L'astéroïde (2801) Huygens a également été nommé en son honneur.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Christiaan Huygens » (voir la liste des auteurs).

Notes

Références

Voir aussi

Bibliographie

• Notices d’autorité : Fichier d’autorité international virtuel • International Standard Name Identifier • Union List of Artist Names • Bibliothèque nationale de France • Système universitaire de documentation • Bibliothèque du Congrès • Gemeinsame Normdatei • Bibliothèque nationale de la Diète • WorldCat

Ouvrages

• Christian Huygens, Traité de la lumière, où sont expliquées les causes de ce qui luy arrive dans la réflexion et dans la réfraction et particulièrement dans l'étrange réfraction du cristal d'Islande, avec un Discours de la cause de la pesanteur, Leipzig, Gressner et Schramm, texte en ligne disponible sur IRIS.

• Fabien Chareix, La philosophie naturelle de Christian Huygens, Vrin, coll. « Mathesis »,‎ 2006, 322 p. (ISBN 2-7116-1826-9, présentation en ligne)
• Christiane Vilain, La mécanique de Christian Huygens. La relativité du mouvement au XVII^e siècle. Paris, A. Blanchard, 1996. (Sciences dans l'histoire). 287p. (ISBN 2-85367-201-8).

Colloques et numéros de revues consacrés à l’œuvre de Huygens

• « Expérience et raison. La science chez Huygens », Revue d’histoire des sciences, n^o 1,‎ 2003 (ISBN 2-13-053769-3, ISSN 0151-4105, lire en ligne)
  Ce numéro contient les articles suivants :
  • Fabien Chareix, Experientia ac ratio: L'œuvre de Christiaan Huygens, in : Revue d'histoire des sciences 56-1 (2003), p. 5-13.
  • F. Chareix, La découverte des lois du choc par Christiaan Huygens, in : Revue d'histoire des sciences 56-1 (2003), p. 15-58.
  • André Charrak, Huygens et la théorie musicale, in : Revue d'histoire des sciences 56-1 (2003), p. 59-78.
  • Patricia Radelet-de Grave, L'univers selon Huygens, le connu et l'imaginé, in : Revue d'histoire des sciences 56-1 (2003), p. 79-112.
  • Gianfranco Mormino, Le rôle de Dieu dans l'œuvre scientifique et philosophique de Christiaan Huygens, in : Revue d'histoire des sciences 56-1 (2003), p. 113-133.
  • G. Mormino, Sur quelques problèmes éditoriaux concernant l'œuvre de Christiaan Huygens, in : Revue d'histoire des sciences 56-1 (2003), p. 145-151.
• Centre national de la recherche scientifique (Paris). Table ronde (1979-03-27 ; Paris), Huygens et la France, Vrin, coll. « L'Histoire des sciences »,‎ 1982, 268 p. (ISBN 2-7116-2018-2, présentation en ligne)

Articles divers

• Michel Blay, Christiaan Huygens et les phénomènes de la couleur, in : Revue d'histoire des sciences 37-2 (1984), p. 127-150.
• Daniel Parrochia, Optique, mécanique et calcul des chances chez Huygens et Spinoza, in : Dialectica-Lausanne 38-4 (1984), p. 319-345.
• Christine Vilain, « La loi galiléenne et la dynamique de Huygens », Revue d’histoire des mathématiques, vol. 2, n^o 1,‎ 1996, p. 95-117 (lire en ligne).

Articles connexes

• Inégalité de Huygens
• Mathématiques en Europe au XVIIe siècle
• Micro-intervalle
• Principe de Huygens-Fresnel (optique)
• Transport du moment d'inertie (mécanique)
• Histoire de l'horlogerie

Liens externes

• Ouvrage de Huygens numérisé par le SCD de l'Université de Strasbourg
• Bibliographie de C. Huygens sur le site Origine des Rationalités à l'Age Classique (ORACL)
• Huyghens, Young, Fresnel, Maxwell, la lumière et l'électricité.

• Portail de la physique
• Portail de l’astronomie
• Portail des mathématiques
• Portail de l’optique
• Portail de la France du Grand Siècle
• Portail des Pays-Bas