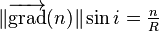Principe de Fermat
Le principe de Fermat est un principe physique, attribué à Pierre de Fermat, qui sert de fondement à l'optique géométrique. Il décrit la forme du chemin optique d'un rayon lumineux et s'énonce ainsi :
La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit localement minimale (localement signifiant : pour une trajectoire "petite").
Une conséquence première du principe de Fermat est la propagation rectiligne des rayons lumineux dans les milieux homogènes. En effet, dans un milieu homogène, le temps de parcours est proportionnel à la longueur du trajet, et le chemin le plus court dans un espace euclidien pour aller d’un point à un autre est la ligne droite.
Il permet de retrouver la plupart des résultats de l'optique géométrique, en particulier les lois de la réflexion sur les miroirs, les lois de la réfraction, la loi de Snell-Descartes, etc.
Historique
Ce principe doit son nom à Pierre de Fermat, qui l'a énoncé en 1657 mais qui n'a soumis son mémoire, Synthèse pour les réfractions qu'en 1662. Tandis que René Descartes, dans La Dioptrique, expliquait les lois de l'optique en faisant « l'analogie entre les rayons lumineux et les trajectoires d'une balle envoyée par un joueur de paume[1] », Fermat se base sur un principe moral :« La nature agit toujours par les voies les plus courtes et les plus simples[2]. »
En 1740, Pierre Louis Moreau de Maupertuis en complète la conception en créant le principe de Maupertuis qui, une fois peaufiné par Joseph Louis Lagrange, devint le principe de moindre action[3].
En 1924, Louis de Broglie fit une synthèse du principe de Fermat et de celui de moindre action en proposant qu'à chaque particule massive soit associée une onde : cela ouvrit la voie de la dualité onde-particule menant à l'équation de Schrödinger, fondamentale en mécanique quantique[3].
Durées de parcours stationnaires ou minimales
Le principe de Fermat a été énoncé ci-dessus sous sa forme commune mais on doit l'énoncer sous la forme plus rigoureuse :
La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit stationnaire.
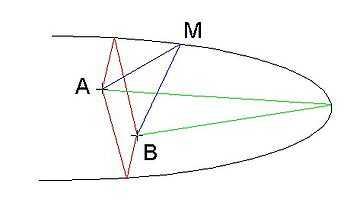
En effet si, dans la plupart des cas, on rencontre des chemins dont la durée de parcours est minimale, il ne faut pas oublier pour autant que d'autres situations peuvent exister. Par exemple, pour aller d'un point A à un point B situés à l'intérieur du miroir concave représenté ci-contre, en se réfléchissant une seule fois sur la surface, la lumière peut emprunter deux parcours de durée minimale (en rouge) et un parcours de durée maximale (en vert) parmi les parcours constitués de deux segments AM et BM. L'étude de la longueur du chemin 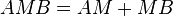 ferait apparaître trois extrema locaux, deux minima et un maximum, pour ce type de trajets.
ferait apparaître trois extrema locaux, deux minima et un maximum, pour ce type de trajets.
Le terme stationnaire peut être compris à partir de cet exemple. Si le point quelconque M effectue un déplacement infiniment petit du premier ordre à la surface du miroir, la variation du chemin optique est également du premier ordre. En revanche, si l'on considère les trois zones qui correspondent aux extrema, alors un déplacement du premier ordre du point entraîne une variation du chemin optique du second ordre ou plus faible encore. En d'autres termes, lorsque le point M se déplace sur le miroir, la variation du chemin optique est rapide presque partout mais très lente au voisinage des trois points particuliers où elle devient quasi nulle, d'où l'emploi du mot « stationnaire ».
Toutefois, si deux points sont reliés par un chemin suffisamment court, ce chemin minimise la durée par rapport aux autres chemins possibles les plus proches. Pour reprendre l'exemple du miroir concave, si les deux points sont sur le trajet vert et sont assez proches de son point de « rebond » sur le miroir concave, alors pour la longueur du chemin 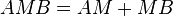 il n'y a plus trois extrema, mais un seul qui est un minimum. De manière générale, une trajectoire pour la lumière entre deux points est un point col ou un minimum pour l'ensemble des trajectoires géométriquement possibles les reliant[4].
il n'y a plus trois extrema, mais un seul qui est un minimum. De manière générale, une trajectoire pour la lumière entre deux points est un point col ou un minimum pour l'ensemble des trajectoires géométriquement possibles les reliant[4].
Le même problème se retrouve dans l'énoncé du principe de moindre action, qui est à la mécanique ce qu'est le principe de Fermat à l'optique, dans la définition des surfaces minimales (qui ne sont pas forcément... minimales) ou dans celle des géodésiques.
Formulation du principe de Fermat à l’aide du chemin optique
Cas d’un milieu homogène
Le chemin optique de la lumière pour aller d'un point  vers un point
vers un point 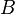 dans un milieu homogène, noté
dans un milieu homogène, noté 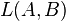 , est défini comme étant un nombre proportionnel au temps mis par le rayon pour aller de
, est défini comme étant un nombre proportionnel au temps mis par le rayon pour aller de  à
à 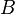 , le coefficient de proportionnalité étant tel que
, le coefficient de proportionnalité étant tel que 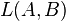 est égal à la distance
est égal à la distance 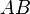 pour un parcours dans le vide. Appelant
pour un parcours dans le vide. Appelant 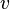 la célérité de la lumière dans le milieu, et
la célérité de la lumière dans le milieu, et  celle dans le vide, on a donc
celle dans le vide, on a donc 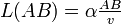 et
et 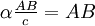 , d’où
, d’où 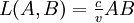 ; le coefficient de proportionnalité
; le coefficient de proportionnalité 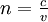 est appelé l’indice de réfraction du milieu.
Le chemin optique est donc défini par :
est appelé l’indice de réfraction du milieu.
Le chemin optique est donc défini par :
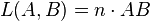
La lumière se propage « plus difficilement » dans les milieux autres que le vide.
Exemple : Un rayon lumineux traverse une couche d'eau de 5 cm d'épaisseur. Parallèlement, un autre rayon lumineux traverse 5 cm d'air. L'eau a pour indice de réfraction 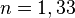 et l'air un indice sensiblement égal à celui du vide
et l'air un indice sensiblement égal à celui du vide 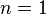 . Dans l'eau, le rayon lumineux aura parcouru une distance
. Dans l'eau, le rayon lumineux aura parcouru une distance 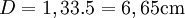 . Dans l'air, le rayon aura parcouru une distance
. Dans l'air, le rayon aura parcouru une distance 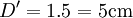 . Le rayon aura parcouru un chemin optique plus long dans l'eau que dans l'air.
. Le rayon aura parcouru un chemin optique plus long dans l'eau que dans l'air.
Cas d'un milieu continu quelconque
On considère deux points infiniment voisins et distants d'une distance 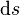 .
Le chemin optique séparant ces deux points est défini par
.
Le chemin optique séparant ces deux points est défini par 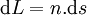 ;
; 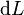 est la différentielle de chemin optique ou encore, l'élément unitaire infinitésimal de chemin optique. Pour trouver le chemin optique
est la différentielle de chemin optique ou encore, l'élément unitaire infinitésimal de chemin optique. Pour trouver le chemin optique 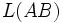 séparant deux points
séparant deux points  et
et 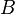 sur cette courbe, il suffit de faire la somme intégrale de tous les éléments
sur cette courbe, il suffit de faire la somme intégrale de tous les éléments 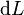 sur la coordonnée curviligne
sur la coordonnée curviligne  délimitée par les points
délimitée par les points  et
et 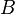 :
:
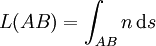
Le principe de Fermat s’énonce alors :
Entre deux pointset
, atteints par la lumière, le chemin optique suivi le long du trajet est stationnaire.
Conséquences
Principe du retour inverse de la lumière
Le trajet suivi par la lumière pour aller d'un point à un autre ne dépend pas du sens de propagation de la lumière.
La stationnarité du chemin optique permet de procéder à quelques considérations. Entre deux points A et B, tous deux sur la trajectoire curviligne d'un rayon lumineux se propageant dans un milieu inhomogène, on peut exprimer l'intégrale de chemin optique comme il suit :
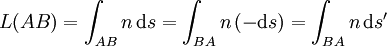
En considérant que 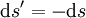 est l'élément de coordonnée curviligne de B vers A, on peut alors écrire
est l'élément de coordonnée curviligne de B vers A, on peut alors écrire 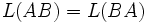 .
Dans le cas de l'étude d'un système optique, cela signifie que l'on pourra étudier la propagation de la lumière et le trajet des rayons lumineux sans se soucier du sens de propagation.
.
Dans le cas de l'étude d'un système optique, cela signifie que l'on pourra étudier la propagation de la lumière et le trajet des rayons lumineux sans se soucier du sens de propagation.
Attention : en pratique, l'utilisation irréfléchie de ce principe aboutit à des absurdités. On sait par exemple qu'un objectif ne donne jamais une image ponctuelle d'un point lumineux, mais une tache toujours plus ou moins floue. Il serait enfantin de penser que les rayons formant cette tache, renvoyés dans l'objectif par un miroir plan, pourraient reformer de l'autre côté un point-image net ... Ce n'est pas le principe qui est en cause ici, mais le fait de vouloir l'appliquer de façon fautive.
Lois de Snell-Descartes
Un plan  de vecteur normal
de vecteur normal 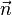 sépare deux milieux d’indices de réfractions
sépare deux milieux d’indices de réfractions 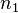 et
et 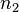 . Un rayon lumineux part d'un point
. Un rayon lumineux part d'un point 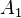 situé dans le premier milieu, traverse
situé dans le premier milieu, traverse  en
en 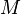 et atteint un point
et atteint un point 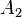 . Le problème est de trouver la position de
. Le problème est de trouver la position de 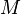 à partir du principe de Fermat.
à partir du principe de Fermat.
Le chemin optique de 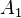 à
à 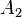 est
est 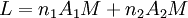 donc :
donc :
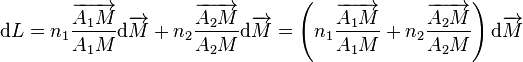
La condition de stationnarité de  ,
,  , se traduit donc par le fait que
, se traduit donc par le fait que  est orthogonal au plan
est orthogonal au plan  , soit colinéaire à
, soit colinéaire à 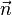 ; le rayon lumineux est donc inclus dans le plan passant par
; le rayon lumineux est donc inclus dans le plan passant par 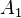 et
et 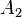 et orthogonal à
et orthogonal à  (première loi de Descartes) et
(première loi de Descartes) et 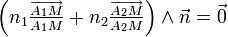 donne :
donne : 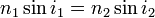 (deuxième loi de Descartes).
(deuxième loi de Descartes).
Cette démonstration est due essentiellement à Maupertuis en 1744, près d’un siècle après l’énoncé par Fermat de son principe.
Une jolie illustration en est donnée par le problème dit « du maître-nageur ». Celui-ci, situé sur la plage en  doit aller secourir un noyé situé en
doit aller secourir un noyé situé en  . Comme il court plus vite qu'il ne nage, son trajet optimal (en temps) est celui qui suit les lois de la réfraction, que nous venons de déterminer.
. Comme il court plus vite qu'il ne nage, son trajet optimal (en temps) est celui qui suit les lois de la réfraction, que nous venons de déterminer.
On démontre que si la surface de séparation des deux milieux est une surface quelconque, les deux lois de Descartes sont conservées (mais il peut y avoir plusieurs chemins possibles).
Généralisation des lois de Descartes au cas d’un milieu continu quelconque
Cas d'un trajet plan
Si la lumière se déplace dans un plan  , on peut paramétrer sa trajectoire par son abscisse x (à l'exception de la droite x=constante). La trajectoire devient une fonction y(x) et le chemin optique s'écrit
, on peut paramétrer sa trajectoire par son abscisse x (à l'exception de la droite x=constante). La trajectoire devient une fonction y(x) et le chemin optique s'écrit
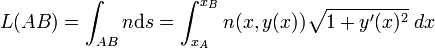
L’équation d'Euler-Lagrange exprimant la stationnarité de cette intégrale donne
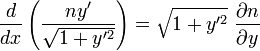
Nous allons résoudre le cas particulier où n ne dépend que de x : on obtient alors 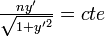 ; or si on désigne par
; or si on désigne par 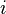 l’angle que fait la tangente à la courbe avec
l’angle que fait la tangente à la courbe avec 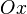 , cette condition s’écrit :
, cette condition s’écrit :
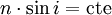
Ceci constitue en quelque sorte une version infinitésimale de la seconde loi de Descartes, laquelle est en fait une traduction locale du principe de Fermat.
L’équation différentielle de la trajectoire est donc : 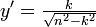 .
.
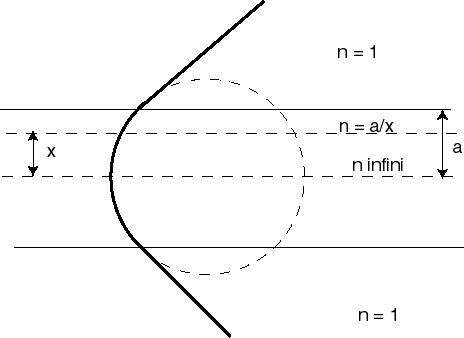
On retrouve évidemment que pour 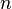 constant, les trajectoires sont des droites ; mais si on prend
constant, les trajectoires sont des droites ; mais si on prend 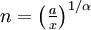 , la courbe se paramétrise simplement en
, la courbe se paramétrise simplement en
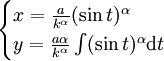 .
.C'est une courbe de Ribaucour.
Par exemple pour 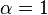 (l'indice de réfraction est inversement proportionnel à l'abscisse) on obtient
(l'indice de réfraction est inversement proportionnel à l'abscisse) on obtient
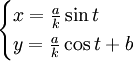 ,
,autrement dit les trajectoires sont des cercles.
Pour 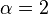 (l'indice de réfraction est inversement proportionnel à la racine carrée de l'abscisse) on obtient
(l'indice de réfraction est inversement proportionnel à la racine carrée de l'abscisse) on obtient
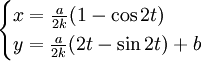 :
:la courbe est une cycloïde. Ce cas est historiquement intéressant : c'est par cette méthode que Jean Bernoulli a prouvé que la courbe brachistochrone (minimisant le temps de parcours d'un point matériel) est la cycloïde, en montrant que le problème de mécanique et celui d'optique sont en fait équivalents.
Cas général
On considère maintenant un milieu hétérogène continu à 3 dimensions. On montre que les lois de Descartes généralisées, issues du principe de Fermat, s'énoncent sous la forme suivante :
- Le plan osculateur à la trajectoire en un point
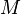 contient la normale à la surface d'indice de réfraction constant passant par
contient la normale à la surface d'indice de réfraction constant passant par 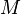 .
. - Si on désigne par
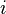 l’angle que fait la tangente à la courbe avec cette normale, on a la relation :
l’angle que fait la tangente à la courbe avec cette normale, on a la relation :
où 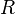 est le rayon de courbure de la courbe.
est le rayon de courbure de la courbe.
Notes et références
- ↑ Bernard Pire, « La Dioptrique (R. Descartes) », sur Encyclopædia universlis (consulté le 20 mars 2015).
- ↑ Giorello G, L'économie de la nature, Les génies de la science, août-septembre 2007, p56-65
- 1 2 Histoire du principe de moindre action par Florence Martin-Robine, chez Vuibert, 2006
- ↑ Voir le chapitre 3, p117-134, et les exercices E3.4 et E3.5, p144-145, du livre Mécanique : de la formulation lagrangienne au chaos hamiltonien de Claude Gignoux et Bernard Silvestre-Brac, éditeur EDP-Sciences, 2002, ISBN 2868835848
Voir aussi
Bibliographie
- José Philipe Pérez, Optique : fondements et application
- Ouvrage de mécanique générale des Séries Schaum
- Born & Wolf, Principles of optics
- Georges Bruhat, Optique
- Jean Bass, Exercices de mathématiques, Masson, 1965, p. 381-385
Articles connexes
- Réfraction
- Principe de moindre action
Liens externes
- Le chapitre du Wikilivre de photographie sur la propagation de la lumière et plus spécialement sur le principe de Fermat.
- Jean Gounon, Principe de Fermat : Applications à la réflexion et à la réfraction (fichier PDF)
- Une démonstration géométrique due à Huygens du principe de Fermat appliqué à la réfraction.
- Portail de la physique
- Portail de l’optique