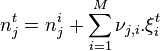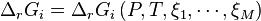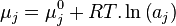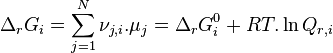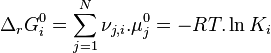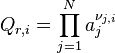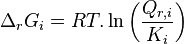Équilibre chimique
|
Équilibre chimique
| |
| Notions de base | |
|---|---|
| Équation bilan de la réaction chimique | 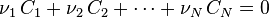 Coefficients stœchiométriques :
|
| Avancement de réaction | Variation des quantités des réactifs et produits :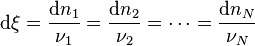 |
| Deuxième principe de la thermodynamique | Enthalpie libre  Évolution spontanée à pression et température constantes : 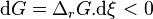 |
| Condition d'équilibre | 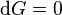 |
| Réaction à pression et température constantes | |
| Enthalpie libre de réaction |  |
| Potentiels chimiques | 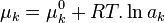 |
| Constante d'équilibre | Enthalpie libre standard de réaction :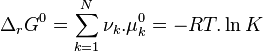 Potentiels chimiques à l'état standard |
| Quotient de réaction | 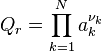 , activités chimiques , activités chimiques |
| Développement | 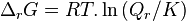 |
| Progression de la réaction | Déplacement des réactifs vers les produits :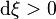 , , 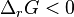 , , 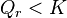 |
| Régression de la réaction | Déplacement des produits vers les réactifs :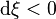 , ,  , , 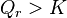 |
| Condition d'équilibre labile | 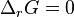 Loi d'action de masse : 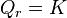 |
| Condition de stabilité | 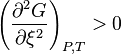 , , 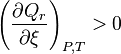 |
| Déplacement d'un équilibre chimique | |
| Principe de modération de Le Chatelier | Lorsque les modifications extérieures apportées à un système physico-chimique en équilibre provoquent une évolution vers un nouvel état d'équilibre, l'évolution s'oppose aux perturbations qui l'ont engendrée et en modère l'effet. |
| Augmentation de la température | À pression constante, déplacement dans le sens endothermique. |
| Augmentation de la pression | À température constante, déplacement dans le sens d'une diminution de la quantité totale de constituants, du volume. |
| Ajout d'un réactif ou d'un produit | Pas de règle générale, le principe de modération (déplacement dans le sens de la consommation du réactif ou du produit ajouté) est souvent observé mais n'est pas systématique. |
| Ajout d'un inerte | À pression et température constantes, déplacement dans le sens d'une augmentation de la quantité totale de constituants, du volume. |
| À volume et température constants, absence de conséquence. | |
| Emploi d'un catalyseur | L'équilibre est atteint plus vite, mais il n'est pas déplacé. |
Un équilibre chimique est le résultat de deux réactions chimiques antagonistes simultanées dont les effets s'annulent mutuellement.
Une réaction telle que la combustion du propane avec l'oxygène, s'arrêtant lorsque l'un des réactifs est totalement épuisé, est qualifiée de réaction totale, complète ou irréversible. A contrario, une réaction comme l'estérification, aboutissant à un mélange stable dans le temps de réactifs et de produits, sans disparition totale de l'une des espèces, est qualifiée de réaction partielle, incomplète, réversible ou inversible[1] : ce type de réaction aboutit à un équilibre chimique. Au cours d'un processus de transformation chimique deux réactions peuvent s'opposer, l'une consommant des réactifs, l'autre consommant les produits de la première réaction pour recréer les réactifs initiaux. Une réaction est totale lorsqu'elle l'emporte sur sa réaction antagoniste. Un équilibre chimique apparaît lorsque la première réaction consomme les réactifs aussi vite que la seconde les recrée. De plus, une modification des conditions opératoires d'un équilibre chimique (modification de la pression ou de la température, ajout ou extraction de l'un des constituants du mélange réactionnel, etc.) pourra favoriser l'une ou l'autre réaction, impliquant un déplacement de l'équilibre, c'est-à-dire l'obtention d'un nouvel état d'équilibre à une composition différente de celle de l'équilibre initial ; un retour aux conditions opératoires initiales induira un retour à l'équilibre initial. Dans certains cas, la modification des conditions opératoires pourra conduire à une rupture d'équilibre, c'est-à-dire l'obtention d'une réaction totale.
La notion d'équilibre chimique fut pour la première fois évoquée en 1803 par Berthollet à la suite de ses observations sur les rives du lac Natron lors de la campagne d'Égypte. Avant lui, les réactions chimiques étaient supposées être toujours totales[2],[3]. Il fallut cependant attendre la deuxième moitié du XIXe siècle pour que des progrès significatifs soient faits dans la compréhension des réactions et équilibres chimiques. En 1858 Kirchhoff énonçait ses relations liant variation de la chaleur d'une réaction chimique et différence des capacités calorifiques des produits et des réactifs. En 1865 Guldberg et Waage, en s'inspirant des propositions de Berthollet, montrèrent expérimentalement qu'il existait une relation entre les concentrations des espèces présentes à l'équilibre en solution ; la constante d'équilibre 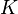 qu'ils définirent a été appelée constante de Guldberg et Waage ou constante de la loi d'action de masse. Un premier formalisme mathématique des équilibres chimiques fut développé par van 't Hoff, qui énonça la relation portant son nom donnant la variation de
qu'ils définirent a été appelée constante de Guldberg et Waage ou constante de la loi d'action de masse. Un premier formalisme mathématique des équilibres chimiques fut développé par van 't Hoff, qui énonça la relation portant son nom donnant la variation de 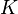 en fonction de la chaleur de la réaction. En 1884, Le Chatelier, toujours sur base d'expérimentations, énonçait son « principe de modération », dit « principe de Le Chatelier », selon lequel un équilibre s'oppose aux changements extérieurs qui tentent de le modifier. Il existe cependant des cas dans lesquels ce principe n'est pas vérifié, notamment pour l'ajout ou l'extraction d'une espèce du mélange réactionnel.
en fonction de la chaleur de la réaction. En 1884, Le Chatelier, toujours sur base d'expérimentations, énonçait son « principe de modération », dit « principe de Le Chatelier », selon lequel un équilibre s'oppose aux changements extérieurs qui tentent de le modifier. Il existe cependant des cas dans lesquels ce principe n'est pas vérifié, notamment pour l'ajout ou l'extraction d'une espèce du mélange réactionnel.
Le développement ultérieur du formalisme mathématique de la thermodynamique par Gibbs (qui introduisit la fonction enthalpie libre  et la notion de potentiel chimique
et la notion de potentiel chimique 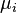 ), de Donder (qui définit l'avancement de réaction
), de Donder (qui définit l'avancement de réaction 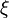 et l'affinité chimique
et l'affinité chimique 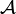 , reliant l'évolution des réactions chimiques au deuxième principe de la thermodynamique) et Lewis (qui introduisit la notion d'activité chimique
, reliant l'évolution des réactions chimiques au deuxième principe de la thermodynamique) et Lewis (qui introduisit la notion d'activité chimique 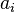 ) a permis en 1950[4] à Prigogine et Defay[5] de démontrer rigoureusement les relations et principes formulés par Kirchhoff, van 't Hoff, Guldberg, Waage et Le Chatelier. Ce formalisme est développé dans cet article qui définit les grandeurs permettant :
) a permis en 1950[4] à Prigogine et Defay[5] de démontrer rigoureusement les relations et principes formulés par Kirchhoff, van 't Hoff, Guldberg, Waage et Le Chatelier. Ce formalisme est développé dans cet article qui définit les grandeurs permettant :
- de positionner l'équilibre :
- enthalpie libre standard de réaction :
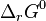 ;
; - constante d'équilibre :
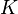 ;
;
- enthalpie libre standard de réaction :
- de prédire l'évolution de la réaction hors équilibre :
- enthalpie libre de réaction :
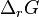 ;
; - quotient de réaction :
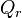 .
.
- enthalpie libre de réaction :
Notions de base
Principe de Berthelot, principe de Matignon
Une réaction chimique est favorisée ou défavorisée par divers facteurs tels que la pression, la température, l'énergie apportée au mélange réactionnel. L'étude des réactions chimiques et des équilibres a conduit, dans la seconde moitié du XIXe siècle, à l'énoncé des deux principes empiriques suivants[6],[7],[8] :
« Principe de Berthelot[9] - Facteur énergétique
Un système laissé à lui-même tend à évoluer de manière à libérer le plus de chaleur. »
Autrement dit, une réaction est favorisée si elle est exothermique, elle est défavorisée si elle est endothermique. Les réactions exothermiques ayant une très forte chaleur de réaction (enthalpie standard de réaction 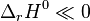 ), comme les réactions de combustion, sont souvent totales.
), comme les réactions de combustion, sont souvent totales.
« Principe de Matignon - Facteur désordre
Une réaction chimique évolue dans le sens de l'augmentation du nombre de ses molécules. »
Les réactions augmentant la quantité de matière dans le mélange réactionnel sont favorisées : la réaction de combustion d'un alcane avec l'oxygène est favorisée, car le nombre de moles de produits est supérieur à celui des réactifs ; en outre elle est exothermique, elle est donc doublement favorisée ce qui la rend totale. Le principe de Matignon est en accord avec le deuxième principe de la thermodynamique : les réactions dont l'entropie standard de réaction 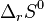 est positive sont favorisées, or une augmentation du nombre de moles d'un système thermodynamique à la suite d'une réaction correspond à une augmentation de l'entropie. Les réactions produisant un gaz à partir d'un solide sont donc également favorisées, car l'entropie d'un gaz est plus élevée que celle d'un solide[10].
est positive sont favorisées, or une augmentation du nombre de moles d'un système thermodynamique à la suite d'une réaction correspond à une augmentation de l'entropie. Les réactions produisant un gaz à partir d'un solide sont donc également favorisées, car l'entropie d'un gaz est plus élevée que celle d'un solide[10].
Lorsque ces deux principes, qui en eux-mêmes n'ont qu'un intérêt historique, entrent en concurrence au sein d'une même réaction, il apparaît un équilibre. Leur combinaison, qui fut effectuée par Gibbs et Duhem[11], conduit à l'étude de l'enthalpie libre standard de réaction 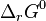 , définie par :
, définie par :
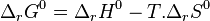
- lorsque
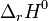 et
et 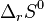 sont de signes opposés, les deux principes sont simultanément favorables ou défavorables :
sont de signes opposés, les deux principes sont simultanément favorables ou défavorables :
- si
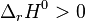 et
et  , soit
, soit 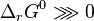 , selon les deux principes tous les facteurs sont défavorables : la réaction est impossible ;
, selon les deux principes tous les facteurs sont défavorables : la réaction est impossible ; - si
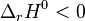 et
et 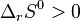 , soit
, soit 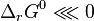 , selon les deux principes tous les facteurs sont favorables : la réaction est totale ;
, selon les deux principes tous les facteurs sont favorables : la réaction est totale ;
- si
- lorsque
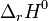 et
et 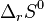 sont de même signe, les deux principes s'opposent, le signe de
sont de même signe, les deux principes s'opposent, le signe de 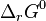 peut être positif ou négatif : la réaction conduit à un équilibre d'autant plus déplacé que
peut être positif ou négatif : la réaction conduit à un équilibre d'autant plus déplacé que 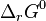 est éloigné de 0 :
est éloigné de 0 :
- si
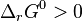 la réaction est peu favorisée, l'équilibre contiendra majoritairement des réactifs, peu consommés ;
la réaction est peu favorisée, l'équilibre contiendra majoritairement des réactifs, peu consommés ; - si
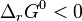 la réaction est favorisée, l'équilibre contiendra majoritairement des produits, les réactifs étant en grande partie consommés.
la réaction est favorisée, l'équilibre contiendra majoritairement des produits, les réactifs étant en grande partie consommés.
- si
Le tableau suivant récapitule l'influence des deux facteurs sur la réaction.
| Facteurs influant sur la réaction |
Principe de Matignon | ||
|---|---|---|---|
Augmentation du désordre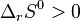 favorable |
Diminution du désordre défavorable | ||
| Principe de Berthelot |
Réaction exothermique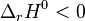 favorable |
Réaction totale |
Équilibre exothermique |
Réaction endothermique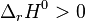 défavorable |
Équilibre endothermique |
Réaction impossible | |
Exemple - Équilibre du dioxyde et du trioxyde de soufre :
- La réaction de synthèse du trioxyde de soufre à partir du dioxyde de soufre s'écrit :
- La chaleur de réaction est de
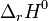 = –197,78 kJ/mol : la réaction est exothermique, elle est donc favorisée selon le principe de Berthelot. Cependant le nombre de constituants décroît selon cette réaction : pour 3 moles de réactifs il ne reste que 2 moles de produit, le principe de Matignon stipule donc que cette réaction n'est pas favorisée.
= –197,78 kJ/mol : la réaction est exothermique, elle est donc favorisée selon le principe de Berthelot. Cependant le nombre de constituants décroît selon cette réaction : pour 3 moles de réactifs il ne reste que 2 moles de produit, le principe de Matignon stipule donc que cette réaction n'est pas favorisée.
- Si l'on écrit la réaction dans le sens inverse, les facteurs sont inversés :
- Cette réaction est endothermique et donc n'est pas favorisée selon le principe de Berthelot, mais elle accroît le désordre et est donc favorisée selon le principe de Matignon.
- Les deux principes s'opposant, il s'ensuit un équilibre noté :
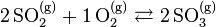
Réaction directe et réaction inverse, cinétique des réactions


Un équilibre chimique implique deux réactions simultanées :
- une réaction dans le sens réactifs → produits appelée réaction directe, il s'agit généralement de la réaction intéressante pour la production d'une espèce chimique donnée ;
- une réaction dans le sens produits → réactifs appelée réaction inverse, qui s'oppose à la réaction directe.
Dans un équilibre, l'une des deux réactions obéit au principe de Berthelot et l'autre au principe de Matignon : si l'une est exothermique, l'autre augmente le désordre du système réactionnel ; en conséquence, puisque les deux réactions ont des effets inverses, la première enfreint le principe de Matignon en diminuant le désordre, et la deuxième enfreint le principe de Berthelot en étant endothermique. Lorsqu'une réaction est équilibrée, cela signifie que la vitesse de la réaction directe est égale à la vitesse de la réaction inverse. L'état d'équilibre obtenu dans ce cas peut être qualifié d'équilibre dynamique ou stationnaire : les réactions ont toujours lieu, mais globalement leurs effets s'annulent ; par exemple la réaction directe consomme les réactifs aussi vite que la réaction inverse les recrée, d'où une composition du mélange réactionnel stable dans le temps ; ou encore la réaction endothermique absorbe totalement la chaleur dégagée par la réaction exothermique, d'où un bilan énergétique globalement nul.
Dans le cas d'un équilibre impliquant deux réactifs 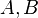 et deux produits
et deux produits 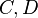 , on note l'équilibre sous la forme :
, on note l'équilibre sous la forme :
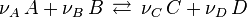
où 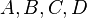 sont des espèces chimiques,
sont des espèces chimiques, 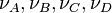 les coefficients stœchiométriques.
les coefficients stœchiométriques.
Dans le cas de réactions élémentaires, c'est-à-dire s'effectuant en une seule étape, les vitesses de réaction dépendent des concentrations ![[A],[B],[C],[D]](../i/m/78267131fa1a716d46271ee96b2a9ed4.png) des espèces en présence et de
des espèces en présence et de  les constantes respectives des vitesses des réactions directe et inverse (qui suivent la loi d'Arrhenius) selon les expressions :
les constantes respectives des vitesses des réactions directe et inverse (qui suivent la loi d'Arrhenius) selon les expressions :
-
![v_1 = k_1 . [A]^{\nu_A}.[B]^{\nu_B}](../i/m/17327a29f67a4c2c4ee1b762ec738605.png) , vitesse de la réaction directe ;
, vitesse de la réaction directe ; -
![v_2 = k_2 . [C]^{\nu_C}.[D]^{\nu_D}](../i/m/9b7176faa2c0984a871859bb53ea3758.png) , vitesse de la réaction inverse.
, vitesse de la réaction inverse.
Dans une réaction totale, la réaction inverse est inexistante, ou du moins a-t-elle une vitesse négligeable devant la vitesse de la réaction directe 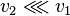 . À la fin d'un réaction totale, c'est-à-dire lorsque les concentrations des réactifs et produits ne varient plus, les réactifs ont totalement disparus s'ils ont été introduits à la stœchiométrie, sinon c'est le réactif introduit en défaut, ou réactif minoritaire, qui a totalement disparu.
. À la fin d'un réaction totale, c'est-à-dire lorsque les concentrations des réactifs et produits ne varient plus, les réactifs ont totalement disparus s'ils ont été introduits à la stœchiométrie, sinon c'est le réactif introduit en défaut, ou réactif minoritaire, qui a totalement disparu.
Dans un équilibre chimique, la vitesse de déplacement de l'équilibre est égale à la différence entre la vitesse de la réaction directe et la vitesse de la réaction inverse : 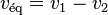 . Les deux vitesses de réaction finissent par s'égaliser sans s'annuler
. Les deux vitesses de réaction finissent par s'égaliser sans s'annuler 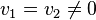 (c'est la vitesse de l'équilibre qui s'annule
(c'est la vitesse de l'équilibre qui s'annule 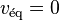 ). Ceci entraîne, à l'équilibre, la relation suivante, appelée loi d'action de masse :
). Ceci entraîne, à l'équilibre, la relation suivante, appelée loi d'action de masse :
![\frac {k_1}{k_2} = \frac {[C]^{\nu_C}.[D]^{\nu_D}}{[A]^{\nu_A}.[B]^{\nu_B}} = K](../i/m/8d9b04b631586cc632a4747151315a7a.png)
Cette relation lie les constantes des vitesses des deux réactions aux concentrations des réactifs et des produits à l'équilibre. Le rapport ainsi obtenu est appelé constante d'équilibre. Cette relation a été établie empiriquement par Guldberg et Waage. Nous verrons par la suite comment établir rigoureusement cette relation selon les principes de la thermodynamique. Dans un équilibre chimique aucune espèce, que ce soit un réactif ou un produit, ne disparaît totalement.
À noter que les expressions correctes des vitesses de réaction et de la constante d'équilibre doivent faire intervenir les activités chimiques des constituants, et non leur concentration ou leur pression molaire partielle souvent utilisées par approximation.
Avancement de réaction
Considérons un équilibre chimique réalisé à température et pression constantes dont l'équation bilan est la suivante :
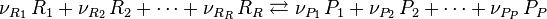
Les constituants 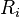 du membre de gauche sont les réactifs, au nombre de
du membre de gauche sont les réactifs, au nombre de 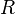 ; les constituants
; les constituants  du membre de droite sont les produits, au nombre de
du membre de droite sont les produits, au nombre de  :
:
-
![i \in [1,\cdots,R]](../i/m/e99c52b80103b2bf1e27fa66817a9061.png) réactif ;
réactif ; -
![j \in [1,\cdots,P]](../i/m/73922ea86ae502df26430df1da22bd3c.png) produit.
produit.
Considérons une petite progression de la réaction et appelons 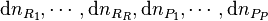 les variations élémentaires du nombre de moles de chaque constituant, à ce stade de la réaction. La réaction progresse en respectant la stœchiométrie de l'équation bilan, aussi si la quantité du réactif
les variations élémentaires du nombre de moles de chaque constituant, à ce stade de la réaction. La réaction progresse en respectant la stœchiométrie de l'équation bilan, aussi si la quantité du réactif 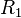 varie de
varie de 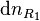 :
:
- la quantité de tout réactif
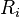 varie de :
varie de : 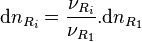 ;
; - la quantité de tout produit
 varie de :
varie de : 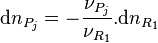 ;
;
ce qui implique que tous les rapports 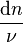 sont égaux au signe près :
sont égaux au signe près :

Le paramètre 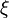 est appelé état d'avancement de la réaction, il est donc être défini sur l'un quelconque des constituants et il existe une relation entre
est appelé état d'avancement de la réaction, il est donc être défini sur l'un quelconque des constituants et il existe une relation entre 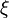 et chaque constituant. La connaissance de
et chaque constituant. La connaissance de 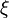 permet de connaître la composition du système : c'est une variable de composition extensive (si l'on double la quantité de chacun des réactifs et produits, l'avancement de réaction double également). Au début de la réaction, au moment de l'introduction des composants dans le réacteur, par définition l'avancement est nul :
permet de connaître la composition du système : c'est une variable de composition extensive (si l'on double la quantité de chacun des réactifs et produits, l'avancement de réaction double également). Au début de la réaction, au moment de l'introduction des composants dans le réacteur, par définition l'avancement est nul : 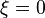 . Puis la valeur de l'avancement évolue selon le sens de déplacement de la réaction.
. Puis la valeur de l'avancement évolue selon le sens de déplacement de la réaction.
Lorsque la réaction progresse :
- les réactifs i disparaissent :
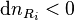 ;
; - les produits j apparaissent :
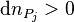 ;
; - l'état d'avancement augmente :
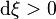 ;
; - la réaction directe l'emporte sur la réaction inverse :
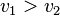 et
et 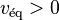 ;
; - l'équilibre se déplace de la gauche vers la droite.
À l'inverse, lorsque la réaction régresse :
- les réactifs i apparaissent :
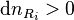 ;
; - les produits j disparaissent :
 ;
; - l'état d'avancement diminue :
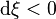 ;
; - la réaction directe est dominée par la réaction inverse :
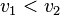 et
et 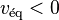 ;
; - l'équilibre se déplace de la droite vers la gauche.
L'avancement de réaction peut donc indifféremment augmenter ou diminuer. Puisque l'avancement est nul au début de la réaction, il peut prendre aussi bien une valeur positive 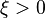 (la réaction a progressé par rapport à l'état initial) qu'une valeur négative
(la réaction a progressé par rapport à l'état initial) qu'une valeur négative 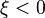 (la réaction a régressé par rapport à l'état initial). La vitesse de déplacement de l'équilibre est égale à la dérivée de l'avancement de la réaction par rapport au temps :
(la réaction a régressé par rapport à l'état initial). La vitesse de déplacement de l'équilibre est égale à la dérivée de l'avancement de la réaction par rapport au temps :
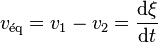
avec, à l'équilibre, 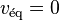 .
.
La convention stœchiométrique communément admise afin de simplifier les expressions dans les démonstrations qui suivent est de représenter l'équilibre sous la forme :
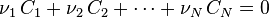
Cette équation (2) implique les mêmes constituants 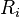 et
et  que l'expression de l'équilibre (1), mais ils sont cette fois notés
que l'expression de l'équilibre (1), mais ils sont cette fois notés 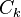 , au nombre de
, au nombre de 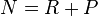 , en attribuant une valeur négative aux coefficients stœchiométriques des réactifs, et positive à ceux des produits :
, en attribuant une valeur négative aux coefficients stœchiométriques des réactifs, et positive à ceux des produits :
-
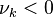 pour un réactif ;
pour un réactif ; -
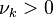 pour un produit.
pour un produit.
Exemple - La réaction de synthèse de l'urée :
- sera réécrite :
Ceci permet d'écrire indifféremment pour un réactif ou un produit :
Avancement de la réaction : 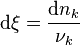 pour tout pour tout ![k \in [1,\cdots,N]](../i/m/c864e65009570b920ae9af63f9f5dbe2.png) |
À tout instant au cours de la réaction, l'intégration de ces relations permet de calculer la quantité d'un réactif ou d'un produit quelconque, selon :
avec :
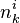 , la quantité de constituant à l'instant initial t = 0 ;
, la quantité de constituant à l'instant initial t = 0 ;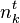 , la quantité de constituant à l'instant t ;
, la quantité de constituant à l'instant t ;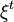 , l'avancement de réaction à l'instant t ; rappelons qu'à l'instant initial, par définition,
, l'avancement de réaction à l'instant t ; rappelons qu'à l'instant initial, par définition, 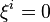 .
.
Pour un inerte, constituant n'intervenant pas dans la réaction, la quantité ne varie pas au cours de la réaction : pour un inerte on pourra écrire 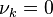 et
et 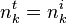 à tout instant.
à tout instant.
Critère d'évolution spontanée d'une réaction chimique et condition d'équilibre
Un système fermé est à l'équilibre lorsque les variables intensives qui le décrivent (température, pression et potentiels chimiques des réactifs et des produits) sont homogènes dans tout le système et restent constantes au cours du temps.
Le deuxième principe de la thermodynamique implique que pour une réaction chimique effectuée à P et T constantes la fonction enthalpie libre  ne peut que décroître. Donc sa variation doit être négative :
ne peut que décroître. Donc sa variation doit être négative :
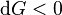
Lorsque  ne varie plus,
ne varie plus, 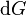 est nulle[12], la fonction
est nulle[12], la fonction  est minimale. Cela signifie que le système réactionnel est à l'équilibre :
est minimale. Cela signifie que le système réactionnel est à l'équilibre :
À l'équilibre : 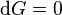 |
Le deuxième principe de la thermodynamique implique que pour une réaction chimique effectuée à V et T constants la fonction énergie libre 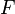 ne peut que décroître. Donc sa variation doit être négative :
ne peut que décroître. Donc sa variation doit être négative :
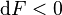
Lorsque 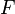 ne varie plus,
ne varie plus, 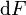 est nulle, la fonction
est nulle, la fonction 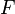 est minimale. Cela signifie que le système réactionnel est à l'équilibre :
est minimale. Cela signifie que le système réactionnel est à l'équilibre :
À l'équilibre : 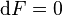 |
Les deux relations sont équivalentes, puisque 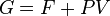 et qu'à l'équilibre la pression et le volume sont constants dans le temps. Dès lors à l'équilibre les deux grandeurs
et qu'à l'équilibre la pression et le volume sont constants dans le temps. Dès lors à l'équilibre les deux grandeurs  et
et 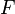 ne varient plus. On étudiera cependant les variations de la première pour les réactions ayant lieu à P et T constantes, et de la seconde pour les réactions ayant lieu à V et T constants.
ne varient plus. On étudiera cependant les variations de la première pour les réactions ayant lieu à P et T constantes, et de la seconde pour les réactions ayant lieu à V et T constants.
Réaction à pression et température constante
Les démonstrations qui suivent sont valables pour une réaction ayant lieu à P et T constantes, en se basant sur l'enthalpie libre  .
.
Définitions
Enthalpie libre de réaction
Soient 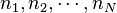 les quantités respectives des
les quantités respectives des 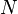 constituants de la réaction pour l'état
constituants de la réaction pour l'état 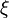 et
et 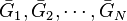 les enthalpies libres molaires partielles de chaque constituant à P et T données. L'enthalpie libre molaire partielle du constituant k, qui est également son potentiel chimique, est définie par :
les enthalpies libres molaires partielles de chaque constituant à P et T données. L'enthalpie libre molaire partielle du constituant k, qui est également son potentiel chimique, est définie par :
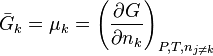 .
.
La différentielle de l'enthalpie libre est égale à :
Les relations liant l'évolution de l'avancement à l'évolution de chacun des constituants permettent d'écrire pour chaque constituant k :
On peut donc réécrire :
L'enthalpie libre de réaction est définie par :
avec 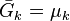 l'enthalpie libre molaire partielle ou potentiel chimique du constituant k.
l'enthalpie libre molaire partielle ou potentiel chimique du constituant k.
La différentielle de l'enthalpie libre est égale à :
d'où, à P et T constantes :
Cette grandeur est également notée avec l'opérateur de Lewis :
Pour résumer :
Enthalpie libre de réaction :  |
et :
À P et T constantes : 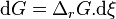 |
Quotient de réaction
Le potentiel chimique 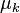 de chaque constituant k dans le mélange réactionnel peut être exprimé en fonction du potentiel chimique
de chaque constituant k dans le mélange réactionnel peut être exprimé en fonction du potentiel chimique  de ce constituant dans un état standard à la même température T que le mélange réactionnel et de l'activité
de ce constituant dans un état standard à la même température T que le mélange réactionnel et de l'activité 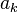 du constituant selon la relation :
du constituant selon la relation :
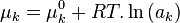
L'expression de l'enthalpie libre de réaction est développée selon :
Les termes standards  sont regroupés dans une grandeur appelée enthalpie libre standard de réaction :
sont regroupés dans une grandeur appelée enthalpie libre standard de réaction :
Enthalpie libre standard de réaction : 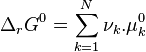 |
Les termes correspondant aux activités sont regroupés dans le quotient de réaction :
Quotient de réaction : 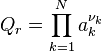 |
Pour résumer :
Enthalpie libre de réaction : 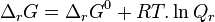 |
Constante d'équilibre
La constante d'équilibre 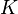 , qui est toujours positive, est définie par la relation avec l'enthalpie standard de réaction :
, qui est toujours positive, est définie par la relation avec l'enthalpie standard de réaction :
Constante d'équilibre : 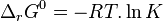 |
L'enthalpie libre standard de réaction est liée à l'enthalpie standard de réaction et à l'entropie standard de réaction par la relation :
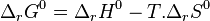
Lorsque 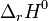 et
et 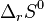 sont de même signe,
sont de même signe, 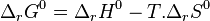 peut être négative (progression de la réaction favorisée
peut être négative (progression de la réaction favorisée 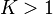 ) ou positive (régression favorisée
) ou positive (régression favorisée 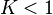 ) : la réaction produit un équilibre d'autant plus déplacé vers la droite (vers les produits) que
) : la réaction produit un équilibre d'autant plus déplacé vers la droite (vers les produits) que 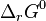 décroît et
décroît et 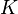 augmente. Nous retrouvons ici les principes de Berthelot et Matignon selon lesquels la réaction est favorisée si
augmente. Nous retrouvons ici les principes de Berthelot et Matignon selon lesquels la réaction est favorisée si 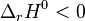 et
et 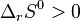 : si tel est le cas,
: si tel est le cas, 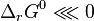 et
et 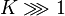 , la réaction est totale. A contrario, la réaction est impossible si
, la réaction est totale. A contrario, la réaction est impossible si 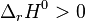 et
et  , auquel cas
, auquel cas 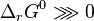 et
et  .
.
Il est supposé que l'enthalpie libre standard de réaction ne dépend que de la température ; rappelons que l'état standard est choisi à la même température T que le mélange réactionnel réel. Sur des plages de température réduites, l'enthalpie standard de réaction et l'entropie standard de réaction peuvent être considérées comme des constantes, selon l'approximation d'Ellingham. Aussi, en introduisant deux constantes  et
et 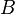 telles que :
telles que :
on obtient :
La constante 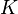 d'équilibre peut être trouvée dans la littérature pour de nombreux équilibres sous la forme :
d'équilibre peut être trouvée dans la littérature pour de nombreux équilibres sous la forme :
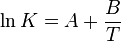
Cette expression est la plus courante, il est nécessaire de vérifier son domaine de validité en température qui est souvent assez réduit. Pour tenir compte de la variation des enthalpie et entropie standard de réaction, d'autres expressions peuvent être trouvées, permettant de travailler sur des plages de température plus larges.
La constante d'équilibre peut être calculée à l'aide des relations de Kirchhoff : il est important de noter que la constante d'équilibre peut être calculée à partir des seules propriétés des réactifs et produits à l'état standard[13],[14], propriétés qui sont supposées ne dépendre que de la température :
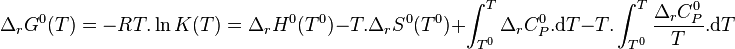
avec :
-
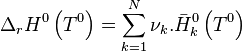 , l'enthalpie standard de réaction à
, l'enthalpie standard de réaction à 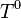 ;
; -
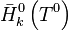 , l'enthalpie molaire standard du constituant k à
, l'enthalpie molaire standard du constituant k à 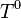 ;
; -
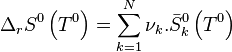 , l'entropie standard de réaction à
, l'entropie standard de réaction à 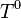 ;
; -
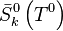 , l'entropie molaire standard du constituant k à
, l'entropie molaire standard du constituant k à 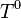 ;
; -
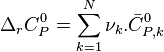 , la capacité thermique isobare standard de réaction, dépendante de T ;
, la capacité thermique isobare standard de réaction, dépendante de T ; -
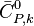 , la capacité thermique isobare molaire standard du constituant k, dépendante de T ;
, la capacité thermique isobare molaire standard du constituant k, dépendante de T ; -
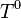 , température de référence.
, température de référence.
La constante d'équilibre peut bien sûr être également déterminée expérimentalement.
On a donc, finalement :
Pour résumer :
Enthalpie libre de réaction : 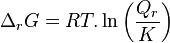 |
Enthalpie libre de réaction et équilibre
Sens de déplacement d'un équilibre, condition d'équilibre

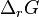 . La réaction progresse lorsque
. La réaction progresse lorsque 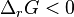 . La réaction régresse lorsque
. La réaction régresse lorsque  . L'équilibre est atteint lorsque
. L'équilibre est atteint lorsque 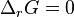 .
.Étant donné que, à pression P et température T constantes, la condition d'évolution spontanée est donnée par : 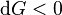 et que par définition de l'enthalpie libre de réaction :
et que par définition de l'enthalpie libre de réaction : 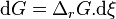 , alors
, alors 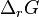 et
et 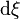 ne peuvent être que de signes contraires :
ne peuvent être que de signes contraires :
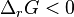 et
et 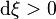 , la réaction progresse : l'équilibre se déplace de la gauche vers la droite, des réactifs sont consommés et des produits apparaissent ;
, la réaction progresse : l'équilibre se déplace de la gauche vers la droite, des réactifs sont consommés et des produits apparaissent ; et
et 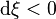 , la réaction régresse : l'équilibre se déplace de la droite vers la gauche, des produits sont consommés et des réactifs apparaissent.
, la réaction régresse : l'équilibre se déplace de la droite vers la gauche, des produits sont consommés et des réactifs apparaissent.
À l'équilibre 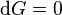 [12], d'où deux cas possibles :
[12], d'où deux cas possibles :
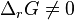 et
et 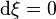 , la réaction pourrait avoir lieu car le potentiel de réaction est non nul, mais l'avancement de réaction ne varie pas ; les causes de ce défaut de réaction peuvent être :
, la réaction pourrait avoir lieu car le potentiel de réaction est non nul, mais l'avancement de réaction ne varie pas ; les causes de ce défaut de réaction peuvent être :
- une cinétique extrêmement lente (la vitesse de réaction
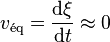 ; l'équilibre est dit instable),
; l'équilibre est dit instable), - ou l'absence d'un facteur déclenchant (apport d'énergie, étincelle, catalyseur, site de nucléation, ... ; l'équilibre est dit métastable)[15] ;
- une cinétique extrêmement lente (la vitesse de réaction
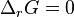 et
et  , la réaction a eu lieu, le potentiel de réaction est désormais nul ; l'équilibre est dit stable ou labile (termes équivalents) ; nous ne nous intéresserons par la suite qu'à ce cas de figure.
, la réaction a eu lieu, le potentiel de réaction est désormais nul ; l'équilibre est dit stable ou labile (termes équivalents) ; nous ne nous intéresserons par la suite qu'à ce cas de figure.
Dans un équilibre labile : 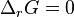 |
Il est à noter que l'enthalpie libre de réaction étant liée aux enthalpie et entropie de réaction par la relation 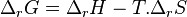 , l'état d'équilibre labile correspond à l'égalité
, l'état d'équilibre labile correspond à l'égalité 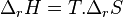 , soit l'équilibre entre le facteur énergie et le facteur désordre.
, soit l'équilibre entre le facteur énergie et le facteur désordre.
L'affinité chimique, notée 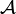 , est définie par l'opposé de l'enthalpie libre de réaction :
, est définie par l'opposé de l'enthalpie libre de réaction :
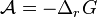
Le critère d'évolution spontanée de la réaction 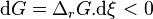 devient avec l'affinité chimique :
devient avec l'affinité chimique :
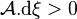
Elle permet une compréhension plus intuitive de l'évolution de la réaction, 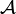 et
et 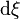 étant de même signe :
étant de même signe :
- une progression est associée à un signe positif :
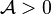 et
et 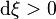 , la réaction progresse ;
, la réaction progresse ; - une régression est associée à un signe négatif :
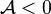 et
et 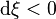 , la réaction régresse ;
, la réaction régresse ;
et bien entendu à l'équilibre :
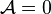
Loi d'action de masse
En considérant la condition d'évolution spontanée à pression et température constante : 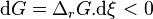 et la relation :
et la relation : 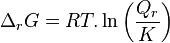 , hors équilibre nous avons :
, hors équilibre nous avons :
- si
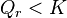 alors
alors 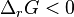 , d'où
, d'où 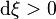 : la réaction progresse ;
: la réaction progresse ; - si
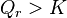 alors
alors  , d'où
, d'où 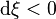 : la réaction régresse.
: la réaction régresse.
Lorsque la fonction  est minimale, le système réactionnel est à l'équilibre. Dans ces conditions :
est minimale, le système réactionnel est à l'équilibre. Dans ces conditions :
soit, à l'équilibre :
En notant 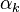 l'activité du constituant k à l'équilibre, le quotient de réaction à l'équilibre valant :
l'activité du constituant k à l'équilibre, le quotient de réaction à l'équilibre valant :
nous obtenons la loi d'action de masse :
Loi d'action de masse : 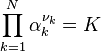 |
Pour calculer la composition du mélange réactionnel à l'équilibre, il faut donc résoudre l'équation 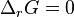 , soit
, soit 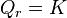 . Les activités chimiques qui interviennent dans le quotient de réaction dépendent de la pression P, de la température T et de la composition du mélange réactionnel, c'est-à-dire des quantités des réactifs et produits de réaction, mais aussi des inertes, les constituants n'intervenant pas dans la réaction :
. Les activités chimiques qui interviennent dans le quotient de réaction dépendent de la pression P, de la température T et de la composition du mélange réactionnel, c'est-à-dire des quantités des réactifs et produits de réaction, mais aussi des inertes, les constituants n'intervenant pas dans la réaction : 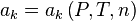 .
.
La pression P et la température T, ainsi que les quantités de réactifs, de produits et d'inertes dans le mélange réactionnel à l'instant initial (au temps t = 0) sont des données du problème. La réaction est menée à pression et température constantes. Pour un inerte, la quantité est constante au cours de la réaction. L'équation comporte donc autant d'inconnues qu'il y a de réactifs et de produits : il s'agit des N quantités de ces constituants, 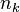 pour
pour ![k \in \left[1, \cdots , N \right]](../i/m/c095754b46e755e5b3e61d9efac3872b.png) , qui évoluent au cours de la réaction. Pour tout constituant k intervenant dans la réaction, la quantité varie au cours du temps selon :
, qui évoluent au cours de la réaction. Pour tout constituant k intervenant dans la réaction, la quantité varie au cours du temps selon :
avec :
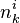 , la quantité du constituant k à l'instant initial t = 0 ;
, la quantité du constituant k à l'instant initial t = 0 ;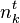 , la quantité du constituant k à l'instant t ;
, la quantité du constituant k à l'instant t ;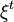 , l'avancement de réaction à l'instant t ; rappelons qu'à l'instant initial, par définition,
, l'avancement de réaction à l'instant t ; rappelons qu'à l'instant initial, par définition, 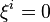 .
.
On peut donc remplacer dans l'expression des activités les 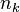 par
par 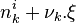 . Les pression, température et composition initiale étant données, le quotient de réaction
. Les pression, température et composition initiale étant données, le quotient de réaction 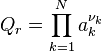 devient alors à tout instant (y compris hors équilibre) une fonction d'une seule variable : l'avancement de réaction
devient alors à tout instant (y compris hors équilibre) une fonction d'une seule variable : l'avancement de réaction 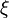 . Pour calculer la composition à l'équilibre, il faut donc trouver
. Pour calculer la composition à l'équilibre, il faut donc trouver 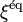 tel que :
tel que : 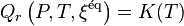 . La quantité de chaque réactif et produit à l'équilibre est a posteriori calculée par
. La quantité de chaque réactif et produit à l'équilibre est a posteriori calculée par 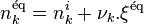 .
.
L'équation n'a pas forcément une solution unique en 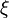 . Il est entendu que sont écartées d'office les solutions mathématiques induisant des quantités
. Il est entendu que sont écartées d'office les solutions mathématiques induisant des quantités 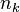 de constituants négatives (rappelons toutefois que l'avancement de réaction
de constituants négatives (rappelons toutefois que l'avancement de réaction 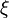 , lui, peut être négatif). Si plusieurs solutions sont trouvées, il est nécessaire de déterminer laquelle est la bonne, ou du moins laquelle est la plus réaliste du point de vue de la thermodynamique : celle qui minimise la fonction
, lui, peut être négatif). Si plusieurs solutions sont trouvées, il est nécessaire de déterminer laquelle est la bonne, ou du moins laquelle est la plus réaliste du point de vue de la thermodynamique : celle qui minimise la fonction  .
.
Pour résumer :
À l'équilibre : 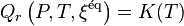 |
Condition de stabilité d'un équilibre

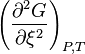 . L'équilibre n'est stable que lorsque
. L'équilibre n'est stable que lorsque 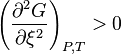 . De plus l'équilibre réel est celui pour lequel l'enthalpie libre
. De plus l'équilibre réel est celui pour lequel l'enthalpie libre  a atteint le minimum global sur l'ensemble des valeurs possibles de l'avancement de réaction
a atteint le minimum global sur l'ensemble des valeurs possibles de l'avancement de réaction 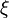 .
.D'un point de vue mathématique, un minimum de  est atteint si, en plus de l'annulation de sa dérivée première, sa dérivée seconde est positive strictement, soit, à l'équilibre :
est atteint si, en plus de l'annulation de sa dérivée première, sa dérivée seconde est positive strictement, soit, à l'équilibre :
À l'équilibre :  |
C'est à cette seconde condition seulement que l'équilibre pourra être qualifié de stable.
Il est impossible que 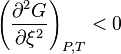 à l'équilibre, ce qui supposerait un maximum de la fonction
à l'équilibre, ce qui supposerait un maximum de la fonction  , et donc que
, et donc que  a crû. Si cette solution est mathématiquement possible, elle est irréaliste du point de vue de la thermodynamique et doit donc être écartée ; mathématiquement, il s'agit d'un équilibre instable. Il est possible en revanche qu'à l'équilibre
a crû. Si cette solution est mathématiquement possible, elle est irréaliste du point de vue de la thermodynamique et doit donc être écartée ; mathématiquement, il s'agit d'un équilibre instable. Il est possible en revanche qu'à l'équilibre  , c'est-à-dire que l'équilibre ait atteint un point d'inflexion de l'enthalpie libre : dans ce cas l'équilibre atteint est un équilibre métastable, et la moindre perturbation relancera la réaction jusqu'à ce qu'elle atteigne un équilibre stable. La situation est possible du point de vue de la thermodynamique. Il est nécessaire aussi de vérifier que le minimum atteint n'est pas un minimum local, c'est-à-dire un minimum auquel la réaction revient si elle subit de petites perturbations, mais dont la réaction s'éloigne définitivement sous des perturbations plus importantes, conduisant à un autre minimum de
, c'est-à-dire que l'équilibre ait atteint un point d'inflexion de l'enthalpie libre : dans ce cas l'équilibre atteint est un équilibre métastable, et la moindre perturbation relancera la réaction jusqu'à ce qu'elle atteigne un équilibre stable. La situation est possible du point de vue de la thermodynamique. Il est nécessaire aussi de vérifier que le minimum atteint n'est pas un minimum local, c'est-à-dire un minimum auquel la réaction revient si elle subit de petites perturbations, mais dont la réaction s'éloigne définitivement sous des perturbations plus importantes, conduisant à un autre minimum de  , plus bas. L'équilibre chimique à un minimum local de
, plus bas. L'équilibre chimique à un minimum local de  est un équilibre stable, néanmoins il ne s'agit pas de celui dans lequel l'enthalpie libre est minimale dans les conditions de la réaction. L'équilibre chimique réel est celui pour lequel l'enthalpie libre
est un équilibre stable, néanmoins il ne s'agit pas de celui dans lequel l'enthalpie libre est minimale dans les conditions de la réaction. L'équilibre chimique réel est celui pour lequel l'enthalpie libre  atteint le minimum global sur l'ensemble des valeurs possibles de l'avancement de réaction
atteint le minimum global sur l'ensemble des valeurs possibles de l'avancement de réaction 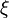 .
.
Les situations d'équilibre métastable ou de minimum local ne sont que rarement observées expérimentalement, mais elles peuvent être obtenues lors de simulations numériques d'équilibres. Les dérivées première et seconde de  ainsi que la possibilité d'un minimum local doivent être impérativement vérifiées pour garantir le résultat. Insistons également sur le fait que les modèles d'activité chimique ou les équations d'état utilisés dans les calculs thermodynamiques restent basés sur un certain nombre d'hypothèses pouvant conduire à des résultats numériquement corrects, mais néanmoins totalement irréalistes, surtout lorsque ces modèles sont employés en dehors de leur domaine de validité.
ainsi que la possibilité d'un minimum local doivent être impérativement vérifiées pour garantir le résultat. Insistons également sur le fait que les modèles d'activité chimique ou les équations d'état utilisés dans les calculs thermodynamiques restent basés sur un certain nombre d'hypothèses pouvant conduire à des résultats numériquement corrects, mais néanmoins totalement irréalistes, surtout lorsque ces modèles sont employés en dehors de leur domaine de validité.
Pour vérifier la condition de stabilité, on remarquera que :
Or la constante d'équilibre 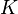 ne dépend que de la température, d'où :
ne dépend que de la température, d'où :
Le quotient de réaction 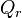 est toujours positif par définition. Pour vérifier que
est toujours positif par définition. Pour vérifier que 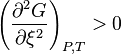 à l'équilibre, il faut donc vérifier que :
à l'équilibre, il faut donc vérifier que :
Condition de stabilité de l'équilibre : 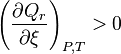 |
Loi d'Arrhenius
Reprenons la convention d'écriture d'un équilibre chimique dans laquelle les coefficients stœchiométriques sont tous positifs :
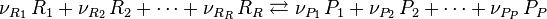
On écrit, si les deux réactions sont des réactions élémentaires :
- la vitesse de la réaction directe :
 ;
; - la vitesse de la réaction inverse :
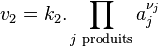 ;
;
avec :
-
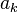 , l'activité du constituant k ;
, l'activité du constituant k ; -
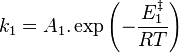 , constante de vitesse de la réaction directe exprimée selon la loi d'Arrhenius ;
, constante de vitesse de la réaction directe exprimée selon la loi d'Arrhenius ; -
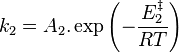 , constante de vitesse de la réaction inverse ;
, constante de vitesse de la réaction inverse ; -
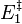 et
et 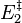 étant les énergies d'activation respectives ;
étant les énergies d'activation respectives ; -
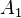 et
et 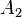 étant des constantes.
étant des constantes.
À l'équilibre, l'égalité des vitesses des deux réactions 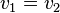 , en notant
, en notant 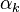 l'activité du constituant k à l'équilibre, conduit à :
l'activité du constituant k à l'équilibre, conduit à :
Nous retrouvons ainsi le quotient de réaction à l'équilibre, noté selon la convention stœchiométrique avec les coefficients de stœchiométrie des réactifs négatifs :
Nous pouvons en conséquence à l'équilibre écrire, en considérant la loi d'action de masse établie précédemment :
d'où les relations entre loi d'Arrhenius, constante d'équilibre et enthalpie libre standard de réaction :
soit donc pour des réactions élémentaires[16],[17],[18] :
Enthalpie standard de réaction : 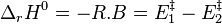 |
Entropie standard de réaction : 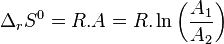 |
Résumé
De façon générale, à l'équilibre et hors équilibre :
- à P et T constantes, l'évolution spontanée de la réaction est dictée par le second principe de la thermodynamique :
- enthalpie libre de réaction :
- potentiels chimiques :
- enthalpie libre standard de réaction, potentiels chimiques à l'état standard et constante d'équilibre :
- quotient de réaction et activités :
Avec les relations :
Il est important de noter que l'enthalpie libre standard de réaction 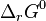 , liée à la constante d'équilibre
, liée à la constante d'équilibre 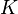 , ne permet que de définir l'équilibre du système réactionnel. Pour étudier le système réactionnel hors équilibre, il faut étudier l'enthalpie libre de réaction
, ne permet que de définir l'équilibre du système réactionnel. Pour étudier le système réactionnel hors équilibre, il faut étudier l'enthalpie libre de réaction 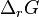 . En effet, hors équilibre nous avons :
. En effet, hors équilibre nous avons :
- si
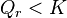 , alors
, alors 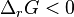 et
et 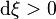 : la réaction progresse ;
: la réaction progresse ; - si
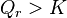 , alors
, alors  et
et 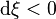 : la réaction régresse.
: la réaction régresse.
À l'équilibre : 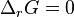 , soit , soit 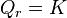 |
La constante d'équilibre 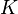 peut être :
peut être :
- calculée à partir des propriétés des réactifs et des produits dans leur état standard ;
- calculée à l'aide des paramètres de la loi d'Arrhenius des constantes dans l'expression des vitesses des réactions directe et inverse ;
- déterminée expérimentalement ;
- trouvée dans la littérature pour de nombreux équilibres.
Lors d'un calcul d'équilibre, il convient également de vérifier que la solution obtenue correspond bien à un minimum de la fonction  selon la condition de stabilité :
selon la condition de stabilité :
Condition de stabilité de l'équilibre : 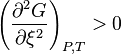 , soit , soit 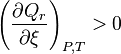 |
Déplacement d'un équilibre chimique
Principe de modération de Le Chatelier
« Principe de modération de Le Chatelier
Lorsque les modifications extérieures apportées à un système physico-chimique en équilibre provoquent une évolution vers un nouvel état d'équilibre, l'évolution s'oppose aux perturbations qui l'ont engendrée et en modère l'effet. »
Pour un système fermé ce principe est toujours vrai et sera démontré dans les deux cas suivants :
- déplacement de l'équilibre par modification de la température ;
- déplacement de l'équilibre par modification de la pression.
Le principe de modération de Le Chatelier est souvent observé dans le déplacement de l'équilibre par modification de la composition (ajout ou extraction d'un réactif, d'un produit ou d'un inerte, le système étant alors un système ouvert), néanmoins il existe des cas dans lesquels il n'est pas respecté, ce qui sera démontré pour une solution idéale.
Déplacement par modification de la température
Relation de van 't Hoff
L'enthalpie libre standard de réaction s'exprime en fonction de l'enthalpie standard de réaction et de l'entropie standard de réaction selon :
La relation de Gibbs-Helmholtz permettant d'écrire, à pression constante :
on obtient la relation de van 't Hoff qui définit l'évolution de la constante d'équilibre 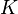 d'un équilibre chimique (supposée ne dépendre que de T), en fonction de la température :
d'un équilibre chimique (supposée ne dépendre que de T), en fonction de la température :
Relation de van 't Hoff : 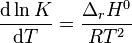 |
En intégrant cette relation, en supposant que l'enthalpie standard de réaction ne varie pas avec la température, on obtient :
Si l'on connait la valeur de la constante d'équilibre, 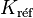 , à la température
, à la température 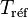 , il est possible de déterminer la nouvelle valeur de la constante d'équilibre
, il est possible de déterminer la nouvelle valeur de la constante d'équilibre 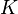 à la température T.
à la température T.
Déplacement d'équilibre, loi de van 't Hoff
Supposons un équilibre à P et T1. La température est modifiée à T2, l'équilibre se déplace et se stabilise T2, la pression P restant constante. La constante d'équilibre change, passant de  à
à 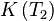 .
.
La relation de Gibbs-Helmholtz permet d'écrire, à pression et composition constantes :
En intégrant de 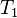 à
à 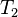 , à pression
, à pression  et composition de l'équilibre initial constantes et en considérant que l'enthalpie de réaction est constante sur l'intervalle de température, nous obtenons :
et composition de l'équilibre initial constantes et en considérant que l'enthalpie de réaction est constante sur l'intervalle de température, nous obtenons :
Or à l'équilibre initial :
d'où :
Avant déplacement de l'équilibre :
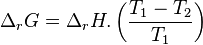 |
Il vient cinq cas de figure :
-
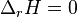 , l'enthalpie de réaction est nulle, la réaction est insensible à la température,
, l'enthalpie de réaction est nulle, la réaction est insensible à la température, -
 , la réaction est exothermique, l'équilibre dégage de la chaleur en se déplaçant de la gauche vers la droite :
, la réaction est exothermique, l'équilibre dégage de la chaleur en se déplaçant de la gauche vers la droite :
- on augmente la température
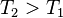 :
: 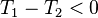 , d'où
, d'où  , en augmentant la température d'une réaction exothermique la réaction régresse,
, en augmentant la température d'une réaction exothermique la réaction régresse, - on diminue la température
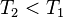 :
: 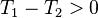 , d'où
, d'où 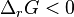 , en diminuant la température d'une réaction exothermique, la réaction progresse,
, en diminuant la température d'une réaction exothermique, la réaction progresse,
- on augmente la température
-
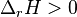 , la réaction est endothermique l'équilibre absorbe de la chaleur en se déplaçant de la gauche vers la droite :
, la réaction est endothermique l'équilibre absorbe de la chaleur en se déplaçant de la gauche vers la droite :
- on augmente la température
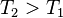 :
: 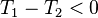 , d'où
, d'où 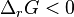 , en augmentant la température d'une réaction endothermique, la réaction progresse,
, en augmentant la température d'une réaction endothermique, la réaction progresse, - on diminue la température
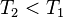 :
: 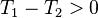 , d'où
, d'où  , en diminuant la température d'une réaction endothermique, la réaction régresse.
, en diminuant la température d'une réaction endothermique, la réaction régresse.
- on augmente la température
Ces relations sont résumées par la loi de van 't Hoff, qui la découvrit expérimentalement :
| Loi de van 't Hoff : une augmentation de température à pression constante déplace l'équilibre dans le sens qui s'oppose à cette augmentation, le sens endothermique. | Inversement, une diminution de température à pression constante déplace l'équilibre dans le sens qui s'oppose à cette diminution, le sens exothermique. |
Exemple - Équilibre monomère-dimère du dioxyde d'azote
- Le monomère dioxyde d'azote NO2 et son dimère le peroxyde d'azote N2O4 sont en équilibre permanent selon la réaction :
- La chaleur de réaction est de
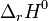 (298,15 K) = –57,23 kJ/mol, la réaction est donc exothermique. À basse température, le dimère est l'espèce prépondérante, à haute température c'est le monomère.
(298,15 K) = –57,23 kJ/mol, la réaction est donc exothermique. À basse température, le dimère est l'espèce prépondérante, à haute température c'est le monomère.
- Nous vérifions d'autre part que la progression de la réaction est favorisée selon le principe de Berthelot (réaction exothermique), et que la régression de la réaction est favorisée selon le principe de Matignon (augmentation de la quantité de constituants). Les deux réactions sont donc antagonistes d'où l'existence de l'équilibre.
Déplacement par modification de la pression
Cas général
Supposons un équilibre à P1 et T. La pression est modifiée à P2, l'équilibre se déplace et se stabilise à P2, la température T restant constante. La constante d'équilibre 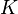 ne change pas, puisqu'elle ne dépend que de la température. Ce sont les activités des réactifs et produits dans le quotient de réaction
ne change pas, puisqu'elle ne dépend que de la température. Ce sont les activités des réactifs et produits dans le quotient de réaction 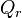 qui sont modifiées par le changement de pression.
qui sont modifiées par le changement de pression.
La variation isotherme du potentiel chimique en fonction de la pression est donnée par :
avec le volume molaire partiel du composant k :
En pondérant par les coefficients stœchiométriques, et en sommant sur l'ensemble des réactifs et produits, nous obtenons :
En notant avec l'opérateur de Lewis le volume de réaction :
nous obtenons :
L'intégration par rapport à P, en considérant T et la composition constantes, donne :
or à P1 et T, à la composition de l'équilibre initial :
donc avant le déplacement de l'équilibre par changement de la pression :
Avant déplacement de l'équilibre :
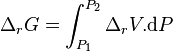 |
Cas des gaz parfaits, loi de Le Chatelier
Pour les gaz parfaits, le volume molaire partiel de chacun des constituants vaut :
D'où :
Pour les gaz parfaits, avant déplacement de l'équilibre :
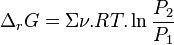 |
avec 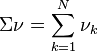 .
.
Il vient cinq cas de figure :
-
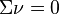 , si la somme des coefficients stœchiométriques est nulle, la réaction est insensible à un changement de pression,
, si la somme des coefficients stœchiométriques est nulle, la réaction est insensible à un changement de pression, -
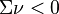 , la quantité totale de constituants (réactifs et produits) diminue lorsque l'équilibre se déplace de la gauche vers la droite :
, la quantité totale de constituants (réactifs et produits) diminue lorsque l'équilibre se déplace de la gauche vers la droite :
- on augmente la pression
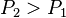 :
: 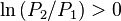 , d'où
, d'où 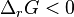 , en augmentant la pression la réaction progresse,
, en augmentant la pression la réaction progresse, - on diminue la pression
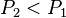 :
: 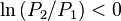 , d'où
, d'où  , en diminuant la pression la réaction régresse,
, en diminuant la pression la réaction régresse,
- on augmente la pression
-
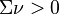 , la quantité totale de constituants (réactifs et produits) augmente lorsque l'équilibre se déplace de la gauche vers la droite :
, la quantité totale de constituants (réactifs et produits) augmente lorsque l'équilibre se déplace de la gauche vers la droite :
- on augmente la pression
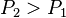 :
: 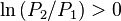 , d'où
, d'où  , en augmentant la pression la réaction régresse,
, en augmentant la pression la réaction régresse, - on diminue la pression
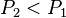 :
: 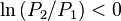 , d'où
, d'où 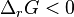 , en diminuant la pression la réaction progresse.
, en diminuant la pression la réaction progresse.
- on augmente la pression
Ces relations sont résumées par la loi de Le Chatelier, qui la découvrit expérimentalement :
| Loi de Le Chatelier : une augmentation de pression à température constante déplace l'équilibre dans le sens qui s'oppose à cette augmentation, celui qui diminue la quantité totale de constituants (réactifs et produits) dans le mélange. | Inversement, une diminution de pression à température constante déplace l'équilibre dans le sens qui s'oppose à cette diminution, celui qui augmente la quantité totale de constituants (réactifs et produits) dans le mélange. |
Exemple 1 - Synthèse de l'iodure d'hydrogène
- La réaction de synthèse de l'iodure d'hydrogène à partir d'hydrogène et d'iode s'écrit :
- La somme des coefficients stœchiométriques est donc de
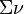 = –1–1+2 = 0. Cette réaction est insensible aux changements de pression.
= –1–1+2 = 0. Cette réaction est insensible aux changements de pression.
Exemple 2 - Synthèse de l'ammoniac
- Dans le procédé Haber-Bosch, la synthèse de l'ammoniac est effectuée selon la réaction :
- La somme des coefficients stœchiométriques est donc de
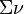 = –1–3+2 = –2. La synthèse de l'ammoniac est donc effectuée à haute pression entre 150 et 250 bar.
= –1–3+2 = –2. La synthèse de l'ammoniac est donc effectuée à haute pression entre 150 et 250 bar.
Cas des liquides et des solides
Pour les liquides ou les solides, le volume molaire partiel 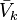 peut être considéré comme indépendant de la pression. En conséquence :
peut être considéré comme indépendant de la pression. En conséquence :
Pour les liquides et les solides, avant déplacement de l'équilibre :
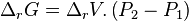 |
Il vient cinq cas de figure :
-
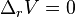 , si le volume de réaction est nul, la réaction est insensible à un changement de pression,
, si le volume de réaction est nul, la réaction est insensible à un changement de pression, -
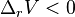 , le volume se contracte lorsque l'équilibre se déplace de la gauche vers la droite :
, le volume se contracte lorsque l'équilibre se déplace de la gauche vers la droite :
- on augmente la pression
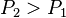 :
: 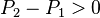 , d'où
, d'où 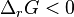 , en augmentant la pression la réaction progresse,
, en augmentant la pression la réaction progresse, - on diminue la pression
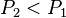 :
: 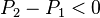 , d'où
, d'où  , en diminuant la pression la réaction régresse,
, en diminuant la pression la réaction régresse,
- on augmente la pression
-
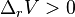 , le volume se dilate lorsque l'équilibre se déplace de la gauche vers la droite :
, le volume se dilate lorsque l'équilibre se déplace de la gauche vers la droite :
- on augmente la pression
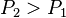 :
: 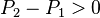 , d'où
, d'où  , en augmentant la pression la réaction régresse,
, en augmentant la pression la réaction régresse, - on diminue la pression
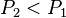 :
: 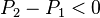 , d'où
, d'où 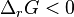 , en diminuant la pression la réaction progresse.
, en diminuant la pression la réaction progresse.
- on augmente la pression
Pour résumer :
| Une augmentation de pression à température constante déplace l'équilibre dans le sens dans lequel le volume se contracte. | Inversement, une diminution de pression à température constante déplace l'équilibre dans le sens dans lequel le volume se dilate. |
Exemple - Synthèse du diamant
- Le graphite et le diamant sont deux formes allotropiques du carbone en équilibre selon :
- Le volume molaire du diamant est de 3,4166 cm3/mol. Le volume molaire du graphite est de 5,2982 cm3/mol[19].
- Le volume de réaction est donc de
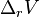 = –5,2982 + 3,4166 = –1,8816 cm3/mol, la synthèse du diamant est effectuée à haute pression : 58 000 atm. Revenu à basse pression, le diamant tend à redevenir graphite, mais la réaction est extrêmement lente, aussi parle-t-on d'équilibre instable.
= –5,2982 + 3,4166 = –1,8816 cm3/mol, la synthèse du diamant est effectuée à haute pression : 58 000 atm. Revenu à basse pression, le diamant tend à redevenir graphite, mais la réaction est extrêmement lente, aussi parle-t-on d'équilibre instable.
Déplacement par modification de la composition
À pression et température constantes, le principe de Le Chatelier n'est pas toujours observé dans les déplacements d'équilibre par ajout ou extraction de l'un des constituants du mélange réactionnel[20].
Le principe de modération voudrait que d'une façon générale l'ajout d'un réactif (ou l'extraction d'un produit) déplace l'équilibre dans le sens de la consommation du réactif (respectivement de l'apparition du produit), donc que la réaction progresse. A contrario, l'extraction d'un réactif ou l'ajout d'un produit devrait avoir pour conséquence une régression de la réaction.
Il n'en va pas toujours ainsi. Nous allons le démontrer dans le cas d'une solution idéale.
Il est à noter que, dans le cas présent, le principe de modération n'est pas respecté parce que l'une des conditions de l'équilibre n'est pas respectée : pour étudier un équilibre le système réactionnel doit être un système fermé, or l'ajout ou l'extraction d'un composant suppose un système ouvert.
Cas général
Supposons un équilibre à P et T. La quantité du constituant i (réactif, produit ou inerte) initialement de 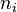 moles est modifiée à
moles est modifiée à 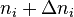 moles, l'équilibre se déplace et se stabilise, P et T restant constantes. La constante d'équilibre
moles, l'équilibre se déplace et se stabilise, P et T restant constantes. La constante d'équilibre 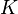 ne change pas, puisqu'elle ne dépend que de la température. Ce sont les activités des réactifs et produits dans le quotient de réaction
ne change pas, puisqu'elle ne dépend que de la température. Ce sont les activités des réactifs et produits dans le quotient de réaction 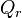 qui sont modifiées par le changement de composition.
qui sont modifiées par le changement de composition.
Dérivons l'enthalpie de réaction par rapport à 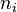 à pression, température et quantités des constituants autres que i constantes :
à pression, température et quantités des constituants autres que i constantes :
Le potentiel chimique de tout corps k dans la solution réelle s'exprime à partir du potentiel chimique de ce corps dans son état standard selon :
Pour une solution réelle, la modification de composition induit une modification de l'enthalpie libre de réaction telle que :
![\left( \frac{\partial \Delta_r G}{\partial n_i} \right) _{P,T,n_{j \neq i}}
= \left[ \sum_{k=1}^{N} \nu_k.\left( \frac{\partial \ln a_k}{\partial n_i} \right) _{P,T,n_{j \neq i}}\right].RT](../i/m/fcda0e582a1d1cea9d0280d276d0bf38.png) |
Cette expression ne peut pas être étudiée pour une solution réelle, car l'évolution des activités des solutions réelles est extrêmement complexe. Cette étude est cependant réalisable pour une solution idéale.
Cas d'une solution idéale
Dérivons l'enthalpie de réaction par rapport à 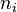 à pression, température et quantités des constituants autres que i constantes :
à pression, température et quantités des constituants autres que i constantes :
Selon la définition d'une solution idéale, le potentiel chimique de tout corps k dans la solution idéale s'exprime à partir du potentiel chimique de ce corps pur selon :
avec :
-
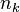 , la quantité de matière du constituant k (réactif, produit ou inerte) ;
, la quantité de matière du constituant k (réactif, produit ou inerte) ; -
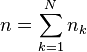 , la quantité de matière totale du mélange réactionnel (réactifs, produits et inertes) ;
, la quantité de matière totale du mélange réactionnel (réactifs, produits et inertes) ; -
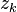 , fraction molaire du constituant k,
, fraction molaire du constituant k, 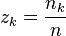 ;
; -
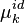 , potentiel chimique du constituant k dans la solution idéale ;
, potentiel chimique du constituant k dans la solution idéale ; -
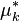 , potentiel chimique du constituant k pur, à mêmes P, T et phase que la solution idéale,
, potentiel chimique du constituant k pur, à mêmes P, T et phase que la solution idéale,
d'où la dérivée partielle du potentiel chimique dans le cas de la solution idéale :
Avec :
nous pouvons écrire pour la solution idéale :
En intégrant entre 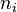 et
et 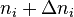 à P et T constantes, nous obtenons :
à P et T constantes, nous obtenons :
Pour une variation 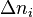 infiniment petite de
infiniment petite de 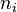 , nous pouvons écrire approximativement (par développement limité de la fonction logarithme naturel) :
, nous pouvons écrire approximativement (par développement limité de la fonction logarithme naturel) :
d'où :
Or à l'équilibre initial :
d'où :
Pour une solution idéale, avant déplacement de l'équilibre :
![\Delta_r G^{id} = \left[ \nu_i - z_i. \Sigma \nu \right] . \frac{\Delta n_i}{n_i}. RT](../i/m/29cce907de314e2836b36e4ed34cacfc.png) |
avec 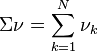 .
.
Déplacement par ajout ou extraction d'un réactif ou d'un produit
Il vient quatre cas de figure :
- si
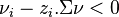 :
:
- si l'on ajoute le constituant i,
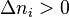 et
et 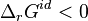 , en ajoutant le constituant i la réaction progresse,
, en ajoutant le constituant i la réaction progresse, - si l'on extrait le constituant i,
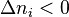 et
et 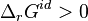 , en extrayant le constituant i la réaction régresse,
, en extrayant le constituant i la réaction régresse,
- si l'on ajoute le constituant i,
- si
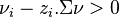 :
:
- si l'on ajoute le constituant i,
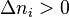 et
et 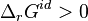 , en ajoutant le constituant i la réaction régresse,
, en ajoutant le constituant i la réaction régresse, - si l'on extrait le constituant i,
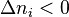 et
et 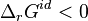 , en extrayant le constituant i la réaction progresse.
, en extrayant le constituant i la réaction progresse.
- si l'on ajoute le constituant i,
Si 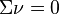 le principe de Le Chatelier est toujours respecté.
le principe de Le Chatelier est toujours respecté.
Si 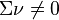 l'expression de l'enthalpie libre de réaction avant déplacement de l'équilibre dépend de la composition du mélange, alors :
l'expression de l'enthalpie libre de réaction avant déplacement de l'équilibre dépend de la composition du mélange, alors :
Pour tout constituant i (réactif ou produit) pour lequel 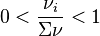 , le signe de l'enthalpie libre de réaction dépend du positionnement de
, le signe de l'enthalpie libre de réaction dépend du positionnement de 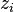 par rapport à
par rapport à 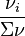 . En conséquence, selon la composition du mélange dans l'équilibre initial, l'ajout d'un constituant pourra déplacer l'équilibre dans un sens ou dans l'autre et le principe de Le Chatelier pourra ne pas être respecté. Par exemple, l'ajout d'un réactif pourra déplacer l'équilibre dans le sens de la régression de la réaction, et non de sa progression comme le voudrait le principe de modération.
. En conséquence, selon la composition du mélange dans l'équilibre initial, l'ajout d'un constituant pourra déplacer l'équilibre dans un sens ou dans l'autre et le principe de Le Chatelier pourra ne pas être respecté. Par exemple, l'ajout d'un réactif pourra déplacer l'équilibre dans le sens de la régression de la réaction, et non de sa progression comme le voudrait le principe de modération.
Exemple 1 - Synthèse de l'ammoniac
- Cet exemple donne un cas de violation du principe de modération[21].
- Reprenons la réaction de synthèse de l'ammoniac dans le procédé Haber-Bosch :
- La somme des coefficients stœchiométriques vaut :
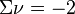 .
.
- Pour l'ammoniac, produit dont le coefficient stœchiométrique vaut :
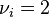 , nous avons
, nous avons 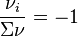 , quelle que soit la valeur de la fraction molaire initiale d'ammoniac
, quelle que soit la valeur de la fraction molaire initiale d'ammoniac 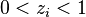 , nous avons
, nous avons 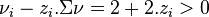 , d'où :
, d'où :
- en ajoutant de l'ammoniac, la réaction régresse,
- en extrayant de l'ammoniac, la réaction progresse,
- le principe de Le Chatelier est respecté.
- Pour l'hydrogène, réactif dont le coefficient stœchiométrique vaut :
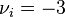 , nous avons
, nous avons 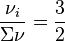 , quelle que soit la valeur de la fraction molaire initiale d'hydrogène
, quelle que soit la valeur de la fraction molaire initiale d'hydrogène 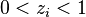 , nous avons
, nous avons 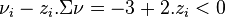 , d'où :
, d'où :
- en ajoutant de l'hydrogène, la réaction progresse,
- en extrayant de l'hydrogène, la réaction régresse,
- le principe de Le Chatelier est respecté.
- Pour l'azote, réactif dont le coefficient stœchiométrique vaut :
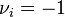 , nous avons
, nous avons 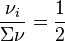 :
:
- si la fraction molaire initiale d'azote est
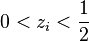 , alors
, alors 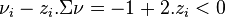 :
:
- en ajoutant de l'azote, la réaction progresse,
- en extrayant de l'azote, la réaction régresse,
- le principe de Le Chatelier est respecté.
- si la fraction molaire initiale d'azote est
 , alors
, alors 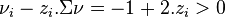 :
:
- en ajoutant de l'azote, la réaction régresse,
- en extrayant de l'azote, la réaction progresse,
- le principe de Le Chatelier n'est pas respecté !
- si la fraction molaire initiale d'azote est
Exemple 2 - Effet d'ion commun
- L'effet d'ion commun est un exemple d'application du principe de modération.
- La dissolution du chlorure de sodium (NaCl), ou sel de table, est donnée par la réaction :
- La solubilité du chlorure de sodium est donnée par le produit de solubilité :
- Si l'on ajoute un autre sel contenant un ion commun avec le chlorure de sodium, par exemple le sulfate de sodium, qui lui-même se dissout selon la réaction :
- on augmente la concentration des ions Na+. En conséquence, l'équilibre du chlorure de sodium se déplace dans le sens de la consommation de ce cation, c'est-à-dire de la précipitation du NaCl, de droite à gauche.
- De même, la dissolution de chlorure d'hydrogène HCl produit des ions Cl−, et donc augmente la concentration de cet anion : l'équilibre du chlorure de sodium se déplace dans le sens de la consommation de cet anion, de droite à gauche.
- Au contraire, si l'on ajoute de l'acide sulfurique H2SO4 à la solution saline, celui-ci se dissout en formant des ions SO42− qui font précipiter le sulfate de sodium Na2SO4 selon la réaction vue plus haut. La concentration en ion Na+ diminue, en conséquence l'équilibre du chlorure de sodium se déplace dans le sens de la production du cation, celui de la dissolution du sel, de gauche à droite.
Exemple 3 - Équilibre du calcaire et de la chaux
- Cet exemple montre qu'une réaction en équilibre peut devenir totale en application du principe de modération lorsque les conditions de l'équilibre ne sont pas respectées.
- Le calcaire CaCO3 et la chaux CaO sont en équilibre selon la réaction :
- Cet équilibre dépend de la pression du dioxyde de carbone. Si l'on supprime la condition de l'équilibre qui veut que la réaction se passe dans un milieu fermé, par exemple en ouvrant le réacteur à l'atmosphère, alors le CO2 s'échappe du milieu réactionnel au fur et à mesure de la réaction et ne peut jamais atteindre la pression d'équilibre. La réaction va en conséquence se déplacer dans le sens de la production du CO2 jusqu'à épuisement du calcaire : la réaction est totale, on dit qu'il y a rupture d'équilibre. Ceci est mis à profit dans les fours à chaux.
- La réaction inverse est utilisée dans les absorbeurs de CO2.
- Dans un four à chaux la réaction se produit en brûlant simultanément du coke ou du charbon, elle est donc endothermique. Nous vérifions ainsi que la régression de la réaction est favorisée selon le principe de Berthelot (réaction exothermique), et que la progression de la réaction est favorisée selon le principe de Matignon (augmentation de la quantité de constituants, création d'un gaz à partir d'un solide). Les deux réactions sont donc antagonistes, d'où l'existence de l'équilibre.
Déplacement par ajout ou extraction d'un inerte
Dans le cas de l'ajout d'un composant inerte, c'est-à-dire d'un constituant qui n'intervient pas dans la réaction, 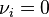 , à pression et température constantes :
, à pression et température constantes :
Il vient cinq cas de figure :
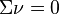 , si la somme des coefficients stœchiométriques est nulle, la réaction est insensible à l'ajout d'un inerte à P et T constantes,
, si la somme des coefficients stœchiométriques est nulle, la réaction est insensible à l'ajout d'un inerte à P et T constantes,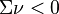 , le nombre total de constituants (réactifs et produits, hors inertes) diminue lorsque l'équilibre se déplace de la gauche vers la droite :
, le nombre total de constituants (réactifs et produits, hors inertes) diminue lorsque l'équilibre se déplace de la gauche vers la droite :
- on ajoute de l'inerte i,
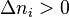 :
: 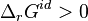 , en ajoutant un inerte la réaction régresse,
, en ajoutant un inerte la réaction régresse, - on extrait de l'inerte i,
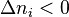 :
: 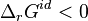 , en extrayant un inerte la réaction progresse,
, en extrayant un inerte la réaction progresse,
- on ajoute de l'inerte i,
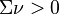 , le nombre total de constituants (réactifs et produits, hors inertes) augmente lorsque l'équilibre se déplace de la gauche vers la droite :
, le nombre total de constituants (réactifs et produits, hors inertes) augmente lorsque l'équilibre se déplace de la gauche vers la droite :
- on ajoute de l'inerte i,
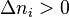 :
: 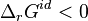 , en ajoutant un inerte, la réaction progresse,
, en ajoutant un inerte, la réaction progresse, - on extrait de l'inerte i,
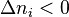 :
: 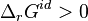 , en extrayant un inerte, la réaction régresse.
, en extrayant un inerte, la réaction régresse.
- on ajoute de l'inerte i,
| L'ajout d'un inerte à pression et température constantes déplace l'équilibre dans le sens qui augmente la quantité totale de constituants (réactifs et produits) dans le mélange. | Inversement, l'extraction d'un inerte à pression et température constantes déplace l'équilibre dans le sens qui diminue la quantité totale de constituants (réactifs et produits) dans le mélange. |
Ce résultat peut sembler paradoxal, on pourrait en effet s'attendre à ce que l'ajout d'un inerte déplace l'équilibre dans le sens d'une diminution de la quantité globale de réactifs et de produits, et non à une augmentation. Toutefois cette tendance est cohérente avec le principe de déplacement de l'équilibre par modification de la pression vu plus haut.
En effet, en supposant que le mélange réactionnel soit un mélange de gaz parfaits sans inertes, alors dans l'équilibre initial :
relation dans laquelle 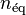 est la somme des quantités des réactifs et des produits.
est la somme des quantités des réactifs et des produits.
Si l'on ajoute à cet équilibre un inerte en conservant P et T constantes, cela suppose que le volume augmente, passant de 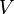 à
à 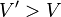 . Avant déplacement de l'équilibre nous avons une nouvelle relation :
. Avant déplacement de l'équilibre nous avons une nouvelle relation :
La pression due aux seuls réactifs et produits impliqués dans la réaction est donc passée de  à la pression partielle :
à la pression partielle :
Puisque 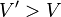 , alors
, alors 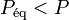 , autrement dit pour les réactifs et les produits la pression a diminué, et en application du principe de modération l'équilibre va se déplacer dans le sens d'une augmentation de la quantité globale de réactifs et de produits.
, autrement dit pour les réactifs et les produits la pression a diminué, et en application du principe de modération l'équilibre va se déplacer dans le sens d'une augmentation de la quantité globale de réactifs et de produits.
Par contre, si l'ajout d'inerte se fait à volume et température constants, alors après ajout de l'inerte la pression globale vaut :
La pression globale augmente donc, mais la pression partielle de l'équilibre reste inchangée :
L'équilibre ne va donc pas se déplacer. Il en va de même pour l'extraction d'un inerte.
| L'ajout ou l'extraction d'un inerte à volume et température constants n'a aucun effet sur l'équilibre. |
Exemple - Synthèse de l'ammoniac
- Reprenons la réaction de synthèse de l'ammoniac dans le procédé Haber-Bosch :
- La somme des coefficients stœchiométriques vaut :
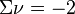 . Puisque cette somme est négative, l'ajout d'un inerte (par ex. de l'Argon) à pression et température constantes déplace l'équilibre dans le sens de la production d'azote et d'hydrogène. Pour un bon rendement de la réaction, il vaut mieux éviter l'introduction d'inertes dans le mélange réactionnel.
. Puisque cette somme est négative, l'ajout d'un inerte (par ex. de l'Argon) à pression et température constantes déplace l'équilibre dans le sens de la production d'azote et d'hydrogène. Pour un bon rendement de la réaction, il vaut mieux éviter l'introduction d'inertes dans le mélange réactionnel.
Emploi d'un catalyseur
Un catalyseur augmente la vitesse des réactions en abaissant leur énergie d'activation ; il permet donc d'atteindre plus vite l'équilibre.
Un catalyseur agit cependant de façon identique sur la réaction directe et la réaction inverse. Autrement dit, si l'énergie d'activation 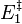 de la réaction directe varie de
de la réaction directe varie de 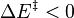 par l'effet du catalyseur, devenant
par l'effet du catalyseur, devenant 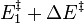 , alors l'énergie d'activation
, alors l'énergie d'activation 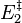 de la réaction inverse devient
de la réaction inverse devient  .
.
L'enthalpie standard de réaction (voir le paragraphe Loi d'Arrhenius) avant ajout du catalyseur :
n'est donc pas modifiée, puisqu'après ajout du catalyseur on a :
![\Delta_rH^0 = \left[ E_1^{\ddagger} +\Delta E^{\ddagger} \right] - \left[ E_2^{\ddagger} +\Delta E^{\ddagger} \right] = E_1^{\ddagger} - E_2^{\ddagger}](../i/m/9be979f6954210fda5cbb026210d91ae.png) .
.
L'entropie standard de réaction 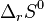 n'est pas modifiée par le catalyseur. L'enthalpie libre standard de réaction :
n'est pas modifiée par le catalyseur. L'enthalpie libre standard de réaction :
n'est donc globalement pas modifiée par l'ajout d'un catalyseur. Par conséquent la constante d'équilibre :
n'est pas modifiée par le catalyseur.
| Un catalyseur permet d'atteindre plus rapidement l'équilibre, mais il ne permet pas de le déplacer. |
Équilibres chimiques simultanés
Généralités
Soit un milieu réactionnel siège de M réactions simultanées impliquant N constituants 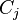 :
:
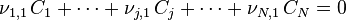
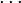
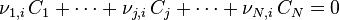
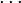
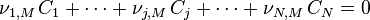
On note :
- i, l'indice des réactions,
![i \in \left[1, \cdots , M \right]](../i/m/624bce5eb67eeadea4896bf75700f5fd.png) ;
; - j, l'indice des constituants,
![j \in \left[1, \cdots , N \right]](../i/m/12d9cfc51778e0accd22af33437990e6.png) ;
; -
 , le coefficient stœchiométrique du constituant j dans la réaction i, tel que :
, le coefficient stœchiométrique du constituant j dans la réaction i, tel que :
-
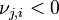 pour un réactif ;
pour un réactif ; -
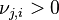 pour un produit ;
pour un produit ; -
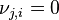 si le constituant j n'intervient pas dans la réaction i.
si le constituant j n'intervient pas dans la réaction i.
-
Soit 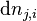 la variation de quantité du constituant j due à la réaction i. À noter que l'on a
la variation de quantité du constituant j due à la réaction i. À noter que l'on a 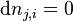 si
si 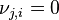 , c'est-à-dire que le constituant j n'intervient pas dans la réaction i.
, c'est-à-dire que le constituant j n'intervient pas dans la réaction i.
Pour chacun des N constituants, on a la variation globale de quantité dans le mélange réactionnel  :
:
Pour chacune des M réactions, on définit un avancement de réaction  tel que pour chacun des N constituants :
tel que pour chacun des N constituants :
On a donc pour tout ![j \in \left[1, \cdots , N \right]](../i/m/12d9cfc51778e0accd22af33437990e6.png) :
:
Le potentiel chimique de chacun des N constituants est défini sur l'ensemble du mélange réactionnel. La variation à pression et température constantes de l'enthalpie libre globale du système réactionnel vaut alors :
avec 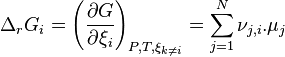 l'enthalpie libre de réaction de la réaction i.
l'enthalpie libre de réaction de la réaction i.
Pour chacun des N constituants, réactif, produit ou inerte, la quantité varie au cours du temps selon :
avec :
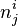 , la quantité du constituant j à l'instant initial t = 0 ;
, la quantité du constituant j à l'instant initial t = 0 ;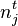 , la quantité du constituant j à l'instant t ;
, la quantité du constituant j à l'instant t ;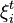 , l'avancement de réaction i à l'instant t ; rappelons qu'à l'instant initial, par définition,
, l'avancement de réaction i à l'instant t ; rappelons qu'à l'instant initial, par définition, 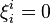 .
.
Les potentiels chimiques sont des fonctions de l'ensemble des quantités des N constituants du mélange réactionnel : 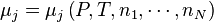 . Chacune des M enthalpies de réaction est donc fonction de l'ensemble des M avancements de réaction :
. Chacune des M enthalpies de réaction est donc fonction de l'ensemble des M avancements de réaction :
Constantes d'équilibre, quotients de réaction et lois d'action de masse
Pour chacun des N constituants, on choisit un état standard unique, valable pour l'ensemble des M réactions. Le potentiel chimique 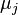 du constituant j dans le mélange réactionnel est lié au potentiel
du constituant j dans le mélange réactionnel est lié au potentiel 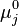 du constituant dans son état standard par une activité chimique
du constituant dans son état standard par une activité chimique 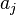 telle que :
telle que :
L'activité du constituant j est donc également unique et valable pour l'ensemble des M réactions du mélange réactionnel. Pour chacune des M réactions simultanées, on peut définir une constante d'équilibre 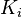 et un quotient de réaction
et un quotient de réaction 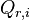 :
:
Pour chacune des M réactions on a les mêmes relations que pour une réaction seule :
- si
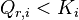 , alors
, alors 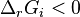 et
et 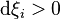 : la réaction i progresse ;
: la réaction i progresse ; - si
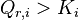 , alors
, alors 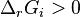 et
et 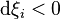 : la réaction i régresse ;
: la réaction i régresse ; - si
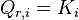 , alors
, alors 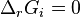 : la réaction i est à l'équilibre.
: la réaction i est à l'équilibre.
À l'équilibre, on a donc pour chacune des M réactions une loi d'action de masse :
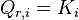 pour tout
pour tout ![i \in \left[1, \cdots , M \right]](../i/m/624bce5eb67eeadea4896bf75700f5fd.png)
Critère d'évolution spontanée, condition d'équilibre et condition de stabilité
Le deuxième principe de la thermodynamique induit que l'enthalpie libre globale du système réactionnel ne peut que décroître :
Critère d'évolution spontanée de tout système chimique à P et T constantes : 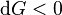 |
L'équilibre correspond alors au minimum de la fonction  , soit
, soit 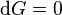 ; ceci implique que l'enthalpie libre de réaction de chacune des M réactions est nulle. On obtient ainsi un ensemble de M équations à M inconnues (les avancements
; ceci implique que l'enthalpie libre de réaction de chacune des M réactions est nulle. On obtient ainsi un ensemble de M équations à M inconnues (les avancements  ) :
) :
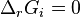 pour tout
pour tout ![i \in \left[1, \cdots , M \right]](../i/m/624bce5eb67eeadea4896bf75700f5fd.png)
On note à l'aide de l'opérateur nabla le gradient de la fonction  :
:
Il s'agit d'un ensemble de M fonctions des M avancements de réaction  . L'équilibre est donc atteint lorsque le gradient est nul :
. L'équilibre est donc atteint lorsque le gradient est nul :
Condition d'équilibre : 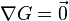 |
Comme pour une réaction seule, la solution mathématique de 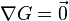 n'est pas forcément unique. Il convient donc également, lors d'une simulation numérique d'un système réactionnel à réactions simultanées, de vérifier que la solution obtenue en annulant les enthalpies de réaction est bien un minimum stable de la fonction
n'est pas forcément unique. Il convient donc également, lors d'une simulation numérique d'un système réactionnel à réactions simultanées, de vérifier que la solution obtenue en annulant les enthalpies de réaction est bien un minimum stable de la fonction  globale du système réactionnel. Cette condition est vérifiée si la matrice hessienne
globale du système réactionnel. Cette condition est vérifiée si la matrice hessienne  de la fonction
de la fonction  est définie positive pour la solution de
est définie positive pour la solution de 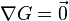 :
:
Condition de stabilité de l'équilibre : à l'équilibre la matrice hessienne  de de  est définie positive. est définie positive. |
Plutôt que de résoudre d'abord le système de M équations à M inconnues et de tester a posteriori la stabilité des diverses solutions, il est préférable de rechercher la meilleure solution directement à l'aide d'un algorithme de minimisation sous contrainte (par exemple la méthode des multiplicateurs de Lagrange) appliqué à la fonction  globale, les contraintes étant que la quantité de chacun des N constituants doit rester positive et que la masse globale du système réactionnel est conservée.
globale, les contraintes étant que la quantité de chacun des N constituants doit rester positive et que la masse globale du système réactionnel est conservée.
Notes
- ↑ Le terme de réaction réversible peut porter à confusion, il ne s'agit pas en effet d'une transformation réversible, ne créant pas d'entropie. De même, le terme de réaction partielle ou incomplète peut s'appliquer à une réaction totale dont les réactifs n'ont pas été introduits en stœchiométrie, par exemple une combustion en défaut d'air. Il est donc préférable d'employer le terme de réaction inversible, cf. portail Dunod de la chimie organique.
- ↑ SABIX - Société des amis de la bibliothèque et de l'histoire de l'École polytechnique - Bulletin n°23 (avril 2000) - Biographie de Berthollet
- ↑ SABIX - Société des amis de la bibliothèque et de l'histoire de l'École polytechnique - Bulletin n°24 (août 2000) - Berthollet et la théorie des affinités
- ↑ Ilya Prigogine, Raymond Defay, « Traité de thermodynamique, conformément aux méthodes de Gibbs et de Donder », Éditions Desoer (1950)
- ↑ Raymond Defay (1897-1987), physicien et chimiste belge, professeur à l'Université libre de Bruxelles, cf. IdRef.
- ↑ G. Lefebvre, « Notions de chimie du pétrole », École nationale supérieure du pétrole et des moteurs, Éditions Technip, 1986 (ISBN 2-7108-0512-X)
- ↑ Inaki de Aguirre, Marie-Anne Van de Wiel, « Introduction à la chimie générale », tome 2 chimie minérale, 1re éd., 11e tirage, De Boeck Université, 2000 (ISBN 2-8041-0720-5)
- ↑ Paul Depovere, « Chimie générale », 3e éd., 2e tirage, De Boeck Université, 2006 (ISBN 2-8041-5029-1)
- ↑ Ne pas confondre Claude Louis Berthollet et Marcellin Berthelot.
- ↑ Voir l'article Entropie d'un corps pur.
- ↑ Berthelot énonça son principe, fruit d'un immense travail d'expérimentation et de collecte de données, en 1879. Il espérait le hisser au rang des grandes lois universelles, au même titre que la loi de la gravité de Newton. En 1884, à peine cinq ans plus tard, la thèse soutenue par Duhem, qui introduisait en Europe le formalisme mathématique de l'américain Gibbs, et notamment la fonction
 , annihila tous les espoirs de Berthelot. La querelle qui s'ensuivit entre les deux hommes, mêlant science et politique, ruina la carrière de Duhem. Cf. Prévoir les réactions chimiques : un problème controversé au XIXème siècle par Vangelis Antzoulatos, Laboratoire SCité, Université Lille 1.
, annihila tous les espoirs de Berthelot. La querelle qui s'ensuivit entre les deux hommes, mêlant science et politique, ruina la carrière de Duhem. Cf. Prévoir les réactions chimiques : un problème controversé au XIXème siècle par Vangelis Antzoulatos, Laboratoire SCité, Université Lille 1. - 1 2 Jacques Schwarzentruber (EMAC), « Caractérisation de l'équilibre chimique », ENS des mines d'Albi-Carmaux
- ↑ Jacques Schwarzentruber (EMAC), « Énoncé de la loi d'action de masse », ENS des mines d'Albi-Carmaux
- ↑ Université en ligne, « Calcul de l'enthalpie libre standard de réaction »
- ↑ En toute rigueur, les termes d'équilibre instable et d'équilibre métastable ne sont pas interchangeables. Un équilibre instable est défini par des vitesses de réaction extrêmement faibles, conduisant à une variation de l'avancement de réaction quasi nulle, non mesurable, comme pour la transformation du diamant en graphite. Un équilibre métastable est un équilibre dans lequel les réactions n'ont pas lieu faute d'un facteur déclenchant ; par exemple un mélange d'hydrogène et d'oxygène est métastable, il peut être conservé dans le temps sans variation de composition, mais une simple étincelle déclenche une réaction violente produisant de l'eau. Ce terme s'emploie également dans l'état de surfusion de l'eau.
- ↑ UQUAC, Université du Québec à Chicoutimi, Cours de cinétique chimique, Chapitre I, Caractères généraux de la cinétique des réactions homogènes, Paragraphe 6, Influence de la température sur la vitesse de réaction
- ↑ UQUAC, Université du Québec à Chicoutimi, Cours de cinétique chimique, Chapitre II, Théorie des vitesses de réaction, Paragraphe 4, L'entropie de réaction
- ↑ Michel Soustelle, « Cinétique chimique - éléments fondamentaux », éd. Hermès Science Publications-Lavoisier, 2011 (ISBN 978-2-7462-3002-6)
- ↑ P. Infelta et M. Graetzel, « Thermodynamique », BrownWalker Press, 2006
- ↑ Jacques Schwarzentruber (EMAC), « Effet de la composition globale du système sur le déplacement de la réaction », ENS des mines d'Albi-Carmaux
- ↑ Site Larousse.fr, Archives, Grande Encyclopédie Larousse, Éd. 1971-1976, article Équilibre chimique, page 4925
Voir aussi
Articles connexes
- Réaction chimique
- Deuxième principe de la thermodynamique
- Enthalpie libre
- Potentiel chimique
- Fugacité
- Activité chimique
- Grandeur de réaction
- Constante d'équilibre
- Détermination des constantes d'équilibre
- Relations de Kirchhoff
Bibliographie
- J. Willard Gibbs, traduit par Henry Le Chatelier, « Équilibre des systèmes chimiques », éd. G. Carré et C. Naud (Paris), 1899, Accessible sur Gallica
- Jean-Pierre Corriou, « Thermodynamique chimique - Équilibres thermodynamiques », Techniques de l'ingénieur, base documentaire : Thermodynamique et cinétique chimique, pack : Opérations unitaires. Génie de la réaction chimique, univers : Procédés chimie - bio - agro, J 1028, pp. 1-11, 1985
- Jean Vidal, « Thermodynamique - Application au génie chimique et à l'industrie pétrolière », coll. Publications de l'Institut français du pétrole, Éditions Technip, 1997 (ISBN 978-2-7108-0715-5)
- Portail de la physique
- Portail de la chimie
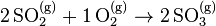
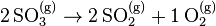
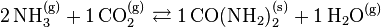
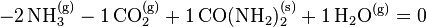

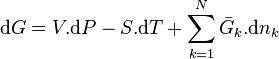
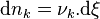
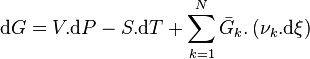
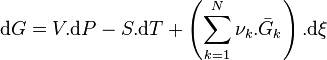
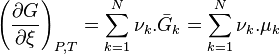
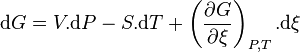
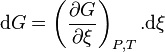
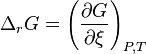
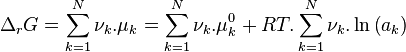
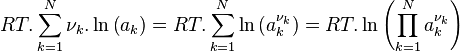
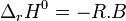 ,
, 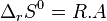 ,
, 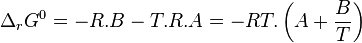

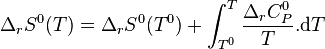
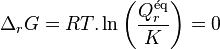
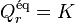
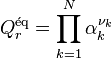
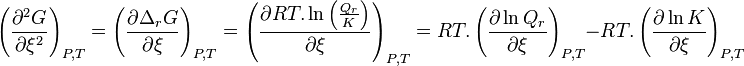
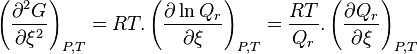
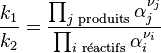
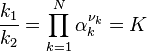
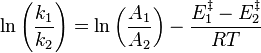
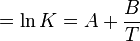
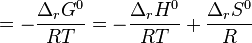
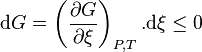
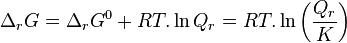
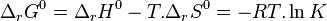
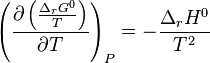

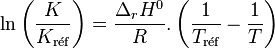
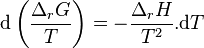
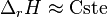
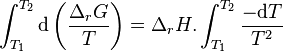
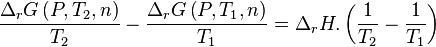
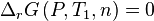
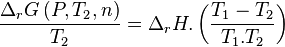
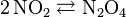

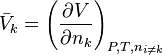
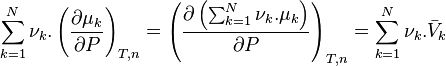
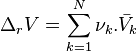
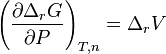
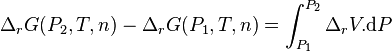

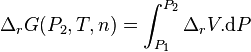
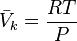
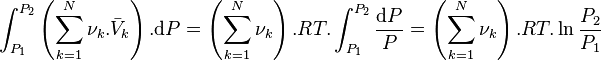
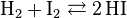
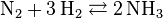
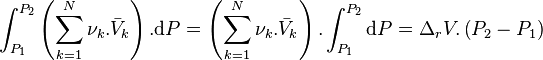
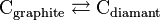
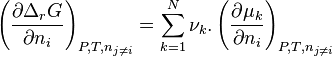
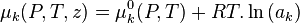
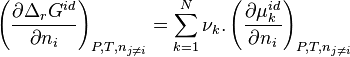
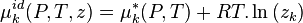
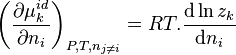
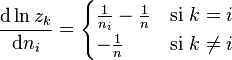
![\left( \frac{\partial \Delta_r G^{id}}{\partial n_i} \right) _{P,T,n_{j \neq i}}
= RT. \left[ \frac{\nu_i}{n_i} - \frac{\sum_{k=1}^{N} \nu_k}{n} \right]](../i/m/f3fbf89fe8c5b2ec4eca9266c88ade14.png)
![\int_{n_i}^{n_i + \Delta n_i} \left( \frac{\partial \Delta_r G^{id}}{\partial n_i} \right) _{P,T,n_{j \neq i}} . \mathrm d n_i
= RT. \int_{n_i}^{n_i + \Delta n_i} \left[ \frac{\nu_i}{n_i} - \frac{\sum_{k=1}^{N} \nu_k}{n} \right]. \mathrm d n_i](../i/m/f635afae71886739e0ada04b22bbca78.png)
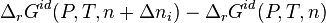
![= RT.\left[ \nu_i . \ln \left( \frac{n_i + \Delta n_i}{n_i} \right)
- \sum_{k=1}^{N} \nu_k. \ln \left( \frac{n + \Delta n_i}{n} \right) \right]](../i/m/2b4348d3970c5b323c02dcfef837c72a.png)
![= RT.\left[ \nu_i . \ln \left(1 + \frac{\Delta n_i}{n_i} \right)
- \sum_{k=1}^{N} \nu_k. \ln \left(1 + \frac{\Delta n_i}{n} \right) \right]](../i/m/dcf57ddb54366e1ec3d4c148f55753f7.png)
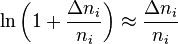
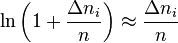
![\approx RT.\left[ \nu_i . \left( \frac{\Delta n_i}{n_i} \right)
- \sum_{k=1}^{N} \nu_k. \left( \frac{\Delta n_i}{n} \right) \right]](../i/m/f9e2b7e56e4d3e45bd8b19cfdb2cb345.png)
![\approx \left[ \nu_i - z_i. \sum_{k=1}^{N} \nu_k \right].\frac{\Delta n_i}{n_i}.RT](../i/m/152b61096636e37da04d024c634e056f.png)
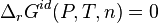
![\Delta_r G^{id}(P,T,n+\Delta n_i) = \left[ \nu_i - z_i. \sum_{k=1}^{N} \nu_k \right].\frac{\Delta n_i}{n_i}.RT](../i/m/c317858a3da80d042623dab95ae5d23a.png)
![\Delta_r G^{id} = \Sigma \nu . \left[\frac{\nu_i}{\Sigma \nu} - z_i \right] . \frac{\Delta n_i}{n_i}. RT](../i/m/18c89aa4e84c3b96791d4b0d0c4570aa.png)
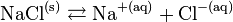
![K_\text{NaCl} = \rm \left[ Na^+ \right].\left[ Cl^- \right]](../i/m/085dd40a839a159003a158322500f9f4.png)
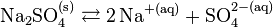
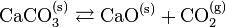
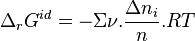
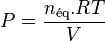
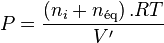
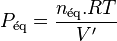
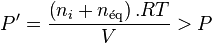
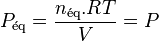
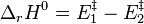
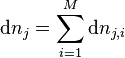
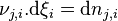
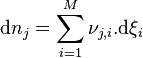
![\mathrm dG = \sum_{j=1}^{N} \mu_{j}. \mathrm dn_{j} = \sum_{j=1}^{N} \mu_{j}. \left[ \sum_{i=1}^{M} \nu_{j,i}.\mathrm d \xi_{i} \right]
= \sum_{i=1}^{M} \left[ \sum_{j=1}^{N} \nu_{j,i}.\mu_{j} \right] .\mathrm d \xi_{i} = \sum_{i=1}^{M} \Delta_rG_{i} .\mathrm d \xi_{i}](../i/m/ce6fa663d94d461be5b0ef9c526f7d78.png)