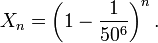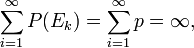Paradoxe du singe savant
Renseignements g??n??raux
Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?

Le singe th??or??me infinie stipule qu'un singe frapper les touches au al??atoire sur un clavier de machine ?? ??crire pour un quantit?? infinie de temps sera presque s??rement taper un texte particulier choisi, tels que les ??uvres compl??tes de William Shakespeare . Dans ce contexte, " presque s??rement "est un terme math??matique avec un sens pr??cis, et le?? singe ??ne est pas un singe r??elle, mais plut??t, ce est une m??taphore pour un dispositif abstrait qui produit une s??quence al??atoire de lettres ?? l'infini. Le th??or??me illustre les p??rils de raisonner sur l'infini en imaginant un vaste, mais nombre fini, et vice versa. La probabilit?? d'un singe tapant une cha??ne donn??e d'un texte aussi longtemps que, par exemple, Hamlet, est si minuscule que, ont ??t?? men??es l'exp??rience, la chance qu'il se produise r??ellement pendant un laps de temps de l'ordre de l' ??ge de l'univers est minuscule mais pas z??ro.
Variantes du th??or??me comprennent de multiples et m??me une infinit?? de dactylographes, et le texte cible varie entre toute une biblioth??que et une seule phrase. L'histoire de ces d??clarations peut ??tre retrac??e ?? Aristote M??taphysique s 'et De natura la deorum de Cic??ron, par Blaise Pascal et Jonathan Swift, et enfin aux ??tats modernes avec leurs machines ?? ??crire embl??matiques. Au d??but du 20e si??cle, ??mile Borel et Arthur Eddington utilis?? le th??or??me pour illustrer les d??lais implicites dans les fondements de la m??canique statistique . Divers Apologistes chr??tiens d'une part, et Richard Dawkins de l'autre, ont fait valoir ?? propos de la pertinence des singes comme une m??taphore de l'??volution .
Aujourd'hui, l'int??r??t populaire pour les singes de frappe est soutenue par de nombreuses apparitions dans la litt??rature, la t??l??vision et la radio, la musique et l'Internet. En 2003, une exp??rience a ??t?? r??alis??e avec humour six C??l??bes Crested macaques, mais leur contribution litt??raire ??tait cinq pages constitu?? en grande partie de la lettre S.
Solution
Preuve directe
Il est une preuve directe de ce th??or??me. Si deux ??v??nements sont statistiquement ind??pendants, (ce est ?? dire ne affecte ni le r??sultat de l'autre), alors la probabilit?? de survenance la fois est ??gale au produit des probabilit??s de chacun d'eux passe de fa??on ind??pendante. Par exemple, si le risque de pluie ?? Sydney un jour donn?? est de 0,3 et la possibilit?? d'un tremblement de terre ?? San Francisco ce jour est de 0,008, alors la chance de passe ?? la fois sur ce m??me jour est de 0,3 ?? 0,008 = 0,0024.
Supposons que la machine dispose de 50 touches, et le mot est tap?? ??tre " banane ". Taper au hasard, la chance que la premi??re lettre tap??e est b est 1/50, et la chance que la deuxi??me lettre tap??e est un 1/50 est aussi, et ainsi de suite, parce que les ??v??nements sont ind??pendants. Donc les chances de la banane six premi??res lettres correspondant est
- (1/50) x (1/50) x (1/50) x (1/50) x (1/50) x (1/50) = (1/50) 6.
Pour la m??me raison, la possibilit?? que les six lettres suivantes correspondent ?? la banane est ??galement (1/50) 6, et ainsi de suite.
De ce qui pr??c??de, la chance de ne pas taper la banane dans un bloc donn?? de 6 lettres est une - (1/50) 6. Parce que chaque bloc est tap?? ind??pendamment, la chance n X de ne pas taper la banane dans l'un des n premiers blocs de six lettres est
Comme pousse n, X n devient plus petit. Pour un n d'un millions, X n est de 99,99%, mais pour un n de 10 milliards de X n est de 53% et pour un n de 100 milliards, il est de 0,17%. Comme n tend vers l'infini, la probabilit?? X n se approche de z??ro; ce est en faisant n suffisamment grand, X n peut ??tre rendue aussi petite que l'on veut.
Le m??me argument montre pourquoi au moins un d'une infinit?? de singes aura (presque s??rement) produire un texte aussi rapidement qu'il serait produite par une dactylo humaine parfaitement exacte copie de l'original. Dans ce cas, X n = (1 - (1/50) 6) n dans laquelle X n repr??sente la probabilit?? qu'aucun des premier n types de singes banane correctement du premier coup. Lorsque nous consid??rons 100000000000 singes, la probabilit?? tombe ?? 0,17%, et que le nombre de singes n augmente ?? l'infini la valeur de X n - la probabilit?? des singes d??faut de reproduire le texte donn?? - diminue ?? z??ro. Cela ??quivaut ?? dire que la probabilit?? qu'un ou plusieurs d'un nombre infini de singes va produire un texte donn?? sur le premier essai est de 100%, ou qu'il est presque certain qu'ils le feront.
Cordes infinies
Les deux d??clarations ci-dessus peuvent ??tre ??nonc??s plus g??n??ralement et de fa??on compacte en termes de cordes, qui sont des s??quences de caract??res choisis parmi un alphabet fini:
- Compte tenu d'une cha??ne infinie o?? chaque caract??re est choisi uniform??ment au hasard, ne importe quelle cha??ne finie donn?? se produit presque s??rement comme une cha??ne ?? une position (et en effet, un nombre infini de positions).
- ??tant donn?? une suite infinie de cha??nes infinies, o?? chaque caract??re de chaque cha??ne est choisi uniform??ment au hasard, ne importe quelle cha??ne finie donn?? se produit presque s??rement comme pr??fixe d'une de ces cha??nes (et en effet, comme un pr??fixe d'une infinit?? de ces cha??nes dans le s??quence).
Ils suivent facilement de la seconde Borel-Cantelli. Pour la deuxi??me th??or??me, soit E k le Si le k ??me cha??ne commence par le texte donn??. Parce que cela a un certain fixe non nul probabilit?? p de se produire, le E k sont ind??pendants, et la somme ci-dessous diverge,
la probabilit?? que nombre infini de l'E k se produisent est 1. Le premier th??or??me est d??montr?? de fa??on similaire; on peut diviser la cha??ne al??atoire en blocs non chevauchants correspondant ?? la taille du texte souhait??, et de faire E k le cas o?? le k ??me bloc est ??gal ?? la cha??ne souhait??e.
Probabilit??s
Ignorance la ponctuation, l'espacement et la capitalisation, un singe tapant les lettres uniform??ment au hasard a une chance sur 26 de taper correctement la premi??re lettre de Hamlet. Il a une chance sur 676 (26 ?? 26) de taper les deux premi??res lettres. Parce que la probabilit?? diminue de fa??on exponentielle , ?? 20 lettres qu'il a d??j?? qu'une chance sur 26 = 20 19,928,148,895,209,409,152,340,197,376, ?? peu pr??s ??quivalent ?? la probabilit?? d'acheter 4 billets cons??cutivement et gagner le jackpot ?? chaque fois loterie. Dans le cas de l'ensemble du texte de Hamlet, les probabilit??s sont si infime qu'ils peuvent ?? peine ??tre con??us en termes humains. Dites le texte de Hamlet contient 130 000 lettres (il est en fait plus, m??me d??pouill?? de ponctuation), alors il ya une probabilit?? de un sur 3,4 ?? 10 183 946 pour obtenir le droit de texte lors du premier proc??s. Le nombre moyen de lettres qui doit ??tre tap?? jusqu'?? ce que le texte se affiche est ??galement 3,4 ?? 10 183 946.
Pour fins de comparaison, il ya seulement environ 3 ?? 10 79 atomes d'hydrog??ne dans l' univers observable et ?? seulement 4,3 ?? 10 17 secondes se sont ??coul??es depuis le Big Bang . M??me si l'univers observable ??tait rempli de singes tapant une fois pour toutes, de leur probabilit?? totale pour produire une seule instance de Hamlet serait encore moins d'un sur 10 183 800. Comme Kittel et Kroemer a dit, "La probabilit?? d'Hamlet est donc nul dans tous les sens op??rationnelle d'un ??v??nement ...", et la d??claration que les singes doivent finalement r??ussir ??donne une conclusion trompeuse sur les tr??s, tr??s grand nombre." Ce est de leur manuel sur la thermodynamique , le domaine dont les fondements statistiques motiv?? les expositions d'abord connus des singes de frappe.
Histoire
M??canique statistique
Dans l'une des formes sous lesquelles probabilistes sais maintenant ce th??or??me, avec son "dactyloscopique" [cf., dactylographie] singes ( fran??ais : singes dactylographes; le mot Fran??ais singe couvre ?? la fois les singes et les singes ), paru dans 1913 article d'??mile Borel "M??canique Statistique et irr??versibilit??" ( de la m??canique statistique et irr??versibilit??), et dans son livre "Le Hasard" en 1914. Ses ??singes?? ne sont pas des singes r??els; plut??t, ils sont une m??taphore de mani??re imaginaire pour produire une grande, s??quence al??atoire de lettres. Borel a dit que si un million de singes saisis dix heures par jour, il est extr??mement peu probable que leur production serait exactement ??gale tous les livres des biblioth??ques les plus riches du monde; et pourtant, en comparaison, ce ??tait encore plus improbable que les lois de la m??canique statistique seraient jamais ??tre viol??s, m??me bri??vement.
Le physicien Arthur Eddington a attir?? sur l'image de Borel plus loin dans la nature du monde physique (1928), ??crit:
Si je laisse mes doigts se prom??nent bras crois??s sur les touches de machine ?? ??crire, il peut arriver que mon chape fait une phrase intelligible. Si une arm??e de singes ont ??t?? Jouant sur les machines ?? ??crire, ils peuvent ??crire tous les livres au British Museum. Le risque de leur faire est nettement plus favorable que le hasard des mol??cules de retour ?? la moiti?? de la cuve.
Ces images invitent le lecteur ?? consid??rer l'incroyable invraisemblance d'un grand mais fini nombre de singes de travail pour une grande mais finie de temps produire un travail important, et de comparer cela avec la plus grande invraisemblance de certains ??v??nements physiques. Tout processus physique qui est encore moins probable que le succ??s de ces singes est effectivement impossible, et il peut dire sans se tromper que ce processus ne se produira jamais.
Origines et "La Biblioth??que totale"
Dans un essai 1939 intitul?? ??La biblioth??que totale", l'??crivain argentin Jorge Luis Borges retrac?? le concept infinie singe retour ?? Aristote M??taphysique s '. Expliquant les vues de Leucippe, qui a estim?? que le monde se pose ?? travers la combinaison al??atoire de atomes , Aristote note que les atomes eux-m??mes sont homog??nes et leurs arrangements possibles ne diff??rent que par la position et l'ordre. Le philosophe grec compare ?? la fa??on dont une trag??die et une com??die se composent des m??mes "atomes", ce est ?? dire, des caract??res alphab??tiques. Trois si??cles plus tard, De natura deorum de Cic??ron (De la nature des Dieux) a argument?? contre la vision du monde atomiste:
Celui qui croit cela peut ainsi croire que si une grande quantit?? de l'un vingt-lettres, compos??es soit d'or ou de toute autre question, ont ??t?? jet??s sur le sol, ils serait tomber dans l'ordonnance lisiblement pour former les Annales de Ennius. Je doute que la fortune pourrait faire un seul verset d'entre eux.
Borges suit l'histoire de cet argument par Blaise Pascal et Jonathan Swift, puis observe que, dans son temps, le vocabulaire a chang??. En 1939, l'idiome ??tait "qu'une demi-douzaine de singes seraient fournies avec les machines ?? ??crire, en quelques ??ternit??s, produire tous les livres au British Museum." (Pour ce qui ajoute Borges, ??Strictement parlant, un singe immortel suffirait.") Borges imagine alors le contenu de la Biblioth??que total dont cette entreprise produirait si elle est men??e ?? son maximum extr??me:
Tout serait dans ses volumes aveugles. Tout: l'histoire d??taill??e de l'avenir, d'Eschyle Les Egyptiens, le nombre exact de fois que les eaux du Gange ont r??fl??chis le vol d'un faucon, la nature secr??te et vrai de Rome, l'encyclop??die Novalis aurait construit, mes r??ves et les demi-r??ves ?? l'aube, le 14 Ao??t 1934, la preuve du th??or??me de Pierre de Fermat, les chapitres non ??crites de Edwin Drood, ces m??mes chapitres traduits dans la langue parl??e par les Garamantes, les paradoxes Berkeley invent?? concernant le temps, mais ne ont pas publi??, Les livres d'Urizen de fer, les ??piphanies pr??matur??s de Stephen Dedalus, qui ne aurait aucun sens avant un cycle de mille ans, le gnostique Evangile de Basilide, le chant des sir??nes chantaient, le catalogue complet de la biblioth??que, la preuve de l'inexactitude de cette catalogue. Tout: mais pour chaque ligne sensible ou fait pr??cise il y aurait des millions de cacophonies signification, farragoes verbales et bavardages. Tout: mais toutes les g??n??rations de l'humanit?? pourraient se ??couler avant que les ??tag??res-??tag??res vertigineuses qui oblit??rent le jour et sur lequel le chaos se trouve jamais les r??compenser avec une page tol??rable.
Concept de biblioth??que totale de Borges ??tait le th??me principal de sa tr??s lu 1941 histoire courte " La Biblioth??que de Babel ", qui d??crit un incroyablement vaste biblioth??que compos??e de verrouillage chambres hexagonales, renfermant ensemble chaque volume possible qui pourrait ??tre compos?? ?? partir des lettres de l'alphabet et quelques caract??res de ponctuation.
Applications et critiques
??volution

Dans son livre 1931 Le myst??rieux Univers, rival Eddington James Jeans attribu?? la parabole de singe ?? un "Huxley", ce qui signifie sans doute Thomas Henry Huxley. Cette attribution est incorrect. Aujourd'hui, il est parfois ??galement signal?? que Huxley appliqu?? l'exemple dans un d??sormais l??gendaire d??bat sur Charles Darwin l ' origine des esp??ces avec l'??v??que anglican d'Oxford, Samuel Wilberforce, tenue lors d'une r??union de la Association britannique pour l'avancement des sciences ?? Oxford en 30 juin 1860. Cette histoire ne souffre pas seulement d'un manque de preuves, mais le fait que, en 1860, la machine ?? ??crire lui-m??me ne avait pas encore ?? ??merger. Primates ??taient toujours un sujet sensible pour d'autres raisons, et le d??bat Huxley-Wilberforce fait inclure byplay sur les grands singes: l'??v??que a demand?? si Huxley descendait d'un singe sur r??pondu de sa grand-m??re ou du c??t?? de son grand-p??re, et Huxley quelque chose ?? l'effet qu'il serait plut??t descendre d'un singe que de quelqu'un qui a fait valoir que malhonn??te que l'??v??que.
Malgr?? le mix-up original, arguments singe et-machine ?? ??crire sont d??sormais courants dans les arguments sur l'??volution. Par exemple, Doug Powell affirme comme un Apologiste chr??tien que m??me si un singe accidentellement types les lettres de Hamlet, il a ??chou?? ?? produire Hamlet parce qu'il ne avait pas l'intention de communiquer. Son implication parall??le est que les lois naturelles ne pouvaient pas produire le contenu de l'information dans l'ADN . Un argument plus commune est repr??sent??e par John MacArthur, qui pr??tend que les mutations g??n??tiques n??cessaires pour produire un t??nia d'une amibe sont aussi improbable comme un singe tapant le soliloque de Hamlet, et donc les chances contre l'??volution de toute vie sont impossibles ?? surmonter.
Le biologiste ??volutionniste Richard Dawkins emploie le concept de singe de frappe dans son livre 1986 L'Horloger aveugle pour d??montrer les capacit??s de la s??lection naturelle dans la production biologique la complexit?? d'al??atoire mutations. Dans l'exp??rience de simulation qu'il d??crit, Dawkins a son programme de Weasel produire la phrase Hamlet me semble, ce est comme une belette en tapant des phrases al??atoires, mais le gel en permanence les parties de la sortie qui correspond d??j?? l'objectif. Le point est que la g??n??ration de cha??ne al??atoire sert simplement ?? fournir des mati??res premi??res, tandis que la s??lection donne l'information.
Une autre avenue pour rejeter l'analogie entre l'??volution et un singe sans contrainte r??side dans le probl??me que les types de singe seule lettre ?? la fois, ind??pendamment des autres lettres. Hugh Petrie fait valoir que une configuration plus sophistiqu??e est n??cessaire, dans son cas, pas pour l'??volution biologique, mais l'??volution des id??es:
Afin d'obtenir l'analogie correcte, nous aurions ?? ??quiper le singe avec une machine ?? ??crire plus complexe. Il devrait inclure des phrases et des pens??es ??lisab??thaine entiers. Il devrait inclure croyances ??lisab??thaines sur les modes d'action humains et les causes, la morale et la science ??lisab??thaine, et des mod??les linguistiques pour exprimer ces. Il serait probablement m??me avoir ?? inclure un compte des sortes d'exp??riences qui ont fa??onn?? la structure de croyance de Shakespeare comme un exemple particulier d'un ??lisab??thaine. Puis, peut-??tre, nous pourrions permettre le singe ?? jouer avec une telle machine ?? ??crire et produire des variantes, mais l'impossibilit?? d'obtenir une pi??ce de Shakespeare ne est plus ??vidente. Ce qui est vraiment vari??e fait encapsuler un grand nombre de connaissances d??j?? atteint.
James W. Valentine, tout en admettant que la t??che du singe classique est impossible, trouve qu'il ya une analogie int??ressante entre l'anglais ??crit et l' m??tazoaires g??nome dans cette autre sens: les deux ont "combinatoires, les structures hi??rarchiques" qui limitent grandement l'immense nombre de combinaisons au niveau de l'alphabet.
La th??orie litt??raire
RG Collingwood a fait valoir en 1938 que l'art ne peut ??tre produit par accident, et a ??crit comme un sarcastique de c??t?? pour ses d??tracteurs,
... Certains ... ont refus?? cette proposition, soulignant que si un singe joue avec une machine ?? ??crire ... il produire ... le texte complet de Shakespeare. Tout lecteur qui n'a rien ?? voir peuvent se amuser ?? calculer combien de temps il faudrait pour que la probabilit?? d'??tre la peine de parier sur. Mais l'int??r??t de la suggestion r??side dans la r??v??lation de l'??tat mental d'une personne qui peut identifier les ????uvres?? de Shakespeare avec la s??rie de lettres imprim??es sur les pages d'un livre ...
Nelson Goodman a pris la position contraire, illustrant son point avec Catherine Elgin par l'exemple de Borges " Pierre M??nard, auteur du Quichotte ??,
Que Menard ??crit est tout simplement une autre inscription du texte. Chacun d'entre nous peut faire la m??me chose, que les presses d'impression bo??te et les photocopieurs. En effet, nous dit-on, si un nombre infini de singes ... une finiraient par produire une r??plique du texte. Ce r??plique, nous maintenons, serait autant une instance du travail, Don Quichotte, de Cervant??s que le manuscrit, le manuscrit de Menard, et chaque exemplaire du livre qui ait jamais ??t?? ou seront imprim??s.
Dans un autre ??crit, Goodman d??veloppe, "que le singe peut ??tre cens?? avoir produit sa copie fait au hasard aucune diff??rence. Ce est le m??me texte, et il est ouvert ?? tous les m??mes interpr??tations ...." G??rard Genette rejette l'argument de Goodman que la mendicit?? la question.
Pour Jorge JE Gracia, la question de l'identit?? des textes conduit ?? une autre question, celle de auteur. Si un singe est capable de taper Hamlet, malgr?? l'absence d'intention de sens et donc se disqualifiant en tant qu'auteur, il appara??t que les textes ne ont pas besoin auteurs. Les solutions possibles sont disant que celui qui trouve le texte et l'identifie comme Hamlet est l'auteur; ou que Shakespeare est l'auteur, le singe son agent, et le viseur simplement un utilisateur du texte. Ces solutions ont leurs propres difficult??s, en ce que le texte semble avoir un sens distinct des autres agents: si le singe fonctionne avant Shakespeare est n??, ou si Shakespeare ne est jamais n??, ou si on ne trouve jamais le tapuscrit du singe?
G??n??ration de nombres al??atoires
Le th??or??me concerne un pens?? exp??rience qui ne peuvent ??tre pleinement r??alis??e dans la pratique, car il est pr??vu d'exiger des montants prohibitifs de temps et de ressources. N??anmoins, il a inspir?? des efforts dans la g??n??ration al??atoire finie texte.
Un programme informatique g??r?? par Dan Oliver de Scottsdale, en Arizona, selon un article paru dans The New Yorker, est venu avec un r??sultat le 4 Ao??t 2004: Apr??s que le groupe avait travaill?? pour 42162500000 milliards de milliards d'ann??es, l'un des ??singes?? dactylographi??es, "VALENTINE. Cessez toIdor: eFLP0FRjWK78aXzVOwm) - '; 8.t. . . "Les premiers 19 lettres de cette s??quence peuvent ??tre trouv??s dans" Les Deux Gentilshommes de V??rone ". D'autres ??quipes ont reproduit 18 caract??res de" Timon d'Ath??nes ", 17 de" Troilus et Cressida ", et 16 de" Richard II ".
Un site web intitul?? The Monkey Shakespeare Simulator, lanc?? le 1er juillet 2003 , contenait une applet Java qui simule une grande population de singes tapant au hasard, avec l'intention d??clar??e de voir combien de temps il prend les singes virtuels pour produire une pi??ce de Shakespeare compl??te du d??but ?? la fin. Par exemple, on produit ?? partir de cette ligne partielle Henry IV, partie 2, les rapports qu'il a fallu "2.737.850 millions de milliards de milliards de milliards d'ann??es-singe" pour atteindre 24 caract??res correspondants:
- RUMEUR. Ouvrez vos oreilles; 9R "5J5 &? OWTY Z0d ...
En raison des limitations de puissance de traitement, le programme utilise un mod??le probabiliste (en utilisant un G??n??rateur de nombres al??atoires ou RNG) au lieu de g??n??rer effectivement moins al??atoire et le comparer ?? Shakespeare. Lorsque le simulateur "d??tecte un match" (qui est, le RNG g??n??re une certaine valeur ou une valeur dans une certaine fourchette), le simulateur simule le match en g??n??rant texte correspondant.
Questions sur les statistiques d??crivant combien de fois un singe id??al devront taper certaines cha??nes peuvent motiver des tests pratiques pour g??n??rateurs de nombres al??atoires ainsi; ceux-ci vont de la simple ?? la "tr??s sophistiqu??s". professeurs d'informatique George Marsaglia et Arif Zaman rapport qu'ils ont utilis?? pour appeler ces tests "m- chevauchement tests de tuple "en lecture, car ils concernent chevauchement m-uplets d'??l??ments successifs dans un ordre al??atoire. Mais ils ont constat?? que les qualifiant de?? tests de singe "ont aid?? ?? motiver l'id??e avec les ??l??ves. Ils ont publi?? un rapport sur la classe de tests et leur r??sultats pour diverses RNG en 1993.
Vrais singes
Comportementalistes primates Cheney et Seyfarth remarque que les vrais singes seraient effectivement avoir ?? compter sur la chance pour avoir un espoir de produire Rom??o et Juliette . Contrairement singes et en particulier les chimpanz??s , les donn??es indiquent que les singes ne ont pas de th??orie de l'esprit et qui sont incapables de faire la diff??rence entre leur propre et les connaissances des autres, les ??motions et les croyances. M??me si un singe pourrait apprendre ?? ??crire une pi??ce et d??crire les caract??res de comportement, il ne pouvait pas r??v??ler les caract??res de l'esprit et ainsi de construire une trag??die ironique.
En 2003, les professeurs et les ??tudiants de la Universit?? de Plymouth cours MediaLab Arts utilis?? une subvention ?? 2000 de la Conseil des arts d'??tudier la production litt??raire de vrais singes. Ils ont laiss?? un clavier d'ordinateur dans l'enceinte de six C??l??bes Crested macaques dans Paignton Zoo Devon en Angleterre pendant un mois, avec une liaison radio de diffuser les r??sultats sur un site Web. Un chercheur, Mike Phillips, a d??fendu les d??penses comme ??tant moins cher que la t??l??-r??alit?? et encore ??tr??s stimulant et la visualisation fascinante".
Non seulement les singes ne produisent rien, mais cinq pages constitu?? en grande partie de la lettre S, le m??le plomb a commenc?? par d??nigrer le clavier avec une pierre, et les singes poursuivie par uriner et d??f??quer sur elle. Responsable scientifique du zoo fait remarquer que l'exp??rience avait ??peu de valeur scientifique, sauf ?? d??montrer que la th??orie 'de singe infini?? est erron??e ". Phillips a d??clar?? que le projet de l'artiste financ?? ??tait surtout l'art de la performance, et ils avaient appris "??norm??ment" de lui. Il a conclu que les singes ??ne sont pas g??n??rateurs al??atoires. Ils sont plus complexe que cela. ... Ils ??taient tr??s int??ress??s ?? l'??cran, et ils ont vu que quand ils ont tap?? une lettre, quelque chose se est pass??. Il y avait un niveau d'intention l??-bas."
La culture populaire
Le th??or??me de singe infini et son imagerie associ?? est consid??r?? comme un populaire et illustration proverbiale des math??matiques de la probabilit??, largement connu du grand public en raison de sa transmission par la culture populaire plut??t que du fait de sa transmission par la salle de classe.
Le caract??re durable, r??pandue et populaire de la connaissance du th??or??me a ??t?? not?? dans l'introduction ?? un document de 2001, "Les singes, les machines ?? ??crire et R??seaux - Internet dans la lumi??re de la th??orie d'excellence accidentel?? (Hoffmann et Hofmann). En 2002, un Article du Washington Post a d??clar??: "Beaucoup de gens ont eu du plaisir avec la fameuse id??e que un nombre infini de singes avec un nombre infini de machines ?? ??crire et une quantit?? infinie de temps pourrait ??ventuellement ??crire les ??uvres de Shakespeare." En 2003, le mentionn?? pr??c??demment Conseil des arts financ?? exp??rience impliquant de vrais singes et un clavier d'ordinateur a re??u une couverture m??diatique g??n??ralis??e. En 2007, le th??or??me a ??t?? r??pertori?? par Le magazine Wired dans une liste de huit classique exp??riences de pens??e.
L'histoire de l'imagerie des ??singes de frappe?? remonte au moins aussi loin que l'utilisation de Borel de la m??taphore dans son essai de 1913, et cette imagerie a r??cidiv?? ?? plusieurs reprises depuis dans une vari??t?? de m??dias. Aujourd'hui, l'int??r??t populaire pour les singes de frappe est soutenue par de nombreuses apparitions dans la litt??rature, la t??l??vision et la radio, la musique et l'Internet, ainsi que des romans graphiques et stand-up routines de com??die.