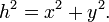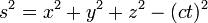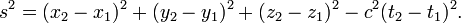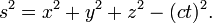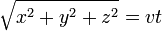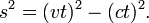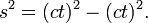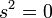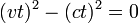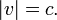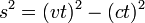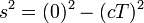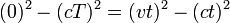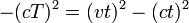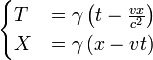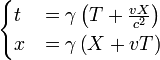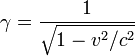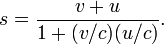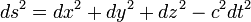Introducci??n a la relatividad especial

Temas relacionados: Matem??ticas ; F??sica

Sab??as ...

Organizar una selecci??n Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/

Albert Einstein durante una conferencia en Viena en 1921

En la f??sica , la relatividad especial es un derecho fundamental teor??a referente espacio y tiempo , desarrollada por Albert Einstein en 1905 como una modificaci??n de La relatividad de Galileo. (Ver " Historia de la relatividad especial "para una descripci??n detallada y las contribuciones de Hendrik Lorentz y Henri Poincar??.) La teor??a era capaz de explicar algunos de prensado te??ricos y experimentales temas en la f??sica del tiempo que involucran luz y electrodin??mica, tales como el fracaso de la 1.887 Experimento de Michelson-Morley, cuyo objetivo era medir las diferencias en la velocidad relativa de la luz debido a la El movimiento de la Tierra a trav??s de la hipot??tica, y ahora desacreditado, ??ter luminoso . A continuaci??n, el ??ter se consider?? el medio de propagaci??n de las ondas electromagn??ticas , tales como luz.

Einstein postul?? que la velocidad de la luz en el espacio libre es el mismo para todos observadores, independientemente de su movimiento en relaci??n con la fuente de luz, donde podemos pensar de un observador como una entidad imaginaria con un sofisticado conjunto de dispositivos de medici??n, en reposo con respecto a s?? mismo, que registran perfectamente las posiciones y los tiempos de todos los eventos en el espacio y el tiempo. Este postulado se deriva de la suposici??n de que las ecuaciones de Maxwell del electromagnetismo , que predicen una velocidad espec??fica de la luz en el vac??o, tienen en cualquier sistema de referencia inercial y no, como se cre??a anteriormente, s??lo en el marco del ??ter. Esta predicci??n contradice las leyes de la mec??nica cl??sica , que hab??an sido aceptadas por siglos, con el argumento de que el tiempo y el espacio no son fijos y en el cambio hecho para mantener una velocidad constante de la luz, independientemente de los movimientos relativos de las fuentes y de los observadores. El enfoque de Einstein se bas?? en pensado experimentos, c??lculos, y el principio de la relatividad, que es la idea de que todas las leyes f??sicas deben aparecer los mismos (es decir, tomar la misma forma b??sica) para todos los observadores inerciales. Hoy en d??a, los cient??ficos est??n tan a gusto con la idea de que la velocidad de la luz es siempre la misma que la metro se define ahora como "la longitud del trayecto recorrido por la luz en el vac??o durante un intervalo de tiempo de 1/299 792 458 de segundo." Esto significa que la velocidad de la luz es por convenci??n 299 792 458 m / s (aproximadamente 1079 millones kilometros por hora, o 671 millones millas por hora).

Las predicciones de la relatividad especial son casi id??nticas a las de la relatividad de Galileo para la mayor??a de los fen??menos cotidianos, en los que las velocidades son mucho m??s baja que la velocidad de la luz, pero hace diferentes predicciones, no evidentes para objetos que se mueven a velocidades muy altas. Estas predicciones se han probado experimentalmente en numerosas ocasiones desde el inicio de la teor??a y fueron confirmadas por los experimentos. Las principales predicciones de la relatividad especial son:

La relatividad de la simultaneidad: Los observadores que se encuentren en movimiento con respecto a la otra pueden estar en desacuerdo sobre si dos hechos ocurrieron al mismo tiempo o uno ocurrieron antes que el otro.
La dilataci??n del tiempo (Un observador viendo dos relojes id??nticos, uno en movimiento y uno en reposo, medir?? el reloj en movimiento a marcar m??s lentamente)
Longitud de contracci??n (lo largo de la direcci??n del movimiento, una varilla que se mueve con respecto a un observador se medir?? a ser m??s corto que una varilla id??ntica en reposo), y
La equivalencia de masa y energ??a (escrito como E = mc ^2).

La relatividad especial predice una no lineal Adem??s f??rmula velocidad que impide velocidades mayores que la de la luz de ser observado. En 1908, Hermann Minkowski reformul?? la teor??a basada en diferentes postulados de car??cter m??s geom??trico. Este enfoque considera espacio y el tiempo como diferentes componentes de una misma entidad, el el espacio-tiempo, que se "divide" de diferentes maneras por los observadores en movimiento relativo. Del mismo modo, la energ??a y el impulso son los componentes de la cuatro impulso, y la el??ctrica y campo magn??tico son los componentes de la tensor electromagn??tico.

Como la relatividad de Galileo se considera ahora una aproximaci??n de la relatividad especial, v??lida para velocidades bajas, la relatividad especial se considera una aproximaci??n de la teor??a de la relatividad general v??lida para d??biles campos gravitatorios. La relatividad general postula que las leyes f??sicas deben aparecer la misma para todos los observadores (una aceleraci??n de marco de referencia equivalente a aquella en la que un gravitacionales actos de campo) y que la gravitaci??n es el efecto de la curvatura del espacio-tiempo causado por la energ??a (incluida la masa).

La f??sica cl??sica y el electromagnetismo

A trav??s de la era entre Newton y alrededor del inicio del siglo 20, el desarrollo de la f??sica cl??sica hab??a hecho grandes progresos. Aplicaci??n de la de Newton ley del cuadrado inverso de la gravedad era la llave para abrir una amplia variedad de eventos f??sicos, desde el calor de la luz , y el c??lculo hizo el c??lculo directo de estos efectos tratable. Con el tiempo, nuevas t??cnicas matem??ticas, en particular el Lagrange, simplificado en gran medida la aplicaci??n de las leyes f??sicas a problemas m??s complejos.

Como la electricidad y el magnetismo estaban mejor exploradas, se hizo evidente que los dos conceptos estaban relacionados. Con el tiempo, este trabajo culmin?? en las ecuaciones de Maxwell , un conjunto de cuatro ecuaciones que podr??an ser utilizados para calcular la totalidad de electromagnetismo. Uno de los resultados m??s interesantes de la aplicaci??n de estas ecuaciones es que era posible construir una onda auto-sostenible de campos el??ctricos y magn??ticos que pueden propagar a trav??s del espacio. Cuando se reduce, la matem??ticas demostr?? que la velocidad de propagaci??n era dependiente de dos constantes universales, y su relaci??n era de la velocidad de la luz . La luz era una onda electromagn??tica.

Bajo el modelo cl??sico, las ondas son desplazamientos dentro de un medio. En el caso de la luz, se pensaba que las ondas de ser desplazamientos de un medio especial conocido como el ??ter luminoso , que se extend??a a trav??s de todo el espacio. Siendo este el caso, la luz viaja en su propio marco de referencia, el marco del ??ter. De acuerdo con el Galileo transformar, debemos ser capaces de medir la diferencia de velocidades entre el marco del ??ter y cualquier otro - un marco universal, por fin.

Dise??ar un experimento para ejercer efectivamente esta medida result?? muy dif??cil, sin embargo, ya que las velocidades y tiempos involucrados hicieron una medici??n precisa dif??cil. El problema de la medida fue finalmente resuelto con la Experimento de Michelson-Morley. Para sorpresa de todos, no se observ?? movimiento relativo. O bien el ??ter estaba viajando a la misma velocidad que la Tierra, dif??cil de imaginar dado movimiento complejo de la Tierra, o no hab??a ??ter. Seguimiento de experimentos probaron varias posibilidades, y por el inicio del siglo 20 que era cada vez m??s dif??cil escapar a la conclusi??n de que no exist??a el ??ter.

Estos experimentos mostraron que todos la luz simplemente no sigui?? la transformaci??n de Galileo. Y, sin embargo, estaba claro que los objetos f??sicos emiten luz, lo que dio lugar a problemas no resueltos. Si uno fuera a llevar a cabo el experimento en el tren de "arrojar luz" en lugar de pelotas, si la luz no sigue la transformaci??n de Galileo entonces los observadores no deben estar de acuerdo en los resultados. Sin embargo, era evidente que el universo estaba en desacuerdo; sistemas f??sicos que se sabe que a grandes velocidades, como estrellas distantes, ten??an la f??sica que eran tan similares a las nuestras como las medidas permitidas. Una especie de transformaci??n tuvo que actuar sobre la luz, o mejor, una sola transformaci??n para la luz y la materia.

El desarrollo de una transformaci??n adecuada para reemplazar la transformaci??n de Galileo es la base de la relatividad especial.

La invariancia de la longitud: la imagen de Euclides

Teorema de Pitagoras

En la relatividad especial, el espacio y el tiempo se unen en un continuo de cuatro dimensiones unificada llamada espacio tiempo. Para tener una idea de lo que el espacio-tiempo es como, primero tenemos que mirar el espacio euclidiano de la f??sica cl??sica newtoniana. Este enfoque para explicar la teor??a de la relatividad especial comienza con el concepto de " longitud ".

En la experiencia cotidiana, parece que la longitud de objetos sigue siendo el mismo, no importa la forma en que se giran o se mueven de un lugar a otro; como resultado de la longitud sencilla de un objeto no parece cambiar o es invariante. Sin embargo, como se muestra en las ilustraciones siguientes, lo que se est?? sugerido en realidad es que la longitud parece ser invariante en un sistema de coordenadas tridimensional.

La longitud de una l??nea en una de dos dimensiones del sistema de coordenadas cartesianas es dada por el teorema de Pit??goras :

$h ^ 2 = x ^ 2 + y ^ 2. \,$

Uno de los teoremas b??sicos de ??lgebra vectorial es que la longitud de un vector no cambia cuando se gira. Sin embargo, una inspecci??n m??s cercana nos dice que esto s??lo es cierto si tenemos en cuenta las rotaciones confinados al plano. Si introducimos la rotaci??n en la tercera dimensi??n, entonces podemos inclinar la l??nea de salida del avi??n. En este caso la proyecci??n de la l??nea en el avi??n obtendr?? m??s corto. ??Esto significa cambios en la longitud de la l??nea? - Obviamente no. El mundo es tridimensional y en un sistema de coordenadas cartesiano 3D de la longitud est?? dada por la versi??n tridimensional del teorema de Pit??goras:

$k ^ 2 = x ^ 2 + y ^ 2 + z ^ 2. \,$

Este es invariante bajo todas las rotaciones. La aparente violaci??n de la invariancia de longitud s??lo ocurri?? porque est??bamos "perdiendo" una dimensi??n. Parece que, a condici??n de todas las direcciones en las que un objeto puede inclinarse o dispuestos est??n representados dentro de un sistema de coordenadas, la longitud de un objeto no cambia bajo rotaciones. Con el tiempo y el espacio considerado como fuera del campo de la f??sica misma, en virtud de la mec??nica cl??sica de un sistema de coordenadas 3-dimensional es suficiente para describir el mundo.

Tenga en cuenta que la invariancia de longitud no se considera normalmente un principio o ley, ni siquiera un teorema. Se trata simplemente de una declaraci??n sobre la naturaleza fundamental del espacio mismo. El espacio como nosotros la concebimos ordinariamente se llama tridimensional espacio euclidiano , porque su estructura geom??trica es descrito por los principios de la geometr??a euclidiana . La f??rmula para la distancia entre dos puntos es una propiedad fundamental de un espacio euclidiano, se llama el tensor de m??trica euclidiana (o simplemente la m??trica euclidiana). En general, las f??rmulas de distancia se llaman tensores m??tricos.

Tenga en cuenta que las rotaciones est??n fundamentalmente relacionados con el concepto de longitud. De hecho, se puede definir la longitud o la distancia a ser la que sigue siendo el mismo (es invariante) bajo rotaciones, o definir las rotaciones a ser la que mantener la longitud invariante. Dada cualquiera, es posible encontrar la otra. Si conocemos la f??rmula de la distancia, podemos encontrar la f??rmula para la transformaci??n de coordenadas en una rotaci??n. Si, por otro lado, tenemos la f??rmula para rotaciones entonces podemos encontrar la f??rmula de la distancia.

La formulaci??n de Minkowski: introducci??n del espacio-tiempo

Despu??s de Einstein deriva relatividad especial formalmente del (a primera vista contra-intuitivo) de que la velocidad de la luz es la misma para todos los observadores, Hermann Minkowski basa en m??todos matem??ticos utilizados en la geometr??a no euclidiana y en el trabajo matem??tico de Lorentz y Poincar??. Minkowski demostr?? en 1908 que la nueva teor??a de Einstein tambi??n podr??a explicarse mediante la sustituci??n del concepto de un espacio y el tiempo por separado con un continuo de cuatro dimensiones llamada espacio-tiempo. Este era un concepto innovador, y Roger Penrose ha dicho que la relatividad no era verdaderamente completo hasta Minkowski reformul?? el trabajo de Einstein.

El concepto de un espacio de cuatro dimensiones es dif??cil de visualizar. Puede ayudar a principios de pensar simplemente en t??rminos de coordenadas. En el espacio tridimensional, se necesita tres n??meros reales para referirse a un punto. En el El espacio de Minkowski, uno necesita cuatro n??meros reales (tres coordenadas espaciales y una coordenada de tiempo) para referirse a un punto en un instante particular de tiempo. Este punto, especificado por las cuatro coordenadas, se denomina evento. La distancia entre dos eventos diferentes se denomina intervalo de espacio-tiempo.

Un camino a trav??s del espacio-tiempo de cuatro dimensiones (generalmente conocido como el espacio de Minkowski) se llama l??nea del mundo. Ya que especifica la posici??n y el tiempo, una part??cula que tiene una l??nea de mundo conocido tiene una trayectoria completamente determinado por la velocidad. Esto es igual que graficar el desplazamiento de una part??cula que se mueve en l??nea recta contra el tiempo transcurrido. La curva contiene la informaci??n motional completa de la part??cula.

En la misma forma que la medici??n de la distancia en el espacio 3D necesaria todas las tres coordenadas, debemos incluir tiempo, as?? como las tres coordenadas espaciales en el c??lculo de la distancia en el espacio de Minkowski (en adelante denominado M). En un sentido, el intervalo de espacio-tiempo proporciona una estimaci??n combinada de hasta qu?? punto se producen dos eventos separados en el espacio, as?? como el tiempo que transcurre entre su ocurrencia.

Pero hay un problema; tiempo est?? relacionado con las coordenadas espaciales, pero no son equivalentes. Teorema de Pit??goras trata a todas las coordenadas en igualdad de condiciones (v??ase el espacio euclidiano para m??s detalles). Podemos intercambiar los dos coordenadas espaciales sin cambiar la longitud, pero no podemos simplemente intercambiar un espacio de coordenadas con el tiempo - son fundamentalmente diferentes. Es una cosa totalmente diferente para dos eventos para ser separados en el espacio y para ser separados en el tiempo. Minkowski propuso que la f??rmula para la distancia necesitaba un cambio. ??l encontr?? que la f??rmula correcta era en realidad bastante simple, que s??lo difieren por una se??al del teorema de Pit??goras:

$s ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 - (ct) ^ 2 \,$

donde c es una constante y t es el tiempo de coordenadas. La multiplicaci??n por c, que tiene la dimensiones L T ^-1, convierte el tiempo para unidades de longitud y esta constante tiene el mismo valor que la velocidad de la luz . De modo que el intervalo de espacio-tiempo entre dos eventos distintos se da por

$s ^ 2 = (x_2 - x_1) ^ 2 + (y_2 - y_1) ^ 2 + (Z_2 - z_1) ^ 2 - c ^ 2 (t_2 - t_1) ^ 2. \,$

Hay dos puntos importantes que deben observarse. En primer lugar, el tiempo se mide en las mismas unidades que la longitud multiplic??ndolo por un factor de conversi??n constante. En segundo lugar, y m??s importante, el tiempo de coordenada tiene un signo diferente de las coordenadas espaciales. Esto significa que en el espacio-tiempo de cuatro dimensiones, una coordenada es diferente a los dem??s e influye en la distancia de manera diferente. Esta nueva "distancia" puede ser cero o incluso negativo. Esta nueva f??rmula de la distancia, llamada m??trica del espacio-tiempo, est?? en el coraz??n de la relatividad. Esta f??rmula de la distancia se denomina tensor m??trico de M. Este signo menos significa que gran parte de nuestra intuici??n sobre las distancias no se puede realizar directamente sobre en intervalos de espacio-tiempo. Por ejemplo, el intervalo de espacio-tiempo entre dos eventos separados tanto en el tiempo y en el espacio puede ser cero (ver abajo). A partir de ahora, la f??rmula t??rminos de distancia y tensor m??trico se utilizar??n indistintamente, ya que ser??n los t??rminos de intervalos Minkowski m??trico y el espacio-tiempo.

En el espacio-tiempo de Minkowski el intervalo de espacio-tiempo es la longitud invariante, la longitud 3D ordinario no se requiere que sea invariante. El intervalo de espacio-tiempo debe permanecer el mismo bajo las rotaciones, pero longitudes ordinarios puede cambiar. Al igual que antes, nos faltaba una dimensi??n. Tenga en cuenta que todo lo que hasta ahora es meramente definiciones. Definimos una construcci??n matem??tica de cuatro dimensiones que tiene una f??rmula especial para la distancia, donde la distancia significa que que se mantiene las mismas rotaciones menores (Alternativamente, se puede definir una rotaci??n a ser la que mantiene la distancia sin cambios).

Ahora viene la parte f??sica. Las rotaciones en el espacio de Minkowski tienen una interpretaci??n diferente de las rotaciones ordinarias. Estas rotaciones corresponden a las transformaciones de los sistemas de referencia. El paso de un sistema de referencia a otra corresponde a girar el espacio de Minkowski. Una justificaci??n intuitiva para esto se da m??s adelante, pero matem??ticamente es un postulado din??mico al igual que el supuesto de que las leyes f??sicas deben permanecer igual bajo transformaciones de Galileo (que parece tan intuitivo que no solemos reconocer que es un postulado).

Dado que, por definici??n rotaciones deben mantener la distancia misma, pasando a un sistema de referencia diferente, deben mantener el intervalo de espacio-tiempo entre dos eventos sin cambios. Este requisito se puede utilizar para derivar una forma matem??tica expl??cita para la transformaci??n que se debe aplicar a las leyes de la f??sica (comparar con la aplicaci??n de transformaciones de Galileo a las leyes cl??sicas) al cambiar los sistemas de referencia. Estas transformaciones se denominan Transformaciones de Lorentz. Al igual que el Transformaciones de Galileo son la expresi??n matem??tica del principio de relatividad de Galileo en la mec??nica cl??sica, las transformaciones de Lorentz son la forma matem??tica de principio de la relatividad de Einstein. Las leyes de la f??sica deben permanecer igual bajo transformaciones de Lorentz. Las ecuaciones de Maxwell y La ecuaci??n de Dirac satisfacer esta propiedad, y por lo tanto son relativista leyes correctas (pero cl??sicamente incorrecta, ya que no se transforman correctamente en transformaciones de Galileo).

Con la declaraci??n de la m??trica de Minkowski, el nombre com??n de la f??rmula de la distancia indicada anteriormente, el fundamento te??rico de la relatividad especial es completa. Toda la base de la relatividad especial se puede resumir en la afirmaci??n geom??trica "cambios de sistema de referencia corresponden a rotaciones en el espacio-tiempo de Minkowski 4D, la cual se define tener la f??rmula de la distancia dada anteriormente". Las predicciones din??micas ??nicas de tallo SR de esta propiedad geom??trica del espacio-tiempo. La relatividad especial puede decirse que es la f??sica de espaciotiempo de Minkowski. En este caso del espacio-tiempo, hay seis rotaciones independientes que deben ser considerados. Tres de ellos son las rotaciones est??ndar en un plano en dos direcciones del espacio. Los otros tres son rotaciones en un plano de espacio y tiempo: Estas rotaciones se corresponden con un cambio de velocidad , y el Diagramas de Minkowski ideadas por lo describen dichas rotaciones.

Como se ha mencionado antes, se puede sustituir f??rmulas de distancia con f??rmulas de rotaci??n. En lugar de comenzar con la invariancia de la m??trica de Minkowski como propiedad fundamental del espacio-tiempo, se puede afirmar (como se hizo en la f??sica cl??sica con la relatividad de Galileo) la forma matem??tica de las transformaciones de Lorentz y requieren que las leyes f??sicas sean invariantes bajo estas transformaciones. Esto no hace referencia a la geometr??a del espacio-tiempo, sino que producir?? el mismo resultado. Este fue, de hecho, el enfoque tradicional de la SR, usado originalmente por el propio Einstein. Sin embargo, este enfoque se considera a menudo ofrecen menos perspicacia y ser m??s oneroso que el formalismo m??s natural Minkowski.

Postulado de Einstein: la constancia de la velocidad de la luz

Postulado de Einstein de que la velocidad de la luz es una constante sale como una consecuencia natural de la formulaci??n de Minkowski.

Proposici??n 1:

Cuando un objeto se desplaza a c en cierto marco de referencia, el intervalo espacio-tiempo es cero.

Prueba:

El intervalo de espacio-tiempo entre el acontecimiento de origen (0,0,0,0) y un evento (x, y, z, t) es

$s ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 - (ct) ^ 2 \,.$

La distancia recorrida por un objeto que se mueve a una velocidad v de t segundos es:

$\ Sqrt {x ^ 2 + y ^ 2 + z ^ 2} = vt \,$

dando

$s ^ 2 = (vt) ^ 2 - (ct) ^ 2 \,.$

Puesto que la velocidad v es igual a c tenemos

$s ^ 2 = (ct) ^ 2 - (ct) ^ 2 \,.$

Por lo tanto el intervalo espacio-tiempo entre los eventos de salida y llegada se da por

$s ^ 2 = 0 \,$

Proposici??n 2:

Un objeto que viaja a c en un sistema de referencia se desplaza a c en todos los marcos de referencia.

Prueba:

Deje que el objeto se mueve con una velocidad v cuando se observa desde un marco de referencia distinto. Un cambio en el marco de referencia corresponde a una rotaci??n en M. Dado que el intervalo de espacio-tiempo debe ser conservada bajo rotaci??n, el intervalo de espacio-tiempo debe ser el mismo en todos los marcos de referencia. En la proposici??n 1 demostramos que sea cero en un sistema de referencia, por lo que debe ser igual a cero en todos los dem??s sistemas de referencia. Tenemos que

$(Vt) ^ 2 - (ct) ^ 2 = 0 \,$

lo que implica

$| V | = c.$

Las trayectorias de los rayos de luz tienen un intervalo de cero espacio-tiempo, y por lo tanto todos los observadores obtendr??n el mismo valor para la velocidad de la luz. Por lo tanto, al asumir que el universo tiene cuatro dimensiones que est??n relacionadas por la f??rmula de Minkowski, la velocidad de la luz aparece como una constante, y no necesita ser asumido (postulado) que es constante como en enfoque original de Einstein de la relatividad especial.

Demoras de reloj y de varilla contracciones: m??s sobre las transformaciones de Lorentz

Otra consecuencia de la invariancia del intervalo espacio-tiempo es que van a aparecer los relojes que ir m??s lento en los objetos que se mueven con respecto al observador. Esto es muy similar a c??mo la proyecci??n 2D de una l??nea girado a la tercera dimensi??n parece que se corta. La longitud no se conserva simplemente porque estamos ignorando una de las dimensiones. Volvamos al ejemplo de John y Bill.

John observa la longitud del intervalo de espacio-tiempo de Bill como:

$s ^ 2 = (vt) ^ 2 - (ct) ^ 2 \,$

mientras que Bill no cree que ha viajado en el espacio, por lo que escribe:

$s ^ 2 = (0) ^ 2 - (CT) ^ 2 \,$

El intervalo de espacio-tiempo, s ^2, es invariante. Tiene el mismo valor para todos los observadores, no importa qui??n lo mide o c??mo se mueve en una l??nea recta. Esto significa que el intervalo espacio-tiempo de Bill es igual a la observaci??n de Juan de intervalo espacio-tiempo de Bill as??:

$(0) ^ 2 - (CT) ^ 2 = (vt) ^ 2 - (ct) ^ 2 \,$

$- (CT) ^ 2 = (vt) ^ 2 - (ct) ^ 2 \,$

por lo tanto

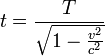$t = \ {\ sqrt {1 - \ frac {v ^ 2} {c ^ 2}}} frac {T} \,$ .

As?? pues, si Juan ve un reloj que est?? en reposo en el registro de una trama de segundo Bill, John encontrar?? que sus propias medidas de reloj entre estos mismos garrapatas un intervalo de t, llamado coordinar el tiempo, que es mayor que un segundo. Se dice que los relojes en movimiento m??s lento, en relaci??n con los de los observadores en reposo. Esto se conoce como "relativista dilataci??n del tiempo de un reloj en movimiento ". El tiempo que se mide en el marco de reposo del reloj (en el marco de Bill) se denomina el momento adecuado del reloj.

En la relatividad especial, por lo tanto, los cambios en la imagen de referencia afectan el tiempo tambi??n. El tiempo ya no es absoluta. No hay reloj universalmente correcta; el tiempo corre a diferentes velocidades para diferentes observadores.

Del mismo modo se puede demostrar que Juan tambi??n observar?? varas de medir en reposo en el planeta de Bill a ser m??s corto en la direcci??n del movimiento de sus propias varas de medir. Esto es una predicci??n conocido como "relativista longitud contracci??n de una barra en movimiento ". Si la longitud de una varilla en reposo en el planeta de Bill es X, entonces nos llaman a esta cantidad el longitud apropiada de la varilla. La longitud x de la misma barra, medida en el planeta de John, se llama coordinar longitud, y dada por

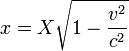$x = X \ sqrt {1 - \ frac {v ^ 2} {c ^ 2}} \,$ .

C??mo coordenadas de Bill parecen John en el instante en que se cruzan

Estas dos ecuaciones pueden ser combinados para obtener la forma general de la transformaci??n de Lorentz en una dimensi??n espacial:

$\ Begin {casos} T & = \ gamma \ dejado (t - \ frac {vx} {c ^ {2}} \ right) \\ X & = \ gamma \ left (x - vt \ right) \ end {casos }$

o equivalentemente:

$\ Begin {casos} t & = \ gamma \ left (T + \ frac {v X} {c ^ {2}} \ right) \\ x & = \ gamma \ left (X + v T \ right) \ end {casos}$

donde el Factor de Lorentz viene dada por

$\ Gamma = {1 \ over \ sqrt {1 - v ^ 2 / c ^ 2}}$

Las f??rmulas anteriores de las demoras de reloj y contracciones de longitud son casos especiales de la transformaci??n general.

Alternativamente, estas ecuaciones para la dilataci??n del tiempo y la contracci??n de la longitud (aqu?? obtenidas de la invariancia del intervalo espacio-tiempo), se pueden obtener directamente de la transformaci??n de Lorentz configurando X = 0 para la dilataci??n del tiempo, lo que significa que el reloj est?? en reposo en el sistema de Bill, o mediante el establecimiento de t = 0 para la contracci??n de la longitud, lo que significa que John debe medir las distancias a los puntos extremos de la barra en movimiento al mismo tiempo.

Una consecuencia de las transformaciones de Lorentz se modifica la la velocidad de adici??n de f??rmula:

$s = {v + u \ sobre 1+ (v / c) (u / c)}.$

Simultaneidad y reloj desincronizaci??n

La ??ltima consecuencia de espacio-tiempo de Minkowski es que los relojes parecen estar fuera de fase entre s?? a lo largo de la longitud de un objeto en movimiento. Esto significa que si un observador establece una l??nea de relojes que est??n sincronizados de modo que todos leen al mismo tiempo, a continuaci??n, otro observador que se mueve a lo largo de la l??nea a alta velocidad ver?? todos los relojes de lectura diferentes momentos. Esto significa que los observadores que se mueven uno respecto al otro ver diferentes eventos como simult??nea. Este efecto es conocido como "Fase relativista" o la "relatividad de la simultaneidad". Fase relativista es a menudo pasada por alto por los estudiantes de la relatividad especial, pero si se entiende, entonces fen??menos como la doble paradoja son m??s f??ciles de entender.

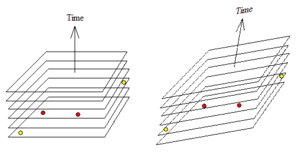
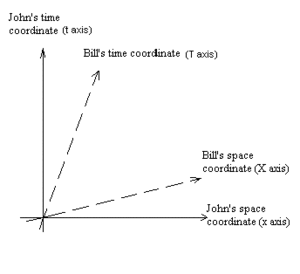
El "plano de simultaneidad" o "superficie de simultaneidad" contiene todos los eventos que suceden en el mismo instante para un observador dado. Los eventos que son simult??neos para un observador no son simult??neos para otro observador en movimiento relativo.

Los observadores tienen una serie de eventos simult??neos alrededor de ellos que consideran que compone el instante presente. La relatividad de los resultados de simultaneidad en observadores que se mueven uno respecto al otro con diferentes conjuntos de eventos en su instante presente.

El efecto neto del universo de cuatro dimensiones es que los observadores que est??n en movimiento relativo a usted parece tener las coordenadas de tiempo que se inclinan m??s en la direcci??n del movimiento, y considerar las cosas a ser simult??neos que no son simult??neos para usted. Longitudes espacial en la direcci??n de desplazamiento se acortan, porque inclinan hacia arriba y hacia abajo, en relaci??n con el eje de tiempo en la direcci??n de desplazamiento, similar a un sesgo o de cizallamiento de espacio tridimensional.

Se necesita mucho cuidado al interpretar diagramas espacio-tiempo. Diagramas de datos presente en dos dimensiones, y no se puede mostrar fielmente c??mo, por ejemplo, aparece un intervalo de espacio-tiempo de longitud cero.

La relatividad general: una mirada hacia adelante

A diferencia de las leyes del movimiento de Newton, la relatividad no se basa en postulados din??micos. No asume nada sobre el movimiento o fuerzas. M??s bien, se trata de la naturaleza fundamental del espacio-tiempo. Tiene que ver con la descripci??n geom??trica del tel??n de fondo sobre el que todos los fen??menos din??micos tienen lugar. En un sentido, por lo tanto, es una meta-teor??a, una teor??a que establece una estructura que todas las otras teor??as deben seguir. En verdad, la relatividad especial es s??lo un caso especial. Se supone que el espacio-tiempo es plano. Es decir, se asume que la estructura de espacio de Minkowski y el tensor de m??trica de Minkowski es constante a lo largo. En la relatividad general , Einstein demostr?? que esto no es cierto. La estructura del espacio-tiempo se modifica por la presencia de la materia. En concreto, la f??rmula de la distancia indicada anteriormente ya no es v??lida en general, excepto en el espacio libre de masa. Sin embargo, al igual que una superficie curva puede ser considerada plana en el l??mite infinitesimal de c??lculo, un espacio-tiempo curvo puede ser considerada plana a peque??a escala. Esto significa que la m??trica de Minkowski escrito en la forma diferencial es generalmente v??lida.

$ds ^ 2 = dx ^ 2 + dy ^ 2 + dz ^ 2 - c ^ 2 dt ^ 2 \,$

Se dice que la m??trica de Minkowski es v??lida a nivel local, pero no logra dar una medida de distancia a trav??s de grandes distancias. No es v??lida en todo el mundo. De hecho, en la relatividad general la propia m??trica mundial se vuelve dependiente de la distribuci??n de masa y var??a a trav??s del espacio. El problema central de la relatividad general es resolver el famoso Ecuaciones de campo de Einstein para una distribuci??n de masa dada y encontrar la f??rmula de la distancia que se aplica en este caso particular. Formulaci??n espaciotiempo de Minkowski fue el trampol??n conceptual a la relatividad general. Su fundamentalmente nueva perspectiva permiti?? no s??lo el desarrollo de la relatividad general, pero tambi??n en cierta medida las teor??as cu??nticas de campos .

La equivalencia masa-energ??a: la luz solar y bombas at??micas

Einstein demostr?? que la masa no es m??s que otra forma de energ??a. El equivalente de energ??a de masa en reposo m es mc ^2. Esta equivalencia implica que la masa debe ser interconvertibles con otras formas de energ??a. Este es el principio b??sico detr??s de las bombas at??micas y de la producci??n de energ??a en los reactores nucleares y las estrellas (como el Sol).

Aplicaciones

Hay una percepci??n com??n de que no es necesaria la f??sica relativista, a efectos pr??cticos, o en la vida cotidiana. Esto no es verdad. Sin efectos relativistas, el oro se ver??a plateado, en lugar de amarillo. Muchas tecnolog??as dependen cr??ticamente de la f??sica relativista:

Tubos de rayos cat??dicos,
Los aceleradores de part??culas,
Sistema de Posicionamiento Global (GPS) - aunque esto realmente requiere la teor??a completa de la relatividad general

Los postulados de la relatividad especial

Einstein desarroll?? la relatividad especial sobre la base de dos postulados:

Primero postulado - Especial principio de la relatividad - Las leyes de la f??sica son las mismas en todo marcos de referencia inerciales. En otras palabras, no hay sistemas inerciales de referencia privilegiados.
Segundo postulado - invariancia de c - La velocidad de la luz en un de vac??o es independiente del movimiento de la luz fuente.

La relatividad especial se puede derivar de estos postulados, como se hizo por Einstein en 1905. postulados de Einstein, a??n ser??n aplicables en la teor??a moderna, pero el origen de los postulados es m??s expl??cito. Se demostr?? anteriormente c??mo la existencia de una velocidad universalmente constante (la velocidad de la luz) es una consecuencia de modelar el universo como un espacio de cuatro dimensiones particular que tiene ciertas propiedades espec??ficas. El principio de la relatividad es una consecuencia de la estructura de Minkowski se conserva bajo transformaciones de Lorentz, que se postulan para ser las transformaciones f??sicas de los sistemas de referencia inerciales.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Introduction_to_special_relativity&oldid=544617470 "