Zéro

Cette page contient des caractères spéciaux ou non latins. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation…), consultez la page d’aide Unicode.

Pour les articles homonymes, voir Zéro (homonymie).

-1 — 0 — 1
Cardinal	Zéro
Ordinal	zéroième nullième[1] 0e
Préfixe grec	oudén
Préfixe latin	nihil
Adverbe	zéroièmement
Propriétés
Facteurs premiers	Aucune
Diviseurs	Tous les entiers
Système de numération	Aucun
Autres numérations
Numération romaine	(inexistant)
Numération chinoise	〇, 零, 洞
Numération indo-arabe	٠
Système binaire	0
Système octal	0
Système duodécimal	0
Système hexadécimal	0
modifier

Le zéro (de l’italien zéfiro devenu par suite zero), est un chiffre dont le nom est dérivé de l’arabe «sifr», signifiant « vide » . Ce symbole, sous forme de petit cercle, est utilisé pour « garder le rang »^[2] et marquer une position vide dans l’écriture des nombres en notation positionnelle.

Le nombre zéro est un objet mathématique permettant d’exprimer une absence comme une quantité (nulle) : c'est le nombre d'éléments de l’ensemble vide. Il délimite les nombres positifs (+) des nombres négatifs (-). Il est conçu comme le plus petit des entiers naturels. Ses propriétés arithmétiques particulières, notamment l’impossibilité de la division par zéro, impliquent parfois de traiter son cas à part. Il sépare les nombres réels en positifs et négatifs et tient lieu d’origine pour repérer des points sur la droite réelle.

Plus généralement, zéro désigne l’élément neutre pour l’addition dans la plupart des groupes abéliens et en particulier dans les anneaux, corps, espaces vectoriels et algèbres, parfois sous le nom d’élément nul. Il est aussi l'élément absorbant pour la multiplication.

Les Babyloniens ont utilisé les premiers, un peu plus de 200 ans av. J.-C., une forme de chiffre zéro à l’intérieur d’un nombre (par exemple : 304) mais jamais à droite du nombre, ni à gauche. C’est l’Inde qui, en reprenant l’héritage culturel des Grecs, perfectionne la numération. Elle n’utilise pas seulement le zéro comme notation à la manière babylonienne, mais aussi comme un nombre avec lequel opérer. Notion et notation indiennes du zéro sont ensuite empruntées par les mathématiciens arabes^[3] puis par les Européens.

Il faut noter la place particulière des Mayas, seuls arithméticiens de l’Antiquité à définir deux zéros, l’un cardinal, l’autre ordinal, comme l’illustre le verso de la plaque de Leyde^[4].

Histoire

Zéro en tant que chiffre

Il est apparu trois fois dans l’histoire des systèmes de numération élaborés par différents peuples et civilisations.

La première apparition du zéro en Mésopotamie semble remonter au III^e siècle av. J.-C., à l’époque des Séleucides. Il n’était cependant pas utilisé dans les calculs et ne servait que comme chiffre (marquage d’une position vide dans le système de numération babylonienne)^[5]. Ignoré par les Romains, il fut repris et mieux utilisé encore par les astronomes grecs.

Les inscriptions sur os et écailles (jiaguwen) découvertes dans la région de Anyang, dans l’actuelle province du Henan, à la fin du XIX^e siècle, nous apprennent que, dès les XIV^e ‑ XI^e siècles av. J.-C., les Chinois utilisaient une numération décimale de type « hybride », combinant neuf signes fixes pour les unités de 1 à 9, avec des marqueurs de position particuliers pour les dizaines, centaines, milliers et myriades. Au I^er siècle av. J.-C., en Chine antique, la numération à bâtons utilise des espaces entre les chiffres pour représenter les zéros.

La troisième fois fut celle dont nous sommes toujours héritiers, vraisemblablement dans le monde indien au III^e siècle ou même avant^[6].

En tant que nombre

Son usage moderne, à la fois comme chiffre et comme nombre, est hérité de l’invention indienne des chiffres nagari vers le V^e siècle. Le mot indien désignant le zéro était śūnya (çûnya), qui signifie « vide » « espace » ou « vacant ». Le mathématicien et astronome indien Brahmagupta est le premier à définir le zéro dans son ouvrage Brâhma Siddhânta. Ce mot, d'abord traduit en arabe par « ṣifr », ce qui signifie « vide » et « grain », a ensuite donné en français les mots chiffre et zéro (de par la traduction de sifr en l’italien zephiro, à partir duquel a été formé zevero qui est devenu zero). La graphie du zéro, d’abord un cercle, est inspirée de la représentation de la voûte céleste.

Comme l’indique l’étymologie, son introduction en Occident est consécutive à la traduction de mathématiques arabes, notamment les travaux d’al-Khwārizmī, vers le VIII^e siècle. En 976, Muhammad Ibn Ahmad, dans ses « Clés des Sciences » suggère -si aucun nombre n'apparait à la place des dizaines - d'employer un petit cercle pour « garder le rang »^[7].

Les chiffres indiens sont importés d’Espagne en Europe chrétienne aux environs de l’an mil par Gerbert d’Aurillac, devenu le pape Sylvestre II. Le zéro ne se généralise pas pour autant dans la vie courante, les chiffres indiens servant surtout à marquer les jetons d’abaque de 1 à 9.

Léonard de Pise, dit Fibonacci, a une influence déterminante. Il reste plusieurs années en Afrique du Nord en Algérie et exactement à Béjaïa ou Bougie et étudie auprès d’un professeur local. Il voyage également en Grèce, Égypte, Proche-Orient et confirme l’avis de Sylvestre II sur les avantages de la numération de position. En 1202, il publie le Liber Abaci, recueil qui rassemble pratiquement toutes les connaissances mathématiques de l’époque, et malgré son nom, apprend à calculer sans abaque.

Dans son ouvrage Zéro, la biographie d'une idée dangereuse, Charles Seife explique en quoi le zéro a permis la compréhension de nombreux concepts dans plusieurs domaines en plus des mathématiques, notamment la thermodynamique et la mécanique quantique. Entre autres, les travaux de Isaac Newton, Gottfried Wilhelm Leibniz, Richard Suiseth et Nicholas Oresme à propos des suites mathématiques, qui lient étroitement zéro avec l'infini.

Les deux zéros des Mayas

Le zéro est utilisé par les Mayas durant le I^er millénaire, comme chiffre dans leur système de numération de position, comme nombre et comme ordinal dans le calendrier, où il correspond à l’introduction des mois. En les confondant dans une transcription unique, Sylvanus Morley a masqué qu’il s’agit de deux concepts et de deux zéros différents^[4]. L’un correspond à un zéro ordinal des dates, l’autre est un zéro cardinal des durées^[8], jamais confondus dans leurs usages par les scribes^[9].

Graphies actuelles

La graphie « 0 » n’est pas la seule utilisée dans le monde ; un certain nombre d’alphabets — particulièrement ceux des langues du sous-continent indien, du sud-est asiatique et d'extrême orient — utilisent des graphies différentes…

Voici le zéro en afficheur 7 segments :

Utilisations

Il est aujourd’hui à la base de notre système de mesure de la température :

• 0 °C : température du passage de l’eau de l’état solide (glace) à l’état liquide, à une pression ambiante de 1 013 hPa ;
• 0 K : zéro absolu, température la plus basse possible (−273,15 °C), pour laquelle l’énergie rovibrationnelle et cinétique des molécules est nulle.

Il n’y a pas d’année zéro dans le calendrier grégorien. En effet, l’usage du nombre 0 en Europe est postérieur à la création de l’anno Domini par Dionysius Exiguus au VI^e siècle. Cependant pour simplifier les calculs d’éphémérides, les astronomes définissent une année 0 qui correspond à l’année -1 des historiens, l’an -1 des astronomes correspondant à l’an -2 des historiens et ainsi de suite…

C’est ainsi que le III^e millénaire et le XXI^e siècle ont commencé le 1^er janvier 2001.

Minuit peut se noter 00:00.

Les informaticiens ont l’habitude de compter à partir de 0 et non de 1. La raison en est que la numérotation d’éléments stockés de façon continue dans une zone de stockage (disque, mémoire, etc.) se fait par décalage par rapport à une adresse de début : le premier élément est celui au début de la zone (+ 0), le second élément est le suivant (+ 1), etc. Ce double standard des numérations à partir de 0 et de 1 (chaque système ayant ses avantages et inconvénients) est la source de nombreuses erreurs de programmation.

Le zéro comme notation des bases 2, 8, 10, 16…

Dans la base dix que l’on utilise, le chiffre le plus à droite indique les unités, le deuxième chiffre indique les dizaines, le troisième les centaines, le quatrième les milliers…

Le zéro joue donc un rôle particulier dans le système arithmétique positionnel, quel qu’il soit du reste.

Rappelons que l’usage de la base 10, en provenance de l’Inde, s’est imposé en France par rapport à d’autres bases, par exemple 12 et 60 qui étaient utilisées dans certaines civilisations, le système vicésimal ayant laissé des traces dans la langue française, et le système duodécimal des modes de calcul chez les Britanniques.

Lorsqu’il y a des unités résiduelles, par exemple dans trente-deux (32), le chiffre des unités (2) permet de comprendre que l’autre chiffre (3) indique les dizaines.

Si l’on a un nombre entier de dizaines (par exemple trois dizaines, trente), il n’y a pas d’unité résiduelle. Il faut donc un caractère qui permette de marquer que le 3 correspond aux dizaines, et ce caractère est le 0 ; c’est ainsi que l’on comprend que « 30 » signifie « trois dizaines ».

On aurait pu utiliser n’importe quel autre caractère, par exemple un point ; ainsi, deux-cent trois se noterait « 2.3 ».

L’utilisation d’un caractère « bouche-trou » remonte à la numération babylonienne, comme indiqué ci-dessus, mais il ne s’agit pas du concept d’« absence de quantité », il s’agit juste d’une commodité de notation. Dans la numération romaine, cet artifice n’est pas utile puisque les unités (I, V), les dizaines (X, L), les centaines (C, D) et les milliers (M) sont notés avec des caractères différents. En contrepartie, la notation de nombres supérieurs à 8 999 devient problématique et les reconnaissances de structures pour le calcul mental rapide bien plus pénibles.

Le zéro comme absence de quantité

Le fait d’exprimer l’absence de quantité par un nombre n’est pas une évidence en soi. L’absence d’un objet s’exprime par la phrase « il n’y en a pas » (ou « plus »).

Les nombres sont déjà une abstraction : on ne s’intéresse pas à la qualité d’un objet, mais juste à sa quantité, la dénombrabilité (le fait que des objets soient similaires mais distincts). Avec le zéro, on va jusqu’à nier la quantité.

Lorsque l’on additionne ou multiplie deux nombres, on a derrière l’image de regrouper deux tas d’objets semblables, deux troupeaux. Cette image ne tient plus lorsque l’on manipule le zéro.

L’invention du zéro a permis l’invention des nombres négatifs.

Propriétés arithmétiques et algébriques

En tant que nombre entier, zéro est divisible par tout autre entier relatif.

Pour tout nombre réel (ou complexe)  :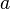

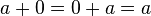• (0 est élément neutre pour l’addition)
• (0 est élément absorbant pour la multiplication)
• si 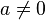alors
• 0⁰ est considéré tantôt comme égal à 1 (en algèbre et en théorie des ensembles)^[10], tantôt comme indéfini pour l'évaluation des limites en analyse (c’est une forme indéterminée du calcul des limites).
• par extension de la factorielle à l’aide de la fonction Gamma,
• 
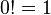
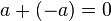
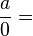• non défini (voir article division par zéro)
• non défini, en remarquant toutefois que le calcul 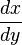lorsque les deux valeurs tendent vers zéro est la base du calcul différentiel.
• Pour tout entier n > 0, la racine n-ième de 0 est égale à 0.
• Zéro est le seul nombre qui est à la fois réel, positif, négatif et imaginaire pur.

Usage étendu de zéro en mathématiques

• Zéro est l’élément neutre dans un groupe abélien muni de la loi ou l’élément neutre pour l’addition dans un anneau.
• Un zéro d’une fonction est un point dans le domaine de définition de la fonction dont l’image par la fonction est zéro ; aussi appelé racine, surtout dans le cas d’une fonction polynôme. Voir zéro (analyse complexe).
• En géométrie, la dimension d’un point est 0.
• En topologie, la dimension topologique de l’ensemble de Cantor est 0, quoiqu’il ait une dimension de Hausdorff non nulle.
• En géométrie analytique, 0 a pour nom l’origine, notée aussi O (un cas où l’ambiguïté est bénigne).
• Le concept de « presque » impossible en probabilité. Plus généralement, le concept de presque nulle part en théorie de la mesure.
• Une fonction zéro est une fonction avec 0 comme seule valeur de sortie possible. Une fonction zéro particulière est le morphisme zéro. Une fonction zéro est l’élément neutre dans le groupe additif des fonctions.
• Zéro est l’une des trois valeurs de retour possibles de la fonction de Möbius. Si on entre un entier 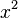ou , la fonction de Möbius retournera zéro.
• C’est un nombre de Pell.

Notes et références

Voir aussi

Fichier audio
0 en code morse
Des difficultés à utiliser ces médias ?
modifier

Numération grecque / Le zéro chez les Grecs

Articles connexes

• Alphabet morse dans lequel le chiffre 0 vaut « ----- »
• Axiomes de Peano
• Base (arithmétique)
• Brahmagupta
• Chiffre arabe
• Écriture décimale positionnelle
• Lokavibhâga
• Mathématiques
• Nombre
• Notation positionnelle
• Système décimal
• Système décimal sans zéro
• Théorème des zéros de Hilbert
• Zéro barré

Bibliographie

• Histoire universelle des chiffres, l’intelligence des hommes racontée par les nombres et le calcul. Georges Ifrah. Robert Laffont, collection Bouquins. (ISBN 978-2-221-90100-7). Tome 1, 1 042 pages, tome 2, 1 010 pages. Janvier 1994. (illustrations en couleur)
• Zéro, la biographie d’une idée dangereuse, Charles Seife, éd. Hachette, (ISBN 978-2-01-279192-3)

• Portail de l’arithmétique et de la théorie des nombres