Base (arithmétique)

Pour les articles homonymes, voir base.

En arithmétique, une base désigne la valeur dont les puissances successives interviennent dans l'écriture des nombres dans la numération N-adique, ces puissances définissant l'ordre de grandeur de chacune des positions occupées par les chiffres composant tout nombre. Par commodité, on utilise usuellement, pour les bases entières à partir de deux, un nombre de chiffres égal à la base. En effet, l'écriture d'un nombre en base N à l'aide de N chiffres allant de 0 à N-1 correspond à son développement en base N.

Bases courantes

Certaines bases sont couramment employées :

la base deux (système binaire), en électronique numérique et informatique,
la base trois (système trinaire), dans les mêmes domaines, bien que moins fréquemment,
la base huit (système octal), en informatique, davantage à l'échelle humaine que la base deux, aujourd'hui abandonnée au profit de la base seize. Elle a été utilisée par les yuki,
la base neuf (système nonaire), davantage à l'échelle humaine que la base 3,
la base dix (système décimal), la plus commune, aujourd'hui la référence dans le domaine des sciences,
la base douze (système duodécimal), de manière embryonnaire, a été utilisée par les Égyptiens pour le compte en heures et mois,
la base seize (système hexadécimal), en informatique, facilitant les conversions en base 2 en regroupant des chiffres binaires, 16 étant une puissance de 2,
la base vingt (système vigésimal) a été utilisée par les Mayas et les Aztèques, ainsi que de manière alternative en France (dont on garde en l'héritage pour quatre-vingt)
la base soixante (système sexagésimal), dans la mesure du temps et des angles, a été utilisée par les Sumériens, les Akkadiens, puis les Babyloniens. (voir Numération babylonienne)
la base cent cinquante ou base indienne, utilisée notamment dans la table astronomique appelée Table indienne d’al-Khawarizmi

De nombreuses bases sont, et ont été, aussi utilisées par différents peuples ; consulter Numération pour plus de détails.

Bien que peu utilisée, la base trente a l'intérêt d'exprimer simplement le résultat de la majorité des petites fractions (à dénominateurs de la forme 2ⁿ.3^p.5^q), et les factorielles. De plus, à la différence de la base 60, elle peut être représentée à l'aide des 10 chiffres courants et des 20 premières lettres de l'alphabet.

Pour des applications spécifiques, l'informatique peut utiliser des base ad hoc : pour un entier représenté par une chaîne d'octets, on peut considérer un octet comme un chiffre en base 256 ; on peut voir un identificateur comme un nombre en base 40 ; pour des applications décimales, on peut avoir avantage à utiliser une base 1000.

Symboles utilisés

Pour les bases jusqu'à 10 inclus, on utilise les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.

Au-delà, on utilise les lettres. Par exemple, pour la base 16, les symboles utilisés sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

L'usage du zéro positionnel est une convention pratique et élégante, mais non nécessaire pour représenter les entiers naturels, comme l'illustre le système décimal sans zéro. Il est, par contre, indispensable pour généraliser l'écriture positionnelle aux nombres fractionnaires.

Notations courantes

Pour n'importe quelle base, on a l'habitude de l'indiquer en indice du nombre. Par exemple $100111_2$ pour le nombre 100111 en base 2, ou encore $172_8$ pour le nombre 172 en base 8.

En plus de cette notation, il en existe d'autres, notamment employées en informatique.

Base 8 : on peut indiquer le nombre avec un zéro au début. Par exemple 0157 pour $157_8$ .
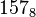Base 16 : on peut indiquer de diverses manières qu'un nombre est en hexadécimal (voir tableau ci-dessous). Une autre écriture courante est l'ajout du suffixe "h" à la fin du nombre, ce qui avec notre exemple donne AE4Fh.

Préfixe	Exemple	Langages
0x	`0xAE4F`	C, C++, Java
$	`$AE4F`	Pascal
&h	`&hAE4F`	Basic
#	`#AE4F`	HTML

Conversion d'une base à une autre

Un nombre dans une base n donnée s'écrit sous la forme d'additions des puissances successives de cette base.

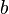Le nombre $c_n...c_2c_1c_0$ en base $b$ , constitué des chiffres 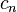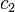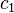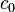$c_n$ , ..., $c_2$ , $c_1$ , $c_0$ , peut aussi s'écrire sous la forme 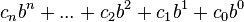$c_n b^n + ... + c_2 b^2 + c_1 b^1 + c_0 b^0$ , c'est-à-dire un polynôme dont les coefficients sont les chiffres et l'inconnue est la base.

Lorsqu'on veut passer d'une base à une autre, on utilisera 2 méthodes (algorithmes) suivant que l'on sait calculer dans la base de départ ou dans la base d'arrivée.

Si on sait calculer dans la base de départ, des divisions entières successives par la base donneront en reste les chiffres du résultat, en commençant par les unités. Plus précisément :

q_0 :=n

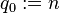(le nombre à convertir) ;

i:=0

;

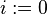tant que

q_i >0

faire

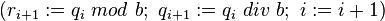
(r_{i+1}:= q_i\ mod\ b ;\ q_{i+1}:= q_i\ div\ b ;\ i := i+1 )

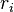les $r_i$ sont les chiffres du nombre converti, en partant des unités.

Si on sait calculer dans la base d'arrivée, on évalue le polynôme (en représentant les coefficients et la base de départ dans la base d'arrivée). La méthode de Horner est généralement utilisée :

v :=c_n

;

i:=n

;

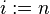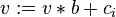pour i:=n-1 a 0 faire

v := v *b +c_i

;

v est le nombre dans la base d'arrivée.

Si on ne sait calculer ni dans la base de départ ni dans celle d'arrivée, on passe par une base intermédiaire où l'on sait calculer.

Si la base d'arrivée est une puissance de la base de départ (exemple : de la base 2 à la base 16), on peut convertir groupes de chiffres à chiffre, localement et directement.

Systèmes balancés

Un système numérique de base 2N ou 2N+1 peut également être doté des 2N+1 chiffres signés N, ..., 2, 1, 0, 1, 2, ..., N. On parle alors de système balancé ou symétrique.

Bases non standard

On peut également employer des bases :

négatives, pour lesquelles les nombres sont signés mais pas les chiffres ;
non-entières, on parle alors de bêta-numération (la base d'or en est un exemple) ;
imaginaires (par exemple, le système quater-imaginaire ou la base 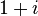$1+i\,$ , dans laquelle tout nombre complexe peut se développer, est une généralisation aux complexes du développement binaire) ;
mixtes (en), pour lesquels la base varie d'une position à une autre. Par exemple dans la notation 11₂16₁₆17₈, le terme 17₈ correspond à la notation de 1×8+7 = 15 en base 8, 16₁₆ à 1×16+6 en base 16 = 22 et 11₂à 1×2+1 = 3 en base 2 ; au total, le nombre représenté est donc égal à 15+(22×8)+(3×16×8) = 575

Un usage courant de notation en base mixte est celui des dates notamment dans le format ISO 8601 tel qu'il est par exemple utilisé au Canada : 2014-08-29 est un simplification de la notation 201408₁₂29₃₀ qui indique que le nombre de jours est transcrit selon une base trigésimale (env. 30 jours par mois) et les mois selon une base duodécimale.

Quelques propriétés

Zéro s'écrit 0 dans toutes les bases.
De la même manière, le nombre un s'écrit 1 dans toutes les bases, puisque quelle que soit la base, $base^0$ égale 1.
L'égalité « 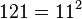$121 = 11^2$ » est vraie dans toutes les bases naturelles strictement supérieures à 2.
En base dix, un nombre est pair s'il se termine par un multiple de 2, c'est-à-dire 0, 2, 4, 6 ou 8 ; en base 2, il est pair s'il se termine par 0. Inversement, en base dix, un nombre est impair s'il se termine par un chiffre impair, soit 1, 3, 5, 7 ou 9, et en base deux s'il se termine par 1.
L'alternance des chiffres 0 et 1 en binaire se fait avec les chiffres 5 ou A en hexadécimal.

555₁₆ = 010101010101₂

AAA₁₆ = 101010101010₂

Un nombre s'écrivant de la même façon dans deux bases naturelles différentes est plus grand dans la plus grande base.

57₁₆ (=87₁₀) > 57₁₀ > 57₈ (=47₁₀)

De même, un grand nombre aura besoin de moins de chiffres pour s'écrire dans une grande base naturelle que dans une petite.

F4240₁₆ (5 chiffres) = 1 000 000₁₀ (7 chiffres) = 1111 0100 0010 0100 0000₂ (20 chiffres)

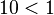$10 < 1$ en base n, avec n appartenant à l'intervalle ]0;1[, 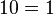$10 = 1$ en base 1, et 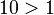$10 > 1$ en base n, avec n appartenant à l'intervalle ]1;+∞[.
la base s'écrit 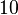$10$ dans toutes les bases. 10₂ = 2, 10₁₆ = 16, 10₆₀ = 60
En base N, un nombre est divisible par N-1 (ou un diviseur de N-1) si la somme de ses chiffres est divisible par N-1 (ou un diviseur de N-1) (exemple connu: la divisibilité par 3 ou par 9 en base 10).

Culture

Le nombre π est irrationnel et donc, quelle que soit la base naturelle utilisée, les chiffres après la virgule sont infinis et ne présentent pas de répétition, au contraire des fractions comme 1/7 = 0.142857 142857...
Boby Lapointe avait imaginé un usage comique du système hexadécimal, qu'il avait baptisé Système bibi-binaire. Ce système présentait l'avantage de rendre les nombres binaires faciles à prononcer et à mémoriser.
La RFC 1924 propose la base 85 pour la notation des adresses IPv6, mais ce n'est qu'un poisson d'avril.
Dans le jeu vidéo Portal, lors du combat final, GlaDOS annonce que 2+2 font 10, avant de se rattraper en complétant avec "En base 4, je vais bien !".
Les Shadoks comptent en quaternaire.

Articles connexes

Numération, système de numération
Base d'or (base φ)
Système négabinaire

Portail de l’arithmétique et de la théorie des nombres

This article is issued from Wikipédia - version of the Tuesday, October 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.