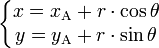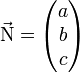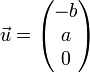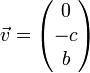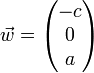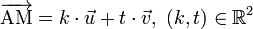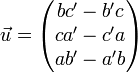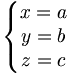Géométrie analytique
La géométrie analytique est une approche de la géométrie dans laquelle les objets sont représentés par des équations ou des inéquations. Elle est fondamentale pour la physique et l'infographie.
En géométrie analytique, le choix d'un repère est indispensable. Tous les objets seront décrits relativement à ce repère, à l'aide de coordonnées.
Histoire
Analyse en géométrie
Le terme de géométrie analytique, par opposition à la géométrie synthétique, se réfère aux méthodes d'analyse et synthèse pratiquées par les géomètres grecs. Elle en est progressivement venue à se confondre avec sa méthode privilégiée, la méthode des coordonnées.
Dans les mathématiques grecques, l'analyse consiste à partir de l'objet cherché, en supposant son existence, de manière à établir ses propriétés. Il faut poursuivre dans cette voie jusqu'à produire assez de propriétés pour caractériser l'objet. La situation peut être renversée en ne faisant plus l'hypothèse d'existence et en introduisant effectivement l'objet par le biais des propriétés caractéristiques : c'est la phase de synthèse, qui doit aboutir à la preuve d'existence.
La difficulté pratique qui a limité les progrès des géomètres est le manque d'un formalisme adapté à la description des relations entre grandeurs géométriques. François Viète, à la fin du XVIe siècle unifie le calcul sur les nombres et le calcul sur les grandeurs géométriques à travers un outil précieux, le calcul littéral. Le principe de la réduction au calcul algébrique est posé, il manque encore une méthode systématique pour l'exploiter.
Méthode des coordonnées
Marino Ghetadi, puis René Descartes proposent de résoudre les problèmes de géométrie par le recours systématique au calcul algébrique. Dans sa Géométrie de 1637, le philosophe en formule le principe. Il s'agit de représenter grandeurs connues et inconnues par des lettres, et de trouver autant de relations entre grandeurs connues et inconnues qu'il y a d'inconnues au problème. On y reconnaît bien une démarche analytique, conduisant à des systèmes d'équations qu'il s'agit de réduire à une seule équation. Descartes donne des interprétations des cas sur- ou sous-déterminés. Ses manipulations, cependant, se limitent aux équations algébriques, qu'il classe par degré, et ne peuvent être appliquées aux courbes qu'il qualifie de mécaniques (aujourd'hui dites transcendantes).
Pierre de Fermat est le premier à faire, à la même époque, un usage systématique des coordonnées proprement dites pour résoudre les problèmes de lieux géométriques. Il fait intervenir notamment les premières équations de droites, paraboles ou hyperboles. Il présente ces idées dans Ad locus planos et solidos isagoge, en 1636, texte publié après sa mort.
Dans les notations de Descartes, contrairement à Fermat, les constantes sont continuellement notées a, b, c, d, ... et les variables x, y, z. Il s'oppose en cela à la tradition de l'époque et un lecteur d'aujourd'hui s'en trouve moins dérouté.
Géométrie analytique plane
Le plan affine est muni d'un repère 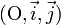 ; x désigne l'abscisse d'un point, et y l'ordonnée de ce point.
; x désigne l'abscisse d'un point, et y l'ordonnée de ce point.
Droite
Une droite affine (c'est-à-dire une droite au sens habituel, un ensemble de points) est caractérisée par une équation du premier degré à deux inconnues. C'est-à-dire que tout point M de coordonnées x et y appartient à la droite si et seulement si ses coordonnées vérifient l'équation :
- ax + by + c = 0 (1)
Si c est nul, alors la droite passe par O, l'origine du repère. Si deux droites sont parallèles, alors leurs coefficients a et b sont proportionnels. Si b n'est pas nul, l'équation (1) est équivalente à :
- y = a′·x + b′ (2)
a′ = - a/b est appelé le coefficient directeur ou la pente de la droite dans un repère orthonormal, et b′ = - c/b est appelé ordonnée à l'origine (offset ou intercept en anglais) ; deux droites parallèles ont le même coefficient directeur. Avec cette forme là, on voit aisément que la droite passe par le point (0,b′), qui est également appelé ordonnée à l'origine (le terme désigne donc à la fois le point et l'ordonnée de ce point). Si a est nul, on a une droite horizontale
- y = b′
passant par le point (0,b′). Si b est nul, on a une droite verticale
- x = - c/a
passant par le point (- c/a, 0).
Pour tracer une droite à partir de son équation, il suffit de connaître deux points. Le plus simple est de prendre l'intersection avec les axes, c'est-à-dire de considérer successivement x = 0 et y = 0 (sauf si la droite est parallèle à un axe, auquel cas le tracé est trivial). On peut aussi prendre l'ordonnée à l'origine et un point « éloigné » (c'est-à-dire au bord de la figure tracée sur le papier, par exemple considérer x = 10 si l'on va jusqu'à 10), ou encore deux points éloignés (un à chaque bord de la figure) ; en effet, plus les points sont éloignés, plus le tracé de la droite est précis.
Une droite vectorielle (c'est-à-dire un ensemble de vecteurs colinéaires) est représentée simplement par une équation de droite avec c nul :
- au1 + bu2 = 0
où u1 et u2 sont les coordonnées des vecteurs. On en déduit que pour une droite affine ou vectorielle, le vecteur de coordonnées
est un vecteur directeur de la droite. Si le repère est orthonormé, d'après une propriété du produit scalaire, le vecteur
est un vecteur normal à la droite.
Quel que soit le repère, si A(xA,yA) est un point de la droite et 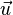 un vecteur directeur, alors pour tout point M(xM,yM) de la droite, on a
un vecteur directeur, alors pour tout point M(xM,yM) de la droite, on a
puisque 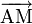 est colinéaire à
est colinéaire à 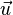 . Ceci nous donne une équation paramétrique de la droite :
. Ceci nous donne une équation paramétrique de la droite :
qui peut s'écrire
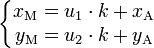 (2)
(2)
en éliminant le paramètre k, on retrouve une équation de la forme (1).
Point
Un point est représenté par un système de deux équations du premier degré à deux inconnues :
ce qui est logique puisque, un point étant l'intersection de deux droites non-parallèles, ses coordonnées doivent vérifier les équations des deux droites : la réduction de ce système d'équations donne la forme ci-dessus. Ceci est bien évidemment la représentation du point (a, b).
Demi-plan
Un demi-plan est représenté par une inéquation du premier degré à deux inconnues :
- ax + by + c > 0
si l'on remplace le signe > par un signe =, on obtient l'équation de la droite qui délimite le demi-plan ; si l'on remplace le signe > par le signe < (ou si l'on inverse les signe des coefficients), on obtient le demi-plan complémentaire.
Intersection de droites
Le plan est rapporté à un repère. Une droite (non verticale) peut être définie par une équation :
- y = ax + b.
Si on considère 2 droites définies par les équations y = ax + b et y = a'x + b', on peut savoir s'il y a une intersection ou non grâce à l'un des 3 cas suivant :
- si a = a' et b ≠ b', alors les droites sont parallèles et il n'y a pas d'intersection ;
- si a = a' et b = b', alors les 2 droites sont confondues et il y a donc une infinité de points d'intersection ;
- si a ≠ a', quels que soient b et b', il y a forcément un point d'intersection ; on obtient comme coordonnées du point d'intersection :
-
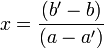 et
et -
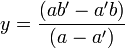 .
.
La démonstration se fait grâce à la résolution d'un système de deux équations à deux inconnues : y = ax + b et y = a'x + b'.
Demi-droite
Une demi-droite est caractérisée par une équation et une inéquation :
avec au moins a ≠a′ ou b ≠b′. Une demi-droite est en effet l'intersection d'une droite et d'un demi-plan délimité par une droite non parallèle à la première. La résolution du système obtenu en remplaçant le signe « > » par un signe « = » donne les coordonnées du point extrémité de la demi-droite, c'est-à-dire les coordonnées du point A d'une demi-droite [AB). Si a′ est non-nul, on peut se ramener à un système du type :
(les deux systèmes représentant des demi-droites complémentaires), sinon à un système du type :
Avec une équation paramétrique, cela revient à l'équation (2) en rajoutant la condition k > 0 ou k < 0.
Cercle et disque
Le cercle de centre A et de rayon r est l'ensemble des points situés à une distance r de A. Son équation est donc :
que l'on peut écrire :
Cette forme porte le nom « d'équation cartésienne du cercle ». Son équation paramétrique est :
où θ est un réel, qui peut être pris sur un intervalle de largeur 2π ; on prend en général ]-π, π] ou [0, 2π[. L'équation du disque s'obtient en remplaçant le signe « égal » par un signe « inférieur ou égal ».
Géométrie analytique dans l'espace
L'espace affine est muni d'un repère 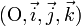 ; x désigne l'abscisse d'un point, y l'ordonnée et z la cote.
; x désigne l'abscisse d'un point, y l'ordonnée et z la cote.
Plan
Un plan affine (c'est-à-dire un plan au sens habituel en géométrie, composé de points) est représenté par une équation du premier degré à trois inconnues :
- ax + by + cz + d = 0 (3)
Si le repère de l'espace est orthonormal, le vecteur
est un vecteur normal au plan
Si deux plans sont parallèles entre eux, alors ils ont des vecteurs normaux proportionnels (colinéaires), alors leurs coefficients a, b et c sont proportionnels. Si d est nul, alors le plan passe par l'origine O. Si c est non nul, l'équation peut s'écrire :
- z = a′·x + b′·y + c′
avec a′ = - a/c, b′ = - b/c et c′ = - d/c. Si c est nul, alors on a un plan vertical.
Un plan vectoriel (c'est-à-dire un ensemble de vecteurs coplanaires) est représenté par une équation
- au1 + bu2 + cu3 = 0
où u1, u2 et u3 sont les composantes d'un vecteur. Les vecteurs suivants sont des vecteurs du plan vectoriel, et si au moins deux coefficients de l'équation du plan sont non nuls, deux de ces vecteurs forment une base du plan :
(la base obtenue n'est a priori pas orthonormée). Ces vecteurs forment aussi des vecteurs d'un plan affine dont l'équation a les mêmes coefficients a, b et c que l'équation du plan vectoriel.
Si deux des coefficients sont nuls, alors l'équation se réduit à l'une des trois formes suivantes :
- u1 = 0, qui représente le plan vectoriel
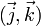 ;
; - u2 = 0, qui représente le plan vectoriel
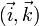 ;
; - u3 = 0, qui représente le plan vectoriel
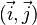 .
.
De même,
- ax + d = 0 représente un plan affine parallèle à
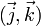 , dont l'équation peut s'écrire x = - d/a
, dont l'équation peut s'écrire x = - d/a - by + d = 0 représente un plan affine parallèle à
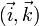 , dont l'équation peut s'écrire y = - d/b
, dont l'équation peut s'écrire y = - d/b - cz + d = 0 représente un plan affine parallèle à
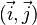 , dont l'équation peut s'écrire z = - d/c.
, dont l'équation peut s'écrire z = - d/c.
Quel que soit le repère, si le plan passe par un point A(xA, yA, zA) et est muni d'une base quelconque 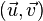 , alors pour tout point M(xM, yM, zM), on a
, alors pour tout point M(xM, yM, zM), on a
puisque 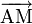 ,
, 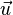 et
et 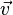 sont coplanaires. Ceci conduit à l'équation paramétrique
sont coplanaires. Ceci conduit à l'équation paramétrique
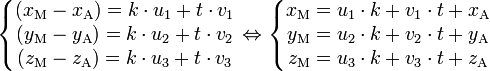 (4)
(4)
Droite
Une droite étant l'intersection de deux plans non-parallèles, elle est décrite par un système de deux équations du premier degré à trois inconnues :
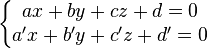 (5)
(5)
La droite est contenue dans les deux plans, elle est donc orthogonale aux vecteurs normaux 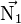 et
et 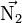 des deux plans. Le produit vectoriel
des deux plans. Le produit vectoriel 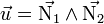 des vecteurs normaux fournit donc un vecteur directeur de la droite. Si le repère est orthonormé direct, le vecteur
des vecteurs normaux fournit donc un vecteur directeur de la droite. Si le repère est orthonormé direct, le vecteur 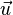 a pour composantes :
a pour composantes :
Si par ailleurs on connaît un point A(xA, yA, zA) et un vecteur directeur 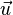 de la droite, alors si M(xM, yM, zM) est un point de la droite, il vérifie :
de la droite, alors si M(xM, yM, zM) est un point de la droite, il vérifie :
puisque 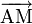 et
et 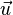 sont colinéaires. On obtient donc l'équation paramétrique :
sont colinéaires. On obtient donc l'équation paramétrique :
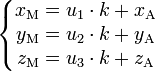 (6)
(6)
Point
Un point étant l'intersection de trois plans, il est décrit par un système de trois équations du premier degré à trois inconnues :
Le point étant l'intersection de trois plans concourants, ses coordonnées doivent vérifier les trois équations ; la réduction de ce système donne la forme ci-dessus. Ce système d'équations représente bien sûr le point (a, b, c).
Voir aussi
- Géométrie euclidienne
- Géométrie dans l'espace
- Géométrie vectorielle
- Repérage dans le plan et dans l'espace
- Volumes de révolution (cône Cône (géométrie), cylindre, sphère, ellipsoïde, paraboloïde)
- Propriétés métriques des droites et plans
Références
- Jean Dhombres et al., Mathématiques au fil des âges [détail des éditions] Textes choisis et commentés illustrant notamment la naissance de la géométrie analytique
- Portail de la géométrie
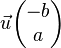
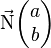
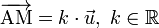
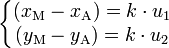
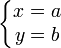
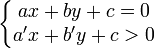
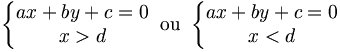

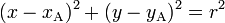
![y = y_\mathrm{A} \pm \sqrt{r^2 - (x-x_\mathrm{A})^2},\ x \in [x_\mathrm{A}-r,x_\mathrm{A}+r]](../i/m/eda1659daff6cfa884fae99100c16160.png)