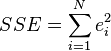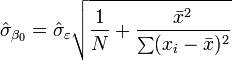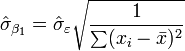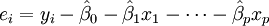L'analyse de r??gression

Saviez-vous ...

Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

L'analyse de r??gression est une technique utilis??e pour la mod??lisation et l'analyse de donn??es num??riques comprenant des valeurs d'une variable d??pendante (variable de r??ponse) et d'un ou plusieurs variables ind??pendantes (variables explicatives). La variable d??pendante dans l'??quation de r??gression est mod??lis??e comme une fonction des variables ind??pendantes, correspondant param??tres (??constantes??), et un terme d'erreur. Le terme d'erreur est trait?? comme une variable al??atoire . Il repr??sente la variation inexpliqu??e de la variable d??pendante. Les param??tres sont estim??s de fa??on ?? donner un "meilleur ajustement" des donn??es. La plupart du temps le meilleur ajustement est ??valu??e en utilisant le moindres carr??s m??thode, mais d'autres crit??res ont ??galement ??t?? utilis??s.

La mod??lisation des donn??es peut ??tre utilis?? sans qu'il y ait des connaissances sur les processus sous-jacents qui ont g??n??r?? les donn??es; dans ce cas, le mod??le est un mod??le empirique. En outre, dans la connaissance de la mod??lisation de la distribution de probabilit?? des erreurs ne est pas n??cessaire. L'analyse de r??gression n??cessite la formulation d'hypoth??ses concernant la distribution de probabilit?? des erreurs. Les tests statistiques sont effectu??s sur la base de ces hypoth??ses. En analyse de r??gression du terme ??mod??le?? englobe ?? la fois la fonction utilis??e pour mod??liser les donn??es et les hypoth??ses concernant les distributions de probabilit??.

La r??gression peut ??tre utilis?? pour pr??diction (y compris pr??vision des donn??es de s??ries chronologiques), inf??rence, tests d'hypoth??ses, et la mod??lisation des relations causales. Ces utilisations de la r??gression se appuient fortement sur les hypoth??ses sous-jacentes ??tant satisfaits. L'analyse de r??gression a ??t?? critiqu??e comme ??tant mal utilis?? ?? ces fins dans de nombreux cas o?? les hypoth??ses appropri??es ne peuvent pas ??tre v??rifi??es ?? tenir. Un facteur qui contribue ?? la mauvaise utilisation de la r??gression est qu'il peut prendre beaucoup plus de comp??tence pour critiquer un mod??le que pour se adapter ?? un mod??le.

Histoire de l'analyse de r??gression

La premi??re forme de r??gression ??tait la m??thode des moindres carr??s , qui a ??t?? publi?? par Legendre en 1805, et par Gauss en 1809. Le terme "moindres carr??s" est du mandat de Legendre, moindres carr??s. Cependant, Gauss a affirm?? qu'il avait connu la m??thode depuis 1795.

Legendre et Gauss fois appliqu?? la m??thode au probl??me de d??terminer, ?? partir d'observations astronomiques, les orbites des corps sur le soleil. Euler avaient travaill?? sur le m??me probl??me (1748) sans succ??s. Gauss publi?? un autre d??veloppement de la th??orie des moindres carr??s en 1821, dont une version de la Th??or??me de Gauss-Markov.

Le terme ??r??gression?? a ??t?? invent?? dans le XIXe si??cle pour d??crire un ph??nom??ne biologique, ?? savoir que la descendance d'individus exceptionnels ont tendance en moyenne ?? ??tre moins exceptionnelle que leurs parents et plus comme leurs anc??tres plus ??loign??s. Francis Galton, cousin de Charles Darwin , a ??tudi?? ce ph??nom??ne et appliqu?? le terme un peu trompeuse " r??gression vers la m??diocrit?? ???? elle. Pour Galton, la r??gression ne avaient que cette signification biologique, mais son travail a ensuite ??t?? ??tendu par Udny Yule et Karl Pearson ?? un contexte statistique plus g??n??rale. Aujourd'hui, le terme ??r??gression?? est souvent synonyme de "moindres carr??s ajustement de courbe ".

Hypoth??ses sous-jacentes

L'??chantillon doit ??tre repr??sentatif de la population pour la pr??diction d'inf??rence.
La variable d??pendante est sujette ?? l'erreur. Cette erreur est suppos?? ??tre une variable al??atoire , avec une moyenne de z??ro. L'erreur syst??matique peut ??tre pr??sent, mais son traitement est hors de la port??e de l'analyse de r??gression.
La variable ind??pendante est sans erreur. Si ce ne est pas le cas, la mod??lisation devrait ??tre fait en utilisant Erreurs dans les variables de techniques de mod??le.
Les pr??dicteurs doivent ??tre lin??airement ind??pendants, ce est ?? dire qu'il ne doit pas ??tre possible d'exprimer toute pr??dicteur comme une combinaison lin??aire des autres. Voir Multicollinear.
Les erreurs sont non corr??l??s, ce est le matrice de variance-covariance des erreurs est diagonale et chaque ??l??ment non nul est la variance de l'erreur.
La variance de l'erreur est constante ( homosc??dasticit??). Dans le cas contraire, les poids doivent ??tre utilis??s.
Les erreurs suivent une distribution normale . Sinon, le mod??le lin??aire g??n??ralis?? doit ??tre utilis??.

R??gression lin??aire

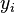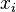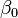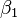Dans la r??gression lin??aire, la sp??cification du mod??le est que la variable d??pendante, $y_i$ est un combinaison lin??aire des param??tres (mais ne est pas n??cessairement lin??aire dans les variables ind??pendantes). Par exemple, dans la r??gression lin??aire simple, il est une variable ind??pendante, $x_i$ , Et les deux param??tres, $\ Beta_0$ et $\ Beta_1$ :

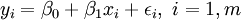
ligne droite: $y_i = \ beta_0 + \ beta_1 x_i + \ epsilon_i, \ i = 1, m \!$

Dans la r??gression lin??aire multiple, il existe plusieurs variables ind??pendantes ou des fonctions de variables ind??pendantes. Par exemple, l'ajout d'un terme x _i ² ?? la r??gression pr??c??dente donne:

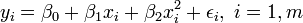
parabole: $y_i = \ beta_0 + \ beta_1 x_i + \ beta_2 x_i ^ 2 + \ epsilon_i, \ i = 1, m \!$

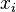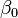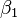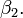
Ce est toujours la r??gression lin??aire bien que l'expression sur le c??t?? droit est quadratique de la variable ind??pendante $x_i$ Il est lin??aire dans les param??tres $\ Beta_0$ , $\ Beta_1$ et $\ Beta_2.$

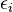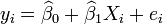Dans les deux cas, $\ Epsilon_i$ est un terme d'erreur et l'indice $Je$ un index d'observation particuli??re. Compte tenu d'un ??chantillon al??atoire de la population, nous estimons les param??tres de la population et obtenons le mod??le de r??gression lin??aire ??chantillon: $y_i = \ widehat {\ beta} _0 + \ widehat {\ beta} _1 X_i + E_I$ Le terme 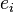$E_I$ est le r??sidu, 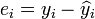$E_I = y_i - \ widehat {y} _i$ . Une m??thode d'estimation est ordinaire [moindres carr??s]. Ce proc??d?? obtient des estimations de param??tres qui minimisent la somme du carr?? r??sidus, ESS:

$SSE = \ sum_ {i = 1} ^ {} N E_I ^ 2$

Minimisation de cette fonction se traduit par un ensemble de ??quations normales, un ensemble d'??quations lin??aires simultan??es ?? des param??tres, qui sont r??solus pour donner les estimateurs de param??tres, 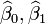$\ Widehat {\ beta} _0, \ widehat {\ beta} _1$ . Voir coefficients de r??gression pour les propri??t??s statistiques de ces estimateurs.

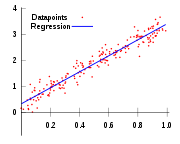
Illustration de la r??gression lin??aire sur un ensemble de donn??es (points rouges).

Dans le cas de la r??gression simple, les formules pour les estimations des moindres carr??s sont

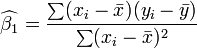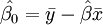
$\ Widehat {\ beta_1} = \ frac {\ sum (x_i- \ bar {x}) (y_i- \ bar {y})} {\ sum (x_i- \ bar {x}) ^ 2}$ et $\ Hat {\ beta_0} = \ bar {y} - \ hat {\ beta} \ bar {x}$

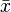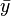o?? $\ Bar {x}$ est la moyenne (moyenne) de la $x$ valeurs et $\ Bar {y}$ est la moyenne de la 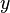$y$ des valeurs. Voir lin??aires des moindres carr??s (droite montage) pour une d??rivation de ces formules et un exemple num??rique. Dans l'hypoth??se o?? le terme d'erreur de la population a une variance constante, l'estimation de variance qui est donn??e par: $\ Hat {\ sigma _ {\ varepsilon}} = \ sqrt {\ frac {} {SSE N-2}}$ Ceci est appel?? le erreur quadratique moyenne (RMSE) de la r??gression. Le erreurs standard des estimations des param??tres sont donn??s par

$\ Hat \ sigma _ {\ beta_0} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {N} + \ frac {\ bar {x} ^ 2} {\ sum (x_i- \ bar x) ^ 2}}$

$\ Hat \ sigma _ {\ beta_1} = \ hat \ sigma _ {\ varepsilon} \ sqrt {\ frac {1} {\ sum (x_i- \ bar x) ^ 2}}$

Dans l'hypoth??se en outre que le terme d'erreur de la population est normalement distribu??, le chercheur peut utiliser ces erreurs-types estim??es pour cr??er des intervalles de confiance et effectuer des tests d'hypoth??ses sur les param??tres de la population.

Mod??le de donn??es lin??aire g??n??ral

Dans le mod??le plus g??n??ral de r??gression multiple, y sont des variables ind??pendantes p: 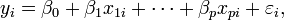$y_i = \ beta_0 + \ beta_1 x_ {} 1i + \ cdots + \ beta_p x_ {pi} + \ varepsilon_i,$ Les estimations des param??tres moindres carr??s sont obtenues par p ??quations normales. Le r??sidu peut ??tre ??crite comme

$E_I = y_i - \ hat \ beta_0 - \ hat \ beta_1 x_1 - \ cdots - \ hat \ beta_p x_p$

Le ??quations normales sont

$\ Sum_ {i = 1} ^ {N} \ sum_ {k = 1} ^ {p} {ij} X_ X_ {ik} \ hat \ beta_k = \ sum_ {i = 1} ^ {} N X_ {ij} y_i, \ j = 1, p \,$

En notation matricielle, les ??quations normales sont ??crites en tant que

$\ Mathbf {\ left (X ^ TX \ right) \ hat \ boldsymbol \ beta = X ^ Ty}$

Pour voir un exemple num??rique r??gression lin??aire (exemple)

Les diagnostics de r??gression

Une fois qu'un mod??le de r??gression a ??t?? construit, il est important de confirmer la qualit?? de l'ajustement du mod??le et de la signification statistique des param??tres estim??s. Contr??les couramment utilis??s de qualit?? de l'ajustement incluent le R-carr??, les analyses du motif de r??sidus et tests d'hypoth??ses. La signification statistique est v??rifi??e par un F-test de l'ajustement global, suivie par des tests t de param??tres individuels.

Les interpr??tations de ces tests de diagnostic reposent lourdement sur les hypoth??ses du mod??le. Bien que l'examen des r??sidus peut ??tre utilis?? pour invalider un mod??le, les r??sultats d'un test t ou Test F sont de sens que si les hypoth??ses de mod??lisation sont satisfaits.

Le terme d'erreur ne peut pas avoir une distribution normale. Voir mod??le lin??aire g??n??ralis??.
La variable de r??ponse peut ??tre discontinue. Pour binaire (z??ro ou un) des variables, il ya la probit et mod??le logit. Le mod??le probit multivari??e permet d'estimer conjointement la relation entre plusieurs variables d??pendantes binaires et certaines variables ind??pendantes. Pour variables cat??goriques ayant plus de deux valeurs, il ya la logit multinomial. Pour variables ordinales ayant plus de deux valeurs, il existe le logit ordonn?? et mod??les de probit ordonn??. Une alternative ?? ces proc??dures est la r??gression lin??aire bas??e sur des corr??lations polychoriques ou polyserial entre les variables cat??gorielles. Ces proc??dures diff??rent dans les hypoth??ses formul??es au sujet de la distribution des variables dans la population. Si la variable est positive par de faibles valeurs et repr??sente la r??p??tition de la survenance d'un ??v??nement, compter des mod??les comme la La r??gression de Poisson ou de la mod??le binomial n??gatif peut ??tre utilis??

Interpolation et extrapolation

Des mod??les de r??gression pr??dire une valeur de la 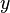$y$ les valeurs des variables donn??es connues de la $x$ Variables. Si la pr??diction doit ??tre effectu??e dans la plage de valeurs de la $x$ variables utilis??es pour construire le mod??le ce est connu comme l'interpolation . Pr??diction dehors de la plage des donn??es utilis??es pour construire le mod??le est connu comme extrapolation et il est plus risqu??.

R??gression non lin??aire

Lorsque la fonction de mod??le ne est pas lin??aire dans les param??tres de la somme des carr??s doit ??tre minimis??e par une proc??dure it??rative. Cela introduit de nombreuses complications qui sont r??sum??es dans les diff??rences entre lin??aire et non lin??aire des moindres carr??s

D'autres m??thodes

Bien que les param??tres d'un mod??le de r??gression sont habituellement estim??s en utilisant la m??thode des moindres carr??s, d'autres proc??d??s qui ont ??t?? utilis??s sont les suivants:

M??thodes bay??siennes
Minimisation des ??carts absolus, conduisant ?? r??gression quantile
R??gression non param??trique. Cette approche n??cessite un grand nombre d'observations, que les donn??es sont utilis??es pour construire la structure du mod??le ainsi que d'estimer les param??tres du mod??le. Ils sont g??n??ralement de calcul intensif.

Logiciel

Tous les grands progiciels statistiques effectuent les types courants de l'analyse de r??gression correctement et d'une mani??re conviviale. La r??gression lin??aire simple peut ??tre fait en quelques tableurs. Il ya un certain nombre de programmes de logiciels qui effectuent des formes sp??cialis??es de la r??gression, et les experts peuvent choisir d'??crire leur propre code pour l'aide langages de programmation ou de statistiques un logiciel d'analyse num??rique.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Regression_analysis&oldid=198424867 "