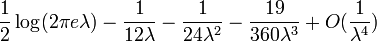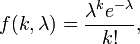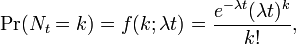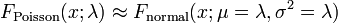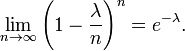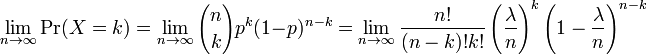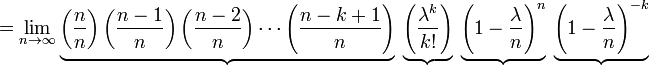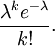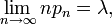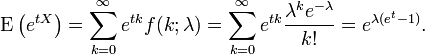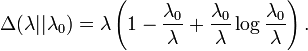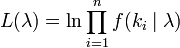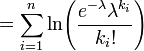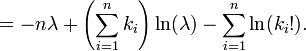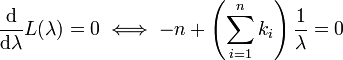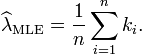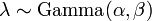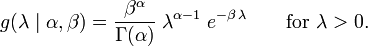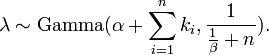Distribución de Poisson
Acerca de este escuelas selección Wikipedia
SOS Children, una organización benéfica educación , organizó esta selección. Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de niños.
Función de probabilidad 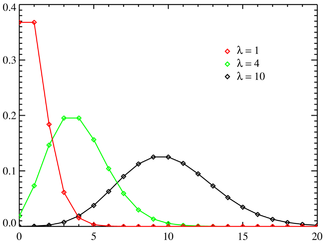 El eje horizontal es el índice k. La función se define únicamente en valores enteros de k. Las líneas de conexión son sólo guías para el ojo y no indican la continuidad. | |
Función de distribución acumulativa  El eje horizontal es el índice k. | |
| Parámetros | 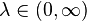 |
|---|---|
| Apoyo | 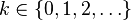 |
| PMF | 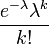 |
| CDF | 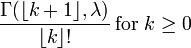 (Donde |
| Significar | 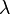 |
| Mediana | 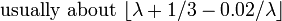 |
| Modo | 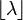 y y 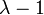 si si 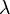 es un número entero es un número entero |
| Desacuerdo | 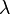 |
| Oblicuidad | 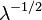 |
| Ex. curtosis | 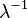 |
| Entropía | ![\ Lambda [1 \ -! \ \ Ln (\ lambda)]! \ + \ E ^ {- \ lambda} \ sum_ {k = 0} ^ \ infty \ frac {\ lambda ^ k \ ln (k! )} {k!}](../../images/97/9713.png) (Para la gran |
| MGF | 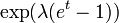 |
| CF | 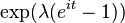 |
En teoría de la probabilidad y estadística , la distribución de Poisson es una distribución de probabilidad discreta que expresa la probabilidad de que una serie de eventos que ocurren en un período fijo de tiempo si se producen estos eventos con una tasa media conocida y con independencia del tiempo transcurrido desde el último evento. La distribución de Poisson también puede ser utilizado para el número de eventos en otros intervalos especificados como la distancia, área o volumen.
La distribución fue descubierto por Siméon-Denis Poisson ( 1781 - 1840 ) y se publicará, con su teoría de la probabilidad, en 1838 en su obra Recherches sur la probabilité des jugements en matières criminelles et matière civile ("La investigación sobre la probabilidad de resoluciones judiciales en materia penal y civil") . El trabajo se centró en determinadas variables aleatorias N que cuenta, entre otras cosas, una serie de sucesos discretos (a veces llamado "llegadas") que tienen lugar durante un tiempo -interval de longitud dada. Si el número esperado de ocurrencias en este intervalo es λ, entonces la probabilidad de que hay k exactamente ocurrencias (siendo k un no negativo entero , k = 0, 1, 2, ...) es igual a
donde
- e es la base del logaritmo natural (e = 2,71828 ...)
- k es el número de ocurrencias de un evento - la probabilidad de que se da por la función de
- k! es el factorial de k
- λ es un positivo número real , igual al número esperado de sucesos que ocurren durante el intervalo dado. Por ejemplo, si se producen los eventos en promedio cada 4 minutos, y usted está interesado en el número de eventos que ocurren en un intervalo de 10 minutos, se utiliza como modelo una distribución de Poisson con λ = 10/4 = 2,5.
Como una función de k, este es el función de masa de probabilidad. La distribución de Poisson se puede derivar como un caso límite de la distribución binomial .
La distribución de Poisson se puede aplicar a sistemas con un gran número de posibles eventos, cada uno de los cuales es poco frecuente. Un ejemplo clásico es la desintegración nuclear de los átomos.
La distribución de Poisson a veces se llama una Poissonian, análoga a la de Gauss plazo para un Gauss o distribución normal .
Ruido de Poisson y caracterizar pequeñas apariciones
El parámetro λ no es sólo la media número de ocurrencias 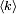 , Sino también su varianza
, Sino también su varianza  (Véase el cuadro). Por lo tanto, el número de apariciones observadas fluctúa alrededor de su media λ con una desviación estándar
(Véase el cuadro). Por lo tanto, el número de apariciones observadas fluctúa alrededor de su media λ con una desviación estándar 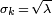 . Estas fluctuaciones se denotan como ruido de Poisson o (particularmente en la electrónica) como ruido de disparo.
. Estas fluctuaciones se denotan como ruido de Poisson o (particularmente en la electrónica) como ruido de disparo.
La correlación de la media y la desviación estándar en el conteo, los sucesos discretos independientes es útil científicamente. Al monitorear cómo las fluctuaciones varían con la señal media, se puede estimar la contribución de una sola aparición, incluso si esa contribución es demasiado pequeño para ser detectado directamente. Por ejemplo, el e carga de un electrón puede ser estimado mediante la correlación de la magnitud de una corriente eléctrica con su ruido de disparo. Si N electrones pasan a un punto en un tiempo dado t en promedio, la media corriente es I = es / t; ya que las fluctuaciones de corriente deben ser del orden 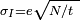 (Es decir, la varianza del proceso de Poisson), la carga e puede estimarse a partir de la relación
(Es decir, la varianza del proceso de Poisson), la carga e puede estimarse a partir de la relación 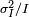 . Un ejemplo cotidiano es el grano que aparece como fotografías son ampliada; el grano se debe a las fluctuaciones de Poisson en el número de reducción de plata granos, no a los propios granos individuales. Al correlacionar el grado de aspereza con el grado de ampliación, se puede estimar la contribución de un grano individual (que es de lo contrario demasiado pequeños para ser vistos sin ayuda). Muchas otras aplicaciones moleculares de ruido de Poisson se han desarrollado, por ejemplo, la estimación de la densidad de número de moléculas de receptores en una membrana celular.
. Un ejemplo cotidiano es el grano que aparece como fotografías son ampliada; el grano se debe a las fluctuaciones de Poisson en el número de reducción de plata granos, no a los propios granos individuales. Al correlacionar el grado de aspereza con el grado de ampliación, se puede estimar la contribución de un grano individual (que es de lo contrario demasiado pequeños para ser vistos sin ayuda). Muchas otras aplicaciones moleculares de ruido de Poisson se han desarrollado, por ejemplo, la estimación de la densidad de número de moléculas de receptores en una membrana celular.
Distribuciones Relacionados
- Si
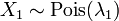 y
y 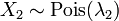 entonces la diferencia
entonces la diferencia 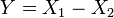 sigue una Distribución Skellam.
sigue una Distribución Skellam. - Si
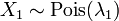 y
y 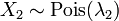 son independientes, y
son independientes, y 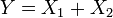 , Entonces la distribución de
, Entonces la distribución de 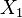 en condicional
en condicional 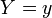 es una binomial . Específicamente,
es una binomial . Específicamente, 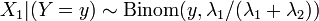 . Más generalmente, si X 1, X 2, ..., X n son variables aleatorias de Poisson con parámetros λ 1, λ 2, ..., n λ entonces
. Más generalmente, si X 1, X 2, ..., X n son variables aleatorias de Poisson con parámetros λ 1, λ 2, ..., n λ entonces 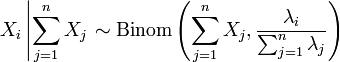
- La distribución de Poisson se puede derivar como un caso límite de la distribución binomial como el número de ensayos tiende a infinito y la número esperado de éxitos permanece fijo. Por lo tanto, se puede utilizar como una aproximación de la distribución binomial si n es suficientemente grande y p es suficientemente pequeño. Hay una regla que indica que la distribución de Poisson es una buena aproximación de la distribución binomial si n es al menos 20 y p es menor que o igual a 0,05. De acuerdo con esta regla a la aproximación es excelente si n ≥ 100 y np ≤ 10.
- Para valores suficientemente grandes de λ, (digamos λ> 1000), la distribución normal con media λ y λ varianza, es una excelente aproximación a la distribución de Poisson. Si λ es mayor que aproximadamente 10, entonces la distribución normal es una buena aproximación si un apropiado corrección de continuidad se lleva a cabo, es decir, P (X ≤ x), donde (minúsculas) x es un entero no negativo, se sustituye por P (X ≤ x + 0.5).
- Si el número de llegadas en un tiempo dado sigue la distribución de Poisson, con media =
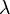 , A continuación, las longitudes de los tiempos entre llegadas siguen la distribución exponencial , con una tasa
, A continuación, las longitudes de los tiempos entre llegadas siguen la distribución exponencial , con una tasa 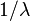 .
.
Aparición
La distribución de Poisson surge en relación con Procesos de Poisson. Se aplica a diversos fenómenos de naturaleza discreta (es decir, aquellos que puede suceder 0, 1, 2, 3, ... veces durante un período de tiempo determinado o en un área dada) siempre que la probabilidad de que el fenómeno ocurre es constante en tiempo o espacio. Ejemplos de eventos que pueden ser modelados como una distribución de Poisson incluyen:
- El número de coches que pasan a través de un cierto punto en un camino (a una distancia suficiente de las luces de tráfico) durante un período determinado de tiempo.
- El número de faltas de ortografía uno hace mientras se escribe una sola página.
- El número de llamadas telefónicas a una centro de llamadas por minuto.
- El número de veces que un servidor web se accede por minuto.
- El número de Roadkill (animales muertos) encontrado por unidad de longitud de la carretera.
- El número de mutaciones en un tramo dado de ADN después de una cierta cantidad de radiación.
- El número de inestables núcleos que decayó dentro de un período de tiempo determinado en una pieza de sustancia radiactiva. La radiactividad de la sustancia se debilitará con el tiempo, por lo que el intervalo de tiempo total utilizado en el modelo debe ser significativamente menor que la significa tiempo de vida de la sustancia.
- El número de árboles de pino por unidad de área de bosque mixto.
- El número de estrellas en un volumen dado de espacio.
- El número de soldados muertos por caballos patadas cada año en cada uno de los cuerpos en el Caballería prusiana. Este ejemplo fue hecho famoso por un libro de Ladislao Josephovich Bortkiewicz ( 1868 - 1931 ).
- La distribución de los receptores de las células visuales en la retina de la humano ojo .
- El número de bombillas que se queman en una cierta cantidad de tiempo.
- El número de virus que pueden infectar una célula en cultivo celular.
- El número de células madre hematopoyéticas en una muestra de células de médula ósea no fraccionada.
- El número de invenciones de un inventor sobre su carrera.
- El número de partículas que "dispersión" off de un objetivo en un experimento de física nuclear de energía o alta.
[Nota: los intervalos entre eventos sucesivos de Poisson se relacionan-recíprocamente, a raíz de la distribución exponencial . Por ejemplo, la vida útil de una bombilla, o el tiempo de espera entre autobuses.]
¿Cómo surge esta distribución? - La ley de eventos raros
En varios de los ejemplos ejemplo-para arriba, el número que se está contado de mutaciones en una determinada secuencia de ADN los eventos son en realidad los resultados de ensayos discretos, y sería más precisamente ser modelado utilizando la distribución binomial . Sin embargo, la distribución binomial con parámetros n y λ / n, es decir, la distribución de probabilidad de que el número de éxitos en n ensayos, con λ probabilidad / n de éxito en cada intento, se aproxima a la distribución de Poisson con valor esperado λ como n tiende a infinito . Este límite es a veces conocida como la ley de eventos raros, aunque este nombre puede ser engañoso porque los eventos en un proceso de Poisson no necesitan ser rara (el número de llamadas telefónicas a una centralita ocupado en una hora sigue una distribución de Poisson, pero estos eventos no se consideraría raro). Se proporciona un medio por el cual para aproximar variables aleatorias usando la distribución de Poisson en lugar de la distribución binomial más engorroso.
Aquí están los detalles. En primer lugar, recordar de cálculo que
Sea p = λ / n. Entonces tenemos
Como n se acerca ∞, la expresión sobre la primera underbrace se aproxima a 1; el segundo se mantiene constante ya que "n" no aparece en ella en absoluto; la tercera se acerca e -λ; y la cuarta expresión se aproxima a 1.
En consecuencia, el límite es
Más en general, cada vez que una secuencia de variables aleatorias binomial con parámetros n y p es tal que n
la secuencia converge en la distribución de una variable aleatoria de Poisson con λ media (véase, por ejemplo, ley de eventos raros).
Propiedades
- La valor esperado de una variable aleatoria de distribución de Poisson es igual a λ y también lo es su varianza . Cuanto más alto momentos de la distribución de Poisson son Polinomios de Touchard en λ, cuyos coeficientes tienen una combinatoria significado. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces La fórmula de Dobinski dice que el n-ésimo momento es igual al número de particiones de un conjunto de tamaño n.
- El modo de una variable aleatoria de Poisson-distribuido con λ no entero es igual a
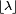 , Que es el mayor entero menor o igual a λ. Esto también se escribe como piso (λ). Cuando λ es un número entero positivo, los modos son λ y λ - 1.
, Que es el mayor entero menor o igual a λ. Esto también se escribe como piso (λ). Cuando λ es un número entero positivo, los modos son λ y λ - 1.
- Sumas de variables aleatorias distribuidas-Poisson:
- Si
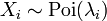 sigue una distribución de Poisson con parámetro
sigue una distribución de Poisson con parámetro 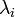 y
y 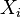 son independiente, entonces
son independiente, entonces 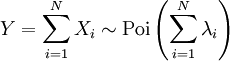 También sigue una distribución de Poisson cuyo parámetro es la suma de los parámetros de los componentes.
También sigue una distribución de Poisson cuyo parámetro es la suma de los parámetros de los componentes.
- La función generadora de momentos de la distribución de Poisson con λ valor esperado es
- Toda la cumulantes de la distribución de Poisson son iguales a la λ valor esperado. El enésimo momento factorial de la distribución de Poisson es λ n.
- Las distribuciones de Poisson se infinitamente divisible distribuciones de probabilidad.
- El dirigida Kullback-Leibler divergencia entre Poi (λ 0) y Poi (λ) está dada por
Generación de distribución de Poisson-variables aleatorias
Una forma sencilla de generar números de Poisson-distribuido al azar está dada por Knuth , ver Referencias a continuación.
algoritmo poisson número aleatorio (Knuth):
en eso:
Sea L ← e -λ, k ← 0 yp ← 1.
hacer:
k ← k + 1.
Generar números aleatorios uniformes u en [0,1] y dejar p ← p × u.
mientras que p ≥ L.
volver k - 1.
Aunque simple, la complejidad es lineal en λ. Hay muchos otros algoritmos para superar esto. Algunos se dan en Ahrens & Dieter, ver Referencias a continuación.
La estimación de parámetros
Máxima verosimilitud
Dada una muestra de n valores medidos k i deseamos para estimar el valor del parámetro λ de la población de Poisson de la que se extrajo la muestra. Para calcular la valor de máxima verosimilitud, se forma la función de log-verosimilitud
Tome la derivada de L con respecto a λ y equipararlo a cero:
Despejando λ se obtiene la estimación de máxima verosimilitud de λ:
Dado que cada observación tiene expectativa por lo que λ Qué significa esto muestra. Por lo tanto, es una estimador insesgado de λ. También es un estimador eficiente, es decir, su varianza de estimación alcanza el Cramer-Rao límite inferior (CRLB).
Inferencia bayesiana
En la inferencia bayesiana , la conjugado previa para el parámetro de tasa λ de la distribución de Poisson es la Distribución Gamma. Dejar
denotar que λ se distribuye de acuerdo con el Gamma densidad g parametrizado en términos de una forma parámetro α y una inversa β parámetro de escala:
Entonces, dada la misma muestra de n midieron los valores de k i como antes, y un previo de Gamma (α, β), la distribución posterior es
La media posterior E [λ] se aproxima a la estimación de máxima verosimilitud 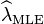 en el límite cuando
en el límite cuando 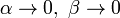 .
.
La distribución posterior de predicción de datos adicional es un Gamma-Poisson (es decir, ) distribución binomial negativa.
La "ley de los números pequeños"
La ley de la palabra se utiliza a veces como sinónimo de distribución de probabilidad , y la convergencia en ley significa la convergencia en la distribución. En consecuencia, la distribución de Poisson a veces se llama la ley de los números pequeños, ya que es la distribución de probabilidad de que el número de ocurrencias de un evento que ocurre raramente, pero tiene muchas posibilidades de suceder. La ley de los pequeños números es un libro de Ladislao Bortkiewicz acerca de la distribución de Poisson, publicado en 1898 . Algunos historiadores de las matemáticas han argumentado que la distribución de Poisson debería haber sido llamado la distribución Bortkiewicz.
Calcular una aproximación de la probabilidad de Poisson
Cuando k se hace grande (> 20) se necesita el uso de registros y aproximaciones factoriales. He aquí un ejemplo escrito en Java.
/ ** Calcula una aproximación de la probabilidad de Poisson. *param Media - lambda, el número medio de ocurrencias *param observado - el número real de las ocurrencias observadas *return ln (probabilidad de Poisson) - el logaritmo natural de la probabilidad de Poisson. */ public static double poissonProbabilityApproximation ( double mean, int observed ) { double k = observed ; double a = k * Math . log ( mean ) ; double b = - mean ; return a + b - factorialApproximation ( k ) ; } /**Srinivasa Ramanujan ln (n!) Estimación factorial. * Bueno para valores grandes de n. *return Ln (n!) */ public static double factorialApproximation ( double n ) { if ( n < 2 . ) return 0 ; double a = n * Math . log ( n ) - n ; double b = Math . log ( n * ( 1 . + 4 . * n * ( 1 . + 2 . * n ) ) ) / 6 . ; return a + b + Math . log ( Math . PI ) / 2 . ; }
Herramientas de visualización en línea
- SOCR GUI distribución
- De TAMU Interactivo Distribución de Poisson
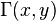 es el Función gamma incompleta)
es el Función gamma incompleta)