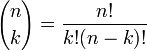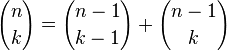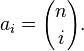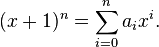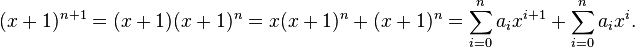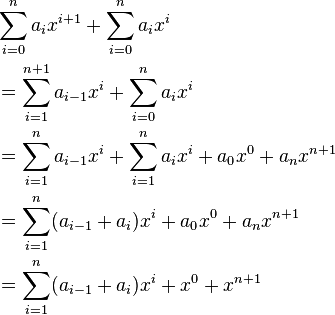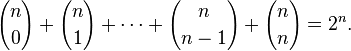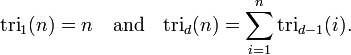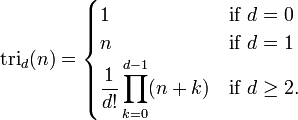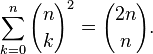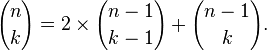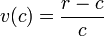El triángulo de Pascal

Temas relacionados: Matemáticas

Sabías ...

SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/

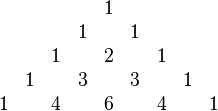
$\ Begin {matriz} &&&&& 1 \\ &&&& 1 && 1 \\ &&& 1 && 2 && 1 \\ 1 && && && 3 3 && 1 \\ & 1 && && 4 6 4 && && 1 \ end {matriz}$

Las primeras cinco filas del triángulo de Pascal

En matemáticas , el triángulo de Pascal es una disposición geométrica de los coeficientes de dos términos en un triángulo . Lleva el nombre de Blaise Pascal en gran parte del mundo occidental, aunque otros matemáticos estudiaron siglos antes que él en la India , Persia , China, y Italia . Las filas del triángulo de Pascal se enumeran convencionalmente empezando con la fila cero, y los números de las filas impares son generalmente escalonados con respecto a los números en filas pares. Una construcción simple del triángulo procede de la siguiente manera. En la fila cero, escribir solamente el número 1. Luego, para la construcción de los elementos de las filas siguientes, agregue el número directamente encima ya la izquierda con el número justo encima ya la derecha para encontrar el nuevo valor. Si bien el número a la derecha oa la izquierda no está presente, sustituir un cero en su lugar. Por ejemplo, el primer número de la primera fila es 0 + 1 = 1, mientras que los números 1 y 3 de la tercera fila se agregan para producir el número 4 en la cuarta fila.

Cada número en el triángulo es la suma de los dos directamente por encima de ella.

Esta construcción está relacionado con los coeficientes binomiales por Regla de Pascal, que establece que si

${N \ choose k} = \ frac {n!} {K! (N-k)!}$

es el k coeficiente binomial en el expansión binomial de (x + y) ^n, donde n! es el factorial de n, entonces

${N \ choose k} = {n-1 \ choose k-1} + {n-1 \ choose k}$

para cualquier número entero no negativo n y k cualquier número entero entre 0 y n.

El triángulo de Pascal tiene mayor generalizaciones dimensionales. La versión en tres dimensiones se llama Pirámide de Pascal o tetraedro de Pascal, mientras que las versiones generales se llaman Simplices de Pascal - ver tambien pirámide , tetraedro , y simplex.

El triángulo

A continuación se presentan filas de cero a dieciséis del triángulo de Pascal:

                                                 1
                                              1 1
                                           1 2 1
                                        1 3 3 1
                                     1 4 6 4 1
                                  1 5 10 10 5 1
                               1 6 15 20 15 6 1
                            1 7 21 35 35 21 7 1
                         1 8 28 56 70 56 28 8 1
                      1 9 36 84 126 126 84 36 9 1
                   1 10 45 120 210 252 210 120 45 10 1
                1 11 55 165 330 462 462 330 165 55 11 1
             1 12 66 220 495 792 924 792 495 220 66 12 1
          1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
       1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
    1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

Triángulo y binomiales expansiones de Pascal

El triángulo de Pascal determina los coeficientes que se plantean en expansiones binomial. Por ejemplo, considere la expansión

(X + y) = ² x ² + 2 xy + y ² = 1 x ² y ⁰ + 2 x ¹ y ¹ + 1 x ⁰ y ^2.

Aviso La coeficientes son los números en la fila dos del triángulo de Pascal: 1, 2, 1. En general, cuando un binomial como x + y se eleva a una potencia entera positiva tenemos:

(X + y) ⁿ = a ₀ x ⁿ + a ₁ x ^{n -1} y + ₂ x ^{N -2} y ² + ... + a _{n -1} xy ^{n -1} + a _n y ^n,

donde los coeficientes a _i en esta expansión son, precisamente, los números en la fila n del triángulo de Pascal. En otras palabras,

$a_i = {n \ choose i}.$

Este es el teorema del binomio.

Nótese que toda diagonal derecha del triángulo de Pascal corresponde al coeficiente de y ⁿ en estas expansiones binomiales, mientras que los próximos diagonal corresponde al coeficiente de xy ^{n -1} y así sucesivamente.

Para ver cómo el teorema del binomio se refiere a la simple construcción del triángulo de Pascal, considere el problema de calcular los coeficientes del desarrollo de (x + 1) ^{n + 1} en términos de los coeficientes correspondientes de (x + 1) ⁿ (ajuste y = 1 para simplificar). Supongamos entonces que

$(X + 1) ^ n = \ sum_ {i = 0} ^ n a_i x ^ i.$

Ahora

$(X + 1) ^ {n + 1} = (x + 1) (x + 1) ^ n = x (x + 1) ^ n + (x + 1) ^ n = \ sum_ {i = 0} ^ n a_i x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i.$

Las dos sumas se pueden reorganizar la siguiente manera:

$\ Begin {align} & \ sum_ {i = 0} ^ {n} a_ {i} x ^ {i + 1} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n + 1} a_ {i-1} x ^ {i} + \ sum_ {i = 0} ^ n a_i x ^ i \\ & {} = \ sum_ {i = 1} ^ {n} a_ {i-1} x ^ {i} + \ sum_ {i = 1} ^ n a_i x ^ i + a_0x ^ 0 + a_ {n} x ^ {n + 1} \\ & {} = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {i} + a_0x ^ 0 + a_ {n} x ^ {n + 1} \\ & {} = \ sum_ {i = 1} ^ {n} (a_ {i-1} + a_i) x ^ {i} + x ^ 0 + x ^ {n + 1} \ end {align}$

(Debido a cómo criar a un polinomio a una planta de energía, un ₀ = a _n = 1).

Ahora tenemos una expresión para el polinomio (x + 1) ^{n + 1} en términos de los coeficientes de (x + 1) ⁿ (estos son los a _i s), que es lo que necesitamos si queremos expresar una línea en términos de la línea por encima de ella. Recordemos que todos los términos en una diagonal que va desde la parte superior izquierda a la inferior derecha se corresponden con la misma potencia de x, y que los términos-A son los coeficientes del polinomio (x + 1) ^n, y que son determinantes los coeficientes de (x + 1) ^{n 1.} Ahora, para cualquier i dada no 0 o n + 1, el coeficiente del término x ⁱ en el polinomio (x + 1) ^{n 1} es igual a a _i (la figura de arriba y a la izquierda de la figura que se determine , ya que está en la misma diagonal) + un _{i -1} (la figura a la derecha inmediata de la primera figura). Este es de hecho la regla simple para construir triángulo fila por fila de Pascal.

No es difícil convertir este argumento en una prueba (por inducción matemática) del teorema del binomio.

Una consecuencia interesante del teorema binomial se obtiene mediante el establecimiento de dos variables xey igual a uno. En este caso, sabemos que 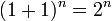$(1 + 1) ^ n = 2 ^ n$ , Y entonces

${N \ choose 0} + {n \ choose 1} + \ cdots + {n \ choose n-1} + {n \ choose n} = 2 ^ n.$

En otras palabras, la suma de las entradas de la n-ésima fila del triángulo de Pascal es la n-ésima potencia de 2.

Patrones y propiedades

El triángulo de Pascal tiene muchas propiedades y contiene muchos patrones de números.

Las diagonales

Algunos patrones simples son inmediatamente evidentes en las diagonales del triángulo de Pascal:

Las diagonales van a lo largo de los bordes izquierdo y derecho contienen sólo 1 de.
Las diagonales al lado de las diagonales borde contienen los números naturales en orden.
Mover hacia el interior, el siguiente par de diagonales contiene la números triangulares en orden.
El siguiente par de diagonales contiene la números tetraédricos en orden, y la próxima dar par números pentatope. En general, cada siguiente par de diagonales contiene la siguiente "d dimensional superior - simplex "números, que pueden definirse como

$\ Textrm {tri} _1 (n) = n \ quad \ mbox {y} \ quad \ textrm {tri} _ {d} (n) = \ sum_ {i = 1} ^ n \ mathrm {tri} _ {d -1} (i).$

Una fórmula alternativa es la siguiente:

$\ Textrm {tri} _D (n) = \ begin {casos} 1 & \ mbox {si} d = 0 \\ n & \ mbox {si} d = 1 \\ \ displaystyle \ frac {1} {d!} \ prod_ {k = 0} ^ {d-1} (n + k) & \ mbox {si} d \ ge 2. \ end {casos}$

El significado geométrico de una función tri _d es: tri _d (1) = 1 para todos d. Construir un d - dimensional triángulo (un triángulo 3-dimensional es un tetraedro ) mediante la colocación de puntos adicionales por debajo de un punto inicial, correspondiente a tri _d (1) = 1. Colocar estos puntos en una manera análoga a la colocación de los números en el triángulo de Pascal. Para encontrar tri _d (x), con un total de x puntos que componen la forma deseada. tri _d (x), entonces es igual al número total de puntos de la forma. Un triángulo 1-dimensional es simplemente una línea, y por lo tanto tri ₁ (x) = x, que es la secuencia de los números naturales. El número de puntos en cada capa corresponde a tri _{d - 1} (x).

Triángulo de Sierpinski

Otros patrones y propiedades

El patrón obtenido por la coloración sólo los números impares en el triángulo de Pascal se asemeja mucho al fractal llamado Triángulo de Sierpinski, y esta semejanza se vuelve más y más precisa a medida que más filas se consideran; en el límite, como el número de filas se aproxima al infinito, el patrón resultante es el triángulo de Sierpinski. De manera más general, los números podrían ser de color diferente en función de si son o no son múltiplos de 3, 4, etc .; esto da lugar a otros patrones y combinaciones.

Imagínese cada número en el triángulo es un nodo en una red que está conectado a los números adyacentes por encima y por debajo de ella. Ahora, para cualquier nodo de la red, contar el número de caminos hay en la red (sin dar marcha atrás) que conectan este nodo para el nodo superior (1) del triángulo. La respuesta es el número Pascal asociado a ese nodo. La interpretación del número en el triángulo de Pascal como el número de rutas de acceso a ese número desde la punta significa que en una Con forma de triángulo Plinko tablero de juego, la probabilidad de premios más cerca del centro de ganar será más alto que en los bordes premios ganadora.

El valor de cada fila, si cada número en que se considera como un lugar decimal y números mayores que 9 se realizan sobre en consecuencia, es una potencia de 11 (en concreto, 11 ^n, donde n es el número de la fila). Por ejemplo, la fila dos lee '1, 2, 1', que es 11 ² (121). En la fila cinco, '1, 5, 10, 10, 5, 1' se traduce a 161.051 después de llevar los valores a lo largo, que es de 11 ^5. Esta propiedad se explica fácilmente haciendo x = 10 en la expansión binomial de (x + 1) ^{número de la fila,} y el ajuste de los valores de encajar en el sistema de numeración decimal.

Patrones más sutiles

Hay también, patrones sutiles más sorprendentes. De un solo elemento del triángulo, una línea diagonal más superficial se puede formar moviendo continuamente un elemento a la derecha, a continuación, un elemento a la parte inferior derecha, o por ir en la dirección opuesta. Un ejemplo es la línea con los elementos 1, 6, 5, 1, que comienza desde la fila 1, 3, 3, 1 y termina tres filas hacia abajo. Tal "diagonal" tiene una suma que es un número de Fibonacci . En el caso del ejemplo, el número de Fibonacci es 13:

                                        1
                                     1 1
                                  1 2 1
                               1 → 3 ↓ 3 1
                            1 4 → 6 → 4 ↓ 1
                         1 5 10 10 → 5 → 1 ↓
                      1 → 6 ↓ 15 20 15 6 1 →
                    1 7 → 21 35 35 21 7 1
                 1 8 28 56 70 56 28 8 1
               1 9 36 84 126 126 84 36 9 1
             1 10 45 120 210 252 210 120 45 10 1
           1 11 55 165 330 462 462 330 165 55 11 1
         1 12 66 220 495 792 924 792 495 220 66 12 1
       1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
     1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 
   1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1

El segundo puesto de relieve diagonal tiene una suma de 233. Los números 'saltado sobre' entre el derecho movimiento y el movimiento hacia abajo-derecha también suma a los números de Fibonacci, siendo los números 'entre' las cantidades formadas por la primera construcción. Por ejemplo, los números saltan en el primero resaltados diagonal son 3, 4 y 1, por lo que 8.

Además, si se toma la fila m para indicar fila 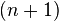$(N + 1)$ , La suma de los cuadrados de los elementos de la fila m es igual al elemento medio de la fila 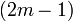$(2m-1)$ . Por ejemplo, 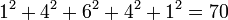$1 ^ 2 + 4 ^ 2 + 6 + 4 ^ 2 ^ 2 + 1 = 2 ^ 70$ . En forma general:

$\ Sum_ {k = 0} ^ n {n \ choose k} ^ 2 = {2n \ elegir n}.$

Otro patrón interesante es que en cualquier fila m, donde m es impar, el término medio, menos el término de dos puntos a la izquierda es igual a una Número catalán, concretamente el (m + 1) / 2 número catalán. Por ejemplo: en la fila 5, 6 - 1 = 5, que es el número catalán ^3º, y (5 + 1) / 2 = 3.

Además, la suma de los elementos de la fila m es igual a 2 ^{m -1.} Por ejemplo, la suma de los elementos de la fila 5 es 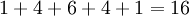$1 + 4 + 6 + 4 + 1 = 16$ , Que es igual a 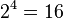$2 ^ 4 = 16$ . Esto se deduce del teorema del binomio demostró anteriormente, aplicado a (1 + 1) ^{m -1.}

Algunos de los números en el triángulo de Pascal se correlacionan con los números en Triángulo de Lozanić.

Otra propiedad interesante del triángulo de Pascal es que en las filas donde el segundo número (el primero número siguiente 1) es de primera, todos los términos de esa fila, excepto los 1s son múltiplos de que prime.

Matriz binomial exponencial matriz (ilustración para 5 × 5 matrices). Todos los puntos representan 0.

La matriz exponencial

Debido a su construcción simple por factoriales, una representación muy básico del triángulo de Pascal en términos de la matriz exponencial se puede dar: el triángulo de Pascal es la exponencial de la matriz que tiene la secuencia 1, 2, 3, 4, ... en su subdiagonal y cero en todas partes.

Propiedades geométricas

Triángulo de Pascal se puede utilizar como un tabla de consulta para el número de elementos dimensionados de manera arbitraria dentro de una sola versión dimensionado arbitrariamente de un triángulo (conocido como simplex). Por ejemplo, considere la tercera línea del triángulo, con los valores 1, 3, 3, 1. triángulo A 2-dimensional tiene un elemento de 2 dimensiones (en sí misma), tres elementos 1-dimensionales (líneas o bordes), y tres elementos 0-dimensionales ( vértices o esquinas). El significado del número final (1) es más difícil de explicar (pero véase más abajo). Continuando con nuestro ejemplo, un tetraedro tiene un elemento 3-dimensional (en sí misma), cuatro elementos 2-dimensionales (caras), seis elementos 1-dimensionales (bordes), y cuatro elementos 0-dimensionales (vértices). Adición de la final 1 de nuevo, estos valores corresponden a la cuarta fila del triángulo (1, 4, 6, 4, 1). Línea 1 corresponde a un punto, y la línea 2 corresponde a un segmento de línea (diada). Este patrón continúa arbitrariamente altos dimensionado hiper-tetraedros (simplices).

Para entender por qué existe este patrón, primero hay que entender que el proceso de construcción de un n -simplex de un (n - 1) -simplex consiste simplemente en añadir un nuevo vértice a este último, colocado de tal manera que este nuevo vértice se encuentra fuera de la espacio de la simplex original, y conectándolo a todos los vértices originales. Como ejemplo, considere el caso de la construcción de un tetraedro de un triángulo, el último de cuyos elementos se enumeran por la fila 3 del triángulo de Pascal: 1 cara, 3 aristas y 3 vértices (el significado de la final 1 se explicará en breve) . Para construir un tetraedro a partir de un triángulo, colocamos un nuevo vértice por encima del plano del triángulo y conectamos este vértice a los tres vértices del triángulo original.

El número de un elemento dimensional dada en el tetraedro es ahora la suma de dos números: primero el número de ese elemento que se encuentra en el triángulo original, más el número de nuevos elementos, cada uno de los cuales se construye sobre elementos de una dimensión menor de la triángulo original. Así, en el tetraedro, el número de células (elementos poliédricos) es 0 (el triángulo original posee ninguno) + 1 (construida sobre la faz única del triángulo original) = 1; el número de caras es 1 (el propio triángulo original) + 3 (las nuevas caras, cada una construida sobre un borde de la triángulo original) = 4; el número de aristas es 3 (desde el triángulo original) + 3 (las nuevas bordes, cada una construida sobre un vértice del triángulo original) = 6; el número de nuevos vértices es 3 (desde el triángulo original) + 1 (el nuevo vértice que se añadió para crear el tetraedro del triángulo) = 4. Este proceso de sumando el número de elementos de una dimensión dada a los de una dimensión menos para llegar a la cantidad de la antigua encontrado en la siguiente simplex superior es equivalente al proceso de suma de dos números adyacentes en una fila del triángulo de Pascal para producir el número de abajo. Así, el significado del número final (1) en una fila del triángulo de Pascal, sea entendido como que representa el nuevo vértice que se va a añadir a la simplex representado por esa fila para dar el siguiente simplex superior representado por la siguiente fila. Este nuevo vértice se une a cada elemento en el simplex original, para producir un nuevo elemento de una dimensión mayor en la nueva simplex, y este es el origen del patrón encontrado para ser idéntica a la observada en el triángulo de Pascal.

Un patrón similar se observa relativas a las plazas , a diferencia de los triángulos. Para encontrar el patrón, se debe construir un análogo al triángulo de Pascal, cuyas entradas son los coeficientes de (x + 2) ^{Número de fila,} en lugar de (x + 1) ^{número de fila.} Hay un par de maneras de hacer esto. El más simple es comenzar con la fila 0 = 1 y la fila 1 = 1, 2. Proceder para construir los triángulos analógicas de acuerdo con la siguiente regla:

${N \ choose k} = 2 \ épocas {n-1 \ eligen k-1} + {n-1 \ eligen k}.$

Es decir, elegir un par de números de acuerdo a las reglas del triángulo de Pascal, pero el doble del de la izquierda antes de añadir. Esto se traduce en:

                              1
                          1 2
                      1 4 4
                  1 6 12 8
              1 8 24 32 16
          1 10 40 80 80 32
      1 12 60 160 240 192 64
  1 14 84 280 560 672 448 128

La otra forma de fabricación de este triángulo es comenzar con el triángulo de Pascal y multiplicar cada entrada por 2 ^k, donde k es la posición en la fila del número dado. Por ejemplo, el segundo valor en la fila 4 del triángulo de Pascal es 6 (la pendiente de 1s corresponde a la entrada de orden cero en cada fila). Para obtener el valor que reside en la posición correspondiente en el triángulo analógica, multiplicar 6 por 2 ^{Posición Number} = 6 × 2 ² = 6 × 4 = 24. Ahora que el triángulo analógica se ha construido, el número de elementos de cualquier dimensión que componer un dimensionado arbitrariamente cubo (llamado hipercubo) se puede leer en la mesa de una manera análoga a la del triángulo de Pascal. Por ejemplo, el número de elementos 2-dimensionales en un cubo 2-dimensional (un cuadrado) es uno, el número de elementos 1-dimensionales (lados, o líneas) es 4, y el número de elementos 0-dimensionales (puntos, o vértices) es 4. Esto coincide con la segunda fila de la tabla (1, 4, 4). Un cubo tiene 1 cubo, 6 caras, bordes, 12 y 8 vértices, que corresponde a la siguiente línea del triángulo analógica (1, 6, 12, 8). Este patrón continúa indefinidamente.

Para entender por qué existe este patrón, primero reconocer que la construcción de un n -cube de un (n - 1) -cube se hace simplemente duplicando la figura original y desplazándola a cierta distancia (para un n -cube regular, la longitud del borde ) ortogonal al espacio de la figura original, entonces la conexión de cada vértice de la nueva figura a su correspondiente vértice de la original. Este proceso de duplicación inicial es la razón por la cual, para enumerar los elementos tridimensionales de una n -cube, hay que duplicar la primera de un par de números en una fila de este análogo del triángulo de Pascal antes de sumar para dar el número a continuación. Así pues, la duplicación inicial produce el número de elementos "originales" que se encuentra en la siguiente más alta n -cube y, como antes, los nuevos elementos se basan en las de una dimensión menor (bordes sobre vértices, caras en los bordes, etc.). Una vez más, el último número de una fila representa el número de nuevos vértices que se añaden para generar la siguiente más alta n -cube.

En este triángulo, la suma de los elementos de la fila m es igual a 3 ^{m - 1} Una vez más, utilizar los elementos de la fila 5 como un ejemplo.: 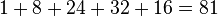$1 + 8 + 24 + 32 + 16 = 81$ , Que es igual a $3 ^ 4 = 81$ .

Yang Hui triángulo (Pascal), como se muestra por los chinos que utilizan números de la vara.

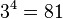Cálculo de una fila individual

Este algoritmo es una alternativa al método estándar de cálculo de células individuales con factoriales. A partir de la izquierda, el valor de la primera célula es 1. Para cada célula después, el valor se determina multiplicando el valor a la izquierda por una fracción que cambia lentamente:

$v (c) = \ frac {r-c} {c}$

Donde r = fila + 1, empezando por 0 en la parte superior, y c = la columna, empezando por 0 a la izquierda. Por ejemplo, para calcular la fila 5, r = 6. El primer valor es 1. El siguiente valor es de 1 x 5/1 = 5. Las disminuciones del numerador por uno, y el denominador aumenta en uno con cada paso. Así que 5 x 4/2 = 10. Luego de 10 x 3.3 = 10. Luego de 10 x 4.2 = 5. Entonces 5 x 1/5 = 1. Tenga en cuenta que la última celda siempre igual a 1, la multiplicación final incluida por la totalidad de la serie.

Existe un patrón similar en una diagonal hacia abajo. Comenzando con el uno y el número natural en la celda de al lado, formar una fracción. Para determinar la siguiente celda, aumentar el numerador y el denominador de cada uno, y luego multiplicar el resultado anterior por la fracción. Por ejemplo, la fila comenzando con 1 y 7 forma una fracción de 7/1. La siguiente celda es 7 x 8/2 = 28. La siguiente celda es de 28 x 9.3 = 84.

Tenga en cuenta que para cualquier fila individual sólo es necesario para calcular la mitad (redondeando hacia arriba) el número de valores en la fila. Esto es porque la fila es simétrica.

Historia

Las primeras representaciones explícitas de un triángulo de coeficientes binomiales se producen en el siglo 10 en los comentarios sobre el Chandas Shastra, un antiguo libro indio en sánscrito prosodia escrito por Pingala entre el 5ta Segundo siglos antes de Cristo. Si bien la obra de Pingala sólo sobrevive en fragmentos, el comentarista Halayudha, alrededor 975, utilizado en el triángulo para explicar oscuras referencias a Meru-prastaara, la "Escalera de Monte Meru ". También se dio cuenta de que las diagonales poco profundas de la suma triángulo a los números de Fibonacci . El matemático indio Bhattotpala (c. 1068) más tarde da filas 0-16 del triángulo.

Casi al mismo tiempo, se discute en Persia ( Irán ) por el matemático Al-Karaji (953-1029) y el poeta - astrónomo y matemático Omar Khayyam (1048-1131); por tanto, el triángulo se refiere como el "triángulo de Khayyam" en Irán . Varios teoremas relacionados con el triángulo eran conocidos, incluyendo el teorema del binomio. De hecho, podemos estar bastante seguros de que Khayyam utiliza un método de encontrar enésima raíces basadas en la expansión binomial, y por lo tanto en los coeficientes binomiales.

En el siglo 13, Yang Hui (1238-1298) presentó el triángulo aritmético, que era el mismo que el triángulo de Pascal . Hoy triángulo de Pascal se llama " Triángulo de Yang Hui "en china .

Por último, en Italia , que se conoce como "el triángulo de Tartaglia", llamado así por el algebraist italiano Niccolò Fontana Tartaglia que vivió un siglo antes de Pascal (1500-1577); Tartaglia se acredita con la fórmula general para resolver polinomios cúbicos (que puede ser realmente de Scipione del Ferro pero fue publicado por Gerolamo Cardano 1545).

Petrus Apianus (1495 -1552) publicó el Triángulo en el frontispicio de su libro sobre los cálculos de negocio 1531-1532 y una versión anterior, en 1527 el primer registro de la misma en Europa.

En 1655, Blaise Pascal escribió un triángulo arithmétique Traité du (Tratado sobre el triángulo aritmético), en el que recogió varios resultados conocidos hasta entonces sobre el triángulo, y los empleados para resolver problemas en la teoría de la probabilidad . El triángulo más tarde fue nombrado después de Pascal por Pierre Raymond de Montmort (1708) y Abraham de Moivre (1730).

Recuperado de " http://en.wikipedia.org/w/index.php?title=Pascal%27s_triangle&oldid=208833303 "