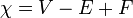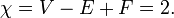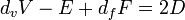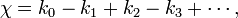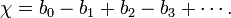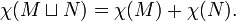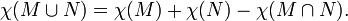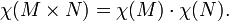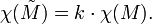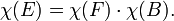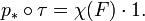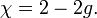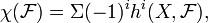Característica de Euler

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

Esta selección wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selección Wikipedia para las escuelas. Antes de decidir sobre el patrocinio de un niño, ¿por qué no aprender sobre diferentes obras de caridad de patrocinio primero ?

En matemáticas , y más concretamente en topología algebraica y combinatoria poliédrica, la característica de Euler (Euler-Poincaré o característica) es un invariante topológico, un número que describe un forma o estructura del espacio topológico, independientemente de la forma en que se dobla. Comúnmente se denota por 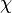$\ Chi$ ( letra griega chi).

La característica de Euler se definió originalmente para poliedros y se utiliza para probar varios teoremas sobre ellos, incluyendo la clasificación de los sólidos platónicos . Leonhard Euler , para quien el concepto se llama, fue responsable de gran parte de este trabajo temprano. En la matemática moderna, la característica de Euler surge de homología y se conecta a muchos otros invariantes.

Poliedros

La característica de Euler 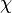$\ Chi$ fue clásicamente definido para las superficies de los poliedros, de acuerdo con la fórmula

$\ Chi = V-E + F \, \!$

donde V, E, y F son, respectivamente, los números de vértices (esquinas), y bordes se enfrenta en el poliedro dado. La superficie de cualquier poliedro convexo tiene característica de Euler

$\ Chi = V - E + F = 2. \, \!$

Este resultado se conoce como la fórmula de Euler. Esto corresponde a la característica de Euler de la esfera (que es 2), y se aplica de manera idéntica a poliedros esférica. Una ilustración de la fórmula en algunos poliedros es la siguiente.

Nombre	Vértices V	Bordes E	Caras F	Característica de Euler: V - E + F
Tetraedro	4	6	4	2
Hexahedron o cubo	8	12	6	2
Octaedro	6	12	8	2
Dodecaedro	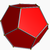20	30	12	2
Icosaedro	12	30	20	2

Las superficies de los poliedros no convexo pueden tener diversas características de Euler;

Nombre	Vértices V	Bordes E	Caras F	Característica de Euler: V - E + F
Tetrahemihexahedron	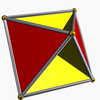6	12	7	1
Octahemioctahedron	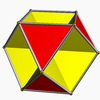12	24	12	0
Cubohemioctahedron	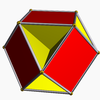12	24	10	-2
Gran icosaedro	12	30	20	2

Una forma modificada de la fórmula de Euler, usando densidad poliédrica (D) y densidad de polígono de la figuras de vértice ( 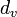$d_v$ ) Y las caras ( 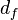$D_F$ ) Fue regalada por Arthur Cayley, y tiene tanto para los poliedros convexos (donde los factores de corrección se todo 1), y el no regular convexo Poliedros de Kepler-Poinsot:

$d_v V - E + D_F F = 2D$

Además, poliedros proyectiva todos tienen característica de Euler 1, correspondiente a la plano proyectivo real, mientras que poliedros toroidal todos tienen característica de Euler 0, correspondiente al toro .

Grafos planos

La característica de Euler se puede definir para conectado grafos planos por la misma 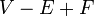$V - E + F$ como fórmula para superficies poliédricas, donde F es el número de caras en el gráfico, incluyendo la cara exterior.

La característica de Euler de cualquier grafo plano es 2. Por vía proyección estereográfica el plano se asigna a la esfera de dos dimensiones, de tal manera que los mapas gráfica para una descomposición poligonal de la esfera, que tiene característica de Euler 2. Este punto de vista está implícita en la prueba de Cauchy de la fórmula de Euler que figura a continuación.

Prueba de la fórmula de Euler

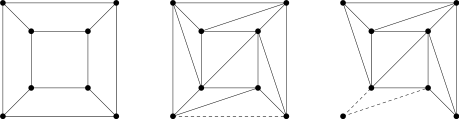
Primeros pasos de la prueba en el caso de un cubo

La primera prueba rigurosa de la fórmula de Euler, dada por Cauchy en 1811, es como sigue.

Retire una cara de la superficie poliédrica. Al tirar de los bordes de la cara que falta de distancia entre sí, deformar todo el resto en un grafo plano de puntos y curvas, como se ilustra por la primera de las tres gráficas para el caso especial del cubo. (La presunción de que la superficie poliédrica es homeomorfo a la esfera al principio es lo que hace que esto sea posible.) Después de esta deformación, las caras regulares generalmente no son regulares más. El número de vértices y aristas ha seguido siendo la misma, pero el número de caras se ha reducido en 1. Como tal, lo que demuestra la fórmula de Euler para el poliedro reduce a probar V - E + F = 1 para esto, objeto plano deformado.

Si hay una cara con más de tres lados, dibujar una diagonal, es decir, una curva a través de la cara que conecta dos vértices que no están conectados todavía. Esto añade un borde y una cara y no cambia el número de vértices, por lo que no cambia la cantidad V - E + F. Siga añadiendo bordes de esta manera hasta que todas las caras son triangulares.

Aplicar repetidamente cualquiera de las siguientes dos transformaciones:

Retirar un triángulo con sólo un borde adyacente al exterior, como se ilustra por el segundo gráfico. Esto disminuye el número de aristas y caras por uno cada uno y no cambia el número de vértices, por lo que conserva V - E + F.
Retirar un triángulo con dos bordes compartidos por el exterior de la red, como se ilustra por el tercer gráfico. Cada triángulo eliminación elimina un vértice, dos bordes y una cara, por lo que conserva V - E + F.

Repita estos dos pasos, uno tras otro, hasta que sólo queda un triángulo.

En este punto el triángulo solitario tiene V = 3, E = 3, y F = 1, de modo que V - E + F = 1. Puesto que cada uno de los dos pasos de transformación anteriores conservados esta cantidad, hemos demostrado V - E + F = 1 para el deformada, objeto plano demostrando así V - E + F = 2 para el poliedro. Esto demuestra el teorema.

Para pruebas adicionales, consulte Diecinueve Las pruebas de la Fórmula de Euler por David Eppstein. Múltiples pruebas, incluyendo sus defectos y limitaciones, se utilizan como ejemplos en Pruebas y Refutaciones por Imre Lakatos.

Definición topológica

Las superficies poliédricas discutidos anteriormente son, en lenguaje moderno, de dos dimensiones finitas CW-complejos. (Cuando sólo se usan caras triangulares, son de dos dimensiones finito complejos simpliciales). En general, para cualquier finita CW-complejo, la característica de Euler se puede definir como la suma alterna

$\ Chi = K_0 - k_1 + k_2 - k_3 + \ cdots, \$

donde k _n denota el número de células de dimensión n en el complejo.

De manera más general todavía, para cualquier espacio topológico, podemos definir el enésimo Betti número b _n como el rango de la n-ésima grupo de homología singular. La característica de Euler se puede definir como la suma alterna

$\ Chi = B_0 - b_1 + b_2 -. B_3 + \ cdots \$

Esta cantidad está bien definido si los números de Betti son finitos y si son cero más allá de un determinado índice n _0. Para los complejos simpliciales, esto no es la misma definición que en el párrafo anterior, pero un cálculo de homología muestra que las dos definiciones darán el mismo valor para 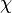$\ Chi$ .

Propiedades

Como corolario de La dualidad de Poincaré, la característica de Euler de cualquier colector y pico dimensional cerrada es cero. Esto se aplica más generalmente a cualquier compacto espacio estratificado todos cuyos estratos son impares dimensional. Además, la característica de Euler se comporta bien con respecto a muchas de las operaciones básicas sobre espacios topológicos, de la siguiente manera.

Invariancia Homotopía

Dado que la homología es un invariante topológico (de hecho, un invariante homotopy - dos espacios topológicos que son equivalentes homotopy tener isomorfo grupos de homología), por lo que es la característica de Euler.

Por ejemplo, cualquier poliedro convexo es homeomorfo al tridimensional bola, por lo que su superficie es homeomorfo (de ahí homotopy equivalente) a la bidimensional esfera , que tiene característica de Euler 2. Esto explica por qué los poliedros convexos tiene característica de Euler 2.

Principio de inclusión-exclusión

Si M y N son dos espacios topológicos, entonces la característica de Euler de su unión de la desunión es la suma de sus características de Euler, ya que la homología es aditivo bajo unión disjunta:

$\ Chi (M \ sqcup N) = \ chi (M) + \ chi (N).$

En términos más generales, si M y N son subespacios de un espacio más grande X, entonces también lo son su unión e intersección. En algunos casos, la característica de Euler obedece a una versión de la principio de inclusión-exclusión:

$\ Chi (M \ taza N) = \ chi (M) + \ chi (N) - \ chi (M \ cap N).$

Esto es cierto en los casos siguientes:

si M y N son una pareja excisive. En particular, si el interiores de M y N en el interior del sindicato todavía cubren el sindicato.

Si x es una localmente espacio compacto, y uno utiliza las características de Euler con compacto soportes, no se necesitan supuestos sobre M o N.

Si x es una espacio estratificado todos cuyos estratos son aún dimensional, el principio de inclusión-exclusión se mantiene si M y N son los sindicatos de los estratos. Esto se aplica en particular si M y N son subvariedades de un complejo variedad algebraica.

En general, el principio de inclusión-exclusión es falsa. La contraejemplo está dada por X teniendo que ser el recta real, H un subconjunto formado por un punto y el N complementar de M.

Característica del producto

Además, la característica de Euler de cualquier espacio del producto M × N es

$\ Chi (M \ N veces) = \ chi (M) \ cdot \ chi (N).$

Estas propiedades de suma y multiplicación también son disfrutados por cardinalidad de conjuntos . De esta manera, la característica de Euler se puede ver como una generalización de cardinalidad; ver .

Cubrir espacios

Del mismo modo, para un k -sheeted cubriendo el espacio 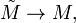$\ Tilde {H} \ a M,$ uno tiene

$\ Chi (\ tilde {H}) = k \ cdot \ chi (M).$

Más en general, para una espacio recubridor ramificada, la característica de Euler de la cubierta se puede calcular a partir de lo anterior, con un factor de corrección para los puntos de ramificación, que produce la Fórmula de Riemann-Hurwitz.

Propiedad Fibration

La propiedad del producto tiene mucho más en general, para fibraciones con ciertas condiciones.

Si 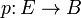$p \ dos puntos E \ a B$ es un fibración con fibra de F, con la base B path-conectado, y el fibración es orientable en un campo K, entonces la característica de Euler con coeficientes en el campo K satisface la propiedad del producto:

$\ Chi (E) = \ chi (F) \ cdot \ chi (B).$

Esto incluye espacios de productos y espacios que abarcan como casos especiales, y puede ser probada por el Sucesión espectral Serre en la homología de un fibración.

Para haces de fibras, esto también puede entenderse en términos de una mapa de transferencia 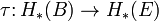$\ Tau \ dos puntos H _ * (B) \ a H _ * (E)$ - Tenga en cuenta que esta es una elevación y va "por el camino equivocado" - cuya composición con la proyección cartográfica 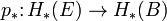$p _ * \ dos puntos H _ * (E) \ a H _ * (B)$ es la multiplicación por el Clase de Euler de la fibra:

$p_ * \ circ \ tau = \ chi (F) \ cdot 1.$

Relaciones con otros invariantes

La característica de Euler de un cerrado orientable superficie puede calcularse a partir de su género g (el número de toros en una suma descomposición conectado de la superficie; intuitivamente, el número de "manijas") como

$\ Chi = 2 -. 2 g \$

La característica de Euler de una superficie no orientable cerrado se puede calcular a partir de su género k no orientable (el número de planos proyectivos reales en una suma de descomposición de la superficie conectado) como

$\ Chi = 2 -. K \$

Para múltiples lisos cerrados, la característica de Euler coincide con el número de Euler, es decir, el Clase Euler de su fibrado tangente evalúa sobre la clase fundamental de un colector. La clase de Euler, a su vez, se refiere a todos los demás clases características de paquetes del vector.

Para cerrar Variedades de Riemann, la característica de Euler también se pueden encontrar mediante la integración de la curvatura; ver el Gauss-Bonnet teorema para el caso de dos dimensiones y la generalizada teorema de Gauss-Bonnet para el caso general.

Un análogo discreto del teorema de Gauss-Bonnet es Teorema de Descartes que el "defecto completo" de un poliedro , medida en círculos completos, es la característica de Euler del poliedro; ver defecto (geometría).

Teorema de Hadwiger caracteriza la característica de Euler como la única ( hasta multiplicación escalar) invariante por traslación, aditividad finita, la función set no-necesariamente-no negativa definida en uniones finitas de compacto convexa establece en R ⁿ que es "homogénea de grado 0".

Ejemplos

La característica de Euler se puede calcular fácilmente para superficies generales por encontrar un poligonalización de la superficie (es decir, una descripción como un CW-complejo) y usando las definiciones anteriores.

Nombre	Imagen	Característica de Euler
Intervalo		1
Círculo		0
Disco		1
Esfera		2
Toro (Producto de dos círculos)		0
Toro dobles		-2
Toro triples		-4
Plano proyectivo real		1
Cinta de Moebius		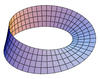0
Botella de Klein		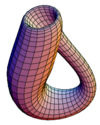0
Dos esferas (no conectado) (Unión de la desunión de dos esferas)		2 + 2 = 4
Tres esferas (no conectado) (Unión de la desunión de tres esferas)		2 + 2 + 2 = 6

Cualquier espacio contráctil (es decir, una homotopía equivalente a un punto) tiene homología trivial, lo que significa que el número de Betti 0 se encuentra en 1 y los demás 0. Por lo tanto su característica de Euler es 1. Este caso incluye el espacio euclidiano 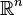$\ Mathbb {R} ^ n$ de cualquier dimensión, así como la bola unidad sólida en cualquier espacio euclidiano - el intervalo unidimensional, el disco de dos dimensiones, la pelota tridimensional, etc.

La esfera dimensional n tiene Betti número 1 en las dimensiones 0 y n, y todos los demás números de Betti 0. De ahí su característica de Euler es 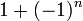$1 + (-1) ^ n$ - Esto es, ya sea 0 o 2.

El n-dimensional de bienes espacio proyectivo es el cociente de la n -sphere por el mapa antípoda. De ello se deduce que su característica de Euler es exactamente la mitad de la esfera correspondiente - ya sea 0 o 1.

El n-dimensional toro es el espacio del producto de n círculos. Su característica de Euler es 0, por la propiedad del producto. ¿Cuántos pentágonos y hexágonos Qué se necesita para hacer una Balón de fútbol? Supongamos que utilizamos 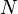$N$ hexágonos y 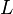$L$ pentágonos; entonces tenemos 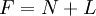$F = N + L$ enfrenta. Cada pentágono (hexágono) tiene 5 vértices (6 vértices), y cada uno es compartido entre 3 caras, por lo tanto, tenemos 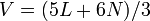$V = (5 L + 6 N) / 3$ vértices. Del mismo modo, cada pentágono (hexágono) tiene 5 bordes (6 bordes), y cada uno es compartido entre 2 caras, por lo tanto, tenemos 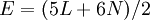$E = (5 L + 6 N) / 2$ bordes.

Desde la esfera 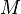$M$ tiene característica de Euler 2, debe ser que 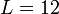$L = 12$ . El resultado es que siempre necesitamos 12 pentágonos sobre una pelota de fútbol / fútbol; el número de hexágonos es en principio ilimitada (pero para un / balón de fútbol de fútbol real, obviamente, elige un número que hace que la bola lo más esférica posible). Uno puede también aplicar este resultado a fullerenos.

Las generalizaciones

Por cada combinatoria complejo celular, uno define la característica de Euler como el número de células 0, menos el número de células 1, más el número de células 2, etc., si esta suma alterna es finito. En particular, la característica de Euler de un conjunto finito es simplemente su cardinalidad, y la característica de Euler de una gráfica es el número de vértices menos el número de bordes.

Más generalmente, se puede definir la característica de Euler de cualquier compleja cadena sea la suma alterna de la filas de los grupos de homología de la compleja cadena.

Una versión utiliza en la geometría algebraica es como sigue. Para cualquier gavilla 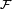$\ Scriptstyle \ mathcal {F}$ en un proyectiva esquema X, uno define su característica de Euler

$\ Chi (\ mathcal {F}) = \ Sigma (-1) ^ ih ^ i (X, \ mathcal {F}),$

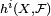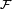donde $\ Scriptstyle h ^ i (X, \ mathcal {F})$ es la dimensión de la i-ésima grupo de cohomología gavilla de $\ Scriptstyle \ mathcal {F}$ .

Otra generalización del concepto de característica de Euler en variedades proviene de orbifolds. Mientras que cada colector tiene una característica de Euler número entero, un orbifold puede tener una característica de Euler fraccionada. Por ejemplo, el orbifold de lágrima tiene característica de Euler 1 + 1 / p, donde p es un número primo correspondiente al ángulo de cono de 2 π / p.

El concepto de Euler característico de un número finito limitado poset es otra generalización, importante en la combinatoria . Un conjunto parcialmente ordenado es "limitada" si tiene más pequeño y los elementos más grandes; llamarlos 0 y 1. La característica de Euler de un poset tales se define como el número entero μ (0,1), donde μ es el Función de Möbius en que poset de álgebra de incidencia.

Esto se puede generalizar aún más mediante la definición de un Q -valued característica de Euler para cierta finito categorías, una noción compatible con las características de Euler de gráficos, orbifolds y Posets mencionados anteriormente. En esta configuración, la característica de Euler de un finito grupo o monoide G es 1 / | G |, y la característica de Euler de un finito groupoid es la suma de 1 / | G _i |, donde recogimos un grupo representativo G _i para cada componente conectado del groupoid.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Euler_characteristic&oldid=379691924 "