Fractale


Une figure fractale ou fractale est une courbe ou surface de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques impliquant une homothétie interne. Le terme « fractale » est un néologisme créé par Benoît Mandelbrot en 1974[1]. À partir de la racine latine fractus, qui signifie brisé, irrégulier (fractale n.f.). Dans la « théorie de la rugosité » développée par Mandelbrot, une fractale désigne des objets dont la structure est invariante par changement d’échelle.
Ce terme était au départ un adjectif : les objets fractals (selon un pluriel formé sur l'exemple de « chantiers navals »). Les fractales sont définies de manière paradoxale, en référence aux structures gigognes dont ils constituent des cas particuliers : « Les objets fractals peuvent être envisagés comme des structures gigognes en tout point – et pas seulement en un certain nombre de points, les attracteurs de la structure gigogne classique. Cette conception hologigogne (gigogne en tout point) des fractales implique cette définition tautologique : un objet fractal est un objet dont chaque élément est aussi un objet fractal »[2].
Malgré les apparences, ce type de définitions de nature récursive n'est pas seulement théorique mais peut concerner aussi des concepts usuels : un ancêtre est un parent ou un ancêtre d'un parent, un multiple est un composé d'un nombre ou d'un multiple de ce nombre, un escalier commence ou prolonge un escalier, une dynastie inaugure ou prolonge une dynastie, etc.
Caractéristiques

Un objet fractal possède au moins l'une des caractéristiques suivantes :
- sa dimension de Hausdorff est strictement supérieure à sa dimension topologique. Cette caractéristique est généralement prise comme définition même d'un objet fractal. Pour exprimer la chose autrement, un réseau d'irrigation est un déploiement de lignes (« en 1D ») qui offre des caractéristiques commençant à évoquer une surface (« en 2D »). La surface du poumon (« en 2D ») est repliée en une sorte de volume (« en 3D »). De façon imagée, les fractales se caractérisent par une sorte de dimension non entière. (Mandelbrot ne considère pas cette définition comme tout à fait satisfaisante[3])
- il a des détails similaires à des échelles arbitrairement petites ou grandes ;
- il est trop irrégulier pour être décrit efficacement en termes géométriques traditionnels ;
- il est exactement ou statistiquement autosimilaire, c'est-à-dire que le tout est semblable à une de ses parties.
Domaines de validité
Les figures fractales n'ont pas à satisfaire toutes les propriétés mentionnées ci-dessus pour servir de modèles. Il leur suffit de réaliser des approximations convenables de ce qui intéresse dans un domaine de validité donné (le livre fondateur de Mandelbrot Les Objets fractals en donne une grande variété d'exemples). La taille des alvéoles du poumon, par exemple, taille à partir de laquelle celui-ci cesse de se subdiviser de façon fractale, est liée à la taille du libre parcours moyen de la molécule d'oxygène à température du corps.
La dimension utilisée est celle de Hausdorff, et on observe qu'elle correspond à une caractéristique nouvelle des surfaces irrégulières. On connait les plages de validité des dimensions de Hausdorff observées sur Terre pour les montagnes, les nuages, etc.
Des exemples de figures fractales sont fournis par les ensembles de Julia, Fatou et de Mandelbrot, la fractale de Lyapunov, l'ensemble de Cantor, le tapis de Sierpinski, le triangle de Sierpinski, la courbe de Peano ou le flocon de Koch. Les figures fractales peuvent être des fractales déterministes ou stochastiques. Elles apparaissent souvent dans l'étude des systèmes chaotiques.
Les figures fractales peuvent être réparties en trois grandes catégories :
- Les systèmes de fonctions itérées. Ceux-ci ont une règle de remplacement géométrique fixe (l'ensemble de Cantor, le tapis de Sierpinski, le triangle de Sierpinski, la courbe de Peano, le flocon de Koch) ;
- Les fractales définies par une relation de récurrence en chaque point dans un espace (tel que le plan complexe). Des exemples de ce type sont les ensembles de Mandelbrot et la fractale de Lyapunov ;
- Les fractales aléatoires, générées par des processus stochastiques et non déterministes, par exemple les paysages fractals.
De toutes ces figures fractales, seules celles construites par des systèmes de fonctions itérées affichent habituellement la propriété d'autosimilitude, signifiant que leur complexité est invariante par changement d'échelle.
Les fractales aléatoires sont les plus utilisées dans la pratique, et peuvent servir à décrire de nombreux objets extrêmement irréguliers du monde réel. Les exemples incluent des nuages, les montagnes, les turbulences de liquide, les lignes des côtes et les arbres. Les techniques fractales ont aussi été utilisées dans la compression fractale d'images, de même que dans beaucoup de disciplines scientifiques.
Dimension fractale
.jpg)
La dimension d'une ligne droite, d'un cercle et d'une courbe régulière est de 1. Une fois fixés une origine et un sens, chaque point de la courbe peut être déterminé par un nombre, qui définit la distance entre l'origine et le point. Le nombre est pris négativement s'il faut se déplacer dans le sens opposé à celui choisi au départ.
La dimension d'une figure simple dans le plan est de 2. Une fois un repère défini, chaque point de la figure peut être déterminé par deux nombres. La dimension d'un corps simple dans l'espace est de 3.
Une figure telle qu'une fractale n'est pas simple. Sa dimension n'est plus aussi facile à définir et n'est plus forcément entière. La dimension fractale, plus complexe, s'exprime à l'aide de la dimension de Hausdorff.
Quand la fractale est formée de répliques d'elle-même en plus petit, sa dimension fractale peut se calculer comme suit :
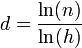
où la fractale de départ est formée de 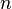 exemplaires dont la taille a été réduite d'un facteur
exemplaires dont la taille a été réduite d'un facteur 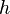 (pour homothétie).
(pour homothétie).
Quelques exemples :
- Un côté du flocon de Koch est formé de
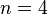 exemplaires de lui-même réduit d'un facteur
exemplaires de lui-même réduit d'un facteur 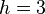 . Sa dimension fractale vaut :
. Sa dimension fractale vaut :
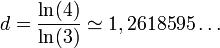
- Le triangle de Sierpinski est formé de
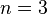 exemplaires de lui-même réduit d'un facteur
exemplaires de lui-même réduit d'un facteur 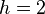 . Sa dimension fractale vaut :
. Sa dimension fractale vaut :
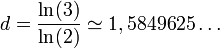
- Le tapis de Sierpinski est formé de
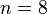 exemplaires de lui-même réduit d'un facteur
exemplaires de lui-même réduit d'un facteur 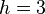 . Sa dimension fractale vaut :
. Sa dimension fractale vaut :
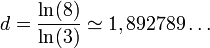
Une liste beaucoup plus longue se trouve sous : Liste de fractales par dimension de Hausdorff.
Objets fractals dans la nature


Des formes fractales approximatives sont facilement observables dans la nature. Ces objets ont une structure autosimilaire sur une échelle étendue, mais finie : les nuages, les flocons de neige, les montagnes, les réseaux de rivières, le chou-fleur ou le brocoli, et les vaisseaux sanguins.
Les arbres et les fougères sont de nature fractale et peuvent être modélisés par ordinateur à l'aide d'algorithme récursif comme les L-Systems. La nature récursive est évidente dans ces exemples ; la branche d'un arbre ou la fronde d'une fougère sont des répliques miniatures de l'ensemble : pas identiques, mais de nature similaire.
La surface d'une montagne peut être modélisée sur ordinateur en utilisant une fractale : prenons un triangle dans un espace tridimensionnel dont nous connectons les milieux de chaque côté par des segments, il en résulte quatre triangles. Les points centraux sont ensuite déplacés aléatoirement vers le haut ou le bas, dans un rayon défini. La procédure est répétée, diminuant le rayon de moitié à chaque itération. La nature récursive de l'algorithme garantit que le tout est statistiquement similaire à chaque détail.
Enfin, certains astrophysiciens ont remarqué des similitudes dans la répartition de la matière dans l'Univers à six échelles différentes. Les effondrements successifs de nuages interstellaires, dus à la gravité, seraient à l'origine de cette structure (partiellement) fractale. Ce point de vue a donné naissance au modèle de l'univers fractal, décrivant un univers fondé sur les fractales.
Domaines d'application
Les domaines d'application des fractales sont très nombreux, on peut citer en particulier[4] :
- en biologie, répartition des structures des plantes, bactéries, feuilles, branches d'arbres…
- en géologie, étude du relief, côtes et cours d'eau, structures de roches, avalanches…
- en paléontologie, loi de puissance des apparitions et extinctions d'espèces
- en morphologie animale, structures des invertébrés, plumes d'oiseaux…
- en médecine, structure des poumons, intestins, battements du cœur
- en météorologie, nuages, vortex, banquise, vagues scélérates, turbulences, structure de la foudre
- en volcanologie, prévision d'éruptions volcaniques, tremblements de terre
- en astronomie avec la description des structures de l'univers, cratères sur la Lune, répartition des exoplanètes et des galaxies…
- en sciences humaines, structure urbaine, évolution de la démographie
- en économie et finance, prévision des krachs boursiers (théorie des fractales)
- en électronique, antennes larges bandes des téléphones portables
- dans les arts, art graphiques bien sûr, mais aussi en littérature, en musique, au cinéma…
Tous ces domaines - et bien d'autres - peuvent bénéficier de la description et d'une modélisation en termes fractals des phénomènes associés.
Le modèle commence[Quand ?] tout particulièrement à se développer en finance, où l'approche fractale de Mandelbrot se prête aux marchés volatils. Des sociétés utilisent un modèle identifiant les répétitions mathématiques afin de prévoir certains mouvements de prix à court-terme. Cette approche systématique est basée sur la volatilité et l'accélération des échanges de titres afin de valider les tendances. Une anticipation des variations est ainsi immédiatement inscrite sur le modèle : si la variation est d'ampleur suffisante, elle permet de prendre par exemple une position short[Quoi ?] sur le marché.
Galerie d'images
-

Ensemble de Mandelbrot
-
.png)
Ensemble de Julia en
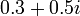
-
.jpg)
L'éponge de Menger
-

Suite qui tend vers le flocon de Koch
Informatique
- Fractint est un logiciel gratuit destiné à tracer de nombreux types de fractales.
- Sterling est un générateur de fractales gratuit pour Windows.
- XaoS est un logiciel libre permettant une découverte à la fois technique et poétique des fractales.
- Qosmic est un logiciel s'intéressant à l'édition de flammes fractales, les rendus sont générés de manière algorithmique.
- Méthodes informatiques de calcul
- Système de fonctions itérées (IFS).
- Jeu du chaos
- Système de Lindenmayer ou L-System.
- Méthodes topologiques.
- Algorithme Diamant-Carré
Utilisations industrielles
Surface spécifique de Blaine : la finesse de broyage d'un ciment est exprimée en termes de surface spécifique (cm²/g) et mesurée par la méthode de Blaine, dite de perméabilité à l'air, utilisant la loi de Darcy, et la loi de Kozeny-Carman qui établit que la traversée d'un lit de granules par un fluide est affectée par la surface spécifique des granules. Ainsi, en calculant la durée que met un gaz sous pression à traverser un volume donné de granules, on en déduit la surface des granules. Plus le broyage est fin, plus la surface calculée est importante. Cette expérience se produisant dans un volume déterminé, on peut imaginer obtenir une surface développée infinie en broyant toujours plus finement le ciment. Il s'agit là d'une utilisation industrielle d'un modèle expliqué par les mathématiques fractales (un objet de dimension 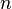 de mesure finie, borné par une frontière de dimension
de mesure finie, borné par une frontière de dimension 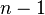 , de mesure tendant vers l'infini).
, de mesure tendant vers l'infini).
Notes et références
- ↑ 50 ans après Einstein un savant élucide les mystères de l'univers, Sciences et vie, n°936, septembre 1995, page 51.
- ↑ Le Trésor des Paradoxes, Philippe Boulanger et Alain Cohen, Éd. Belin, 2007.
- ↑ Benoît Mandelbrot, Fractales, hasard et finance, Flammarion, coll. « Champs sciences » (réimpr. 2009) (1re éd. 1997), 246 p. (ISBN 978-2-0812-2510-7), chap. 1.3 (« Principes d'échelle, distributions scalantes, dimensions fractales, et H »), p. 56 :
« Il est vrai que [mes textes de 77 et de 82] avaient eu l'imprudence de proposer, pour le concept de fractale, une « définition pour voir », ou « définition tactique ». Ses défauts majeurs, vite apparus, me l'ont fait retirer dès le deuxième tirage [du texte de 82]. Mais elle persiste à être citée et à inquiéter. Je disais donc que l'ensemble E est fractal si […]
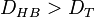 . »
. » - ↑ Le monde des fractales, Jacques Dubois & Jean Chaline
Annexes
Bibliographie
- (en) Kenneth Falconer (en), Fractal Geometry, 1990, John Wiley & Sons (ISBN 0-471-92287-0).
- (en) Benoît Mandelbrot, The Fractal Geometry of Nature, 1982, W. H. Freeman (en) (ISBN 0-7167-1186-9). Trad. : Les objets fractals. Forme, chance et dimension, Flammarion, 2e éd. 1984.
- (en) Heinz-Otto Peitgen (de), The Science of Fractal Images, 1988, Springer (ISBN 0-387-96608-0).
- (en) Heinz-Otto Peitgen, Fractals for the classroom, New York, Springer, 1993.
- (en) Michael Barnsley (en), Fractals Everywhere, Morgan Kaufmann (en) (ISBN 0-12-079061-0)
- Bernard Sapoval, Universalités et fractales, Flammarion, coll. Champs.
- Jacques Dubois et Jean Chalin, Le monde des fractales, 2006, Éditions Ellipses (ISBN 978-2-7298-2782-3).
- André Dauphiné, Géographie fractale, Hermès-Lavoisier, 2011 (ISBN 978-2-7462-3798-8)
Articles connexes
- Benoît Mandelbrot (biographie, et historique de sa découverte)
- Théorie constructale
- Dimension de Hausdorff
- Déterminisme
- Liste de fractales par dimension de Hausdorff
- Récursivité
- Modèle christallérien
- Pavage de Penrose
- Relativité d'échelle
- Univers fractal
- Mission fractale, nouvelle de science-fiction de Michel Jeury (1980)
- Mise en abyme
Liens externes
- (en) Benoit Mandelbrot, Cours sur les fractales
- Catégorie chaos et fractales de l’annuaire DMOZ
- Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal (fractales en 3D)
- Zoom Video au cœur d'un Mandelbox(Exemple de fractale 3D)
- Portail de la géométrie