Perméabilité (fluide)

Pour les articles homonymes, voir Perméabilité.

Cet article est une ébauche concernant la mécanique des fluides.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

La perméabilité d'un matériau (une roche, un tissu, etc.) correspond à son aptitude à se laisser traverser par un fluide de référence sous l'effet d'un gradient de pression.

La perméabilité $k$ s'exprime généralement en Darcy (D). Un darcy correspond à la perméabilité d'un corps continu et isotrope au travers duquel un fluide de viscosité équivalente à celle de l'eau à 20 °C s'écoule à une vitesse de 1 cm·s^-1 lorsqu'il est soumis à une pression de 1 atm, ce qui correspond à la dimension d'une surface. 1 D = 0,97×10^-12 m²

Le terme de conductivité hydraulique (ou coefficient de perméabilité $K$ ) est le rapport entre cette perméabilité et la viscosité du fluide (généralement le fluide est l'eau). Plus un milieu est perméable plus le fluide s'écoulera vite. La conductivité hydraulique s'exprime en m⋅s^-1. La conversion suivante^{[réf. insuffisante]} est disponible pour l'eau : 10^-12 cm⋅s^-1 ≘ 10^-19 m² ≃ 10^-7 D.

Aspects théoriques

La perméabilité se manifeste à deux échelles. L'aspect macroscopique, la perméabilité d'un matériau entraîne une perte de charge lors de l'écoulement d'un fluide au travers de ce dernier. Cette perte de charge se calcule au travers de la loi de Darcy:

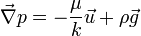
$\vec{\nabla}p=-\frac{\mu}{k}\vec{u}+\rho\vec{g}$

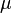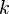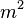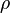où $\mu$ est la viscosité du fluide( $Pa.s$ ), $\vec{\nabla}p$ la perte de charge, $k$ la permeabilité ( $m^{2}$ ) et $\rho$ la masse volumique du fluide. Dans cette équation, la vitesse 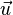$\vec{u}$ n'est pas la vitesse réelle du fluide. Il s'agit de la vitesse de Darcy. Cette dernière est reliée au débit et à l'aire totale d'une section (perpendiculaire au flux) du matériau 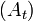$(A_t)$ , ainsi qu'à la vitesse réelle (interstitielle) au travers de la porosité du matériau $\Phi$ .

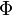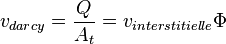
$v_{darcy}=\frac{Q}{A_t}=v_{interstitielle} \Phi$

La porosité est l'expression du rapport du Volume de vide (pores) sur le volume total du matériau considéré. Une perméabilité élevée exige une bonne porosité mais l'inverse n'est pas vrai. Une roche très poreuse peut avoir une perméabilité très faible (argiles par exemple). Ce genre de phénomènes trouve son explication au travers de l'équation de Kozeny-Carman. Cette dernière relie la perméabilité à la porosité du matériau au travers de grandeurs statistiques décrivant la géométrie et la répartition des pores^[1].

Elle ne doit pas être confondue non plus avec la capacité d'absorption d'une matière.

Mesure de la perméabilité

Il n'est pas simple de mesurer la perméabilité. C'est une grandeur statistique du matériau. On peut la comparer à une vitesse d'infiltration et dans ce cas, la mesure peut être réalisée avec un infiltromètre. Cette mesure repose sur deux essais normalisés : l’essai de pompage (qui repose sur la formule de Dupuit) et l’essai Lefranc, qui, comme l’essai Porchet, est au fond un essai d’infiltration.

Imperméabilité

L'imperméabilité, notion inverse de la perméabilité, s'emploie plus couramment dès lors qu'il s'agit d'objets usuels. Le terme s'applique notamment aux matières en contact épisodique mais régulier avec l'eau, par exemple pour désigner la capacité des tissus ou des façades de bâtiments à empêcher la pénétration de l'eau de pluie. Il ne doit pas être confondu avec la déperlance. L'argile, par exemple, est une roche imperméable. On utilise aussi ce terme pour parler de la capacité à empêcher le passage de l'air ou de poussières.

Notes et références

↑ (en) Jun Feng Wang, « Permeability Prediction of Fibrous Porous Media in a Bi-Periodic Domain », Journal of Composite Materials, SAGE Publications, vol. 42,‎ 2008, p. 909

Articles connexes

Porosité
Capacité d'absorption
Étanchéité
Méthode de séparation membranaire
Loi de Darcy

Portail de la physique