Jeu de la vie

"Conway jeu" peut se r??f??rer ?? des jeux tel que d??fini par num??ros surr??alistes, qui Conway a ??galement d??velopp??.

Planeur Gun Gosper cr??ation " planeurs ".

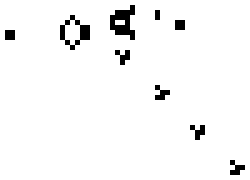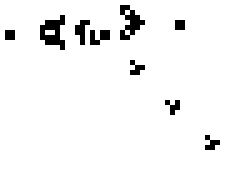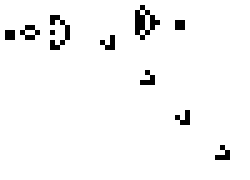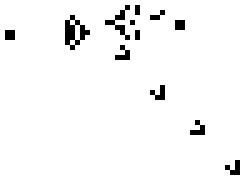
The Game of Life est un automate cellulaire imagin?? par la Colombie- math??maticien John Horton Conway en 1970. Ce est l'exemple le plus connu d'un automate cellulaire.

Le ??jeu?? est en fait un z??ro-joueurs, ce qui signifie que son ??volution est d??termin?? par son ??tat initial, ne n??cessitant aucune entr??e de joueurs humains. On interagit avec le jeu de la vie en cr??ant une configuration initiale et en observant comment il ??volue. Une variante existe lorsque deux joueurs se affrontent.

R??gles

L'univers du jeu de la vie est un infini grille orthogonale bidimensionnelle de cellules carr??es, dont chacun est dans l'un des deux ??tats possibles, vivants ou morts. Chaque cellule interagit avec ses huit voisins, qui sont les cellules qui sont directement horizontalement, verticalement ou en diagonale adjacente. A chaque ??tape de temps, les transitions suivantes se produisent:

1. Toute cellule vivante avec moins de deux voisins vivants meurt, comme si par la solitude.
2. Toute cellule vivante avec plus de trois voisines vivantes meurt, comme si par la surpopulation.
3. Toute cellule vivante avec deux ou trois voisines vivantes vit, inchang??e, ?? la prochaine g??n??ration.
4. Toute cellule morte avec exactement trois voisins vivants vient ?? la vie.

Le motif initial constitue la ??graine?? du syst??me. La premi??re g??n??ration est cr????e en appliquant les r??gles ci-dessus simultan??ment ?? chaque cellule dans la graine - naissances et d??c??s se produisent simultan??ment, et le moment discr??te ?? laquelle cela se produit est parfois appel?? une tique. (En d'autres termes, chaque g??n??ration est une fonction pure de la pr??c??dente.) Les r??gles continuent ?? ??tre appliqu?? plusieurs fois pour cr??er de nouvelles g??n??rations.

Origines

Conway se est int??ress?? ?? un probl??me pr??sent?? dans les ann??es 1940 par le math??maticien de renom John von Neumann , qui a essay?? de trouver une machine hypoth??tique qui pourrait construire des copies de lui-m??me et a r??ussi quand il a trouv?? un mod??le math??matique pour une telle machine avec des r??gles tr??s compliqu??es sur une grille rectangulaire . Conway a essay?? de simplifier les id??es de von Neumann et a finalement r??ussi. En couplant son succ??s pr??c??dent avec Le probl??me de Leech en th??orie de groupe avec son int??r??t pour les id??es de von Neumann sur les appareils de l'auto-r??plication, Conway a con??u le jeu de la vie.

Il a fait sa premi??re apparition publique dans le num??ro d'Octobre 1970 Scientific American, dans Martin Gardner " Jeux Math??matiques "colonne. D'un point de vue th??orique, il est int??ressant, car il a le pouvoir d'un machine de Turing universelle: ce est tout ce qui peut ??tre calcul??e par algorithme peut ??tre calcul?? ?? l'int??rieur Jeu de la vie. Gardner a ??crit:

Le jeu fait Conway instantan??ment c??l??bre, mais il a ??galement ouvert un nouveau champ de la recherche math??matique, le domaine de la automates cellulaires ... Parce que des analogies de la vie avec la mont??e, la chute et des alt??rations d'une soci??t?? d'organismes vivants, il appartient ?? une classe de plus en plus de ce qu'on appelle ??jeux de simulation?? (jeux qui ressemblent ?? des processus de la vie r??elle)

Depuis sa publication, Jeu de la vie a suscit?? beaucoup d'int??r??t en raison des moyens surprenants dans laquelle les mod??les peuvent ??voluer. La vie est un exemple de ??mergence et auto-organisation. Il est int??ressant pour les physiciens , biologistes , ??conomistes , math??maticiens , philosophes , g??n??ratives scientifiques et autres ?? observer la fa??on dont les mod??les complexes peuvent ??merger de la mise en ??uvre des r??gles tr??s simples. Le jeu peut aussi servir comme une didactique analogie, utilis?? pour transmettre la notion quelque peu contre-intuitif que ??la conception?? et ??organisation?? peuvent ??merger spontan??ment en l'absence d'un designer. Par exemple, philosophe et scientifique cognitive Daniel C. Dennett a utilis?? l'analogue de la vie "l'univers" de Conway largement pour illustrer l'??volution possible des constructions philosophiques complexes, tels que conscience et le libre arbitre, de l'ensemble relativement simple des lois physiques r??gissant d??terministes notre propre univers.

La popularit?? de la vie de Conway a ??t?? aid?? par le fait qu'il a vu le jour juste ?? temps pour une nouvelle g??n??ration de peu co??teuse mini-ordinateurs qui ont ??t?? lib??r??s dans le march??, ce qui signifie que le jeu pourrait ??tre ex??cut?? pendant des heures sur ces machines qui ??taient par ailleurs utilis?? la nuit. ?? cet ??gard, il pr??figure la popularit?? ult??rieure de g??n??r??es par ordinateur fractales . Pour beaucoup, la vie ??tait tout simplement un d??fi de programmation, une fa??on amusante de perdre CPU cycles. Pour certains, cependant, la vie a des connotations plus philosophiques. Il se est d??velopp?? un v??ritable culte dans les ann??es 1970 et au-del??; d??veloppements actuels ont ??t?? jusqu'?? cr??er des ??mulations th??oriques de syst??mes informatiques dans les limites d'un conseil de vie.

Conway a choisi ses r??gles attentivement, apr??s beaucoup d'exp??rimentation, pour r??pondre ?? trois crit??res:

1. Il devrait y avoir aucun mod??le initial pour lequel il ya une simple preuve que la population peut cro??tre sans limite.
2. Il devrait y avoir des motifs initiaux qui, apparemment, ne poussent sans limite.
3. Il devrait y avoir des motifs simples initiales qui se d??veloppent et changent pour une p??riode de temps consid??rable avant de venir ?? sa fin dans les fa??ons possibles suivantes:

   • Estomper compl??tement (de la surpopulation ou de devenir trop rares); ou
   • Installation dans une configuration stable qui reste inchang?? par la suite, ou d'entrer dans une phase d'oscillation dans laquelle ils r??p??tent un cycle sans fin de deux ou plusieurs p??riodes.

Des exemples de motifs

L'??volution et le mouvement d'un planeur.

L'??volution et le mouvement d'un LWSS.

De nombreux types de mod??les diff??rents se produisent dans le jeu de la vie, y compris les patrons statiques (" natures mortes ??), motifs r??p??titifs (" oscillateurs "- un sur-ensemble de natures mortes), et des motifs qui se traduisent ?? travers le conseil d'administration (" vaisseaux spatiaux "). Les exemples les plus courants de ces trois classes sont indiqu??es ci-dessous, avec des cellules vivantes apparaissent en noir, et les cellules mortes apparaissent en blanc.

Block (nature morte)
Bateau (nature morte)
Clignotant (deux phases oscillateur)
Toad (deux phases oscillateur)
Planeur (vaisseau spatial)
Vaisseau spatial (Lightweight LWSS)
Pulsar (triphas?? oscillateur)

Le "pulsar" est la p??riode 3 oscillateur le plus commun. La grande majorit?? des oscillateurs sont naturellement p??riode de 2, comme le clignotant et le crapaud, mais les p??riodes 4, 8, 15, 30, et quelques autres ont ??t?? vus en de rares occasions .

Patterns appel??s " Mathusalems "peut ??voluer pendant de longues p??riodes avant de r??p??ter." Diehard "est un mod??le qui finit par dispara??tre apr??s 130 g??n??rations, ou des ??tapes." Acorn "prend 5,206 g??n??rations ?? g??n??rer au moins 25 planeurs et stabiliser autant oscillateurs.

Diehard	Gland

Conway origine conjectur?? qu'aucun motif peut cro??tre ind??finiment - ce est ?? dire, que pour toute configuration initiale avec un nombre fini de cellules vivantes, la population ne peut pas d??passer une certaine limite sup??rieure finie. En apparence originale du jeu dans " Jeux math??matiques ", Conway a offert un prix de 50 $ ?? la premi??re personne qui pourrait prouver ou de r??futer la conjecture avant la fin de 1970. Une fa??on de r??futer serait de d??couvrir des mod??les qui maintiennent compteurs ajoutant au champ: un?? pistolet ??, qui serait une configuration qui tire ?? plusieurs reprises de d??placer des objets tels que le ??planeur??, ou un ??train de pompe??, ce qui serait une configuration qui se d??place, mais laisse derri??re lui une tra??n??e de "fum??e" persistante.

Le prix a ??t?? remport?? en Novembre de la m??me ann??e par une ??quipe de la Massachusetts Institute of Technology, dirig?? par Bill Gosper; le ??pistolet Gosper" ci-dessous produit son premier planeur sur la 15e g??n??ration, et un autre planeur chaque 30e g??n??ration ?? partir de l??. Ce premier coup de canon de parapente est toujours le plus petit connu:

Mod??les simples ont ??t?? plus tard constat?? que la pi??ce ??galement la croissance infinie. Les trois mod??les suivants cro??tre ind??finiment: les deux premiers cr??er un moteur ??de bloc portant" switch chacun, tandis que le troisi??me cr??e deux. La premi??re n'a que 10 cellules vivantes (qui a ??t?? prouv?? pour ??tre minime). La seconde tient dans un carr?? de 5 ?? 5. La troisi??me est une seule cellule haute:

D??couvertes ult??rieures inclus d'autres " armes ", qui sont fixes et jaillissent planeur ou d'autres vaisseaux spatiaux;" inhalateurs ??, qui se d??placent le long laissant derri??re lui une tra??n??e de d??bris, et" r??teaux ", qui se d??placent et ??mettre des vaisseaux spatiaux. Gosper a ??galement construit le premier mod??le avec un asymptotiquement optimal taux de croissance quadratique, appel?? " obtenteur ", ou" homard ", qui a travaill?? en laissant derri??re lui une tra??n??e de pistolets.

Il est possible pour les planeurs d'interagir avec d'autres objets de mani??re int??ressante. Par exemple, si deux planeurs sont tourn??s en un bloc dans la bonne fa??on, le bloc se rapprocher de la source des planeurs. Si trois planeurs sont tir?? une balle dans la bonne fa??on, le bloc se d??place plus loin. Cette ??m??moire de bloc coulissant" peut ??tre utilis??e pour simuler un compteur. Il est possible de construire des portes logiques tels que ET, OU et PAS utilisant planeurs. Il est possible de construire un mod??le qui se comporte comme un machine ?? ??tats finis connect?? ?? deux compteurs. Cela a la m??me puissance de calcul comme un Machine de Turing universelle, de sorte que le jeu de la vie est aussi puissant que ne importe quel ordinateur avec une m??moire illimit??e: il est Turing complet. En outre, un mod??le peut contenir une collection d'armes ?? feu qui se combinent pour construire de nouveaux objets, y compris des copies du mod??le original. Un "constructeur universel" peut ??tre construit qui contient un ordinateur complet de Turing, et qui peut construire de nombreux types d'objets complexes, y compris plus de copies de lui-m??me.

It??ration

D'un motif initial al??atoire de cellules vivantes sur la grille, les observateurs trouveront la population en constante ??volution que les g??n??rations se ??gr??nent. Les tendances qui se d??gagent des r??gles simples peuvent ??tre consid??r??s comme une forme de beaut??. Petits sous-masques isol??s sans sym??trie initiale ont tendance ?? devenir sym??triques. Une fois que cela se produit la sym??trie peut augmenter la richesse, mais il ne peut pas ??tre perdu si un sous-motif voisine est assez proche de la troubler. Dans de tr??s rares cas, la soci??t?? finit par mourir sur, avec toutes les cellules vivantes en voie de disparition, mais cela peut ne pas se produire pour un grand nombre de g??n??rations. La plupart des mod??les initiaux ??ventuellement ??burn out??, soit la production de chiffres ou des motifs qui oscillent toujours entre deux ou plusieurs ??tats stables; plusieurs produisent aussi un ou plusieurs planeurs ou des vaisseaux spatiaux qui voyagent ind??finiment loin de l'emplacement initial.

Algorithmes

Conway a d??couvert que le F- pentomino ??chou?? ?? se stabiliser dans un petit nombre de g??n??rations.

Les premiers r??sultats dans le jeu de la vie ont ??t?? obtenus sans l'utilisation des ordinateurs. Les simples natures mortes et les oscillateurs ont ??t?? d??couverts tout en suivant le sort de diff??rents petites configurations de d??part ?? l'aide de papier millim??tr??, tableaux noirs, des plateaux de jeux physiques (telles que Go ) et similaires. Au cours de ces premi??res recherches, Conway a d??couvert que le F- pentomino (qu'il appelle le ??R-pentomino") n'a pas r??ussi ?? se stabiliser dans un petit nombre de g??n??rations.

Ces d??couvertes inspir??es programmeurs informatiques dans le monde entier d'??crire des programmes pour suivre l'??volution des modes de vie. La plupart des premiers algorithmes ??taient similaires. Ils repr??sentaient les modes de vie comme des tableaux en deux dimensions dans la m??moire de l'ordinateur. Typiquement deux tableaux sont utilis??s, l'un pour tenir la g??n??ration actuelle et celle dans laquelle pour calculer son successeur. Souvent 0 et 1 repr??sentent les cellules mortes et vivantes, respectivement. Une double boucle consid??re chaque ??l??ment de la gamme actuelle ?? son tour, en comptant les voisins en direct de chaque cellule de d??cider si l'??l??ment correspondant de la matrice successeur devrait ??tre 0 ou 1. Le tableau successeur se affiche. Pour la prochaine it??ration les tableaux changer de r??le pour que la matrice de successeur dans la derni??re it??ration devient la gamme actuelle dans la prochaine it??ration.

Une vari??t?? d'am??liorations mineures ?? ce sch??ma de base sont possibles, et il ya plusieurs fa??ons d'??conomiser de calcul inutile. Une cellule qui n'a pas chang?? ?? la derni??re ??tape de temps, et dont aucun des voisins chang??, est garanti de ne pas changer ?? l'??tape de l'heure ainsi, donc un programme qui garde la trace des zones sont actives peut gagner du temps en ne mettant ?? jour le zones inactives.

En principe, le domaine de La vie est infinie, mais les ordinateurs ont de la m??moire finie, et g??n??ralement la taille des tableaux doit ??tre d??clar??e ?? l'avance. Cela conduit ?? des probl??mes lors de la surface active empi??te sur la fronti??re de la matrice. Les programmeurs ont utilis?? plusieurs strat??gies pour r??soudre ces probl??mes. La strat??gie la plus simple consiste simplement ?? supposer que chaque cellule en dehors de la gamme est mort. Ce est facile ?? programmer, mais conduit ?? des r??sultats inexacts lorsque la zone active traverse la fronti??re. Un truc plus sophistiqu??e consiste ?? examiner les bords gauche et droit du champ pour ??tre cousues ensemble, et les bords sup??rieur et inf??rieur aussi, donnant un toro??dal tableau. Le r??sultat est que des zones actives qui se d??placent ?? travers une ar??te de champ r??apparaissent au niveau du bord oppos??. Impr??cision peut encore aboutir si le motif devient trop importante, mais au moins il n'y a pas des effets de bord pathologiques. Techniques d'allocation de stockage dynamique peuvent ??galement ??tre utilis??s, cr??ant toujours plus grands tableaux de tenir mod??les de croissance.

Alternativement, le programmeur peut abandonner la notion de repr??senter le domaine de la vie avec un tableau ?? 2 dimensions, et d'utiliser une structure de donn??es diff??rente, comme un vecteur de paires de coordonn??es repr??sentant des cellules vivantes. Cette approche permet de d??placer le motif sur le terrain sans entrave, tant que la population ne d??passe pas la taille de la matrice de coordonn??es direct. L'inconv??nient est que le comptage voisines vivantes devient une op??ration de recherche, ce qui ralentit la vitesse de simulation. Avec des structures de donn??es plus sophistiqu??es ce probl??me peut ??galement ??tre en grande partie r??solu.

Pour explorer de grands motifs ?? de grandes profondeurs de temps, des algorithmes sophistiqu??s comme Hashlife peut ??tre utile.

Variations sur la vie

Depuis sa cr??ation originale de la vie, de nouvelles r??gles ont ??t?? ??labor??es. Le jeu standard de vie, dans lequel une cellule est "n??" si elle a exactement trois voisins, reste en vie si elle a 2 ou 3 voisins vivant, et meurt autrement, est symbolis??e par "23/3". Le premier num??ro, ou liste de nombres, est ce qui est n??cessaire pour une cellule de continuer. La deuxi??me s??rie est l'exigence de la naissance. Ainsi ??16/6?? signifie ??une cellule est n?? se il ya six voisins, et vit sur se il ya 1 ou six voisins??. HighLife est 23/36, parce qu'avoir six voisins, en plus de 23/3 r??gle du jeu original, provoque une naissance. HighLife est surtout connu pour ses r??plicateurs. D'autres variantes existent sur la vie, bien que la grande majorit?? de ces univers sont soit trop chaotique ou d??sol??e.

Un ??chantillon d'un oscillateur 48 ??tapes ?? partir d'un jeu 2D hexagonale de la vie (r??gle 34/2).

Certaines variations de modifier la g??om??trie de l'univers ainsi que la r??gle. Les variations ci-dessus peuvent ??tre consid??r??s comme 2D Square, parce que le monde est ?? deux dimensions et mis en une grille carr??e. Place 3D et 1D carr??s variantes ont ??t?? d??velopp??es, comme l'ont fait les variations 2D hexagonales o?? le r??seau est hexagonale ou triangulaire au lieu de la place.

Les r??gles de Conway peuvent ??galement ??tre g??n??ralis??s de sorte qu'au lieu de deux Etats (vivantes et mortes) il ya trois ou plus. Les transitions d'??tat sont ensuite d??termin??s soit par un syst??me de pond??ration, soit par une table sp??cifiant les r??gles de transition distinctes pour chaque ??tat; par exemple, Multicolore "R??gles Tableau" de Cellebration de Mirek et les familles de la r??gle "de vie pond??r??e" comprennent chacun exemples de r??gles ??quivalentes ?? la vie de Conway.

Patterns relatives aux fractales et syst??mes fractales peuvent ??galement ??tre observ??s dans certaines variations de la vie comme. Par exemple, l'automate 12/1 g??n??re quatre approximations tr??s proche de la Triangle Sierpiński lorsqu'il est appliqu?? ?? une seule cellule vivante.

L'immigration est une variation qui est le m??me que le jeu de la vie, sauf qu'il ya deux ??tats ON (souvent exprim?? en deux couleurs diff??rentes). Chaque fois qu'une nouvelle cellule est n??, il prend l'??tat ON qui est la majorit?? dans les trois cellules qui lui ont donn?? naissance. Cette fonction peut ??tre utilis??e pour examiner les interactions entre vaisseaux spatiaux et autres ??objets?? dans le jeu. Une autre variante similaire, appel?? QuadLife, implique quatre diff??rents ??tats ON. Quand une nouvelle cellule est n??e de trois diff??rents sur les voisins, il prend la quatri??me valeur, et par ailleurs, comme l'immigration, il prend la valeur de la majorit??. ?? l'exception de la variation entre les cellules ON, ces deux variations agissent de mani??re identique ?? la Vie.

Variante pour deux joueurs

Dans cette variante, les cellules vivantes peuvent avoir deux couleurs et un joueur gagne quand toutes les cellules de la couleur de l'adversaire sont ??limin??s. Quand une cellule morte devient en direct, sa couleur est d??termin??e par la couleur dominante de ses cellules vivantes voisins (qui sont exactement trois), comme dans l'immigration pr??cit??e. Commencez avec un mod??le d??part al??atoire ou pr??-choisie avec la moiti?? des cellules vivantes de chaque couleur. Apr??s une it??ration, le premier joueur peut ajouter une cellule de sa couleur et de supprimer une cellule de la couleur de son adversaire. Apr??s la prochaine it??ration de l'autre joueur peut faire la m??me chose, et ainsi de suite.

Programmes de vie notables

Le premier programme de vie a ??t?? ??crit pour le PDP-7 par Guy et MJT SR Bourne en 1970. Sans son aide quelques d??couvertes sur le jeu aurait ??t?? difficile ?? faire.

Il ya maintenant des milliers de programmes de la vie en ligne, donc la liste compl??te ne seront pas fournis ici. Ce qui suit est une s??lection d'un petit nombre de programmes avec une certaine r??clamation particuli??re ?? la notabilit??, comme la popularit?? ou des caract??ristiques inhabituelles. La plupart de ces programmes int??grent une interface utilisateur graphique pour l'??dition de sch??mas et la simulation, la capacit?? de simuler de multiples r??gles, y compris la vie, et une grande biblioth??que de motifs int??ressants dans la vie et d'autres r??gles de CA.

• Jeu de la vie par Alan Hensel. Une applet Java Web de pop-up avec des algorithmes de simulation rapides et une grande biblioth??que de mod??les de vie int??ressante.
• Golly. Un multi-plateforme (Windows, Macintosh et Linux) open-source syst??me de simulation de vie par Andrew Trevorrow et Tomas Rokicki y compris le algorithme de Hashlife pour la production extr??mement rapide et Python scriptabilit?? ?? la fois pour l'??dition et la simulation.
• Life32. Freeware pour les machines Windows inclut de puissantes et scriptable fonctions d'??dition de motif.
• La Cellebration de Mirek. 1-D et 2-D automates cellulaires visionneuse gratuite, explorateur et ??diteur pour Windows. Comprend les installations puissants de simulation et d'affichage d'une grande vari??t?? de r??gles CA y compris la vie, et un ??diteur de scripts.
• Xlife Un laboratoire cellulaire-automate par Jon Bennett. Longtemps l'application standard de simulation Vie Linux, il a ??galement ??t?? port?? sur Windows. Peut g??rer des r??gles d'automates cellulaires avec le m??me quartier que la vie et jusqu'?? huit ??tats possibles par cellule. Voir ici depuis de nombreuses versions alternatives.