Absolutamente nada

El cero absoluto es la m??s baja posible la temperatura en la que nada podr??a ser m??s fr??o, y sin calor de energ??a permanece en una sustancia. El cero absoluto es el punto en el que las mol??culas no se mueven (en relaci??n con el resto del cuerpo) m??s de lo que se requiere que por una mec??nica cu??ntica efecto llamado energ??a de punto cero. Es un l??mite te??rico y no se puede lograr.

Por acuerdo internacional, el cero absoluto se define como, precisamente, 0 K en el Kelvin escala, que es un (absoluta) temperatura termodin??mica escala y -273,15 ?? C en el Celsius escala (cent??grados). El cero absoluto tambi??n es precisamente equivalente a 0 ?? R en el Escala Rankine (tambi??n una escala de temperatura termodin??mica), y -459,67 ?? F en el Escala Fahrenheit. Aunque no es posible enfriar cualquier sustancia a 0 K, los cient??ficos han hecho grandes avances en el logro de las temperaturas cercanas al cero absoluto, donde exhibe la materia efectos cu??nticos tales como la superconductividad y superfluidez. De hecho, en 2000 la Universidad Tecnol??gica de Helsinki inform?? que alcanzan temperaturas de 100 pK (1 ?? 10 ^-10 K).

Historia

Uno de los primeros en hablar de la posibilidad de un "fr??o absoluto" en una escala tal fue Robert Boyle quien en sus 1.665 nuevos experimentos y observaciones que tocan Fr??a, declar?? la disputa que es el frigidum primum es muy conocido entre los naturalistas, algunos contender por la tierra, otros para el agua, otros por el aire, y algunos de los modernos para nitro, pero todos parec??an estar de acuerdo en que:

Limite el 'grado de fr??o "

La cuesti??n de si existe un l??mite en el grado de fr??o posible, y, si es as??, d??nde se debe colocar el cero, fue atacado por primera vez por el f??sico franc??s Guillaume Amontons en 1702, en relaci??n con sus mejoras en el term??metro de aire y en sus temperaturas de instrumentos fueron indicados por la altura a la que una columna de mercurio fue sostenido por una cierta masa de aire, el volumen o el "resorte" que por supuesto var??a con el calor al que se expone. Por lo tanto, Amontons argumentaron que el cero de su term??metro ser??a la temperatura a la que el resorte del aire en ella se redujo a nada. En la escala que se utiliza, el punto de ebullici??n del agua se marc?? a 73 y el punto de fusi??n del hielo a 51, de modo que el cero de su escala fue equivalente a aproximadamente -240 en la escala Celsius.

Esta notablemente aproximaci??n cercana al valor moderno de -273,15 ?? C para el cero del aire term??metro, se mejora a??n m??s por Johann Heinrich Lambert, quien le dio el valor de -270 ?? C y observ?? que esta temperatura puede ser considerado como el fr??o absoluto.

Los valores de este para que el cero absoluto no fueron, sin embargo, universalmente aceptadas sobre este per??odo. Pierre-Simon Laplace y Antoine Lavoisier , en su tratado sobre el calor 1780, llegaron a valores que van de 1500 a 3000 por debajo del punto de congelaci??n del agua, y pens?? que en cualquier caso debe ser de al menos 600 a continuaci??n. John Dalton en su Filosof??a Qu??mica dio diez c??lculo de este valor, y finalmente adopt?? -3000 ?? C como el cero natural de la temperatura.

Puesto que la temperatura es la medida de la energ??a cin??tica media en un sistema, es posible que algunas mol??culas de alcanzar un estado de no energ??a cin??tica mientras que otros tienen m??s energ??a cin??tica de la energ??a medida. Dado que el promedio entre las mediciones inferiores y superiores nos dan la temperatura leemos, es muy posible que algunas mol??culas para alcanzar cero Kelvin.

La obra de Lord Kelvin

Despu??s JP Joule hab??a determinado el equivalente mec??nico del calor, Lord Kelvin abord?? la cuesti??n desde un punto de vista totalmente diferente, y en 1848 ide?? una escala de temperatura absoluta que era independiente de las propiedades de cualquier sustancia en concreto y se basa ??nicamente en lo fundamental leyes de la termodin??mica. De ello se desprende de los principios sobre los que se construy?? esta escala que su cero se coloc?? en -273.150 ?? C, en casi exactamente el mismo punto que el cero del aire term??metro.

Informaci??n Adicional

Se puede demostrar a partir de las leyes de la termodin??mica que el cero absoluto nunca se puede lograr artificialmente, aunque es posible alcanzar temperaturas cerca de ella mediante el uso de Sistemas de refrigeraci??n criog??nicos. Este es el mismo principio que asegura que no se m??quina puede ser 100% eficiente.

A temperaturas muy bajas en las proximidades de cero absoluto, la materia exhibe muchas propiedades inusuales, incluyendo la superconductividad , superfluidez, y La condensaci??n de Bose-Einstein. Con el fin de estudiar tales fen??menos, los cient??ficos han trabajado para obtener temperaturas cada vez m??s bajas.

• En 1994, investigadores de la NIST alcanz?? una temperatura fr??a el entonces r??cord de 700 nK (mil millon??simas de kelvin).
• En noviembre de 2000 se registraron temperaturas de esp??n nuclear por debajo de 100 pK para un experimento en el Universidad de Helsinki de Baja Temperatura Laboratorio de Tecnolog??a. Sin embargo, esta fue la temperatura de un grado particular de la libertad de una propiedad cu??ntica llamada esp??n-no la temperatura termodin??mica promedio general nuclear para todos los posibles grados de libertad.
• En febrero de 2003, el Nebulosa Boomerang se encontr?? que era -272,15 ?? C; 1 K, el lugar m??s fr??o conocido fuera de un laboratorio. La nebulosa es 5.000 a??os luz de la Tierra y se encuentra en la constelaci??n Centaurus.

Termodin??mica cercanas al cero absoluto

A temperaturas cercanas a 0 K, movimiento casi todos molecular cesa y 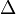S = 0 para cualquier proceso adiab??tico. Las sustancias puras pueden (idealmente) formar perfectos cristales como T 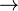0. Max Planck forma fuerte de la 's tercera ley de la termodin??mica establece la entrop??a de un cristal perfecto desvanece en el cero absoluto. Sin embargo, esto no puede ser cierto si el estado de menor energ??a es degenerado, o m??s de uno microestado. El original Teorema de Nernst calor hace que la demanda m??s d??bil y menos pol??mico que el cambio de entrop??a para cualquier proceso isot??rmico aproxima a cero cuando T 0

La implicaci??n es que la entrop??a de un cristal perfecto, simplemente se acerca a un valor constante.

El postulado de Nernst identifica el isoterma T = 0 como coincidente con el adiabat S = 0, aunque otras isotermas y adiab??ticas son distintos. Como no hay dos adiab??ticas se cruzan, hay otra adiab??tica puede intersectar el T = 0 isoterma. En consecuencia hay un proceso adiab??tico iniciado a temperatura distinta de cero puede llevar a la temperatura cero. (≈ Callen, pp. 189-190)

Una afirmaci??n a??n m??s fuerte es que es imposible por cualquier procedimiento para reducir la temperatura de un sistema a cero en un n??mero finito de operaciones. (≈ Guggenheim, p. 157)

Un cristal perfecto es aquel en el que el interno estructura de la red se extiende sin interrupci??n en todas las direcciones. El perfecto orden puede ser representado por traslaci??n simetr??a a lo largo de tres (no generalmente ortogonal) ejes . Cada elemento de entramado de la estructura est?? en su lugar apropiado, si se trata de un solo ??tomo o una agrupaci??n molecular. Para sustancias que tienen dos (o m??s) formas cristalinas estables, como el diamante y grafito de carbono , hay una especie de "degeneraci??n qu??mica". La pregunta sigue siendo si ambos pueden tener entrop??a cero a T = 0, aunque cada uno est?? perfectamente ordenado.

Cristales perfectos nunca ocurren en la pr??ctica; imperfecciones y materiales amorfos incluso enteras, simplemente son "congelados en" a bajas temperaturas, por lo que las transiciones a m??s no se produzcan estados estables.

Usando el Modelo de Debye, la el calor y la entrop??a de un cristal puro espec??fica son proporcionales a T ^3, mientras que la entalp??a y potencial qu??mico es proporcional a T ^4. (Guggenheim, p. 111) Estas cantidades caer hacia sus T = 0 valores l??mite y el enfoque con cero pistas. Para los calores espec??ficos, por lo menos, el valor l??mite en s?? es definitivamente cero, como se ve confirmada por los experimentos por debajo de 10 K. Incluso el menos detallado Einstein modelo muestra esta curiosa ca??da de los calores espec??ficos. De hecho, todos los calores espec??ficos se desvanecen en el cero absoluto, no s??lo los de los cristales. Asimismo para el coeficiente de expansi??n t??rmica. Las relaciones de Maxwell muestran que varias otras cantidades tambi??n se desvanecen. Estos fen??menos eran imprevisto.

Dado que la relaci??n entre los cambios en la energ??a de Gibbs , la entalp??a y la entrop??a es

As??, como T disminuye, Δ Δ G y H se aproximan entre s?? (siempre que est?? delimitada Δ S). Experimentalmente, se ha encontrado que todos los procesos espont??neos (incluyendo reacciones qu??micas ) resultan en una disminuci??n de G a medida que avanzan hacia equilbrium. Si Δ S y / o T son peque??as, la condici??n Δ G <0 puede implicar que Δ H <0, lo que indicar??a un reacci??n exot??rmica que libera calor. Sin embargo, esto no es necesario; reacciones endot??rmicas pueden proceder de forma espont??nea si el t??rmino T Δ S es lo suficientemente grande.

M??s que eso, las laderas de los derivados de temperatura de Δ G y Δ H convergen y son iguales a cero en T = 0, lo que asegura que Δ Δ G y H son casi los mismos en un intervalo considerable de las temperaturas, lo que justifica la aproximaci??n emp??rica Principio de Thomsen y Berthelot, que dice que el estado de equilibrio a la que un sistema procede es la que se desarrolla la mayor cantidad de calor, es decir, un proceso real es la m??s exot??rmica. (Callen, pp. 186-187)

Relaci??n con Bose Einstein Condensados

La Bose-Einstein es una sustancia que se comporta muy inusual pero s??lo a temperaturas extremadamente bajas, tal vez unas pocas millon??simas encima del cero absoluto. Es en este punto el leyes de la termodin??mica se vuelven muy importantes.

Escalas de temperatura absolutas

Absoluto o temperatura termodin??mica se mide convencionalmente en grados Kelvin ( Celsius -scaled incrementos), y cada vez m??s rara en el Escala Rankine ( Incrementos a escala Fahrenheit). Temperatura absoluta se determina de forma ??nica hasta una constante multiplicativa que especifica el tama??o del "grado", por lo que las proporciones de dos temperaturas absolutas, T ₂ / T _1, son los mismos en todas las escalas. La definici??n m??s transparente proviene de la cl??sica Distribuci??n sobre energ??as, o de los an??logos cu??nticos Maxwell-Boltzmann: Estad??stica de Fermi-Dirac (part??culas de medio entero spin) y Estad??stica de Bose-Einstein (part??culas de esp??n entero), todos los cuales dan el n??mero relativo de part??culas como (decreciente) funciones exponenciales de energ??a m??s kT. En un nivel macrosc??pico, una definici??n puede darse en t??rminos de la eficiencia de "reversible" motores de calor que opera entre dep??sitos t??rmicos m??s calientes y m??s fr??as.

Temperaturas negativas

Ciertos sistemas semi-aisladas, tales como un sistema de no interact??an gira en un campo magn??tico, puede alcanzar temperaturas negativas; sin embargo, no son en realidad m??s fr??o que el cero absoluto. Se pueden sin embargo considerarse como "m??s caliente que T = ∞", como energ??a fluir?? desde un sistema de temperatura negativo a cualquier otro sistema con la temperatura positivo al contacto.