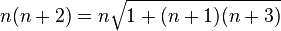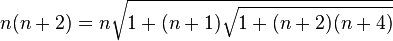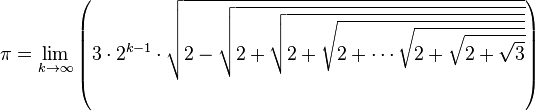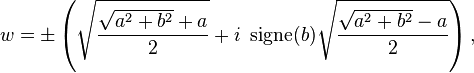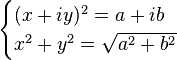Racine carrée
|
|
Cet article ne cite pas suffisamment ses sources (mars 2008). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » (modifier l'article, comment ajouter mes sources ?).
|

 se note
se note  .
.La racine carrée d’un nombre réel positif  est le nombre positif qui, lorsqu'il est multiplié par lui-même, donne
est le nombre positif qui, lorsqu'il est multiplié par lui-même, donne  , c'est-à-dire le nombre positif dont le carré vaut
, c'est-à-dire le nombre positif dont le carré vaut  . On le note
. On le note  ou
ou  ½ ; dans cette expression,
½ ; dans cette expression,  est appelé le radicande et le signe √ est appelé le radical.
est appelé le radicande et le signe √ est appelé le radical.
Une tablette d'argile datée du XVIIIe siècle av. J.-C. montre que les Babyloniens connaissaient la racine carrée de deux et un algorithme pour son calcul[1] [2].
Tout nombre réel x positif possède une racine carrée qui est elle-même un nombre réel. La racine carrée d'un nombre entier n est soit un entier, soit un nombre irrationnel, c'est-à-dire qu'elle ne peut être exprimée par une fraction. La racine carrée est à l'origine de la découverte de l’irrationalité, mais contrairement à une idée répandue, rien n'assure que celle de 2 fut le premier nombre irrationnel connu[3]. L'exemple de démonstrations par l'absurde choisi par Aristote, l'un des fondateurs de la logique, s'appuie sur l’irrationalité de 2 : « Ils prouvent que la diagonale du carré est incommensurable au côté en montrant que, si l'on admet qu'il lui est commensurable, un nombre impair serait égal à un pair[4]. »
À la Renaissance, des mathématiciens ont été amenés à définir la racine carrée d'un nombre négatif, ce qui a conduit à l'avènement des nombres complexes. L'extraction d'une racine carrée était la cinquième « opération classique ». Elle est aussi perçue comme une fonction.
Histoire

La plus ancienne racine carrée connue apparaît vers 1 700 av. J.-C. sur la tablette YBC 7289. Il s'agit de la représentation d'un carré avec, sur un côté, le nombre 30 et, le long de la diagonale, une valeur approchée de √2.
Construction géométrique de la racine carrée
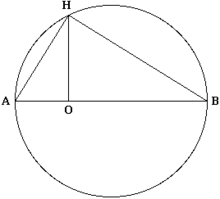
La construction géométrique suivante se réalise à la règle et au compas et permet, étant donné un segment OB de longueur a, et un segment de longueur 1, de construire un segment de longueur 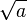 :
:
- Construire le segment [AB] de longueur 1+a et contenant le point O avec AO = 1
- Construire le cercle c de diamètre [AB].
- Construire la droite d perpendiculaire à (OB) et passant par O.
- Nommer H le point d’intersection du cercle c et de la droite d.
Le segment [OH] est de longueur 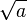 .
.
La preuve consiste à appliquer le théorème de Pythagore :
- Au triangle rectangle HOB : OH2 + a2 = HB2
- Au triangle rectangle ABH : HB2 = (a+1)2 - AH2
- Au triangle rectangle AOH : AH2 = 12 + OH2
D’où OH2 + a2 = (a+1)2 - (12 + OH2), soit, après simplification OH2 = a, et donc OH = 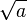 .
.
Cette construction a son importance dans l’étude des nombres constructibles.
Fonction réelle

L’application  est une bijection de ℝ+ sur ℝ+ dont la réciproque est notée
est une bijection de ℝ+ sur ℝ+ dont la réciproque est notée  . Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de l'un de ses côtés.
. Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de l'un de ses côtés.
Mise en garde : l’aire s’exprime dans le système universel en mètre carré et les longueurs en mètre. En prenant la racine carrée d’une quantité exprimée en mètres carrés, on obtient une quantité exprimée en mètres. Les physiciens attachent une importance particulière à l’analyse des unités ; cet aspect est effacé en mathématiques. Les nombres réels sont des constantes sans unité, et la racine carrée d’un nombre réel positif est un nombre réel positif.
La fonction racine carrée vérifie les propriétés élémentaires suivantes valables pour tous nombres réels positifs x et y :
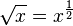

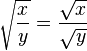 (sous la condition
(sous la condition 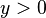 )
) .
.
- Elle est strictement croissante, comme réciproque d'une bijection croissante sur ℝ+.
- Elle est 1/2-höldérienne donc continue.
- Elle est dérivable en tout réel strictement positif
 , mais elle n’est pas dérivable en
, mais elle n’est pas dérivable en 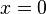 . En ce point, la courbe représentative admet une demi-tangente verticale. Sa fonction dérivée est donnée par :
. En ce point, la courbe représentative admet une demi-tangente verticale. Sa fonction dérivée est donnée par :
Notons f la fonction racine carrée.
- Si
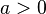 alors, pour tout
alors, pour tout  tel que
tel que 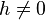 ,
,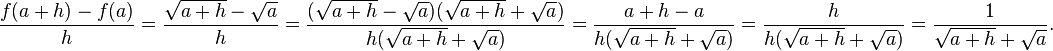
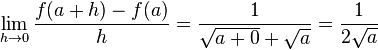 . La fonction est bien dérivable pour tout réel
. La fonction est bien dérivable pour tout réel 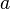 strictement positif.
strictement positif. - Si
 alors, pour tout
alors, pour tout  , on a
, on a
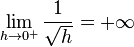 . Donc
. Donc 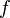 n'est pas dérivable en 0.
n'est pas dérivable en 0.
- Elle est de classe
 sur ℝ+* :
sur ℝ+* :
- Son développement en série de Taylor au point 1 est donc, pour tout réel h tel que |h| ≤ 1 :

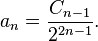

Extraction de racines carrées
Le calcul de la racine carré d'un nombre positif n'est pas toujours évident, notamment pour de grands nombres. Ainsi, plusieurs algorithmes ont été développés au cours de l'histoire afin d'obtenir ce nombre.
La méthode de Héron
La méthode de Héron est un algorithme permettant d’approcher les racines carrées. Elle a été développée par les Babyloniens, et fournit de bonnes approximations au prix de quelques divisions. Pour calculer une valeur approchée de la racine carrée d'un nombre a, on part d'une approximation grossière r de sa racine carrée et on affine l'approximation en ajoutant à r un terme correctif égal à  , de sorte que la nouvelle valeur approchée est
, de sorte que la nouvelle valeur approchée est 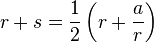 . Cette méthode peut être itérée, et est identique à la méthode de Newton appliquée à la résolution de l'équation
. Cette méthode peut être itérée, et est identique à la méthode de Newton appliquée à la résolution de l'équation  . La vitesse de convergence des approximations successives vers la valeur exacte est quadratique.
. La vitesse de convergence des approximations successives vers la valeur exacte est quadratique.
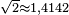
Prenons la valeur rapprochée  . On calcule de proche en proche :
. On calcule de proche en proche :
On a ainsi obtenu la racine carrée de 2 à la précision 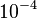 .
.
On trouve dans un manuscrit indien, dit manuscrit de Bakshali, datant peut-être du VIIe siècle, une correction différente de la méthode de Héron, la nouvelle valeur approchée étant  , sans qu'on sache comment cette approximation a été trouvée. Elle est équivalente à appliquer deux fois de suite la méthode de Héron[5]. L'itération de cette dernière méthode donne une vitesse de convergence bi-quadratique.
, sans qu'on sache comment cette approximation a été trouvée. Elle est équivalente à appliquer deux fois de suite la méthode de Héron[5]. L'itération de cette dernière méthode donne une vitesse de convergence bi-quadratique.
Approximation de √a à l'aide de suites adjacentes
Soit 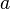 un nombre réel strictement positif.
un nombre réel strictement positif.
Considérons les suites u et v définies par :
-
 ,
, -
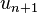 est la moyenne harmonique de
est la moyenne harmonique de 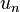 et
et  , soit
, soit 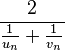 ,
, -
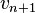 est la moyenne arithmétique de
est la moyenne arithmétique de 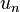 et
et  , soit
, soit .
.
Les suites  et
et  sont adjacentes, et convergent vers la même limite :
sont adjacentes, et convergent vers la même limite : 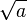 . L'erreur est majorée par la différence
. L'erreur est majorée par la différence 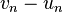 . La suite
. La suite  n'est autre que la suite obtenue en itérant la méthode de Héron à partir de la valeur 1.
n'est autre que la suite obtenue en itérant la méthode de Héron à partir de la valeur 1.
Remarquons l'originalité de cette présentation qui mêle moyennes harmonique, géométrique et arithmétique. En effet 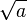 n'est autre que la moyenne géométrique de 1 et de a, et si on remplace
n'est autre que la moyenne géométrique de 1 et de a, et si on remplace 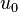 par un réel strictement positif quelconque b, les suites u et v convergent vers la moyenne géométrique
par un réel strictement positif quelconque b, les suites u et v convergent vers la moyenne géométrique  de a et b.
de a et b.
Un algorithme utilisant la notation décimale
L'introduction de la notation décimale des nombres par position a permis de développer un algorithme tirant parti de cette notation. On en trouve mention dans un ouvrage du mathématicien Indien Âryabhata, vers 499 après J.C.[6]. Il a été utilisé pendant plusieurs siècles et jusqu'au milieu du XXe siècle, avant l'invention des calculateurs électroniques. Âryabhata donne également un algorithme comparable permettant de calculer des racines cubiques.
On sépare les chiffres du nombre par paires en commençant à partir de la virgule. On place le nombre dont on veut extraire la racine en haut, de la même façon que lorsqu'on effectue une division selon la méthode classique ; la racine carrée sera inscrite au-dessus de ce nombre.
À chaque étape :
- on abaisse la paire de chiffres la plus significative non encore utilisée et on la place au côté d’un reste éventuel de l'étape précédente (initialement nul) ;
- soit r le résultat intermédiaire de la racine carrée obtenu précédemment (égal à zéro au début). On cherche le plus grand chiffre x tel que le nombre y=(20r + x)x ne dépasse pas le reste courant ;
- on complète r en plaçant la décimale x à sa droite, pour former le nouveau résultat intermédiaire ;
- on soustrait y de la valeur courante pour former le nouveau reste ;
- si le reste est nul et qu’il n’y a plus de chiffre à abaisser alors l’algorithme se termine sinon on recommence.
On remarque que la recherche de x en négligeant le terme en x2 n'est autre que la méthode de Héron.
(nota : la suite des chiffres en gras s'inscrit au fur et à mesure au-dessus du nombre initial, au-dessus de la paire de chiffre traité selon l'algorithme, et donne le résultat : 12,34. La place de la virgule est significative mais n'a pas besoin d'être prise en compte pendant les calculs, il suffit de la constater à la fin)
'''1 2 3 4'''
01 52,27 56 1 r=0 à cette étape
x=1 01 1 y=(20*0+1)1 = 1 <= 01 alors que (20*0+2)*2 = 4 > 01 donc x = 1
____ __ j'inscris le '''1''' : r=1 pour l'étape suivante
00 52 2x je pose 01-01=00 et j'abaisse 52 : apparait 52
x=2 00 44 12 y=(20*1+2)2 = 44 <= 52 alors que (20*1+3)*3= 69 > 52 donc x = 2
_______ __ j'inscris le '''2''' : r=12 pour l'étape suivante, 20*r = 240
08 27 24x 52-44 = 08, je pose 08 et j'abaisse 27 : apparait 827
x=3 07 29 123 y=(20*12+3)*3 = 243*3 = 729 < 827
_______ __ j'inscris le '''3''' : r=123 pour l'étape suivante, 20*r=2460
98 56 246x 827-729 = 98, je pose 98 et j'abaisse 56 : apparait 9856
x=4 98 56 1234 y=(20*123+4)*4 = 9856
_______ j'inscris le '''4''' : r=1234
00 -- 9856-9856 = 0 et il n'y a plus rien à abaisser : fin de l’algorithme
Jusqu’au XXe siècle on utilisait couramment cet algorithme en accélérant les calculs à l’aide d’un abaque formé d’un jeu de réglettes : les bâtons de Napier.
Bien que décrite ici pour des nombres écrits en base 10, la procédure fonctionne dans n’importe quelle base de numération, par exemple la base 2.
Une variante de cette méthode donne l'extraction de racine carrée par la méthode du goutte à goutte.
Méthode par les fractions continues
La fraction continue d'un irrationnel est la suite de ses approximations « optimales » par des fractions, c'est-à-dire que si p/q est une des valeurs de cette suite, alors aucune fraction de a/b avec b < q n'approche plus précisément le réel. Dans le cas particulier des racines carrées, on calcule relativement simplement cette suite, ainsi qu'une sous-suite qui correspond à un cas particulier de la méthode de Héron.
Méthode par dichotomie
On peut également procéder par dichotomie à condition de disposer d'un encadrement de la racine carrée cherchée. On peut pour cela utiliser le nombre de chiffres du nombre dont on cherche la racine carrée. Cette racine aurait moitié moins de chiffres. Ainsi, si le nombre possède 1 024 chiffres, sa racine carrée en possèdera entre 511 et 513. On peut également utiliser d'abord les méthodes précédentes pour obtenir une première valeur approchée de la racine carrée avant de procéder à la dichotomie.
L'algorithme de dichotomie est le suivant. Il évite de procéder à des divisions (autre que la division par 2 qui n'est qu'un décalage de registre si les nombres sont codés en binaire. Cette division est notée shr 1 ci-dessous).
function Racine_64(C: int64): int64;
var
A, B, D, D2: int64;
begin
A := borne basse;
B := borne haute;
repeat
D := (A + B) shr 1;
D2 := D * D; ⇐ on élève au carré avant de tester
if D2 > C then
A := D - 1
else
if C > D2 then
B := D + 1
else
Result := A;
until B > A;
end;
La même méthode s'applique pour les racines n-ièmes, en remplaçant le calcul de D2 = D*D par le calcul de D^n.
La méthode de dichotomie a cependant une vitesse de convergence plus lente que l'itération de la méthode de Héron.
Racines carrées particulières
Nombre d'or
L’identité 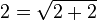 implique
implique  , et par itérations successives :
, et par itérations successives :
Pour des raisons analogues, on obtient :
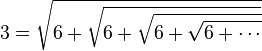
 ;…
;…
Si r est un entier strictement supérieur à 1,
Plus généralement, si p étant un nombre réel supérieur ou égal à 1,
Si p est égal à 1, on obtient le nombre d'or:
 .
.
Nombres entiers supérieurs à 1 sous forme de racines carrées
Le mathématicien Ramanujan obtint une formule alternative en partant de la décomposition
et construisit le produit  en fixant
en fixant 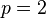
Il substitua le terme 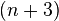
Ramanujan réitéra à l’infini en remplaçant maintenant 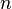 par 1 et obtint la jolie formule :
par 1 et obtint la jolie formule :
(bien entendu, il doit ensuite démontrer que le passage à la limite est légal ; il n'est pas difficile de montrer que la suite converge, mais le calcul de la limite est autrement plus délicat)
En fixant 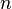 et
et 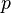 à d’autres valeurs positives ou en élevant au carré une formule obtenue, on peut également construire d’autres belles formules comme :
à d’autres valeurs positives ou en élevant au carré une formule obtenue, on peut également construire d’autres belles formules comme :
En résumé, la relation suivante, itérée à l’infini :
permet donc d’exprimer tous les nombres entiers strictement supérieurs à 1 comme une itération infinie de racines carrées.
En particulier, en fixant n = 0
(toutes ces formules sont en fait des affirmations sur des limites, qui se démontrent, de manière assez délicate, par encadrements)
Pi
Le nombre π s’exprime sous la forme d’une itération infinie de racines carrées :
 , où k est le nombre de racines carrées emboitées
, où k est le nombre de racines carrées emboitées
Ou encore :
(formules qui se démontrent par calcul trigonométrique direct : le terme de droite de la première, par exemple, vaut  ).
).
Notion algébrique générale
Soient x et a deux éléments d’un anneau A, tels que x2=a. L'élément x est alors une racine carrée de a. La notation √a est néanmoins souvent déconseillée car il peut exister plusieurs tels éléments x.
En général (si l'anneau n'est pas intègre ou s'il n'est pas commutatif), un élément peut avoir plus de deux racines carrées. Par exemple dans l'anneau Z/9Z, les racines carrées de 0 sont 0, 3 et -3, et dans le corps gauche des quaternions, tout réel strictement négatif possède une infinité de racines carrées.
Dans le cas des nombres réels, un auteur parlant d'une racine carrée de 2, traite d'un des deux éléments √2 ou bien −√2. En revanche l'expression la racine carrée de deux évoque toujours la solution positive. Comme l'expression √2 est toujours positive et le terme fonction racine définie sur les réels positifs désigne toujours la valeur positive, on évite cette confusion dans les enseignements un peu élémentaires des mathématiques en ne faisant usage que de l'expression : la racine carrée, alors toujours positive.
Racines carrées de nombres complexes
La racine carrée sur ℝ est définie seulement pour les nombres positifs. Dans la résolution effective des équations polynomiales, l’introduction d’une racine carrée formelle d’un nombre négatif dans les calculs intermédiaires donne des résultats exacts. C’est ainsi que le corps des nombres complexes a été introduit[7]
Pour tout nombre complexe non nul
(avec
et
réels), il existe exactement deux nombres complexes w tels que w2 = z. Ils sont opposés l'un de l'autre.
- Si b est non nul, ils sont données par :
avec
.
- Si b est nul et a est négatif, cette formule se simplifie en :
- Par ailleurs, si z n'est pas un réel négatif (i.e. si b est non nul ou si a est positif),
Pour trouver  tel que
tel que 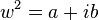 , on pose le système suivant :
, on pose le système suivant :
Par identification de la partie réelle et imaginaire, on obtient :
On en déduit alors 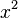 et
et 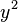 en ajoutant et soustrayant les première et troisième équations. Le signe du produit
en ajoutant et soustrayant les première et troisième équations. Le signe du produit 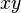 est celui de
est celui de 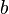 , d'où la première expression des deux couples de solutions pour
, d'où la première expression des deux couples de solutions pour  et
et 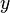 .
.
Mais une manière moins traditionnelle de résoudre ce système est de faire dans un premier temps seulement la somme (des première et troisième équations) :
ce qui, si z n'est pas un réel négatif, mène à la dernière formule.
Pour des raisons de nature topologique, il est impossible de prolonger la fonction racine carrée, de ℝ+ dans ℝ+, en une fonction continue  vérifiant
vérifiant  .
.
On appelle détermination de la racine carrée sur un ouvert U de ℂ toute fonction continue  vérifiant
vérifiant  .
.
La détermination principale de la racine carrée est la fonction de ℂ dans ℂ ainsi définie :
si z s’écrit sous forme trigonométrique  avec
avec 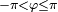 , alors on pose
, alors on pose  . Cette détermination principale n’est continue en aucun point de la demi-droite des réels strictement négatifs, et est holomorphe sur son complémentaire.
. Cette détermination principale n’est continue en aucun point de la demi-droite des réels strictement négatifs, et est holomorphe sur son complémentaire.
Quand le nombre est dans sa forme algébrique z=a+ib, cette définition se traduit par :
où le signe de la partie imaginaire de la racine est
- si
 : le signe de
: le signe de 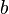
- si
 et
et  : le signe +
: le signe + - si
 et
et  : pas de signe (le nombre est nul).
: pas de signe (le nombre est nul).
Notons qu’à cause de la nature discontinue de la détermination principale de la racine carrée dans le plan complexe, la relation  devient fausse en général.
devient fausse en général.
Racines carrées de matrices et d’opérateurs
Si A est une matrice autoadjointe positive ou un opérateur autoadjoint positif en dimension finie, alors il existe exactement une matrice autoadjointe positive ou un opérateur autoadjoint positif B tel que B2 = A. On pose alors : √A = B.
Plus généralement, pour toute matrice normale ou tout opérateur normal en dimension finie A, il existe des opérateurs normaux B tels que B2 = A. Cette propriété se généralise à tout opérateur borné normal sur un espace de Hilbert.
En général, il y a plusieurs tels opérateurs B pour chaque A et la fonction racine carrée ne peut pas être définie pour les opérateurs normaux d’une façon satisfaisante (continue par exemple). Les opérateurs positifs sont apparentés à des nombres réels positifs, et les opérateurs normaux sont apparentés à des nombres complexes. Les articles sur la théorie des opérateurs développent davantage ces aspects.
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Square root » (voir la liste des auteurs).
- ↑ http://www.recreomath.qc.ca/dict_babyloniens_algorithme.htm
- ↑ http://it.stlawu.edu/~dmelvill/mesomath/tablets/YBC7289.html (en)
- ↑ Benoît Rittaud, Le Fabuleux destin de √2, SMF Gazette 107, janvier 2006.
- ↑ Aristote, Analytiques Postérieurs I, 23.
- ↑ T. Hayashi, The Bakhshali mauscript, an ancient Indian mathematical treatise, John Benjamins Publishing Company, Amsterdam (2005).
- ↑ W.E. Clarke, The Aryabhatiya of Aryabhata, an ancient Indian work on mathematics and astronomy, University of Chicago, Chicago IL (1930).
- ↑ Dans la résolution de l'équation du troisième degré, la méthode de Cardan s'applique formellement et donne des résultats réels, si l'on accepte d'introduire dans certains cas des racines carrées "imaginaires" de réels négatifs. Pour plus de détails, voir histoire des nombres complexes, et aussi la description des résultats de Bombelli.
Voir aussi
Articles connexes
- Équation du second degré
- Racine carrée de deux
- Racine carrée de trois
- Racine carrée de cinq
- Racine cubique
- Racine de nombre complexe
- Nombre d’or
- Nombre irrationnel
- Nombre algébrique
- Nombre réel
- Nombre complexe
- Exponentielle
- Résidu quadratique
Lien externe
(en) Suites concernant la racine carrée dans l'encyclopédie en ligne des suites de nombres entiers (entre autres : développements décimaux des racines carrées des entiers de 2 à 99)
Bibliographie
- (en) David Eugene Smith, History of Mathematics, vol. 2
- (en) George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, 2e éd., Penguin Books, London, 2000 (ISBN 0-691-00659-8)
- Portail des mathématiques
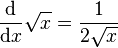

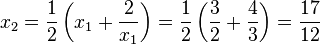



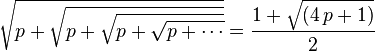
![(n+p)^2 = 1 + [n+(p-1)][n+(p+1)]\,](../i/m/d2b6141735aa5e63c004c2334fdd055e.png)