Opérateur (mathématiques)
|
|
Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques et en physique théorique, un opérateur est une application entre deux espaces vectoriels topologiques.
Définition d'un opérateur
Définition
Soient E et F deux espaces vectoriels topologiques. Un opérateur O est une application de E dans F :
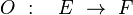 |
Opérateur linéaire
Par définition de la linéarité :
Un opérateur 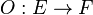 est linéaire si et seulement si :
est linéaire si et seulement si :
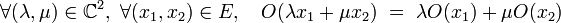 |
où 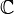 est le corps des scalaires de E et F.
est le corps des scalaires de E et F.
Remarque
Lorsque 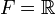 , un opérateur est une forme linéaire sur E.
, un opérateur est une forme linéaire sur E.
Domaine (de définition)
On étend la définition précédente à des applications linéaires définies seulement sur un sous-espace vectoriel de E, qu'on appelle alors domaine de définition de l'opérateur.
Continuité
Par définition de la continuité :
- Soient O un opérateur de domaine
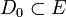 et à valeurs dans F, et
et à valeurs dans F, et 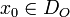 . L'opérateur O est dit continu en
. L'opérateur O est dit continu en 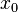 si et seulement si pour tout voisinage V de
si et seulement si pour tout voisinage V de  , il existe un voisinage
, il existe un voisinage 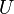 de
de 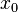 tel que :
tel que :
 |
- L'opérateur O est dit continu si et seulement s'il est continu en tous les points
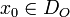 de son domaine.
de son domaine.
Articles connexes
- Opérateur différentiel
- Espace de Banach
- Espace de Hilbert
- Théorie ergodique
- Mécanique quantique
- Théorie quantique des champs axiomatique
Bibliographie
- A. N. Kolmogorov & S. V. Fomin ; Introductory Real Analysis, Dover Publications, Inc. (1975), ISBN 0-486-61226-0.
- T. Kato ; Perturbation Theory for Linear Operator, Serie : Classics in Mathematics, Springer-Verlag (2e édition-1995), ISBN 3-540-58661-X.
- B. Yosida ; Functionnal Analysis, Serie : Classics in Mathematics, Springer-Verlag (6e édition-1995), ISBN 3-540-58654-7.
- Portail des mathématiques
- Portail de la physique
