Papyrus Rhind

Un extrait du papyrus Rhind.

Détail de la première moitié du papyrus Rhind, original 199,5 × 32 cm, British Museum, EA 10058.

Le papyrus Rhind est un célèbre papyrus de la deuxième période intermédiaire qui a été écrit par le scribe Ahmès. Son nom vient de l'Écossais Alexander Henry Rhind qui l'acheta en 1858 à Louxor, mais il aurait été découvert sur le site de la ville de Thèbes. Depuis 1865 il est conservé au British Museum (à Londres). Avec le papyrus de Moscou, il est une des sources les plus importantes concernant les mathématiques dans l'Égypte antique.

Ahmès indique que son papyrus est, en partie, une copie de résultats plus anciens remontant au Moyen Empire (vers -2000). Le papyrus Rhind contient 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage, sur plus de cinq mètres de longueur et trente-deux centimètres de large. Il est rédigé en écriture hiératique.

Le papyrus

Description

Le papyrus Rhind se présentait à l'origine comme un rouleau constitué de quatorze feuilles soigneusement assemblées^[1]. Il est actuellement séparé en deux bandes de 32 cm de hauteur, la première de 199,5 cm de long (BM 10058) et la seconde de 295,5 cm de long (BM 10057) toutes deux conservées au British Museum qui les a acquises en 1865, auprès de l'exécuteur testamentaire de A. H. Rhind. Ces bandes étaient à l'origine solidaires et reliées par un morceau manquant de 18 cm. Des fragments de ce dernier ont été identifiés aux États-Unis en 1922 par Percy Edward Newberry, ils se trouvent aujourd'hui au Brooklyn Museum à New York^[2]. Malgré quelques lacunes, le papyrus est quasiment complet^[1]. Il se déroule en une succession de pages de la droite vers la gauche, écrites en hiératique (également de la droite vers la gauche). Le recto du papyrus est presque entièrement utilisé, avec quelques parties intermédiaires laissées vierges. Le verso est utilisé sur la première section (BM 10058), mais ne l'est pas sur la seconde section (BM 10057), en dehors de quelques inscriptions ajoutées vraisemblablement après la composition originelle^[3].

Découverte

Selon l'édition du fac-similé du papyrus publiée en 1898 par le British Museum, celui-ci a été découvert près du Ramesséum sur le site de Thèbes. Les deux principales sections, probablement découpées par les pilleurs, ont été achetées en 1858 par Rhind (à Louxor), les fragments de la petite partie intermédiaire en 1862 ou 1863 par le collectionneur américain Edwin Smith^[2].

Origine et datations

Le texte signé par le scribe Ahmès est daté par celui-ci de l'an 33 du règne du pharaon Apophis, souverain Hyksôs de la XV^e dynastie, qui règne en Basse-Égypte à Avaris dans la première moitié du XVI^e siècle avant notre ère, à la fin de la Deuxième Période intermédiaire^[4]. Ahmès annonce en introduction que le texte est une copie d'une version précédente datant d'un pharaon dont une partie du nom est effacée, mais qui parait être Amenemhat III, pharaon de la XII^e dynastie qui vivait près de trois siècles auparavant, à l'époque du Moyen Empire^[5], époque dont datent les autres papyrus mathématiques hiératiques qui nous sont parvenus^[6].

Le papyrus porte au verso, dans la partie centrale, de brèves inscriptions manifestement ajoutées après la composition, et datées de la onzième année du règne d'un pharaon inconnu^[7]. Elles font référence aux événements ayant conduit à la chute d'Avaris (celle-ci même n'est pas mentionnée) qui marque la fin des souverains Hyksôs chassés d'Égypte par le souverain de Thèbes (et futur pharaon de l'Égypte réunifiée) Ahmôsis. Leur interprétation est objet de débats^[8]. Si ces inscriptions ont été ajoutées avant le transfert du papyrus à Thèbes, la date pourrait renvoyer au règne de Khamoudy dernier roi Hyksôs de Basse-Égypte. Le papyrus aurait alors pu être ramené d'Avaris à Thèbes par l'armée victorieuse d'Ahmôsis, ce qui explique alors la découverte dans la capitale de la Haute-Égypte d'un papyrus originaire de Basse-Égypte^[9].

Usage

Tant la taille que le soin apporté à la composition et le peu d'erreurs relevées dans le texte témoignent de la qualité du document, qui est probablement un manuel de référence de haut niveau utilisé pour enseigner dans une école de scribes^[1],[10]. En cela il est très différent du papyrus de Moscou, la second source en importance pour les mathématiques égyptiennes du Moyen-Empire, plus ancien mais qui ressemble plutôt à une copie d'étudiant d'un manuel comparable au papyrus Rhind^[1].

Algorithmes de multiplication et division (problèmes 1 à 23)

Ces problèmes permettent de comprendre les techniques de multiplication et de division chez les Égyptiens.

Résolution d'équations par la méthode de fausse position (problèmes 24 à 34)

Voir Résolutions d'équations.

Les problèmes d'arpentage (problèmes 41 à 60)

L'arpentage, mesures des distances et les problèmes géométriques qui lui sont liés sont également abordés : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides.

Les problèmes 56, 57, 58, 59 et 60, sont consacrées à des calculs relatifs à la pente d'une pyramide, mesurée par leur sḳd ou seked, qui correspond à la demi base de la pyramide divisée par sa hauteur, autrement dit il s'agit de la cotangente de l'angle que forme la ligne de plus grande pente d'une face avec l'horizontale. Le seked est mesurée par le déplacement horizontal nécessaire pour rejoindre la face après une élévation verticale d'une coudée^[11], il s'exprime donc avec les unités de longueur en usage, coudée, paume, le septième d'une coudée, et doigt qui vaut le quart d'une paume. Pour quatre de ces problèmes le seked est de 5 paumes et 1 doigt. La cotangente est donc de (1/7) × (5+1/4) = 3/4 (ce qui correspond à une pente de 4/3)^[12].

Le triangle rectangle correspondant à cette pente, de côtés de l'angle droit proportionnels à 3 et 4, est donc un triangle 3-4-5. Cependant le papyrus Rhind ne traite que de la pente, et de fait le triangle 3-4-5 n'y est jamais mentionné^[13]. Cette inclinaison a été clairement choisie pour certaines pyramides de la VI^e dynastie, dont la base a pour côté 150 coudées et la hauteur 100 coudées. Sans que ce soit aussi manifestement intentionnel, celle de la pyramide de Khéphren en est proche^[14]. Il est tout à fait possible que le triangle et ses proportions aient été remarqués ; celles-ci facilitent la réalisation d'équerres triangulaires en bois qui auraient pu être utilisées pour vérifier la pente, mais cela reste hypothétique^[15].

Le disque de diamètre 9 a une aire voisine du carré de côté 8

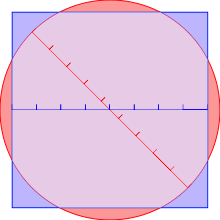
Dans les problèmes 48 et 50, Ahmes étudie le rapport liant l'aire d'un disque à son diamètre en cherchant à ramener l'aire de la circonférence à celle d'un carré équivalent : le papyrus Rhind précise en effet une première approche de la quadrature du cercle (construction d'un carré de même aire qu'un disque donné) : c'est le carré de côté 8d/9 où d est le diamètre du disque.

En d'autres termes, l'aire d'un disque de diamètre 9 unités est sensiblement égal à l'aire d'un carré de 8 unités de côté. Cette approximation^[16] se traduirait dans nos notations actuelles pour la surface d’un disque et d’un carré par :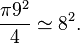

Cette approximation par la quadrature du cercle permit donc aux égyptiens de se passer de la constante π.

Notes et références

Bibliographie

• August Eisenlohr, Ein mathematisches Handbuch der alten Ägypter (Papyrus Rhind des British Museum), übersetzt und erklärt, Leipzig, 1877 - 1. Bd, Commentar (en ligne) ; 2. Bd, Tafeln ; 2^e éd. 1891 ; rééd. Wiesbaden, 1972 ;
• (en) T. Eric Peet, The Rhind Mathematical Papyrus : British Museum 10057 and 10058, London, Hodder & Stoughton for Liverpool University Press,‎ 1923 (éd. moderne des Papyrus Rhind) ;
• Arnold Buffum Chace, The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations, vol. II, 1927-1929.
• R. Gillings, Mathematics in the Time of the Pharaohs, Boston, MA: MIT Press, p. 202-205, 1972. (ISBN 0-262-07045-6) ;
• Gay Robins, Charles Shute, The Rhind Mathematical Papyrus, pages 41-43, British Museum, Dover reprint, 1987, (ISBN 0-486-26407-6) ;
• Sylvia Couchoud, Mathématiques Égyptiennes. Recherches sur les connaissances mathématiques de l’Égypte pharaonique, éditions Le Léopard d’Or,‎ 1993 (ISBN 2-86377-118-3) ;
• Michel Guillemot, Calcul et géométrie dans l’Égypte ancienne, dans Histoire du calcul de la géométrie à l'algèbre, dir. Luc Sinègre, Paris, 2009 (ISBN 978-2-7117-2226-6) (en ligne).
• Annette Imhausen, Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Harrassowitz, Wiesbaden 2003, (ISBN 3-447-04644-9)
• (en) Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press,‎ 2007 (1^re éd. 2003) (ISBN 978-0-521-69053-9)
• (en) Marshall Clagett, Ancient Egyptian Science, A Source Book. Volume Three: Ancient Egyptian Mathematics, American Philosophical Society, coll. « Memoirs of the American Philosophical Society »,‎ 1999 (ISBN 978-0-87169-232-0)
• (en) Anthony Spalinger, « The Rhind Mathematical Papyrus as a Historical Document », Studien zur Altägyptischen Kultur, Helmut Buske Verlag GmbH, vol. 17,‎ 1990, p. 295-337
• (en) Annette Imhausen (de), « Egyptian Mathematics », dans Victor J. Katz, The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton, Princeton University Press,‎ 2007 (ISBN 0-691-11485-4), p. 7-56

Voir aussi

Articles connexes

• Papyrus de Moscou
• Papyri d'El-Lahoun
• Papyrus de Berlin
• Rouleau de cuir des mathématiques égyptiennes (en)
• Tablettes de bois du Caire (en)

Liens externes

• (en) Le papyrus Rhind, sur le site du British Museum.
• (en) « Collections: Egyptian, Classical, Ancient Near Eastern Art: Fragments of Rhind Mathematical Papyrus », Brooklyn Museum (consulté le 25 novembre 2013)

• Portail de l’Égypte antique
• Portail de l’archéologie
• Portail des mathématiques
• Portail de Londres