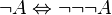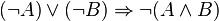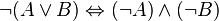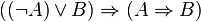Logique intuitionniste
L'intuitionnisme est une position philosophique vis-à-vis des mathématiques proposée par le mathématicien hollandais Luitzen Egbertus Jan Brouwer comme une alternative à l'approche dite classique. Elle a été ensuite formalisée, sous le nom de logique intuitionniste, par ses élèves V. Glivenko et Arend Heyting. Kurt Gödel a montré que l'on pouvait représenter la logique classique dans la logique intuitionniste et ceci bien que l'ensemble des formules valides de la logique intuitionniste soit strictement inclus dans l'ensemble des formules valides de la logique classique. Gerhard Gentzen en a formulé les règles de déduction dans le cadre de la déduction naturelle.
Les travaux récents, notamment la correspondance de Curry-Howard, lui ont donné un statut central dans la logique et dans l'informatique, en faisant d'elle historiquement la première des logiques constructives. Des travaux la concernant, effectués par Gödel et Andreï Kolmogorov au sujet de la « non-non interprétation » (interprétation de la double négation) ont ouvert la porte de l’interprétation de la logique classique dans les termes de la logique intuitionniste. L'étude de la logique intuitionniste est la clé pour bien comprendre la logique classique et ses subtilités.
Approche informelle
Brouwer a fondé l'intuitionnisme comme une position philosophique vis-à-vis des mathématiques ; cela l'a conduit à rejeter certaines formes du raisonnement mathématique traditionnel, qu'il jugeait contre-intuitives. En fait, il refusait deux principes.
- Le tiers exclu, qui consiste à dire qu'étant donnée une proposition
 , soit on a
, soit on a  , soit on a
, soit on a 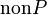 , formellement
, formellement 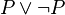 . À titre d'exemple, il rejetait le raisonnement suivant[1],[2] :
. À titre d'exemple, il rejetait le raisonnement suivant[1],[2] :
« Il existe des nombres irrationnels 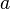 et
et 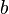 , tels que
, tels que 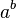 est un nombre rationnel. En effet, on sait que la racine carrée de deux est irrationnelle, et 2 est évidemment rationnel. En notant
est un nombre rationnel. En effet, on sait que la racine carrée de deux est irrationnelle, et 2 est évidemment rationnel. En notant 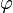 la proposition «
la proposition « 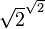 est rationnel », on pourrait alors dire :
est rationnel », on pourrait alors dire :
- si
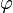 est vrai alors les irrationnels
est vrai alors les irrationnels 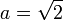 et
et 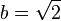 conviennent,
conviennent, - si
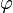 est faux alors les irrationnels
est faux alors les irrationnels 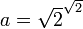 et
et 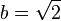 conviennent (l'irrationalité de
conviennent (l'irrationalité de 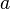 étant l’hypothèse
étant l’hypothèse  ), puisque
), puisque 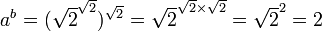 est rationnel ».
est rationnel ».
La critique de cette démonstration est qu'elle n'est pas constructive : de par son utilisation du tiers exclu, elle n'exhibe pas une solution explicite, mais démontre seulement l'existence d'un couple-solution sans pouvoir préciser lequel (puisqu'on ne sait pas si 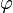 est vrai ou faux). En fait, le théorème de Gelfond-Schneider permet de montrer que
est vrai ou faux). En fait, le théorème de Gelfond-Schneider permet de montrer que 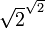 est transcendant, donc irrationnel, et que c'est donc
est transcendant, donc irrationnel, et que c'est donc 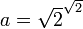 qu'il faut choisir, mais la démonstration fondée sur le tiers exclu ne le dit pas.
qu'il faut choisir, mais la démonstration fondée sur le tiers exclu ne le dit pas.
- L'existentiel non constructif. Brouwer veut que quand un mathématicien affirme il existe
 tel que
tel que  est
est  , que l'on écrirait formellement
, que l'on écrirait formellement 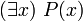 , il donne aussi un moyen de construire
, il donne aussi un moyen de construire  qui satisfait
qui satisfait  .
.
Brouwer a prôné une mathématique qui rejetterait le tiers exclu et n'accepterait que l'existentiel constructif. Cette attitude a été assez violemment critiquée par des mathématiciens comme David Hilbert tandis que d'autres comme Hermann Weyl y ont souscrit. Une fois formalisée, trois faits font de la logique intuitionniste une logique à part entière : l'existence de modèles qui en font un système complet de déduction, la découverte de son contenu calculatoire, connu sous le nom de correspondance de Curry-Howard, enfin le fait qu'elle est une logique modale. La logique intuitionniste n'a donc rien d'exotique. Allant plus loin, le logicien Jean-Yves Girard a proposé une logique plus faible que la logique intuitionniste, qu'il a appelée la logique linéaire, qui se trouve à la base de toute logique et qui permet de mieux comprendre la logique intuitionniste en particulier.
La logique intuitionniste revisite aussi le concept d'implication. L'implication 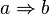 n'est plus l'implication matérielle
n'est plus l'implication matérielle 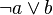 . Quand un mathématicien intuitionniste affirme
. Quand un mathématicien intuitionniste affirme 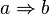 , il veut dire qu'il fournit un procédé de « construction » d'une démonstration de
, il veut dire qu'il fournit un procédé de « construction » d'une démonstration de 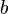 à partir d'une démonstration de
à partir d'une démonstration de 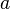 . Ceci est d'ailleurs la clé du contenu calculatoire de la logique intuitionniste.
. Ceci est d'ailleurs la clé du contenu calculatoire de la logique intuitionniste.
Approche formelle
Nous venons de voir que l'implication et la disjonction ne sont plus liées. Mais en fait cela va plus loin : une des caractéristiques de la logique intuitionniste est le fait que chaque connecteur 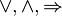 , l’absurde ⊥ et chaque quantificateur
, l’absurde ⊥ et chaque quantificateur 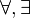 , doit être défini à partir de ses propres règles, autrement dit il n'y a pas de moyen de ramener la logique à un connecteur et à un quantificateur. C'est pourquoi nous allons donner des règles pour chaque connecteur ainsi que pour l’absurde.
, doit être défini à partir de ses propres règles, autrement dit il n'y a pas de moyen de ramener la logique à un connecteur et à un quantificateur. C'est pourquoi nous allons donner des règles pour chaque connecteur ainsi que pour l’absurde.
La logique implicative minimale
Pour introduire la logique intuitionniste, le plus simple est de commencer par la déduction naturelle en logique implicative minimale, qui est la logique propositionnelle dans laquelle il n'y a qu'un connecteur, l'implication 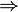 .
.
En déduction naturelle, 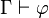 se lit « de l'ensemble de propositions
se lit « de l'ensemble de propositions 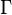 on déduit la proposition
on déduit la proposition 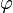 ».
».
Il y a alors deux règles (voir plus bas Lecture des règles) :
 .
.La première règle s'appelle la règle d'élimination de l'implication, tandis que la seconde règle s'appelle la règle d'introduction de l'implication. On remarque que l'élimination de l'implication est aussi le modus ponens bien connu. La méthode qui consiste à avoir pour chaque connecteur une (ou des) règle(s) d'élimination et une (ou des) règle(s) d'introduction est typique de la déduction naturelle et nous allons la retrouver par la suite.
Ce système de déduction est très simple (rasoir d'Ockham), mais il est moins puissant que la logique classique, car on ne peut y démontrer la loi de Peirce 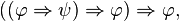 ni la proposition
ni la proposition 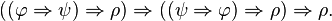
Lecture des règles
La règle d'élimination de l'implication peut se lire comme suit : si de l'ensemble d'hypothèses 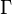 je déduis
je déduis  et si de plus de l'ensemble d'hypothèses
et si de plus de l'ensemble d'hypothèses 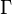 je déduis
je déduis 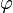 alors de l'ensemble d'hypothèses
alors de l'ensemble d'hypothèses 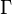 je déduis
je déduis 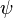 . Nous verrons (section interprétation de la logique intuitionniste) que l'expression « je déduis » prend un sens plus fort en logique intuitionniste qu'en logique classique. La règle d'introduction de l'implication, quant à elle, peut se lire comme suit : si de l'ensemble d'hypothèses
. Nous verrons (section interprétation de la logique intuitionniste) que l'expression « je déduis » prend un sens plus fort en logique intuitionniste qu'en logique classique. La règle d'introduction de l'implication, quant à elle, peut se lire comme suit : si de l'ensemble d'hypothèses 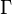 et de l'hypothèse
et de l'hypothèse 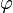 je déduis
je déduis 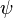 alors de l'ensemble d'hypothèses
alors de l'ensemble d'hypothèses 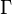 je déduis
je déduis  .
.
La logique propositionnelle intuitionniste
On conserve les règles de la logique implicative minimale concernant l'implication.
Ex falso quodlibet
En logique intuitionniste, comme en logique classique, est acceptée la règle suivante :
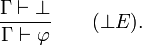
Cette règle est nommée principe d'explosion, ou en latin, ex falso quodlibet. ⊥ est la notation de L'absurde, c'est-à-dire d'une proposition fausse pour toutes les interprétations. Le principe d'explosion signifie que si un ensemble de propositions Γ conduit à l'absurde, alors de cet ensemble de propositions Γ, je peux déduire n'importe quelle proposition 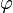 .
.
La négation
Traditionnellement, on considère la négation comme une abréviation. Plus précisément on dit que 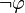 est en fait une abréviation pour
est en fait une abréviation pour 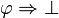 . Il n'y a donc pas de règles spécifiques à la négation.
. Il n'y a donc pas de règles spécifiques à la négation.
La conjonction
On introduit un nouveau connecteur binaire 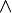 , représentant la conjonction de deux formules. On lit
, représentant la conjonction de deux formules. On lit 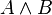 : A et B. On lui associe deux règles d'élimination,
: A et B. On lui associe deux règles d'élimination, 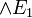 et
et 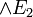 , et une règle d'introduction.
, et une règle d'introduction.
 .
.La disjonction
On introduit un nouveau connecteur binaire 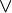 , représentant la disjonction de deux formules. Il est en quelque sorte symétrique du connecteur
, représentant la disjonction de deux formules. Il est en quelque sorte symétrique du connecteur 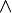 . Ainsi, on lui associe une règle d'élimination et deux règles d'introduction.
. Ainsi, on lui associe une règle d'élimination et deux règles d'introduction.
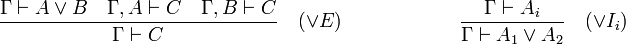 .
.On remarque que la règle d'élimination de la disjonction est une règle tryadique, c'est-à-dire qu'elle a trois prémisses.
Le calcul des prédicats intuitionniste
Le calcul des prédicats intuitionniste reprend toutes les règles du calcul propositionnel intuitionniste ci-dessus et lui adjoint de nouvelles règles pour les quantificateurs « quel que soit » et « il existe ». Son langage et son ensemble de formules demeurent les mêmes que ceux du calcul des prédicats classiques.
Remarque : Nous rappelons que A[t/x] signifie le remplacement de toutes les occurrences librement substituables de la variable x par le terme t ; voir calcul des prédicats pour les notions de « variable », « terme », « substitution » et de « librement substituable ».
Le quantificateur universel
- Règle d'introduction :
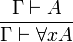
- Règle d'élimination :
![\frac{\Gamma , A[t/x] \vdash B}{\Gamma, \forall x A\vdash B}](../i/m/b12173219b765cc49681448b4cb3b857.png)
Le quantificateur existentiel
- Règle d'introduction :
![\frac{\Gamma \vdash A[t/x]}{\Gamma \vdash \exists x A}](../i/m/2edc6baa31d72d6422772b0bff16119a.png)
- Règle d'élimination :
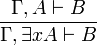
Exemples de différences avec la logique classique
Les opérations ne sont pas définies l’une par rapport à l’autre (voir plus loin), et ne sont définies qu’en elles-mêmes. Elles sont définies par l’interprétation qui doit en être faite. Pour cette raison, en plus des règles de calcul, sont données les interprétations qui doivent être faites des expressions de chaque opérateur[3].
Négation
On peut interpréter 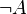 comme : « Il est démontré que
comme : « Il est démontré que  est contradictoire ».
est contradictoire ».
On dispose en logique intuitionniste du théorème suivant :
Mais on ne peut pas en conclure que 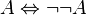 est vrai. En effet, cette dernière équivalence ne peut être prouvée en logique intuitionniste.
est vrai. En effet, cette dernière équivalence ne peut être prouvée en logique intuitionniste.
Double négation
On peut interpréter 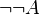 comme : « Il est prouvé qu’il est contradictoire d’affirmer que
comme : « Il est prouvé qu’il est contradictoire d’affirmer que  est contradictoire », c'est-à-dire « Il est prouvé que
est contradictoire », c'est-à-dire « Il est prouvé que  n’est pas contradictoire ». Mais on ne peut pas en déduire que «
n’est pas contradictoire ». Mais on ne peut pas en déduire que «  est vrai ».
est vrai ».
On dispose en logique intuitionniste du théorème suivant :
Mais la réciproque n’est pas vraie. On n'a pas 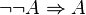 . L’expression
. L’expression 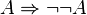 peut s’interpréter comme « Si
peut s’interpréter comme « Si  est vraie, alors
est vraie, alors  n’est pas contradictoire ». Mais le fait que
n’est pas contradictoire ». Mais le fait que  ne soit pas contradictoire n’est pas suffisant pour établir une preuve que «
ne soit pas contradictoire n’est pas suffisant pour établir une preuve que «  est vraie ».
est vraie ».
À titre d'exemple, soit x un réel et  la proposition x est rationnel. Prouver
la proposition x est rationnel. Prouver  , c'est donner deux entiers a et b tels que x = a/b. Si
, c'est donner deux entiers a et b tels que x = a/b. Si  est contradictoire (et donc si on a
est contradictoire (et donc si on a 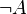 ), c'est que x est non rationnel, ou irrationnel. Dire que l'on a
), c'est que x est non rationnel, ou irrationnel. Dire que l'on a 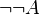 , c'est dire que supposer x irrationnel conduit à une contradiction, et donc conclure que x n'est pas irrationnel. Mais ce n'est pas suffisant pour établir l'existence effective de deux entiers a et b tels que x = a/b. Ainsi, en logique intuitionniste, ne pas être irrationnel est une propriété différente et plus faible que celle d'être rationnel.
, c'est dire que supposer x irrationnel conduit à une contradiction, et donc conclure que x n'est pas irrationnel. Mais ce n'est pas suffisant pour établir l'existence effective de deux entiers a et b tels que x = a/b. Ainsi, en logique intuitionniste, ne pas être irrationnel est une propriété différente et plus faible que celle d'être rationnel.
Conjonction
L'interprétation de 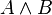 est : on dispose d'une preuve de
est : on dispose d'une preuve de  et d'une preuve de
et d'une preuve de 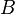 (comparable à ce qu’il en est en logique classique).
(comparable à ce qu’il en est en logique classique).
En logique intuitionniste, la proposition suivante est un théorème :
Mais contrairement à ce qu’il en serait en logique classique, 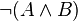 n’est seulement qu’une conséquence de
n’est seulement qu’une conséquence de 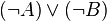 , la réciproque étant fausse. En effet, supposer que
, la réciproque étant fausse. En effet, supposer que 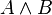 est contradictoire, est insuffisant en logique intuitionniste pour conclure si
est contradictoire, est insuffisant en logique intuitionniste pour conclure si  seul l'est ou
seul l'est ou 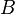 seul ou s'ils le sont tous les deux. Par exemple, supposer qu'un nombre est à la fois rationnel et irrationnel est contradictoire, mais insuffisant pour conclure si ce nombre est irrationnel ou non.
seul ou s'ils le sont tous les deux. Par exemple, supposer qu'un nombre est à la fois rationnel et irrationnel est contradictoire, mais insuffisant pour conclure si ce nombre est irrationnel ou non.
Disjonction
L'interprétation de 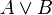 est : on a une preuve de
est : on a une preuve de  ou une preuve de
ou une preuve de 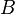 .
.
On dispose en logique intuitionniste du théorème suivant :
A et B s’excluent mutuellement et ne sont pas simultanément vrais. Cette situation est comparable à ce qu’il en serait dans la logique classique de Boole et Karnaugh.
Par contre, le théorème suivant :
est valide en logique intuitionniste, mais pas sa réciproque. En effet, si x est un nombre réel, on sait que s'il est rationnel alors il n'est pas irrationnel, mais on n'est pas pour autant capable de conclure si ce nombre est irrationnel ou non.
Quantificateur existentiel
L'interprétation de 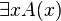 est : nous pouvons créer un objet
est : nous pouvons créer un objet  et prouver que
et prouver que 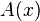 . L'existence de x est ici effective ou constructive. Il ne s'agit pas d'une existence théorique d'un élément
. L'existence de x est ici effective ou constructive. Il ne s'agit pas d'une existence théorique d'un élément  vérifiant
vérifiant 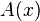 .
.
On dispose du théorème suivant :
S’il n’existe pas de x qui vérifie A(x) alors pour tous les x on ne vérifie pas A(x), d’où l’équivalence (qui correspond à l’intuition et se formule naturellement). Cette propriété est comparable à ce qu’il en serait en logique classique.
Quantificateur universel
L'interprétation de 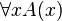 est : on a une preuve que pour chaque x appartenant à l’ensemble spécifié, on peut prouver A(x) (comparable à ce qu’il en est en logique classique).
est : on a une preuve que pour chaque x appartenant à l’ensemble spécifié, on peut prouver A(x) (comparable à ce qu’il en est en logique classique).
On dispose en logique intuitionniste du théorème suivant :
Mais contrairement à ce qu’il en serait en logique classique, la réciproque est fausse. En effet, cette réciproque exigerait que, en supposant contradictoire l'universalité de la propriété 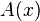 , on soit capable d'exhiber explicitement un objet x invalidant
, on soit capable d'exhiber explicitement un objet x invalidant 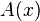 , ce qui n'est rarement possible.
, ce qui n'est rarement possible.
On peut aussi dire que, en logique intuitionniste, l'affirmation de 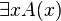 est l'affirmation de l'existence effective et constructible d'un objet x validant
est l'affirmation de l'existence effective et constructible d'un objet x validant 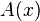 , alors que
, alors que 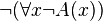 n'en est que l'existence théorique, exprimant seulement qu'il est contradictoire que
n'en est que l'existence théorique, exprimant seulement qu'il est contradictoire que 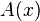 soit universellement contradictoire. La logique classique ne fait aucune distinction entre ces deux existences, alors que la logique intuitionniste considère la deuxième comme plus faible que la première.
soit universellement contradictoire. La logique classique ne fait aucune distinction entre ces deux existences, alors que la logique intuitionniste considère la deuxième comme plus faible que la première.
Tiers exclu
La proposition suivante
est un théorème de la logique classique, mais pas de la logique intuitionniste. Dans cette dernière, elle signifierait que nous pouvons prouver  ou prouver
ou prouver 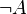 , ce qui n'est pas toujours possible.
, ce qui n'est pas toujours possible.
Par exemple, en arithmétique munie de la logique intuitionniste (dite arithmétique de Heyting), l’expression 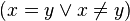 est valide, car pour tout couple d'entiers, on peut prouver qu'ils sont égaux, ou on peut prouver qu'ils sont différents. Il en est de même pour deux rationnels. Mais pour deux réels en analyse constructive, on ne dispose pas de méthode générale permettant de prouver que
est valide, car pour tout couple d'entiers, on peut prouver qu'ils sont égaux, ou on peut prouver qu'ils sont différents. Il en est de même pour deux rationnels. Mais pour deux réels en analyse constructive, on ne dispose pas de méthode générale permettant de prouver que 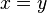 ou de prouver que
ou de prouver que 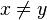 . Cette situation correspond bien aux situations qu'on rencontre en algorithmique, où l’égalité ou l’inégalité entre deux réels peut être non calculable, c'est-à-dire, non décidable.
. Cette situation correspond bien aux situations qu'on rencontre en algorithmique, où l’égalité ou l’inégalité entre deux réels peut être non calculable, c'est-à-dire, non décidable.
Relations entre les règles
Pour mieux comprendre, on remarquera dans ce qui précède, que contrairement à ce qu’il en est dans la logique de Boole, la conjonction 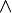 ne peut pas être reformulée en termes de disjonction
ne peut pas être reformulée en termes de disjonction 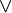 et que le quantificateur existentiel
et que le quantificateur existentiel 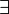 ne peut pas être reformulé en termes de quantificateur universel
ne peut pas être reformulé en termes de quantificateur universel 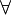 ; ceci en vertu du principe du constructivisme. Dit d’une autre manière et dans des termes peut-être plus proches de l’informatique : il n’est pas permis de réduire les contraintes d’une expression.
; ceci en vertu du principe du constructivisme. Dit d’une autre manière et dans des termes peut-être plus proches de l’informatique : il n’est pas permis de réduire les contraintes d’une expression.
Concernant la disjonction 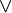 et le quantificateur universel
et le quantificateur universel 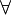 , seules leurs expressions sous formes négatives peuvent être reformulées en termes de, respectivement, conjonction
, seules leurs expressions sous formes négatives peuvent être reformulées en termes de, respectivement, conjonction 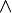 et quantificateur existentiel
et quantificateur existentiel 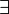 . Cependant, une remarque : il n’est pas possible de contourner cette exigence par l’usage de doubles négations, car (et justement pour cette raison) en logique intuitionniste,
. Cependant, une remarque : il n’est pas possible de contourner cette exigence par l’usage de doubles négations, car (et justement pour cette raison) en logique intuitionniste, 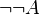 n’est pas équivalent à
n’est pas équivalent à  .
.
Les interprétations des expressions ne se font pas dans le sens de  et
et  , mais dans le sens de Prouvable et Contradictoire. C’est ce qui explique que nous ne disposons pas de tables de calcul, comme avec l’algèbre de Boole, ce qui ensuite, explique pourquoi les opérations ne puissent pas être redéfinies dans les termes d’une autre.
, mais dans le sens de Prouvable et Contradictoire. C’est ce qui explique que nous ne disposons pas de tables de calcul, comme avec l’algèbre de Boole, ce qui ensuite, explique pourquoi les opérations ne puissent pas être redéfinies dans les termes d’une autre.
Interprétation de la logique intuitionniste
Approche intuitive
La logique intutionniste peut être vue comme une logique modale, munie de la modalité de nécessité, notée  où l'implication intuitionniste est
où l'implication intuitionniste est 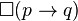 , quand
, quand 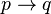 est l'implication classique. Cela peut se lire nécessairement p implique q. L'idée des modèles de Kripke est de créer une hiérarchie qui donne de plus en plus de « nécessité » aux implications. Comme cela ne concerne que l'implication intuitionniste, il n'y a qu'elle qui sera concernée par cette hiérarchie.
est l'implication classique. Cela peut se lire nécessairement p implique q. L'idée des modèles de Kripke est de créer une hiérarchie qui donne de plus en plus de « nécessité » aux implications. Comme cela ne concerne que l'implication intuitionniste, il n'y a qu'elle qui sera concernée par cette hiérarchie.
La sémantique de la logique intuitionniste est fondée sur les modèles de Kripke. Ces modèles sont eux-mêmes fondés sur des mondes dans lesquels opère la sémantique classique (en 0 et 1 pour le calcul des propositions). Ces mondes peuvent être vus comme des contenus d'information de plus en plus riches. Ils sont donc hiérarchisés par une relation d'ordre (la relation d'accessibilité). Si une proposition est « satisfaite » dans un monde, on dit que ce monde force la proposition. Un monde force une proposition 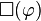 , si tous les mondes qui le dominent hiérarchiquement forcent
, si tous les mondes qui le dominent hiérarchiquement forcent 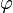 . Comme la nécessité ne va être appliquée qu'à l'implication, nous dirons qu'un monde force
. Comme la nécessité ne va être appliquée qu'à l'implication, nous dirons qu'un monde force  si pour tous les mondes m qui le dominent hiérarchiquement, on a m force
si pour tous les mondes m qui le dominent hiérarchiquement, on a m force 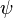 dès que m force
dès que m force 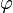 .
.
On dira qu'un modèle de Kripke satisfait ou modèlise une proposition si tous les mondes qu'il contient forcent cette proposition.
Une proposition est valide, si elle est satisfaite par tous les modèles.
On peut montrer que la logique intuitionniste est correcte pour les modèles de Kripke, c'est-à-dire que toute proposition prouvable en logique intuitionniste est valide dans les modèles de Kripke.
Or on peut montrer que les propositions suivantes ne sont pas valides pour les modèles de Kripke :
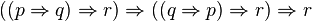 ,
,
-
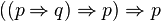 (loi de Peirce).
(loi de Peirce).
On en conclut que ces deux propositions, qui sont pourtant des tautologies classiques, ne sont pas prouvables en logique intuitionniste.
On montre que les modèles de Kripke sont complets pour la logique intuitionniste, c'est-à-dire que toute proposition valide est prouvable.
Approche formelle
Dans cet article nous ne considérons que les modèles de la logique propositionnelle qui forment un exemple de sémantique de Kripke.
Un modèle est formé d'un triplet 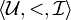 .
.
-
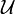 est appelé l'univers et ses éléments notés
est appelé l'univers et ses éléments notés 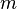 sont appelés des mondes ;
sont appelés des mondes ;
-
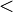 est une relation de pré-ordre ,
est une relation de pré-ordre ,
Un cône est un ensemble 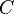 de mondes (
de mondes (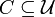 ) tels que
) tels que
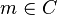 et
et 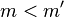 impliquent
impliquent 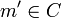 .
.
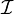 est une initialisation ; c'est une application qui associe à chaque variable propositionnelle un cône de
est une initialisation ; c'est une application qui associe à chaque variable propositionnelle un cône de 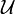 .
.
On définit une relation 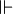 de réalisabilité ou de forçage entre un monde
de réalisabilité ou de forçage entre un monde 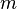 et une proposition
et une proposition 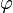 , que l'on écrit
, que l'on écrit 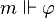 et que l'on lit
et que l'on lit 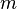 force
force 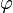 .
La relation de forçage est définie par induction sur la structure des formules.
.
La relation de forçage est définie par induction sur la structure des formules.
- si
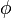 est une variable
est une variable  , alors
, alors 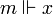 si
si 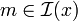 ,
, - si
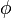 est une proposition
est une proposition 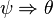 alors
alors 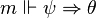 , si pour tout monde
, si pour tout monde  tel que
tel que  on a si
on a si 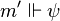 alors
alors 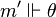 .
.
On peut démontrer (par induction sur la structure ou la taille de 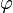 ) que pour chaque proposition
) que pour chaque proposition 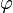 , l'ensemble des
, l'ensemble des 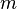 tels que
tels que 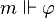 est un cône.
est un cône.
On dit que 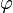 est valide dans
est valide dans 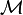 ou que
ou que 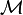 modélise
modélise 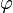 , noté
, noté 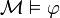 , si pour
, si pour 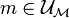 , on a
, on a 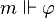 . On dit que
. On dit que 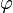 est valide, si pour tout modèle
est valide, si pour tout modèle 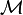 ,
, 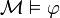 .
.
Pour des compléments brefs de cette section, on peut consulter le paragraphe 4.4 du livre « Introduction à la logique de David, Nour, Raffali », cité dans la bibliographie ci-dessous.
Correction de la logique intuitionniste
On peut montrer que la logique intuitionniste est correcte vis-à-vis des modèles de Kripke, c'est-à-dire que toute proposition démontrable est valide.
Formellement, 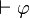 implique
implique 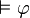 .
.
On peut utiliser ce résultat pour montrer qu'une proposition n'est pas démontrable en logique intuitionniste. Si on considère le modèle 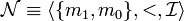 avec
avec 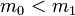 et
et 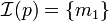 et
et 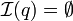 , on peut montrer que
, on peut montrer que 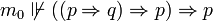 , donc
, donc 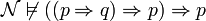 et donc que
et donc que 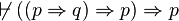 . La loi de Peirce n'est pas valide vis-à-vis des modèles de Kripke, donc elle n'est pas démontrable en logique intuitionniste.
. La loi de Peirce n'est pas valide vis-à-vis des modèles de Kripke, donc elle n'est pas démontrable en logique intuitionniste.
On peut aussi trouver un contre-modèle très simple de la proposition 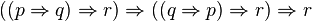 .
.
Complétude de la logique intuitionniste
On peut démontrer que toute proposition valide est démontrable.
Formellement, 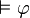 implique
implique 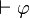 .
.
La démonstration se fait de la façon suivante : si 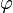 n'est pas démontrable alors on peut construire un contre-modèle (infini) de
n'est pas démontrable alors on peut construire un contre-modèle (infini) de 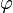 c'est-à-dire un modèle
c'est-à-dire un modèle 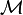 tel que
tel que 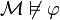 .
.
Relations avec la logique classique
Inclusion de la logique classique dans la logique intuitionniste
Si l’on admet la démonstration faite par Kurt Gödel, que l’insertion de double-négations placées selon des règles définies, nommée « non-non traduction de Gödel-Kolmogorov » (voir ci-après), permet de rendre démontrable en logique intuitionniste toute formule démontrable en logique classique ; et si l’on considère qu’en logique intuitionniste, 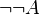 est une forme affaiblie de
est une forme affaiblie de  , alors il est possible d’assimiler la logique classique à une forme affaiblie de la logique intuitionniste et de voir la logique classique comme incluse dans la logique intuitionniste. Remarque : si l’on admet cela, on peut également faire remarquer que la logique intuitionniste n’est pas « moins capable » que la logique classique (voir les exposés qui suivent).
, alors il est possible d’assimiler la logique classique à une forme affaiblie de la logique intuitionniste et de voir la logique classique comme incluse dans la logique intuitionniste. Remarque : si l’on admet cela, on peut également faire remarquer que la logique intuitionniste n’est pas « moins capable » que la logique classique (voir les exposés qui suivent).
De manière plus économe que la saturation des formules et sous-formules par des doubles négations, Gödel a remarqué que si on considère une fonction 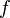 de l'ensemble des formules dans l'ensemble des formules définie par :
de l'ensemble des formules dans l'ensemble des formules définie par :
-
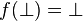
-
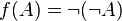 , pour une formule atomique
, pour une formule atomique  différente de ⊥
différente de ⊥ -
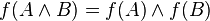
-
![f (A \or B) = \neg \left[ \neg f (A) \and \neg f (B) \right]](../i/m/987f95752d75fabe83ef242818fcd014.png)
-
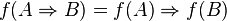
-
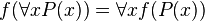
-
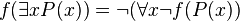
Où  et
et 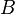 sont des formules quelconques et
sont des formules quelconques et  est une formule ayant
est une formule ayant  comme paramètre.
comme paramètre.
Alors on a le théorème suivant :
-
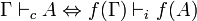 .
.
Où 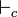 est la déduction classique et
est la déduction classique et 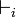 est la déduction intuitionniste.
est la déduction intuitionniste.
La Non-non traduction
|
|
Cette section semble contenir un travail inédit ou des déclarations non vérifiées. Vous pouvez aider en ajoutant des références. Voir la page de discussion pour plus de détails.
|
Ce qui amena Brouwer à concevoir l’intuitionnisme étant une remise en cause de la qualité des preuves de la logique classique[4],
une question peut venir : quelle est donc la valeur d’une preuve de la logique classique du point de vue de la logique intuitionniste ? Dans le cas de la preuve de l’hypothèse qu’il existe des a et b irrationnels tels que ab soit rationnel (voir plus haut), la preuve de cette affirmation par le tiers-exclus est-elle fausse ? Il serait contradictoire de l’affirmer, puisque le théorème de Gelfond-Schneider indique que effectivement, l’une des deux hypothèses utilisées est concrètement vraie, et qu’il existe des solutions qui permettent d’en donner des exemples à l’œuvre. Cependant, comme vu précédemment, elle apporte une réponse… incomplète (elle ne réalise pas de solution). On pourra dire assez honnêtement, que la preuve par le tiers-exclus, montre au moins que l’affirmation de l’hypothèse qu’elle « démontre », n’est pas une contradiction. La preuve de la non-contradiction d’une hypothèse  selon la logique intuitionniste étant la preuve de
selon la logique intuitionniste étant la preuve de 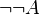 , c’est finalement la preuve de
, c’est finalement la preuve de 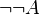 (qui signifie que
(qui signifie que  peut éventuellement être démontré) qu’a effectuée la démonstration par la logique classique. Cette constatation est le fondement de la non-non traduction, qui permet d’exprimer une formule de la logique classique en logique intuitionniste (voir Liens externes). Ce principe a été formalisé par Kurt Gödel et Andreï Kolmogorov.
peut éventuellement être démontré) qu’a effectuée la démonstration par la logique classique. Cette constatation est le fondement de la non-non traduction, qui permet d’exprimer une formule de la logique classique en logique intuitionniste (voir Liens externes). Ce principe a été formalisé par Kurt Gödel et Andreï Kolmogorov.
Attention : la non-non traduction est une traduction dans un seul sens. Bien qu’elle permette de traduire une expression de la logique classique en termes de la logique intuitionniste, elle ne garantit par l’inverse (mais l’inverse reste possible dans certains cas, comme il peut l’être trivialement pour une formule traduite de la logique classique). De plus et ne serait-ce que pour la raison que, par exemple en logique classique 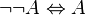 ou encore qu’en logique classique les opérateurs peuvent être exprimés les uns par rapport aux autres, la non-non traduction ne peut pas être bijective : plusieurs expressions de la logique classique peuvent correspondre à une même expression de la logique intuitionniste.
ou encore qu’en logique classique les opérateurs peuvent être exprimés les uns par rapport aux autres, la non-non traduction ne peut pas être bijective : plusieurs expressions de la logique classique peuvent correspondre à une même expression de la logique intuitionniste.
La question des preuves non constructives
Bien que le principe de la logique intuitionniste soit la preuve constructive, nous avons vu qu’il est possible de traduire une expression de la logique classique en logique intuitionniste. Cela amène à se poser la question des expressions de la logique intuitionniste, qui correspondraient à des expressions de la logique classique (suite à une traduction ou non). Nous avons vu que ces expressions peuvent faire usage de 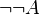 qui signifie que
qui signifie que  n’est pas contradictoire. Les preuves faites sur de telles expressions ne traiteront pas de choses concrètes, mais de potentialités (contradictoire ou non contradictoire) ; ce qui n’amène pas à exposer une solution au sens propre du terme, puisque l’objet, est la proposition. La logique intuitionniste, peut donc également faire des démonstrations non constructives ; mais ces démonstrations sont alors identifiées comme telles, et ne disent rien de plus que « cela est contradictoire » ou « cela n’est pas contradictoire ». La logique intuitionniste peut donc produire des preuves ayant sens pour la logique classique. Une interprétation de cette remarque, est que la logique intuitionniste, éclaire ce que fait la logique classique, en donnant une interprétation de ce que sont les preuves classiques.
n’est pas contradictoire. Les preuves faites sur de telles expressions ne traiteront pas de choses concrètes, mais de potentialités (contradictoire ou non contradictoire) ; ce qui n’amène pas à exposer une solution au sens propre du terme, puisque l’objet, est la proposition. La logique intuitionniste, peut donc également faire des démonstrations non constructives ; mais ces démonstrations sont alors identifiées comme telles, et ne disent rien de plus que « cela est contradictoire » ou « cela n’est pas contradictoire ». La logique intuitionniste peut donc produire des preuves ayant sens pour la logique classique. Une interprétation de cette remarque, est que la logique intuitionniste, éclaire ce que fait la logique classique, en donnant une interprétation de ce que sont les preuves classiques.
La question du tiers-exclu
Le fait que la négation  n’ait pas le même sens en logique intuitionniste qu’en logique classique explique que
n’ait pas le même sens en logique intuitionniste qu’en logique classique explique que 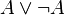 ne soit pas toujours valide en logique intuitionniste (après tout, des similitudes syntaxiques n’indiquent pas nécessairement des similitudes sémantiques). Cependant, il existe une formulation du tiers-exclu de la logique classique, qui est (en termes intuitionnistes)
ne soit pas toujours valide en logique intuitionniste (après tout, des similitudes syntaxiques n’indiquent pas nécessairement des similitudes sémantiques). Cependant, il existe une formulation du tiers-exclu de la logique classique, qui est (en termes intuitionnistes) 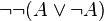 . Cette expression reste toujours valide, même si
. Cette expression reste toujours valide, même si  n’est pas décidable (c’est une conséquence de la signification du
n’est pas décidable (c’est une conséquence de la signification du 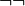 , qui a été présenté plus haut). Cette interprétation, « même si
, qui a été présenté plus haut). Cette interprétation, « même si  n’est pas décidable
n’est pas décidable 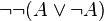 est toujours démontrable », est une autre mise en lumière de la raison pour laquelle le tiers-exclu classique ne peut pas fonder une preuve intuitionniste : son interprétabilité est faible.
est toujours démontrable », est une autre mise en lumière de la raison pour laquelle le tiers-exclu classique ne peut pas fonder une preuve intuitionniste : son interprétabilité est faible.
Références
- ↑ Alexandre Miquel, « L’intuitionnisme : où l’on construit une preuve », Pour la Science, no 49 « Argumentation et preuve », , p. 33, cadre B (lire en ligne).
- ↑ (en) Dirk van Dalen (de), Logic and structure, Springer, 1991, p. 155.
- ↑ Joseph Vidal-Rosset, « Intuitionnisme », Université de Nancy 2, (sur l’interprétation des expressions et la philosophie).
- ↑ Franck Wynen, « La logique intuitionniste », CNAM, 2000-2001 (sur l’épistémologie et l’histoire de la logique intuitionniste de Platon au XXe siècle).
Annexes
Bibliographie
Ouvrages
- Jean-Yves Girard, Le point aveugle, Tome I, Hermann, 2007.
- Jean Largeault, L'Intuitionisme, Paris, Presses universitaires de France, 1992.
- Jean Largeault, Intuitionisme et théorie de la démonstration, Paris, J. Vrin, , 566 p. (ISBN 2-7116-10594, présentation en ligne) Textes de Bernays, Brouwer, Gentzen…[et al.] réunis, traduits et présentés par Jean Largeault.
- René David, Karim Nour et Christophe Raffali, Introduction à la logique, Dunod, 2001.
Liens externes
- Richard Moot et Christian Retoré, « La "non-non" traduction de Gödel-Kolmogorov », Université Bordeaux I,
- Étienne Lozes, « TD non non traduction », Laboratoire Spécification et Vérification — ENS Cachan,
- Alexandre Miquel, « Réalisabilité et extraction de programmes », Laboratoire Preuves, Programmes et Systèmes (PPS) de Jussieu, (sur la logique intuitionniste et l’interprétation de Brouwer-Heyting-Kolmogorov — interprétation BHK)
Articles connexes
- Algèbre de Heyting (en)
- Analyse constructive
- Constructivisme (mathématiques)
- Sémantique de Kripke
- Portail de la philosophie
- Portail de la logique