Logique classique

Cet article est une ébauche concernant la logique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Consultez la liste des tâches à accomplir en page de discussion.

La logique classique est la première formalisation du langage et du raisonnement mathématique développée à partir de la fin du XIX^e siècle en logique mathématique. Appelée simplement logique à ses débuts, c'est l'apparition d'autres systèmes logiques formels, notamment pour la logique intuitionniste, qui a suscité l'adjonction de l'adjectif classique au terme logique.

La logique classique est caractérisée par des postulats qui la fondent et la différencient de la logique intuitionniste, exprimés dans le formalisme du calcul des propositions ou du calcul des prédicats :

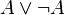
Le tiers exclu énonce que pour toute proposition mathématique considérée, elle-même ou sa négation est vraie : $A\or \neg A$

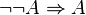
Le raisonnement par l'absurde : $\lnot\neg A \Rightarrow A$

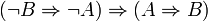
La contraposition : $\big(\neg B \Rightarrow \neg A\big) \Rightarrow \big(A \Rightarrow B\big)$

L'implication matérielle : $(A\Rightarrow B) \Leftrightarrow (\neg A\or B)$

Ces principes sont équivalents par raisonnement intuitionniste, c’est-à-dire que l'on peut montrer que n'importe lequel d'entre eux permet de déduire les autres en utilisant les règles intuitionnistes.

On y ajoute généralement l'une des lois de De Morgan : 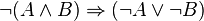$\neg(A\and B) \Rightarrow (\neg A\or \neg B)$

Ces principes contribuent au fait que les modèles calculatoires de la logique classique sont beaucoup plus complexes que ceux de la logique intuitionniste.

Le principe

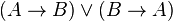
(A \to B) \vee (B \to A)

est valide en logique classique, et n'est pas démontrable en logique intuitionniste^[1], mais son adjonction à la logique intuitionniste n'engendre pas la logique classique^{[réf. souhaitée]}.

Notes et références

↑ (en) Dirk van Dalen (de), Logic and Structure, chap. 5 « Intuitionistic logic », exercice 9. (a), Springer-Verlag, 1991.

Lien externe

Rappel : Bases de : logique, ensembles, limites.

Articles liés

Calcul des propositions
Calcul des prédicats
Déduction naturelle
Logique intuitionniste
Logique linéaire notamment les lois de De Morgan
Logique minimale

Portail des mathématiques
Portail de la logique

This article is issued from Wikipédia - version of the Thursday, June 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Logique classique

Notes et références

Lien externe

Articles liés

Medical Encyclopedia