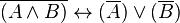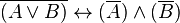Lois de De Morgan

Représentation graphique des lois de De Morgan

Les lois de De Morgan sont des identités entre propositions logiques. Elles ont été formulées par le mathématicien britannique Augustus De Morgan (1806-1871).

Énoncé en français

La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie non(A et B) est (non A) ou (non B).

La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que non(A ou B) est (non A) et (non B).

Énoncé mathématique

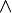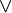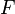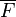Sachant que la conjonction s'exprime par le signe : $\land$ , la disjonction s'exprime par le signe : $\lor$ et la négation d'une formule $F$ s'écrit $\overline{{F}}$ .

$\overline{(A \land B)} \leftrightarrow (\overline{A})\lor (\overline{B})$

$\overline{(A \lor B)} \leftrightarrow (\overline{A}) \land (\overline{B})$

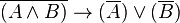
De ces quatre implications valides en logique classique, trois sont valides en logique intuitionniste, mais pas : $\overline{(A \land B)} \rightarrow (\overline A)\lor (\overline B)$

Justification

Pour justifier ces formules, on peut par exemple, utiliser la méthode sémantique des tables de vérité. On rappelle que deux formules sont équivalentes si et seulement si elles ont la même table de vérité.

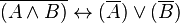$\overline {(A \land B)} \leftrightarrow (\overline A) \lor (\overline B)$
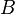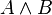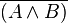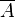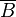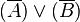$A$	$B$	$A \land B$	$\overline{(A \land B)}$	$\overline{A}$	$\overline B$	$(\overline A) \lor (\overline B)$
0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	0	1	1
1	1	1	0	0	0	0

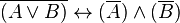$\overline{(A \lor B)} \leftrightarrow (\overline A) \land (\overline B)$
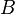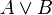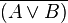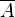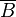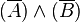$A$	$B$	$A \lor B$	$\overline {(A \lor B)}$	$\overline A$	$\overline B$	$(\overline A) \land (\overline B)$
0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

Généralisation

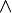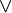Les énoncés de De Morgan se généralisent à n propositions par récurrence, en utilisant l'associativité des lois $\land$ et $\lor$ ainsi que leur double distributivité. Comme les deux preuves sont symétriques (il suffit de remplacer une loi par l'autre), on ne donne ici que celle pour la première loi.

Vrai au rang n=2
Si vrai au rang n

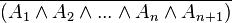
$\overline{(A_1 \land A_2 \land ... \land A_n \land A_{n+1})}$

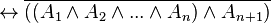
$\leftrightarrow \overline{( (A_1 \land A_2 \land ... \land A_n) \land A_{n+1})}$

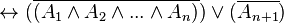
$\leftrightarrow (\overline{(A_1 \land A_2 \land ... \land A_n)}) \lor (\overline{A_{n+1}})$

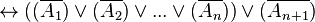
$\leftrightarrow ((\overline{A_1}) \lor (\overline{A_2}) \lor ... \lor (\overline{A_n})) \lor (\overline {A_{n+1}})$

La généralisation de ces règles au-delà du fini donne les règles d'interdéfinissabilité des quantificateurs universel et existentiel du calcul des prédicats classique. Le quantificateur universel pouvant être vu comme une généralisation de la conjonction et le quantificateur existentiel pouvant être vu comme une généralisation de la disjonction (non exclusive).

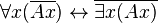
$\forall x (\overline{Ax}) \leftrightarrow \overline {\exists x (Ax)}$

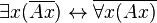
$\exist x (\overline{Ax}) \leftrightarrow \overline {\forall x (Ax)}$

Et de ces quatre implications classiques, seule 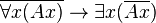$\overline {\forall x (Ax)} \rightarrow \exists x ( \overline{Ax} )$ n'est pas valide en logique intuitionniste.

Voir aussi

Portail de la logique
Portail des mathématiques