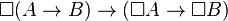Logique modale

Des informations de cet article ou section devraient être mieux reliées aux sources mentionnées dans la bibliographie ou en liens externes.

Améliorez sa vérifiabilité en les associant par des références.

Cet article n’est pas rédigé dans un style encyclopédique.

Vous pouvez améliorer sa rédaction !

La logique modale est un type de logique qui permet de formaliser des éléments modaux, c'est-à-dire de spécifier des qualités du vrai.

Exemple d'éléments modaux : « il est possible », « il est nécessaire », etc.

Par exemple, on peut utiliser la proposition « Il pleut » comme ceci :

Il est possible qu’il pleuve ;
Il est démontré qu’il est faux qu’il pleuve ;
Il n’est pas permis qu’il pleuve.

La logique modale est à l'origine de la logique aléthique qui prend en compte la croyance du locuteur comme dans la phrase: Christophe Colomb croit se trouver en Asie.

Logique modale aléthique

En logique modale aléthique (ou aristotélicienne, ou classique), on dégage quatre modalités :

nécessaire (ce qui ne peut pas ne pas être vrai), noté $\Box$ ;
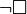contingent (ce qui peut être vrai ou faux), noté $\neg \Box$ ;
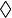possible (tout ce qui peut être, sauf impossible), noté $\Diamond$ ;
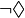impossible (ce qui ne peut pas ne pas être faux), noté $\neg \Diamond$ .

Ces 4 modalités sont liées, il suffit d'une pour définir les trois autres.

L'interprétation intuitive (non partagée par toute la communauté philosophico - logicienne) est la suivante :

Nécessaire ≡ impossible pas ;
Contingent ≡ non nécessaire ≡ possible pas ;
Possible ≡ non impossible.

On distingue donc deux connecteurs unaires duaux l'un de l'autre :

Le nécessaire $\Box$ ;
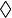Le possible $\Diamond$ .

Ils s'ajoutent aux deux connecteurs unaires classiques du vrai et du faux : respectivement ⊤ et ⊥.

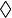$\Box$ p signifie que p est assurément vrai, tandis que $\Diamond$ p signifie que p est possiblement vrai, c'est-à-dire compatible avec les connaissances actuelles.

Exemples :

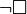$\neg \Box$ trav : il n’est pas nécessaire que les élèves travaillent ;
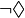$\neg \Diamond$ trav : il n’est pas possible que les élèves travaillent ;
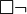$\Box \neg$ trav : il est nécessaire que les élèves ne travaillent pas ;
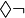$\Diamond \neg$ trav : il est possible que les élèves ne travaillent pas.

En logique modale aléthique (ou aristotélicienne, ou classique), nous pouvons exprimer les quatre opérateurs à l’aide d’un seul (ici la nécessité) et de la négation. Ainsi :

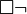Impossible est $\square \neg$ ;
Possible est $\neg \square \neg$ .

Une proposition nécessaire ne peut pas être fausse sans impliquer de contradiction, a contrario d’une proposition contingente qui peut impliquer une contradiction.

La logique intuitionniste peut être construite sur la logique aléthique comme une logique modale.

Différentes logiques modales

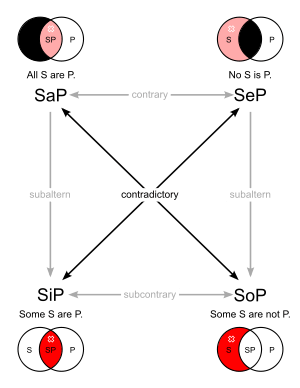
Le carré modal : relations entre les modalités de la logique aristotélicienne.

Il existe plusieurs types de logiques modales, dont les modes sont :

classiques (ou aristotéliciens, ou aléthiques) :
- nécessaire, noté $\Box$
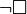
- contingent, noté $\neg \Box$
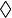
- possible, noté $\Diamond$
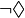
- impossible, noté $\neg \Diamond$
épistémiques (relatifs à la connaissance) :
- connu par l'agent 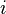$i$ , noté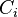 $C_i$
- contestable
- exclu
- plausible
- connaissance commune du groupe $G$ d'agents, notée $CK_G$
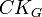
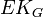- connaissance partagée du groupe $G$ d'agents, notée $EK_G$ (chacun sait)
déontiques (moraux) :
- obligatoire, noté O
- interdit, noté I
- permis, noté P
- facultatif, noté F
temporels :
- toujours, noté $\Box$
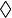
- un jour, noté $\Diamond$
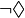
- jamais, noté $\neg \Diamond$
- demain, noté X
- jusqu'à ce que, opérateur binaire noté U
- désormais, noté G
- un jour futur, noté F
- toujours dans le passé, noté H
- un jour passé, noté P
doxastiques (sur les croyances) :
- cru, noté B
- croyance commune du groupe $G$ d'agents, notée $CB_G$
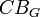
contrefactuels :
- Si A était vrai, où l'on sait que A n'est pas vrai.
dynamiques (effet d'actions, notées a, sur des propositions) :
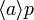
- Il existe une exécution de a tel qu'après a, p est vrai, noté $\langle a\rangle p$
- p est vrai après toute exécution de a, noté $[a] p$ .

Axiomes de logique modale

Chaque logique modale est munie d'une série d'axiomes qui définissent le fonctionnement des modalités. Une logique modale est dite normale ou de Kripke si et seulement si elle admet

(RN) (ou (N) ou (NEC)) la règle d'inférence de nécessitation :

Si A est un théorème, alors

\Box A

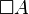aussi.

(K) l'axiome de distribution de Kripke :

\Box(A\rightarrow B) \rightarrow( \Box A \rightarrow \Box B)

En ajoutant d'autres types d'axiomes on obtient d'autres types de logique modale :

(D) : 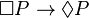$\Box P \rightarrow \Diamond P$ soit la nécessité implique la possibilité (en logique aristotélicienne)
(T) (ou (M)): 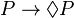$P \rightarrow \Diamond P$ soit le fait implique la possibilité
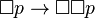
(4) : $\Box p\rightarrow\Box\Box p$
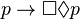
(B) : $p\rightarrow\Box\Diamond p$
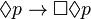
(5) (ou (E)) : $\Diamond p\rightarrow\Box\Diamond p$

Ces axiomes permettent de définir les systèmes suivants :

K:=K+RN

T:=K+T

S4:=T+4

S5:=S4+B ou T+5

D:=K+D

La suite de systèmes K à S5 forme une hiérarchie imbriquée qui compose le noyau de la logique modale normale. L'axiome D, quant à lui, est principalement utilisé dans les logiques déontique, doxastique et épistémique.

Modèles de la logique modale

Article détaillé : Sémantique de Kripke.

Les modèles de Kripke, ou modèles de mondes possibles, donnent une sémantique aux logiques modales. Notons 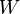$W$ l'ensemble des mondes possibles et 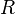$R$ une relation binaire entre les mondes possibles appelée relation d'accessibilité. Une valuation 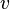$v$ affecte à chaque variable propositionnelle une valeur de vérité et ce pour chaque monde possible. 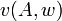$v(A,w)$ dénote la valeur de vérité de la proposition $A$ dans le monde $w$ .

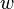La sémantique d'un opérateur modal est définie à partir d'une relation d'accessibilité de la façon suivante :

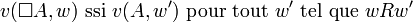
$v(\square A,w) \text{ ssi } v(A,w') \text{ pour tout } w' \text{ tel que } wRw'$

Classification des systèmes de logique modale

Les systèmes de logiques modales sont organisés en fonction des règles d'inférence et des axiomes qui les caractérisent.

Logiques modales classiques

Les systèmes de logique modale classiques sont ceux qui acceptent la règle d'inférence suivante :

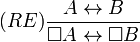
$(RE) \frac{A \leftrightarrow B}{\Box A \leftrightarrow \Box B}$

L'usage veut que l'on donne à un tel système un nom canonique du type 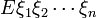$E \xi_1 \xi_2 \cdots \xi_n$ , où les 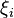$\xi_i$ sont les noms des axiomes du systèmes.

Logiques modales monotones

Les systèmes de logique modale monotones sont ceux qui acceptent la règle d'inférence RM :

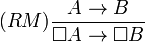
$(RM) \frac{A \to B}{\Box A \to \Box B}$

L'ensemble des systèmes monotones est inclus dans l'ensemble des systèmes classiques.

Logiques modales régulières

Les systèmes de logique modale réguliers sont ceux qui acceptent la règle d'inférence RR :

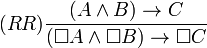
$(RR) \frac{(A \wedge B) \to C}{(\Box A \wedge \Box B) \to \Box C}$

L'ensemble des systèmes réguliers est inclus dans l'ensemble des systèmes monotones.

Logiques modales normales

Les systèmes de logique modale normaux sont ceux qui acceptent la règle d'inférence RK :

$(RK) \frac{(A_1 \wedge \cdots A_n) \to B}{(\Box A_1 \wedge \cdots \Box A_n) \to \Box B}$

L'ensemble des systèmes normaux est inclus dans l'ensemble des systèmes réguliers.

Une définition équivalente et plus courante des systèmes normaux est la suivante : un système de logique modal est dit normal s'il comporte l'axiome (K) et accepte la règle de nécessitation (RN) comme règle d'inférence :

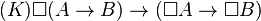
$(K) \Box (A \to B) \to (\Box A \to \Box B)$

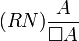
$(RN) \frac{A}{\Box A}$

Les systèmes normaux sont les plus utilisés, car ce sont ceux qui correspondent aux sémantiques de Kripke. Il est cependant possible de trouver des sémantiques pour des logiques classiques non normales, mais elles présentent en général de moins bonnes propriétés.

Voir aussi

Liens externes

(en) James Garson, Modal Logic, The Stanford Encyclopedia of Philosophy, Edward N. Zalta (ed.), 2007.
(en) S4 prover by tableaux method, S4 prover

Bibliographie

(en) Patrick Blackburn, Maarten de Rijke et Yde Venema, Modal Logic,‎ 2001 [détail des éditions]
(en) Brian F. Chellas, Modal logic, an introduction, Cambridge University Press,‎ 1980 [détail de l’édition]
L. Fontaine, Logiques modales et anthropologie. Des règles à la parole chez les Indiens yucuna d'Amazonie colombienne. L'Homme, n.184, 2007, 131-153.
P. Gochet, P. Gribomont, A. Thayse, Logique, Vol.3 : méthodes pour l'intelligence artificielle, Paris, Hermès-Lavoisier, 2000, 394p. (Résumé très complet en français des principales logiques modale).

Portail de la logique
Portail de la philosophie
Portail de la philosophie analytique

This article is issued from Wikipédia - version of the Thursday, June 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.