Finesse (aérodynamique)
La finesse est une caractéristique aérodynamique; c'est le rapport entre la portance et la traînée.
Elle est souvent désignée par le terme anglophone L/D ratio (Lift/Drag ratio = rapport portance/traînée).
On définit aussi la finesse comme le rapport 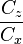 , à condition que ces deux coefficients soient rapportés à la même surface.
, à condition que ces deux coefficients soient rapportés à la même surface.
Définition
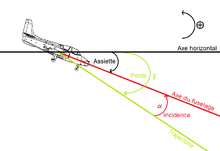
La finesse d'un aérodyne à voilure fixe est le rapport entre sa portance et sa traînée aérodynamique. En vol plané (sans force de traction/propulsion) à vitesse vraie (vitesse de l'aéronef par rapport à la masse d'air dans laquelle il se déplace) constante, et donc à pente constante, elle est égale au rapport entre la distance horizontale parcourue et la hauteur de chute ou encore au rapport entre la vitesse horizontale et la vitesse verticale (taux de chute). Bien sûr, cette définition est à adapter suivant l'objet étudié: voile de bateau, profil de carène...
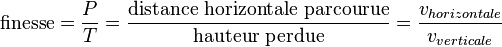
Pour un aérodyne donné, la finesse varie en fonction de l'incidence de l'aile. Cependant, comme le coefficient de portance varie aussi avec l'angle d'incidence, pour obtenir une portance équivalente au poids, il faut adapter la vitesse. C'est pourquoi la finesse varie avec la vitesse.
Dans le cas d'un planeur, la finesse varie en fonction de la vitesse sur trajectoire en suivant une courbe qu'on appelle la polaire des vitesses.
Cette courbe représente le taux de chute en fonction de la vitesse sur trajectoire (ou « vitesse indiquée »). Elle est croissante entre la valeur de la vitesse de décrochage jusqu'à la valeur de la vitesse correspondant au taux de chute minimal, puis décroissante au-delà.
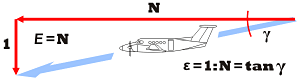
À vitesse constante, la 
Par exemple, une finesse de 7 correspond à un angle de plané de ~8° ;
Valeurs typiques
Les avions ont généralement des finesses comprises entre 8 et 15, rarement plus de 20 :
- les avions de ligne ont des finesses comprises entre 15 et 20
- le Concorde avait une finesse de 4 au décollage, 11.5 à Mach 0.95 et 7.3 à Mach 2.
Les derniers prototypes de "wingsuit" permettent d'atteindre une finesse de 3.
Les parapentes modernes ont une finesse comprise entre 9 et 13[1].
Les deltaplanes "souples" modernes ont une finesse comprise entre 14 et 16.
Les deltaplanes "rigides" modernes ont une finesse comprise entre 18 et 22.
Les planeurs de construction en bois et toile de 27 à 32.
les Planeurs plastiques ont commencé à 30 et sont à plus de 60 actuellement. Les "Aigles blancs"
Typiquement, sur un planeur moderne :
- la vitesse de finesse maximale se situe entre 80 et 120 km/h selon le modèle et la charge alaire[2],[3],
- la vitesse de taux de chute minimal est de l'ordre de 80 km/h et le taux de chute correspondant de l'ordre de 0,8 à 0,5 m/s,
- la vitesse de décrochage est de l'ordre de 70 km/h.
Finesse commune comprise entre 40 et 60.
Les Avions à Propulsion Humaine, qui permettent de voler en pédalant, auraient une finesse théorique supérieure à 130 (calcul de l'institut de maintenance aéronautique de l'Université de Bordeaux)[4].
Équivalence entre les définitions
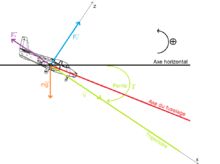
Système : avion
Référentiel : terrestre supposé galiléen
Bilan des forces extérieures au système:
- Portance
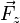 perpendiculaire à la vitesse de déplacement de l'avion
perpendiculaire à la vitesse de déplacement de l'avion
- Traînée
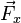 opposée à la vitesse de déplacement de l'avion
opposée à la vitesse de déplacement de l'avion
- Poids
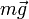
D'après la deuxième loi de Newton on a :
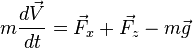
On suppose que l'aéronef est en mouvement non accéléré et l'on a donc :
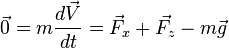
Cela se traduit donc en projetant sur chacun des axes par :
Sur Ox : 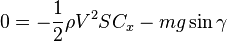
Sur Oz : 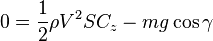
Et donc, pour un vol plané à vitesse vraie constante :
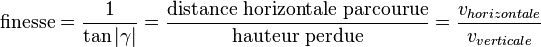
Et donc :
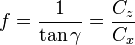
Pour un planeur, on pourra aisément écrire que 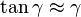 . Cependant cela ne sera pas correct pour un wingsuit qu'on pourrait presque assimiler à un « fer à repasser ».
. Cependant cela ne sera pas correct pour un wingsuit qu'on pourrait presque assimiler à un « fer à repasser ».
Finesse air et Finesse sol
La finesse air d'un aéronef est donnée par rapport à la masse d'air dans laquelle il se déplace. C'est souvent celle que le constructeur annonce car elle est indépendante du vent.
La finesse sol, elle, est calculée par rapport au sol (c'est souvent la plus intéressante : c'est celle qui détermine si un parcours jusqu'à un but est possible ou non). Cette finesse doit tenir compte du déplacement de l'air (du vent) par rapport au sol.
Quand l'aéronef se déplace dans la direction et le sens du vent la finesse sol augmente et inversement. Par vent fort de face, l'aéronef peut avoir une vitesse sol et une finesse sol faibles ou négatives, ce qui sera d'ailleurs souvent une raison suffisante pour annuler le vol.
Finesse air et finesse sol sont égales lorsque l'air est calme et ne subit aucun mouvement vertical ni horizontal.
Calcul de la finesse maximale
Relation entre la traînée induite et la traînée parasite

On va montrer qu'un aéronef atteint sa finesse maximale lorsque la traînée induite est égale à la traînée parasite.
La traînée parasite 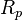 causée par la résistance de l'air peut s'écrire sous la forme
causée par la résistance de l'air peut s'écrire sous la forme
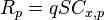
où 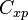 est le coefficient de traînée parasite et on a
est le coefficient de traînée parasite et on a 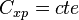 . Soit
. Soit 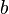 l'envergure de l'aile et
l'envergure de l'aile et  sa corde moyenne (~ largeur moyenne de l'aile).
sa corde moyenne (~ largeur moyenne de l'aile). 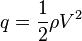 est la pression dynamique.
est la pression dynamique.
On pose 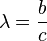 l'allongement de l'aile. On rappelle que
l'allongement de l'aile. On rappelle que 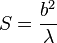
On note 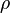 la masse volumique de l'air. On obtient :
la masse volumique de l'air. On obtient :
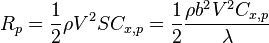
La traînée induite 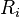 s'exprime comme suit :
s'exprime comme suit :
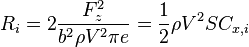 avec
avec 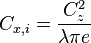
où 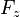 est la portance,
est la portance, 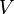 est la vitesse de l'aéronef et
est la vitesse de l'aéronef et  est le coefficient d'Oswald. Cette dernière formule provient de la théorie des profils minces.
est le coefficient d'Oswald. Cette dernière formule provient de la théorie des profils minces.
Lorsqu'un avion ou planeur est en vol, la traînée induite 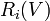 et la traînée parasite
et la traînée parasite 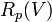 s'ajoutent et constituent la traînée totale :
s'ajoutent et constituent la traînée totale :
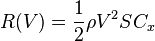 avec
avec 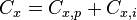
Pour ne pas alourdir les calculs avec des racines carrés dans la suite on exprimera non pas la finesse 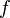 , mais la finesse au carré et on a alors :
, mais la finesse au carré et on a alors :
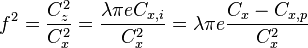
On dérive par rapport à 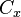 :
:
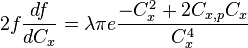
Pour que 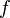 soit maximale il faut que
soit maximale il faut que 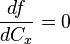 ce qui revient ici à déterminer les racines d'un polynôme du second degré en
ce qui revient ici à déterminer les racines d'un polynôme du second degré en 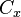 .
.
On obtient donc que 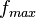 est atteinte quand
est atteinte quand 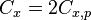 c'est-à-dire :
c'est-à-dire :
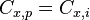 et donc
et donc 
Ce qui signifie que la traînée induite est égale à la traînée parasite.
Démonstration simplifiée pour un planeur
Dans les cours d'aérodynamique pour pilotes, il est souvent affirmé sans justification que la traînée induite est proportionnelle à 1/V² et que la traînée parasite est proportionnelle à V². Dans ces conditions, la démonstration du théorème ci-dessus devient triviale qui est alors un simple corollaire des postulats énoncés ci-dessus. Dans ce qui suit, les postulats vont être démontrés et l'on va en conclure le théorème ci-dessus.
Les planeurs ont des angles de plané qui sont très petits et l'on peut donc supposer que 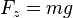
La traînée induite 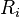 s'exprime comme suit :
s'exprime comme suit :
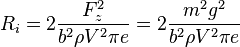
La traînée parasite 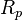 causée par la résistance de l'air peut s'écrire sous la forme
causée par la résistance de l'air peut s'écrire sous la forme
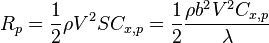
Lorsqu'un planeur est en vol, la traînée induite 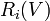 et la traînée parasite
et la traînée parasite 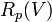 s'ajoutent et constituent la traînée totale R(V). La finesse d'un planeur sera optimale lorsque la traînée totale R(V) est minimale. On résout donc
l'équation
s'ajoutent et constituent la traînée totale R(V). La finesse d'un planeur sera optimale lorsque la traînée totale R(V) est minimale. On résout donc
l'équation
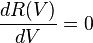
On définit 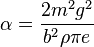 et
et 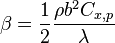 .
On peut écrire symboliquement :
.
On peut écrire symboliquement :
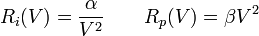
Après avoir calculé la dérivée de R(V), on résout donc:
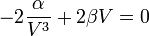
Et donc en multipliant la relation ci-dessus par V, on obtient :
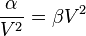
ce qui signifie que la traînée induite est égale à la traînée parasite.
Vitesse optimale
On pose 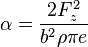 et
et 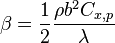 . On a alors :
. On a alors :
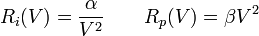
Le planeur atteindra sa finesse maximale en air calme lorsque la traînée induite sera égale à la traînée parasite, c'est-à-dire :
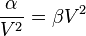
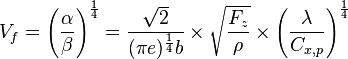
Calcul de la finesse maximale (d'un planeur)
Un planeur n'a pas de moteur; il est « propulsé » par ses ailes[note 1] sous l'effet de la gravité. Soit f(V) la finesse du planeur défini par le rapport de la vitesse horizontale à la vitesse verticale. Soit 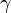 l'angle de plané. Comme
l'angle de plané. Comme 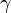 est petit, on peut écrire que
est petit, on peut écrire que 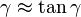 et donc que :
et donc que :
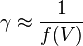
Quand le planeur est en équilibre, en mouvement non accéléré, on a :
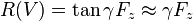
De plus, la finesse maximale est une caractéristique de l'aéronef et est donc constante (tant que les caractéristiques de l'aéronef sont inchangées).
Dans ce qui suit, on démontre cette assertion qui ne semble pas évidente. On rappelle que lorsque la planeur atteint sa finesse maximale la traînée induite est égale à la traînée parasite. On obtient donc :
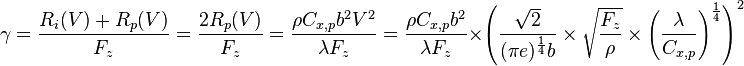
Et donc :
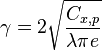
Et donc :
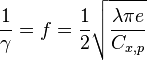
Comme annoncé ci-dessus, la finesse maximale ne dépend pas de la masse du planeur et ni de la densité de l'air environnant. Elle dépend uniquement de l'aérodynamisme du planeur et de sa géométrie (allongement) : la finesse maximale est une caractéristique de l'aéronef et est donc constante. Ceci justifie a posteriori que la vitesse de chute du planeur augmentera en même temps que sa masse. Donc, lorsque les conditions aérologiques sont moins favorables[note 2], il est préférable de minimiser la masse du planeur pour minimiser la vitesse de chute et donc de ne pas ajouter d'eau dans les ailes ou, si l'on est déjà en vol, de vidanger les ailes.
De plus, plus 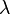 est grand, plus
est grand, plus 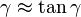 sera petit. Donc, les planeurs ayant des grandes ailes, pour une surface alaire équivalente, aura un plus petit angle de plané et donc une plus grande finesse. Ceci est la raison pour laquelle certains planeurs de compétition en classe libre peuvent avoir jusqu'à 30 mètres d'envergure.
sera petit. Donc, les planeurs ayant des grandes ailes, pour une surface alaire équivalente, aura un plus petit angle de plané et donc une plus grande finesse. Ceci est la raison pour laquelle certains planeurs de compétition en classe libre peuvent avoir jusqu'à 30 mètres d'envergure.
Effet de la masse sur la vitesse optimale
Cette section suppose que l'aéronef a une finesse suffisante pour que l'on puisse supposer que 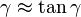 .
.
On considère un planeur de masse 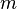 volant à sa vitesse de finesse maximale
volant à sa vitesse de finesse maximale 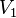 . Le poids du planeur est donné par
. Le poids du planeur est donné par 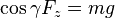 . Pour simplifier la discussion, on suppose que
. Pour simplifier la discussion, on suppose que 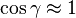 . On a donc :
. On a donc :
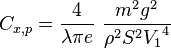
On considère maintenant le même planeur auquel on a ajouté de l'eau et qui a une masse 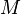 et une vitesse de finesse maximale
et une vitesse de finesse maximale 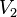 .
On a alors :
.
On a alors :
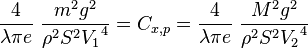
Donc,
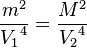
Donc,
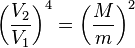
et donc:
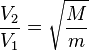 .
.
On constate que la vitesse optimale varie donc comme la racine carrée de la masse du planeur.
En augmentant la masse, on augmente donc aussi la vitesse de finesse maximale mais la valeur de la finesse maximale elle reste constante. La finesse étant égale au taux de chute, ceci signifie que le même planeur auquel on ajoute de l'eau aura la même portée, mais volera plus vite pour maintenir son taux de chute constant.
Polaire des vitesses
On évalue maintenant la vitesse de chute en fonction de la vitesse horizontale pour n'importe quelle vitesse. On a:
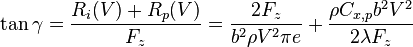
La polaire des vitesses exprime la vitesse de chute 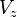 en fonction de la vitesse horizontale. Etant donné que
en fonction de la vitesse horizontale. Etant donné que 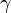 est très petit, on a :
est très petit, on a : 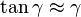
On peut donc considérer que 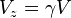 . Donc,
. Donc,
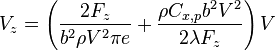
Cette formule exprime la polaire des vitesses. On constate que pour 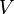 grand, la finesse décroît comme le carré de la vitesse horizontale.
grand, la finesse décroît comme le carré de la vitesse horizontale.
On notera que 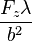 est la charge alaire qui est souvent exprimée en daN/m2 ou plus incorrectement en
kgf/m2. Si l'on appelle P cette charge alaire (qui est homogène à une pression), on obtient :
est la charge alaire qui est souvent exprimée en daN/m2 ou plus incorrectement en
kgf/m2. Si l'on appelle P cette charge alaire (qui est homogène à une pression), on obtient :
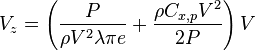
Vitesse de chute à finesse maximale
On a :
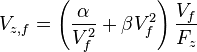
Comme 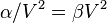 à finesse maximale, on obtient donc :
à finesse maximale, on obtient donc :
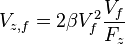
En substituant β, on obtient
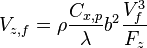
On remplace Vf et donc,
![V_{z,f} = \rho {C_{x,p} \over \lambda} {b^2 \over F_z} \left[
{\sqrt{2} \over (\pi e)^{1 \over 4} b} \times \sqrt{F_z \over \rho} \times \left({\lambda \over C_{x,p}}\right)^{1 \over 4}\right]^3 =
\left({C_{x,p} \over \lambda}\right)^{1 \over 4} {2 \sqrt{2} \over (\pi e)^{3 \over 4}} {1 \over b} \sqrt{F_z \over \rho}](../i/m/fd9ef289248b8260e2bf0e472f3f8873.png)
On note que :
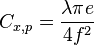
En substituant, on obtient :
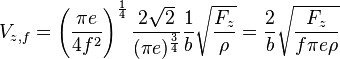
Vitesse de chute minimum
En reprenant les notations ci-dessus, on a :
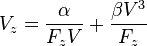
On appelle vitesse minimale 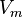 la vitesse horizontale pour laquelle le taux de chute minimal est atteint. Elle est atteinte lorsque
la vitesse horizontale pour laquelle le taux de chute minimal est atteint. Elle est atteinte lorsque 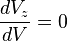 . On obtient donc :
. On obtient donc :
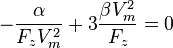
Soit 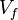 la vitesse à finesse maximale. Donc,
la vitesse à finesse maximale. Donc,
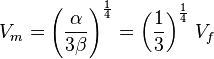
On obtient donc :
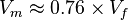
On a :
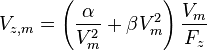
On a 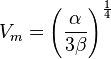 et donc
et donc
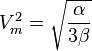 que l'on substitue et donc,
que l'on substitue et donc,
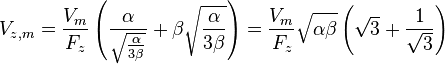
On substitue Vm et donc,
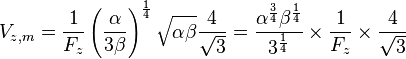
On substitue maintenant α et β et donc,
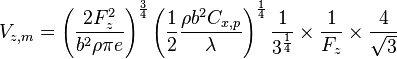
On obtient donc :
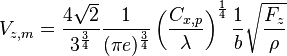
Le rapport entre la vitesse de chute minimale et la vitesse de chute à finesse maximale est :
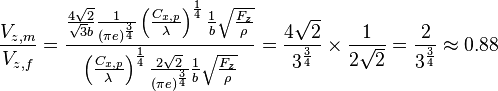
On constate donc que la vitesse de chute minimale n'est que 12 % inférieure à la vitesse de chute à finesse maximale.
Application au planeur ASW 27
On considère le planeur Alexander Schleicher ASW 27[5].
Le constructeur affirme que son planeur a une finesse de 48. Les chiffres officiels sont les suivants :
- λ = 25
- e = 0.85
- b = 15 m
- Cx,p = 0.0072 (ajusté pour satisfaire la finesse déclarée)
On obtient alors :
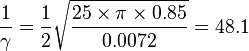
La masse à vide du planeur est 245 kg. On considère un pilote de masse 65 kg volant aux conditions normales de température et de pression. On a alors
- ρ = 1.225
- m = 310 kg
La vitesse à laquelle la finesse maximale est atteinte est
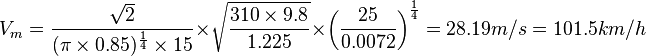
Le constructeur affirme que la finesse maximale est atteinte à 100 km/h ce qui fait que le modèle n'engendre une erreur que de moins de 2 %.
Donc, la vitesse horizontale de chute minimale sera
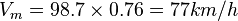
En examinant la polaire des vitesses, on constate que la vitesse de chute minimum est à 77 km/h ce qui correspond donc à la formule ci-dessus.
Le taux de chute minimal est
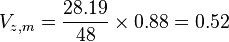
Le constructeur affirme que le taux de chute minimal est 0,52 m/s.
On constate que dans le cas du planeur ASW-27, la théorie des profils minces peut représenter la polaire des vitesses et les caractéristiques du planeur à moins de 2% près.
La finesse dans d'autres domaines
La notion de finesse s'applique aussi à d'autres domaines de la dynamique des fluides.
Voile
Une voile est aussi un profil. La notion de finesse s'applique donc aussi à ce profil, mais de plusieurs façons. Pour approfondir voir : finesse d'une voile de bateau.
Hélice de navire
Une hélice est composée de plusieurs pales. Chaque pale à un profil. La définition de finesse est identique à la finesse aérodynamique, le fluide ici étant de l'eau.
Articles connexes
- Effort sur une voile
Références
- ↑ http://para2000.org/wings/index.html
- ↑ Cumulus Soaring Polar Data
- ↑ AWS28-18 polars
- ↑ « 1er Avion à Propulsion Humaine Français en compétition Internationale » (consulté le 20 février 2015)
- ↑ (en) « ASW 27 B »
Notes
- ↑ Par la composante en x de la portance, légèrement tournée vers l'avant. La gravité n'est pas le propulseur, c'est le moteur.
- ↑ Lorsque les ascendances (mouvements verticaux ascendants de l'air environnant) sont moins fortes
- Portail de l’aéronautique