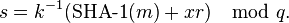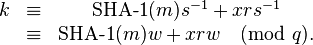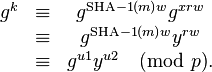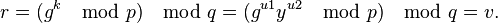Digital Signature Algorithm

Le Digital Signature Algorithm, plus connu sous le sigle DSA, est un algorithme de signature numérique standardisé par le NIST aux États-Unis, du temps où le RSA était encore breveté. Cet algorithme fait partie de la spécification DSS pour Digital Signature Standard adoptée en 1993 (FIPS 186). Une révision mineure a été publiée en 1996 (FIPS 186-1) et le standard a été amélioré en 2002 dans FIPS 186-2. Il est couvert par le brevet n° 5 231 668 aux USA (26 juin 1991) attribué à David Kravitz, ancien employé de la NSA, et il peut être utilisé gratuitement.

Aperçu

Le DSA est similaire à un autre type de signature développée par Claus-Peter Schnorr (en) en 1989. Il a aussi des points communs avec la signature ElGamal. Le processus se fait en trois étapes :

génération des clés
signature du document
vérification du document signé

Générations des clés

Leur sécurité repose sur la difficulté du problème du logarithme discret dans un groupe fini.

Choisir un nombre premier p de longueur L tel que 512 ≤ L ≤ 1024, et L est divisible par 64
Choisir un nombre premier q de 160 bits, de telle façon que p − 1 = qz, avec z un entier
Choisir h, avec 1 < h < p − 1 de manière que g = h^z mod p > 1
Générer aléatoirement un x, avec 0 < x < q
Calculer y = g^x mod p
La clé publique est (p, q, g, y). La clé privée est x

Signature

Choisir un nombre aléatoire s, 1 < s < q
Calculer s1 = (g^s mod p) mod q
Calculer s2 = (H(m) + s1*x)s^-1 mod q, où H(m) est le résultat d'un hachage cryptographique, par exemple avec SHA-1, sur le message m
La signature est (s1,s2)

Vérification

Rejeter la signature si 0<s1<q ou 0<s2<q n'est pas vérifié
Calculer w = (s2)^-1 (mod q)
Calculer u1 = H(m)*w (mod q)
Calculer u2 = s1*w (mod q)
Calculer v = [g^u1*y^u2 mod p] mod q
La signature est valide si v = s1

Validité de l'algorithme

Ce principe de signature est correct dans le sens où le vérificateur acceptera toujours des signatures authentiques. Ceci peut être démontré comme suit avec un exemple pratique :

À partir de g = h^z mod p découle :

g^q ≡ h^qz ≡ h^p-1 ≡ 1 (mod p) selon le petit théorème de Fermat. Puisque g>1 et q est premier, il s'ensuit que g a un ordre égal à q.

Celui qui procède à la signature effectue par exemple ceci (avec SHA-1) :

s=k^{-1}(\mbox{SHA-1}(m)+xr) \mod{q}.

Ainsi

\begin{matrix} k & \equiv & \mbox{SHA-1}(m)s^{-1}+xrs^{-1}\\ & \equiv & \mbox{SHA-1}(m)w + xrw \pmod{q}.\\ \end{matrix}

Comme g a un ordre q, on a :

\begin{matrix} g^k & \equiv & g^{{\rm SHA-1}(m)w}g^{xrw}\\ & \equiv & g^{{\rm SHA-1}(m)w}y^{rw}\\ & \equiv & g^{u1}y^{u2} \pmod{p}.\\ \end{matrix}

Finalement, on aboutit à la validité de DSA :

r=(g^k \mod p) \mod q = (g^{u1}y^{u2} \mod p) \mod q = v.

Voir aussi

Rivest Shamir Adleman
Signature numérique
Cryptographie asymétrique
Elliptic curve digital signature algorithm

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Digital Signature Algorithm » (voir la liste des auteurs).

Portail de la cryptologie

This article is issued from Wikipédia - version of the Wednesday, February 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.