Cryptosystème de ElGamal

Cet article est une ébauche concernant la cryptologie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Le cryptosystème d'ElGamal, ou chiffrement El Gamal (ou encore système d'El Gamal…) est un algorithme de cryptographie asymétrique fondé sur le problème du logarithme discret. Il a été créé par Taher Elgamal. Cet algorithme est utilisé par le logiciel libre GNU Privacy Guard, de récentes versions de PGP, et d'autres systèmes de chiffrement, et n'a jamais été sous la protection d'un brevet contrairement à RSA. Il peut être utilisé pour le chiffrement, mais aussi la signature électronique, par exemple l'algorithme DSA du NIST.

L'algorithme est décrit pour un groupe multiplicatif ℤ_p^*, p premier, mais n'importe quel groupe cyclique fini pour lequel le problème du logarithme discret est difficile, convient. On suppose que Bob veut envoyer un message à Alice (le chiffrement est asymétrique).

• Alice calcule deux clés, une clé publique et une clé privée : elle choisit d'abord p suffisamment grand pour que le calcul du logarithme discret soit infaisable pratiquement dans le groupe multiplicatif ℤ_p^*, g un générateur de ce groupe et un entier naturel s, s < p, puis calcule h = g^s mod p. L'entier s est la clé secrète, le triplet (p, g, h) la clé publique. Cette dernière seule est connue de Bob.
• Le message clair de Bob est supposé être m dans ℤ_p^*. Bob choisit aléatoirement un nombre entier k puis calcule (dans ℤ_p^*) c₁ = g^k et c₂ = mh^k. Le message chiffré est le couple (c₁,c₂) que Bob envoie à Alice.
• Alice peut déchiffrer le message reçu en calculant m = c₂ / c₁^s. En effet :

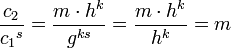
Casser l'algorithme ElGamal est dans la plupart des cas au moins aussi difficile que de calculer le logarithme discret. Cependant, il est possible qu'il existe des moyens de casser l'algorithme sans résoudre le problème du logarithme discret.

• Portail de la cryptologie