Groupe cyclique

En mathématiques et plus précisément en théorie des groupes, un groupe cyclique, ou ce qui est équivalent^[1], un groupe monogène, est un groupe dans lequel il existe un élément a tel que tout élément du groupe puisse (en notation additive) s'exprimer sous forme d'un multiple de a ; cet élément a est appelé générateur du groupe.

Il n'existe, à isomorphisme près, qu'un seul groupe cyclique infini : le groupe additif ℤ des entiers relatifs et, pour tout entier n > 0, qu'un seul groupe cyclique d'ordre n : le groupe quotient ℤ/nℤ — également noté ℤ_n ou C_n — de ℤ par le sous-groupe des multiples de n.

Les groupes cycliques sont importants en algèbre. On les retrouve, par exemple, en théorie des anneaux et en théorie de Galois.

Définitions

Un groupe cyclique est un groupe monogène, i.e. engendré par un singleton^[1]. L'expression cycle pour désigner un groupe cyclique est aussi utilisée, mais comporte un risque de confusion avec la notion de permutation circulaire.
Soit G un groupe et a un élément de G, alors le sous-groupe engendré par a est noté 〈a〉 (c'est le plus petit sous-groupe de G contenant a ; par exemple, le sous-groupe de (ℤ, +) engendré par 4 est constitué des multiples de 4).
L'ordre d'un élément a d'un groupe est l'ordre du sous-groupe 〈a〉. Cet ordre est noté |a| ou o(a). Lorsqu'il est fini, on montre que c'est le plus petit entier n strictement positif tel que :
- na = 0 (en notation additive),
- aⁿ = 1 (en notation multiplicative).
Un élément primitif^[2] d'un groupe cyclique est un élément générateur.

Applications

Théorie des groupes

Les groupes cycliques sont importants pour l'étude des groupes abéliens de type fini : tous sont des produits directs de groupes cycliques (dont certains peuvent être cycliques infinis c'est-à-dire isomorphes à ℤ). En particulier, les groupes abéliens finis sont classifiés par le théorème de Kronecker. Dans le cas des groupes finis non abéliens, le théorème de Cauchy montre l'existence de nombreux sous-groupes cycliques. Ce théorème est utilisé pour la classification des groupes finis, même si souvent, certaines formes plus élaborées sont utilisées comme les trois théorèmes de Sylow.

Arithmétique

Article détaillé : arithmétique modulaire.

En arithmétique ces groupes offrent un large répertoire d'outils et permettent de nombreuses démonstrations. Ces outils sont regroupés dans une branche des mathématiques nommée arithmétique modulaire. Ils se fondent sur l'étude des congruences sur l'anneau des entiers. On peut citer comme exemple le petit théorème de Fermat ou encore le théorème des deux carrés de Fermat avec la démonstration de Richard Dedekind. On peut encore citer la loi de réciprocité quadratique qui repose sur des structures de groupes cycliques. Il existe de nombreux cas où le groupe sous-jacent est non cyclique, mais seulement abélien de type fini, ce qui s'y ramène par produit. On le trouve par exemple dans le théorème de la progression arithmétique ou le théorème des unités de Dirichlet.

Théorie des anneaux

Les groupes cycliques jouent un rôle dans la théorie des anneaux particulièrement dans le cas des anneaux unitaires. En effet, l'unité de l'anneau engendre (pour l'addition) un groupe cyclique, permettant de définir la caractéristique d'un anneau.

Théorie de Galois

Dans le cas particulier des corps commutatifs, les groupes cycliques ont aussi un rôle fondamental. Une telle structure possède un groupe associé nommé groupe de Galois. Le théorème d'Abel-Ruffini indique que les propriétés de commutativité sont essentielles pour comprendre la théorie des équations. Le théorème de Kronecker-Weber montre que la compréhension de la résolution des équations algébriques est essentiellement liée à la structure des extensions cyclotomiques dont le groupe de Galois est cyclique.

La théorie de Galois permet aussi de construire tous les corps finis, intimement associés à la structure de groupes cycliques. Ainsi le groupe additif est un produit direct de plusieurs occurrences d'un groupe cyclique et le groupe multiplicatif est cyclique.

Théorie de l'information

La théorie de l'information utilise largement les groupes cycliques. Un élément essentiel de la cryptologie se fonde sur le fait qu'il est relativement simple de construire un grand nombre premier mais difficile de décomposer un grand nombre en nombres premiers. Ce principe est à la base du Code à clé publique RSA. Les algorithmes de décomposition, nommés test de primalité se fondent très généralement sur les groupes cycliques. On peut citer comme exemple ceux de Fermat de Miller-Rabin ou encore de Solovay-Strassen

La théorie des codes correcteurs, visant à assurer non pas la sécurité mais la fiabilité, n'est pas en reste. La grande majorité des codes utilisés dans l'industrie font partie de la famille des codes cycliques s'appuyant sur divers groupes cycliques.

Théorème fondamental

Les groupes cycliques possèdent une structure simple à comprendre. Ils forment une structure telle que les puissances d'un élément (en notation multiplicative), bien choisi, engendrent tout le groupe. Cette situation est illustrée dans la figure suivante, qui présentent les racines complexes de l'unité sur un cercle.

L'élément neutre est représenté par un point noir, un élément générateur peut être obtenu en prenant (par exemple) le premier élément en tournant vers la droite, le carré de cet élément générateur s'obtient en tournant toujours dans la même direction. Et ainsi de suite. Le (n+1)-ième élément est égal au premier, le (n+2)-ième au 2^e, et ainsi de suite.

C_n désigne le groupe cyclique d'ordre n.


C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈

La traduction en termes mathématiques est alors la suivante :

Tout groupe cyclique d'ordre n est isomorphe à ℤ/nℤ.

Ce théorème montre que ce groupe est unique pour un ordre donné et élucide complètement sa structure. Quelques corollaires en découlent immédiatement :

Tout groupe cyclique est abélien.
Soit G un groupe cyclique d'ordre n. Pour tout diviseur positif d de n, il n'existe qu'un seul sous-groupe H d'ordre d et, si g est un générateur de G, alors g^n/d est un générateur de H (qui est par conséquent cyclique).
Le quotient d'un groupe cyclique par un sous-groupe quelconque est un groupe cyclique.
Soit p un nombre premier : le groupe cyclique d'ordre p est le seul groupe d'ordre p, à isomorphisme près.

Démonstrations

Soit G un groupe cyclique d'ordre n, alors G est isomorphe à ℤ/nℤ.

Soit g un générateur de G. Les puissances de g forment un ensemble fini, si bien que g est d'ordre fini m. Le groupe G est alors constitué des m éléments distincts g⁰ = e, g¹ = g, g², … , g^m–1, donc m = n. Enfin, l'application de ℤ/nℤ dans G qui à la classe modulo n d'un entier k associe g^k est bien définie (si deux entiers représentent la même classe, les puissances correspondantes de g sont égales), et c'est clairement un isomorphisme de (ℤ/nℤ,+) dans (G,•).

Tout groupe cyclique est abélien.

En effet, la commutativité est préservée par isomorphismes, or ℤ/nℤ est abélien.

Soit G un groupe cyclique d'ordre n. Pour tout diviseur positif d de n, il n'existe qu'un seul sous-groupe H d'ordre d et, si g est un générateur de G, alors g^n/d est un générateur de H.

Soient q l'entier n/d, et g un générateur de G. Le groupe G est donc constitué des n éléments distincts g⁰ = 1, g¹ = g, g², … , g^n–1. Si l'un de ces éléments, g^r, appartient à un sous-groupe d'ordre d de G, alors d'après le théorème de Lagrange, g^rd = 1. On en déduit que rd est un multiple de n et, donc, r est un multiple de q, i.e. (puisque 0 ≤ r < n) r est l'une des valeurs 0, q, 2q, …, (d–1)q. Il n'existe donc dans G que d candidats à être éléments d'un sous-groupe d'ordre d. Il existe donc au plus un sous-groupe d'ordre d dans G : le sous-ensemble {1,g^q, g^2q, … , g^(d–1)q}. Enfin, ce sous-ensemble est bien un sous-groupe, car c'est le sous-groupe engendré par g^q. Il existe donc bien un unique sous-groupe à d éléments, ce qui termine la démonstration.

Le quotient d'un groupe cyclique par un sous-groupe quelconque est un groupe cyclique.

Les puissances d'un générateur du groupe parcourent l'intégralité du groupe, par passage au quotient, la classe du générateur engendre le groupe quotient.

Soit G un groupe d'ordre p premier, alors G est cyclique.

Soit g un élément de G différent du neutre, alors l'ordre de g est strictement supérieur à 1 et par le théorème de Lagrange, c'est un diviseur de p. Comme p est premier, l'ordre de g est donc égal à p. Le sous-groupe engendré par g est donc le groupe entier. Ce dernier est donc monogène, c'est-à-dire cyclique.

Propriétés

Théorème chinois

Article détaillé : théorème des restes chinois.

Le théorème des restes chinois permet la décomposition d'un groupe cyclique fini en groupes cycliques plus petits et, en général, plus simples. Ce théorème est largement utilisé en théorie algébrique des nombres et plus spécifiquement en arithmétique modulaire. Il est aussi à la base de nombreux algorithmes de cryptographie, on peut citer par exemple celui qui est utilisé dans le cryptage RSA. En théorie des groupes, le théorème s'énonce de la manière suivante :

Soient u et v deux entiers premiers entre eux, alors le groupe cyclique d'ordre uv est isomorphe au produit des groupes cycliques d'ordres u et v.

Note : Si u et v ne sont pas premiers entre eux, alors le groupe produit ne contient pas d'élément d'ordre supérieur au PPCM de u et de v. Ce groupe n'est donc pas isomorphe au groupe cyclique d'ordre uv.

Ce théorème entraine une décomposition unique d'un groupe cyclique en facteurs premiers ; si n est l'ordre du groupe alors le théorème fondamental de l'arithmétique montre que n se décompose de la manière unique suivante :

n = \prod_{i=1}^k p_i^{\alpha_i},

où (p_i) est une famille de k nombres premiers tous distincts et α_i des entiers supérieurs ou égaux à 1. Les puissances des nombres premiers du produit sont des nombres tous premiers entre eux. Une simple récurrence montre :

Tout groupe cyclique se décompose de manière unique en un produit de groupes cycliques d'ordre une puissance d'un nombre premier.

Démonstrations

Montrons que si u et v sont premiers entre eux, alors les groupes sont isomorphes.

D'après le #Théorème fondamental, il suffit de montrer que si u et v sont premiers entre eux, alors ℤ/(uv)ℤ est isomorphe à (ℤ/uℤ)×(ℤ/vℤ).
Soit φ_u l'application de ℤ/(uv)ℤ dans ℤ/uℤ qui à la classe modulo uv d'un entier associe la classe modulo u du même entier (on vérifie que cette définition est non ambigüe), et soit φ_v, de ℤ/(uv)ℤ dans ℤ/vℤ, définie de façon analogue. Alors φ_u et φ_v sont des morphismes, donc l'application φ de ℤ/(uv)ℤ dans (ℤ/uℤ)×(ℤ/vℤ) définie par :

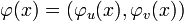
\varphi(x)=(\varphi_u(x),\varphi_v(x))

aussi.
Enfin, φ est bijective : En effet, si la classe de k (modulo uv) est élément du noyau, alors k est un multiple de u et de v. Comme ces deux nombres sont premiers entre eux, on en déduit que k est un multiple de u.v donc sa classe est nulle, et φ est injective car son noyau est réduit à l'élément neutre. Comme les groupes de départ et d'arrivée ont le même cardinal et que l'application est injective, elle est aussi surjective. Nous avons montré que φ est bijective. C'est donc un isomorphisme.

Montrons que si u et v ne sont pas premiers entre eux, alors le groupe produit ne contient pas d'élément d'ordre supérieur au PPCM de u et de v.
Notons m le PPCM de u et de v et raisonnons, comme ci-dessus, sur (ℤ/uℤ)×(ℤ/vℤ). Pour tout couple (j,k) de ce produit, m(j,k) = (mj,mk) = (0,0). On en conclut que le groupe produit ne contient pas d'élément d'ordre supérieur à m.

Indicatrice d'Euler

Article détaillé : indicatrice d'Euler.

Dans le groupe cyclique (ℤ/nℤ,+), si l'on note ses éléments 0, 1, 2,..., n – 1, alors les générateurs sont les k qui sont premiers avec n (cette propriété est démontrée dans l'article Anneau ℤ/nℤ).

Or par définition φ(n) est justement le nombre d'entiers strictement positifs inférieurs ou égaux à n et premiers avec n.

Par conséquent, le nombre de générateurs de ℤ/nℤ (donc de tout groupe cyclique d'ordre n)^[3] est égal à φ(n). Cette caractérisation de l'indicatrice d'Euler φ permet de démontrer sa multiplicativité et d'en déduire une formule explicite (voir l'article détaillé).

Du rapide inventaire ci-dessus des sous-groupes d'un groupe cyclique d'ordre n on déduit :

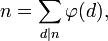
n=\sum_{d|n}\varphi(d),

équation qui fournit en retour une réciproque^[4] :

Pour qu'un groupe G d'ordre n soit cyclique, il suffit que pour tout diviseur d de n, G possède au plus un sous-groupe cyclique d'ordre d.

Ceci permet de montrer que tout sous-groupe fini du groupe multiplicatif d'un corps commutatif est cyclique^[4].

Démonstrations

Soit G un groupe d'ordre n. Pour chaque diviseur d de n, notons c(d) le nombre de sous-groupes cycliques de G d'ordre d. Le nombre d'éléments d'ordre d dans G est alors c(d)×φ(d), et n est la somme de tous ces produits.

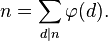
Pour G=ℤ/nℤ on a c(d)=1, d'où l'équation : $n=\sum_{d|n}\varphi(d).$
Si G est tel que chaque c(d) vaut 0 ou 1, on en déduit alors : $n=\sum_{d|n}c(d)\varphi(d)\le\sum_{d|n}\varphi(d)=n,$ si bien que tous les c(d) valent 1, en particulier c(n)=1, donc G est cyclique.
Si G est un sous-groupe du groupe multiplicatif K* d'un corps commutatif K alors chaque c(d) vaut au plus 1 (donc G est cyclique d'après ce qui précède). En effet, le polynôme X^d–1 ne peut avoir plus de d racines dans K.

Morphisme

Endomorphisme

Soit G un groupe cyclique d'ordre n, g un générateur et ψ un endomorphisme de G. La structure de G est entièrement déterminée par l'élément g. En conséquence, ψ est entièrement déterminé par l'image de g.

Réciproquement, si h est un élément de G, de la forme h = g^p avec 0 ≤ p < n, alors l'application ψ qui à x associe x^p envoie g sur h, et c'est un endomorphisme puisque

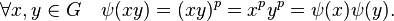
\forall x,y\in G\quad \psi(xy)=(xy)^p=x^py^p=\psi(x)\psi(y).

On en déduit les premières propriétés sur les endomorphismes des groupes cycliques :

Un endomorphisme sur un groupe cyclique est entièrement déterminé par l'image d'un générateur.

Il existe exactement n endomorphismes sur un groupe cyclique d'ordre n.

Parmi ces endomorphismes de G, ceux qui sont des automorphismes sont ceux qui envoient le générateur g sur un générateur de G. Par conséquent :

Il existe exactement φ(n) automorphismes d'un groupe cyclique d'ordre n, si φ désigne l'indicatrice d'Euler.

Ces automorphismes forment un groupe abélien fini, dont la structure est décrite dans l'article Anneau ℤ/nℤ, § Groupe des unités.

Caractère

Article détaillé : caractère d'un groupe fini.

Un caractère est un morphisme d'un groupe dans le groupe multiplicatif (ℂ*, ×) des éléments non nuls du corps des nombres complexes. Cette notion est au cœur d'une théorie importante, celle des représentations d'un groupe fini.

Il existe exactement n caractères pour un groupe cyclique d'ordre n.

L'image d'un caractère est l'ensemble des racines p-ièmes de l'unité, où p est le cardinal de l'image.

On remarquera qu'alors, p divise n.

En conséquence, tout caractère a pour image un groupe, sous-groupe de l'ensemble des racines n-ièmes de l'unité, où n est le cardinal du groupe. De plus, l'ensemble des racines n-ièmes de l'unité forme un groupe cyclique.

Soient g un générateur du groupe cyclique et r une racine n-ième de l'unité, alors il existe un et un seul caractère ψ tel que ψ(g) = r.

Ce caractère ψ est défini par :

\forall m\in\Z\quad \psi(g^m)=r^m.

Démonstrations

Soit g un générateur du groupe cyclique et r une racine n-ième de l'unité, alors il existe un et un seul caractère ψ tel que ψ(g) = r.
L'image d'un générateur détermine entièrement le caractère. Tout élément du groupe est de la forme g^m pour un certain entier m. De plus, l'application ψ définie par ψ(g^m) = r^m est clairement un morphisme.
Il existe exactement n caractères pour un groupe cyclique d'ordre n.
C'est une conséquence directe de la proposition précédente.
L'image d'un caractère est l'ensemble des racines p-ièmes de l'unité, où p est le cardinal de l'image.
L'image d'un générateur par un caractère engendre un sous-groupe, soit p son cardinal. Le théorème de Lagrange démontre que tout élément de l'image est une racine p-ième de l'unité et que p divise n. Or, il existe exactement p racines de l'unité ; ces racines forment donc l'image du caractère.

Groupes virtuellement cycliques

Un groupe G est dit virtuellement cyclique s'il possède un sous-groupe cyclique C d'indice fini (la finitude de l'indice équivaut à l'existence d'une partie finie F de G telle que tout élément de G soit le produit d'un élément de F par un élément de C).

Trivialement, tous les groupes finis sont virtuellement cycliques, ainsi que le groupe infini ℤ puisqu'il est cyclique.

Tout sous-groupe abélien d'un groupe hyperbolique est virtuellement cyclique.

Pour un groupe de type fini, le nombre de bouts (en) (du graphe de Cayley, pour n'importe quelle partie génératrice finie) est égal à 2 si et seulement si le groupe est « virtuellement cyclique infini », c'est-à-dire possède un sous-groupe d'indice fini isomorphe à ℤ.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cyclic group » (voir la liste des auteurs).

1 2 Un groupe cyclique n'est donc pas nécessairement fini, cf. Roger Godement, Cours d'algèbre, Hermann, 3^e éd., 1978, p. 121, N. Bourbaki, Groupes et algèbres de Lie, Partie 2, Springer, 2006, p. 82, et David A. Madore, « Groupe cyclique et entier modulaire ». Toutefois, N. Bourbaki, Algèbre, vol. I, Paris, 1970, p. I.47, définit un groupe cyclique comme un groupe monogène fini (le terme cyclique fait référence à une boucle : élevé à une certaine puissance n, le générateur g est égal à lui même et l'ordre du groupe est fini).
↑ (en) Christof Paar et Jan Pelzl, Understanding Cryptography, Springer,‎ 2010 (ISBN 9783642041013, lire en ligne), p. 212.
↑ Ce nombre intervient par exemple dans l'étude des polynômes cyclotomiques ou de la fonction zêta de Riemann.
1 2 (en) Joseph J. Rotman, Galois theory, Birkhäuser,‎ 1998, 2^e éd. (ISBN 978-0-38798541-1, lire en ligne), p. 64-65.

Voir aussi

Bibliographie

Serge Lang, Algèbre [détail des éditions]
J.-F. Labarre, La théorie des groupes, PUF, coll. « sciences » (n^o 1),‎ 1978 (ISBN 978-2-13035684-4)

Article connexe

Logarithme discret

Portail de l’algèbre

This article is issued from Wikipédia - version of the Wednesday, September 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Groupe cyclique

Définitions

Applications

Théorie des groupes

Arithmétique

Théorie des anneaux

Théorie de Galois

Théorie de l'information

Théorème fondamental

Propriétés

Théorème chinois

Indicatrice d'Euler

Morphisme

Endomorphisme

Caractère

Groupes virtuellement cycliques

Notes et références

Voir aussi

Bibliographie

Article connexe

Medical Encyclopedia