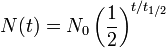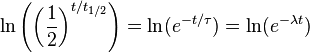Demi-vie

Sujets connexes: Physique

Contexte des ??coles Wikip??dia

Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.

Nombre de Les demi-vies pass??	Fraction restant	Pourcentage restant
0	_^1/1	100
1	_^2.1	50
2	_^1/4	25
3	_^1/8	12	0,5
4	_^16/1	6	0,25
5	_^1/32	3	0,125
6	_^1/64	1	0,563
7	_^1/128	0	0,781
...	...	...
n	_{^{2.1 N}}	100 / (2 ⁿ⁾

La demi-vie (t _??) est le temps n??cessaire pour une quantit?? de tomber ?? la moiti?? de sa valeur mesur??e au d??but de la p??riode de temps. En physique, il est g??n??ralement utilis?? pour d??crire une propri??t?? de la d??sint??gration radioactive, mais peut ??tre utilis?? pour d??crire ne importe quelle quantit?? qui va suivre d'un d??croissance exponentielle.

Le terme original, datant de Ernest Rutherford d??couverte de l 'du principe en 1907, ??tait "demi-vie", qui a ??t?? raccourci ?? "demi-vie" dans les ann??es 1950.

La demi-vie est utilis?? pour d??crire une quantit?? de subir une d??gradation exponentielle et est constante sur la dur??e de vie de la quantit?? de d??composition. C'est un unit?? caract??ristique de l'??quation de d??croissance exponentielle. Le terme "demi-vie" peut ??tre g??n??rique utilis?? pour d??signer une p??riode de temps dans laquelle une quantit?? diminue de moiti??, m??me si la carie ne est pas exponentielle. Pour une introduction g??n??rale et la description de d??croissance exponentielle, voir d??croissance exponentielle. Pour une introduction g??n??rale et une description de la carie non exponentielle, voir loi de vitesse.

L'inverse de la demi-vie est temps de doublement.

Le tableau de droite montre la r??duction d'une quantit?? en termes de nombre de demi-vies ??coul??es.

Nature probabiliste de la demi-vie

Simulation de nombreux atomes identiques subissant la d??croissance radioactive, en commen??ant par soit 4 atomes par bo??te (?? gauche) ou 400 (droite). Le nombre en haut est le nombre de demi-vies se sont ??coul??s. Notez le loi des grands nombres: Avec plusieurs atomes, la d??croissance globale est plus r??guli??re et plus pr??visible.

Une demi-vie d??crit habituellement le d??clin des entit??s discr??tes, tels que des atomes radioactifs, qui ont des noyaux instables. Dans ce cas, il ne fonctionne pas ?? utiliser la d??finition de ??demi-vie est le temps n??cessaire pour exactement la moiti?? des entit??s de la corruption??. Par exemple, se il n'y a qu'un seul atome radioactif avec une demi-vie de une seconde, il n'y aura pas "une moiti?? d'un atome" gauche apr??s une seconde. Il y aura soit z??ro atomes gauche ou une gauche atome, selon si oui ou non cet atome qui se est pass?? ?? la pourriture.

Au lieu de cela, la demi-vie est d??finie en termes de probabilit?? . Ce est le moment o?? le valeur attendue du nombre d'entit??s qui ont cari??es est ??gal ?? la moiti?? du nombre d'origine. Par exemple, on peut commencer avec un seul atome radioactif, attendez sa demi-vie, et puis v??rifier si oui ou non il se est d??sint??gr??. Peut-??tre qu'il a fait, mais peut-??tre qu'il n'a pas fait. Mais si cette exp??rience est r??p??t??e ?? plusieurs reprises, on voit que - en moyenne - il se d??sint??gre ?? l'int??rieur de la demi-vie de 50% du temps.

Dans certaines exp??riences (comme la synth??se d'un ??l??ment super-lourd), il est en fait un seul atome radioactif produit ?? la fois, avec sa dur??e de vie mesur??e individuellement. Dans ce cas, l'analyse statistique est n??cessaire de d??duire la demi-vie. Dans d'autres cas, un tr??s grand nombre d'atomes radioactifs identiques d??croissance dans la plage de temps mesur??. Dans ce cas, la loi des grands nombres se assure que le nombre d'atomes qui en fait la d??composition est approximativement ??gal au nombre d'atomes qui sont attendus ?? la pourriture. En d'autres termes, avec un assez grand nombre d'atomes en d??composition, les aspects probabilistes du processus pourraient ??tre n??glig??s.

Il ya divers exercices simples qui d??montrent d??croissance probabiliste, par exemple impliquant retournement des pi??ces de monnaie ou de diriger une statistique Programme d'ordinateur. Par exemple, l'image sur la droite est une simulation de nombreux atomes identiques subissant la d??croissance radioactive. Notez que, apr??s une demi-vie, il ne est pas exactement la moiti?? des atomes restants, seulement environ, en raison de la variation al??atoire dans le processus. Cependant, avec plusieurs atomes (bo??tes ?? droite), la d??croissance globale est plus lisse et moins al??atoire prospectifs qu'avec moins d'atomes (bo??tes ?? gauche), conform??ment ?? la loi des grands nombres.

Formules pour la demi-vie en d??croissance exponentielle

Un processus de d??croissance exponentielle peut ??tre d??crit par l'une des trois formules ??quivalentes suivantes:

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = N_0 e ^ {- t / \ tau} \,$

$N (t) = N_0 e ^ {- \ lambda t} \,$

o??

N ₀ est la quantit?? initiale de la substance qui va se d??grader (cette quantit?? peut ??tre mesur??e en grammes moles, le nombre d'atomes de carbone, etc.),
N (t) est la quantit?? qui reste immobile et ne est pas encore d??compos??s apr??s un temps t,
t _1/2 est la demi-vie de la quantit?? de d??composition,
τ est un nombre positif appel?? dur??e de vie de la quantit?? de d??composition signifie,
λ est un nombre positif appel?? constante de d??sint??gration de la quantit?? de d??composition.

Les trois param??tres 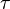$t_ {1/2}$ , $\ Tau$ Et λ sont tous directement li??s de la mani??re suivante:

$t_ {1/2} = \ frac {\ ln (2)} {\ lambda} = \ tau \ ln (2)$

o?? ln (2) est le logarithme naturel de 2 (environ 0,693).

Cliquez sur "show" de voir un calcul d??taill?? de la relation entre la demi-vie, temps de d??croissance, et constante de d??sint??gration.

Commencez par les trois ??quations

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = N_0 e ^ {- t / \ tau}$

$N (t) = N_0 e ^ {- \ lambda t}$

Nous voulons trouver une relation entre 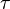$t_ {1/2}$ , $\ Tau$ Et λ, de telle sorte que ces trois ??quations d??crivent exactement le m??me processus de d??croissance exponentielle. En comparant les ??quations, nous trouvons la condition suivante:

$\ Left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = e ^ {- t / \ tau} = e ^ {- \ lambda t}$

Ensuite, nous prendrons le logarithme naturel de chacun de ces quantit??s.

$\ En \ left (\ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} \ right) = \ ln (e ^ {- t / \ tau}) = \ ln (e ^ {- \ lambda t})$

En utilisant les propri??t??s des logarithmes, ce qui simplifie de ce qui suit:

$(T / t_ {1/2}) \ En \ left (\ frac {1} {2} \ right) = (-t / \ tau) \ ln (e) = (- \ lambda t) \ ln (e )$

Depuis le logarithme naturel de e est 1, on obtient:

$(T / t_ {1/2}) \ En \ left (\ frac {1} {2} \ right) = -t / \ tau = - \ lambda t$

Annulation du facteur de t et de brancher 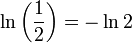$\ En \ left (\ frac {1} {2} \ right) = - \ ln 2$ , Le r??sultat final est:

$t_ {1/2} = \ tau \ ln 2 = \ frac {\ ln 2} {\ lambda}.$

En branchant et manipuler ces relations, nous obtenons toutes les descriptions ??quivalentes suivantes de d??croissance exponentielle, en termes de demi-vie:

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = N_0 2 ^ {- t / t_ {1/2}} = N_0 e ^ {-t \ ln (2) / t_ {2.1}}$

$t_ {1/2} = t / \ log_2 (N_0 / N (t)) = t / (\ log_2 (N_0) - \ log_2 (N (t))) = (\ log_ {2} ^ t (N_0 / N (t))) ^ {- 1} = T \ ln (2) / \ ln (N_0 / N (t))$

Ind??pendamment de la fa??on dont ce est ??crit, nous pouvons brancher sur la formule pour obtenir

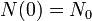$N (0) = N_0$ comme pr??vu (ce est la d??finition de ??quantit?? initiale")
$N (t_ {1/2}) = \ left (\ frac {1} {2} \ right) N_0$ comme pr??vu (ce est la d??finition de demi-vie)
$\ {Lim_ t \ to \ infty} N (t) = 0$ , Ce est ?? dire montant se rapproche de z??ro lorsque t tend vers l'infini comme pr??vu (plus nous attendons, moins les restes).

Decay par plusieurs proc??d??s

Certaines quantit??s d??croissance exponentielle par deux processus de d??sint??gration simultan??ment. Dans ce cas, la demi-vie effective T _1/2 peut ??tre li??e ?? la demi-vie t ₁ et t ₂ que la quantit?? auraient si chacun des processus de d??sint??gration a agi de fa??on isol??e:

$\ Frac {1} {{1/2} T_} = \ frac {1} {} t_1 + \ frac {1} {} t_2$

Pendant trois ou plusieurs processus, la formule est analogue:

$\ frac {1} {{T_ 1/2}} = \ frac {1} {} t_1 + \ frac {1} {} t_2 + \ frac {1} {} + \ t_3 cdots$

Pour une preuve de ces formules, voir Decay par deux ou plusieurs processus.

Exemples

Il ya une demi-vie d??crivant tout processus exponentiel d??sint??gration. Par exemple:

Le courant circulant ?? travers un Circuit RC ou Circuit RL se d??sint??gre avec une demi-vie de $RC \ ln (2)$ ou $\ Ln (2) L / R$ Respectivement. Pour cet exemple, le terme la mi-temps pourrait ??tre utilis?? ?? la place de ??demi-vie??, mais ils veulent dire la m??me chose.
Dans un premier ordre r??action chimique , la demi-vie du r??actif est $\ Ln (2) / \ lambda$ O?? λ est la vitesse de r??action constante.
En d??sint??gration radioactive, la demi-vie est la longueur de temps apr??s lequel il ya une probabilit?? de 50% qu'un atome aura subi nucl??aire d??croissance. Elle varie en fonction du type d'atome et des isotopes , et est g??n??ralement d??termin??e exp??rimentalement. Voir Liste des nucl??ides.

la demi-vie d'une esp??ce est le temps n??cessaire pour que la concentration de la substance ?? tomber ?? la moiti?? de sa valeur initiale

Demi-vie dans la carie non exponentielle

La d??croissance de nombreuses grandeurs physiques ne sont pas exemple exponentielle pour l'??vaporation de l'eau d'une flaque d'eau, ou (souvent) la r??action chimique d'une mol??cule. Dans de tels cas, la demi-vie est d??fini de la m??me mani??re que pr??c??demment: comme le temps ??coul?? avant la moiti?? de la quantit?? initiale se est d??sint??gr??e. Cependant, contrairement ?? une d??croissance exponentielle, la demi-vie d??pend de la quantit?? initiale, et la demi-vie prospective va changer au fil du temps que la quantit?? se d??sint??gre.

A titre d'exemple, la d??sint??gration radioactive de carbone-14 est exponentielle avec une demi-vie de 5730 ans. Une quantit?? de carbone-14 se d??sint??gre ?? la moiti?? de son montant initial ( sur moyenne ) apr??s 5730 ann??es, quel que soit grand ou petit la quantit?? initiale ??tait. Apr??s encore 5730 ann??es, un quart de l'original restera. D'autre part, le temps qu'il faudra une flaque d'eau ?? moiti??-??vaporer d??pend de la profondeur de la flaque d'eau est. Peut-??tre une flaque d'une certaine taille se ??vapore ?? la moiti?? de son volume initial en une journ??e. Mais le deuxi??me jour, il n'y a aucune raison de se attendre ?? ce que le quart de la flaque restera; en fait, il sera probablement beaucoup moins. Il se agit d'un exemple dans lequel la demi-vie diminue ?? mesure que le temps passe. (En d'autres d??sint??grations non exponentielles, il peut augmenter la place).

La d??sint??gration d'un m??lange de deux ou plusieurs mat??riaux qui chaque d??sint??gration exponentielle, mais avec des demi-vies, ne est pas exponentielle. Math??matiquement, la somme de deux fonctions exponentielles ne est pas une fonction exponentielle simple. Un exemple courant d'une telle situation sont les d??chets des centrales nucl??aires, qui est un m??lange de substances tr??s diff??rentes avec des demi-vies. Consid??rons un ??chantillon contenant un ??l??ment A d??composition rapide, avec une demi-vie de 1 seconde, et un ??l??ment B d??croissant lentement, avec une demi-vie d'un an. Apr??s quelques secondes, presque tous les atomes de l'??l??ment A ont d??cru apr??s division par deux r??p??t??e du nombre total initial d'atomes; mais tr??s peu des atomes de l'??l??ment B aura encore cari??es que seule une infime fraction d'un demi-vie se est ??coul??e. Ainsi, le m??lange dans son ensemble ne se d??grade pas par moiti??s.

Demi-vie dans la biologie et la pharmacologie

Un demi-vie biologique ou demi-vie d'??limination est le temps qu'il faut ?? une substance (drogue, nucl??ide radioactif ou autre) de perdre la moiti?? de sa pharmacologique, physiologique, ou d'une activit?? radiologique. Dans un contexte m??dical, la demi-vie peut ??galement d??crire le temps qu'il faut pour que la concentration en le plasma sanguin d'une substance pour atteindre la moiti?? de sa valeur en r??gime permanent (la "demi-vie plasmatique").

La relation entre les demi-vies biologiques et de plasma d'une substance peut ??tre complexe, en raison de facteurs, dont l'accumulation dans tissus, actif m??tabolites, et interactions r??cepteur.

Alors un isotope radioactif se d??sint??gre presque parfaitement selon soi-disant ??cin??tique de premier ordre??, o?? la constante de vitesse est un nombre fixe, l'??limination d'une substance par un organisme vivant suit g??n??ralement la cin??tique chimique plus complexes.

Par exemple, la demi-vie biologique de l'eau dans un ??tre humain est d'environ 7 ?? 14 jours, bien que cela puisse ??tre modifi??e par son / son comportement. La demi-vie biologique de c??sium des ??tres humains est comprise entre un et quatre mois. Cela peut ??tre raccourcie en alimentant la personne le bleu de Prusse, qui agit comme un solide ??changeur d'ions qui absorbe le c??sium tout en lib??rant de potassium ions ?? leur place.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Half-life&oldid=550971959 "