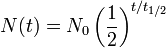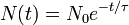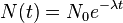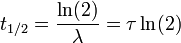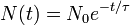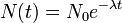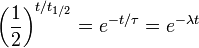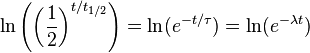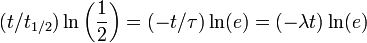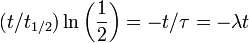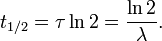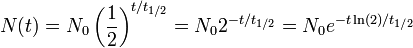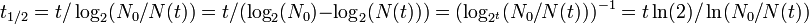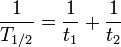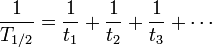Media vida

Temas relacionados: F??sica

Antecedentes de las escuelas de Wikipedia

Los art??culos de esta selecci??n escuelas se han organizado por tema curr??culo gracias a voluntarios SOS. SOS es la mayor donaci??n de caridad del mundo ni??os hu??rfanos y abandonados de la oportunidad de la vida familiar.

N??mero de vidas medias transcurrido	Fracci??n restante	Porcentaje restante
0	_^1/1	100
1	_^1/2	50
2	_^1/4	25
3	_^1/8	12	0.5
4	_^1/16	6	0.25
5	_^1/32	3	0,125
6	_^1/64	1	0,563
7	_^1/128	0	0,781
...	...	...
n	_{^{1/2 n}}	100 / (2 ⁿ⁾

La vida media (t _??) es el tiempo requerido para una cantidad a caer a la mitad de su valor como medido al comienzo del per??odo de tiempo. En f??sica, se suele utilizar para describir una propiedad de la desintegraci??n radiactiva, pero que puede utilizarse para describir cualquier cantidad que sigue una decaimiento exponencial.

El t??rmino original, que data de Ernest Rutherford descubrimiento 's del principio en 1907, fue "per??odo de vida media", que fue acortado a "vida media" a principios de 1950.

La vida media se usa para describir una cantidad de someterse decaimiento exponencial, y es constante durante la vida ??til de la cantidad de descomposici??n. Es un unidad de caracter??stica para la ecuaci??n de decaimiento exponencial. El t??rmino "semivida" gen??ricamente se puede usar para referirse a cualquier per??odo de tiempo en el que una cantidad cae a la mitad, incluso si la descomposici??n no es exponencial. Para una introducci??n general y descripci??n de decaimiento exponencial, consulte decaimiento exponencial. Para una introducci??n general y descripci??n de la decadencia no exponencial, consulte ley de velocidad.

Lo contrario de la vida media es de tiempo de duplicaci??n.

La tabla de la derecha muestra la reducci??n de una cantidad en t??rminos del n??mero de vidas medias transcurridos.

Naturaleza probabil??stica de la vida media

Simulaci??n de muchos ??tomos id??nticos someterse a la desintegraci??n radiactiva, comenzando con una extensi??n de 4 ??tomos por caja (izquierda) o 400 (derecha). El n??mero en la parte superior es c??mo han transcurrido muchas vidas medias. Tenga en cuenta la ley de los grandes n??meros: Con m??s ??tomos, el decaimiento general es m??s regular y predecible.

Una vida media suele describir la decadencia de entidades discretas, tales como ??tomos radiactivos, que tienen n??cleos inestables. En ese caso, no funciona al utilizar la definici??n de "vida media es el tiempo necesario para que exactamente la mitad de las entidades de la corrupci??n". Por ejemplo, si s??lo hay un ??tomo radiactivo con una vida media de un segundo, habr?? no ser "uno-medio de un ??tomo" izquierda despu??s de un segundo. No habr?? ya sea cero ??tomos de la izquierda o de la izquierda ??tomo, dependiendo de si o no ese ??tomo ocurri?? a las caries.

En lugar de ello, la vida media se define en t??rminos de probabilidad . Es el tiempo cuando el valor esperado del n??mero de entidades que han cariados es igual a la mitad del n??mero original. Por ejemplo, se puede comenzar con un solo ??tomo radiactivo, espera que su vida media, y luego comprobar si es o no ha deca??do. Tal vez lo hizo, pero tal vez no lo hizo. Pero si este experimento se repite una y otra vez, se ver?? que - en promedio - se descompone dentro de la vida media de 50% del tiempo.

En algunos experimentos (tales como la s??ntesis de una elemento superpesado), hay, de hecho, s??lo un ??tomo radiactivo producido en un momento, con su tiempo de vida medido individualmente. En este caso, se requiere un an??lisis estad??stico para inferir la vida media. En otros casos, un n??mero muy grande de id??ntica ??tomos radiactivos descomposici??n en el intervalo de tiempo medido. En este caso, el ley de los grandes n??meros asegura que el n??mero de ??tomos que en realidad la caries es aproximadamente igual al n??mero de ??tomos que se espera a decaer. En otras palabras, con un n??mero suficientemente grande de ??tomos en descomposici??n, los aspectos probabil??sticos del proceso podr??an ser descuidado.

Hay varios ejercicios sencillos que demuestran la decadencia probabil??stico, por ejemplo que implican mover de un tir??n monedas o de ejecutar una estad??stica programa de computadora. Por ejemplo, la imagen de la derecha es una simulaci??n de muchos ??tomos id??nticos sometidos a la desintegraci??n radiactiva. Tenga en cuenta que despu??s de una vida media no son exactamente la mitad de los ??tomos restantes, s??lo aproximadamente, debido a la variaci??n aleatoria en el proceso. Sin embargo, con m??s ??tomos (cajas a la derecha), el decaimiento general es m??s suave y menos aleatoria buscando que con un menor n??mero de ??tomos (cajas de la izquierda), de conformidad con el ley de los grandes n??meros.

F??rmulas para la vida media de decaimiento exponencial

Un proceso de decaimiento exponencial puede ser descrita por cualquiera de las tres f??rmulas equivalentes siguientes:

$N (t) = n_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = e ^ {n_0 - t / \ tau} \,$

$N (t) = e ^ {n_0 - \ lambda t} \,$

donde

N ₀ es la cantidad inicial de la sustancia que va a decaer (esta cantidad puede medirse en gramos, moles, el n??mero de ??tomos, etc.),
N (t) es la cantidad que todav??a permanece y a??n no ha deca??do despu??s de un tiempo t,
t _medio es la vida media de la cantidad de descomposici??n,
τ es una n??mero positivo llamado tiempo de vida de la cantidad de descomposici??n significar,
λ es un n??mero positivo llamado constante de desintegraci??n de la cantidad en descomposici??n.

Los tres par??metros 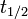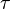$t_ {1/2}$ , $\ Tau$ Y λ est??n directamente relacionados de la siguiente manera:

$t_ {1/2} = \ frac {\ ln (2)} {\ lambda} = \ tau \ ln (2)$

donde ln (2) es el logaritmo natural de 2 (aproximadamente 0.693).

Haga clic en "indique" para ver una derivaci??n detallada de la relaci??n entre la vida media, tiempo de ca??da, y la decadencia constante.

Comience con las tres ecuaciones

$N (t) = n_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = e ^ {n_0 - t / \ tau}$

$N (t) = e ^ {n_0 - \ lambda t}$

Queremos encontrar una relaci??n entre 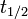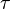$t_ {1/2}$ , $\ Tau$ Y λ, de tal manera que estas tres ecuaciones describen exactamente el mismo proceso de decaimiento exponencial. Comparando las ecuaciones, encontramos la siguiente condici??n:

$\ Left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = e ^ {- t / \ tau} = e ^ {- \ lambda t}$

A continuaci??n, vamos a tomar el logaritmo natural de cada una de estas cantidades.

$\ Ln \ left (\ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} \ right) = \ ln (e ^ {- t / \ tau}) = \ ln (e ^ {- \ lambda t})$

Uso de las propiedades de los logaritmos, esto simplifica a lo siguiente:

$(T / t_ {1/2}) \ ln \ left (\ frac {1} {2} \ right) = (-t / \ tau) \ ln (e) = (- \ lambda t) \ ln (e )$

Desde el logaritmo natural de e es 1, obtenemos:

$(T / t_ {1/2}) \ ln \ left (\ frac {1} {2} \ right) = -t / \ tau = - \ lambda t$

Cancelaci??n el factor de t y enchufar $\ Ln \ left (\ frac {1} {2} \ right) = - \ ln 2$ , El resultado final es:

$t_ {1/2} = \ tau \ ln 2 = \ frac {\ ln 2} {\ lambda}.$

Al conectar y manipular estas relaciones, obtenemos todas las siguientes descripciones equivalentes de decaimiento exponencial, en t??rminos de la vida media:

$N (t) = n_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = n_0 2 ^ {- t / t_ {1/2}} = n_0 e ^ {-t \ ln (2) / t_ {1/2}}$

$t_ {1/2} = t / \ log_2 (n_0 / N (t)) = t / (\ log_2 (n_0) - \ log_2 (N (t))) = (\ log_ {2 ^ t} (n_0 / N (t))) ^ {- 1} = T \ ln (2) / \ ln (n_0 / N (t))$

Independientemente de la forma en que est?? escrito, podemos conectar a la f??rmula para obtener

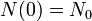$N (0) = n_0$ como se esperaba (esta es la definici??n de "cantidad inicial")
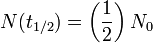$N (t_ {1/2}) = \ left (\ frac {1} {2} \ right) n_0$ como se esperaba (esta es la definici??n de un medio de vida)
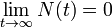$\ Lim_ {t \ to \ infty} N (t) = 0$ , Es decir, la cantidad se aproxima a cero cuando t tiende a infinito como esper??bamos (cuanto m??s esperemos, lo es menos).

Decay por dos o m??s procesos

Algunas cantidades caries por dos procesos exponencial de decaimiento simult??neamente. En este caso, el actual T media vida _media puede estar relacionado con las vidas medias t ₁ y t ₂ que la cantidad tendr??an si cada uno de los procesos de desintegraci??n actuaron de aislamiento:

$\ Frac {1} {T_ {1/2}} = \ frac {1} {t_1} + \ frac {1} {t_2}$

Durante tres o m??s procesos, la f??rmula an??loga es:

$\ frac {1} {T_ {1/2}} = \ frac {1} {t_1} + \ frac {1} {t_2} + \ frac {1} {t_3} + \ cdots$

Para una prueba de estas f??rmulas, ver Decay por dos o m??s procesos.

Ejemplos

Hay una vida media que describe cualquier proceso de desintegraci??n exponencial. Por ejemplo:

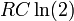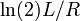La corriente que fluye a trav??s de una Circuito RC o Circuito RL se desintegra con una vida media de $RC \ ln (2)$ o $\ Ln (2) L / R$ , Respectivamente. Para este ejemplo, el t??rmino medio tiempo podr??a ser utilizado en lugar de "media vida", pero significa lo mismo.
En un primer orden reacci??n qu??mica , la vida media de la sustancia reaccionante es 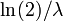$\ Ln (2) / \ lambda$ , Donde λ es la velocidad de reacci??n constante.
En desintegraci??n radiactiva, la vida media es el tiempo tras el que hay una probabilidad del 50% de que un ??tomo habr?? experimentado nuclear decadencia. Var??a en funci??n del tipo ??tomo y de is??topos , y generalmente se determina experimentalmente. Ver Lista de nucleidos.

la vida media de una especie es el tiempo que tarda la concentraci??n de la sustancia caiga a la mitad de su valor inicial

La vida media en decadencia no exponencial

La decadencia de muchas magnitudes f??sicas no es ejemplo exponencial-para, la evaporaci??n del agua de un charco, o (a menudo) la reacci??n qu??mica de una mol??cula. En tales casos, la vida media se define de la misma manera que antes: como el tiempo transcurrido antes de la mitad de la cantidad original ha deca??do. Sin embargo, a diferencia de en un decaimiento exponencial, la vida media depende de la cantidad inicial, y la vida media prospectivo cambiar?? con el tiempo como la cantidad decae.

Como ejemplo, la desintegraci??n radiactiva de carbono-14 es exponencial, con una vida media de 5.730 a??os. Una cantidad de carbono-14 decaer?? hasta la mitad de su valor original ( en promedio ) despu??s de 5.730 a??os, sin importar lo grande o peque??a que sea la cantidad original. Despu??s de otros 5730 a??os, una cuarta parte de la original permanecer??. Por otro lado, el tiempo que tomar?? un charco de medio-evaporan depende de la profundidad del charco es. Tal vez un charco de un cierto tama??o se evaporar?? hasta la mitad de su volumen original en un d??a. Pero en el segundo d??a, no hay ninguna raz??n para esperar que una cuarta parte de la charco permanecer??; de hecho, es probable que sea mucho menos que eso. Este es un ejemplo en el que la vida media se reduce a medida que pasa el tiempo. (En otras desintegraciones no exponencial, puede aumentar su lugar).

La decadencia de una mezcla de dos o m??s materiales que cada decaimiento exponencial, pero con diferentes vidas medias, no es exponencial. Matem??ticamente, la suma de dos funciones exponenciales no es una sola funci??n exponencial. Un ejemplo com??n de esta situaci??n es el de residuos de las centrales nucleares, que es una mezcla de sustancias con muy diferentes vidas medias. Considere una muestra que contiene un elemento de descomposici??n r??pidamente A, con una vida media de 1 segundo, y un elemento de descomposici??n lentamente B, con una vida media de un a??o. Despu??s de unos pocos segundos, casi todos los ??tomos del elemento A se han deteriorado despu??s de reducir a la mitad repetida del n??mero total inicial de ??tomos; pero muy pocos de los ??tomos del elemento B habr?? todav??a deca??do como ha transcurrido s??lo una peque??a fracci??n de una vida media. Por lo tanto, la mezcla tomada en su conjunto no se descompone por mitades.

La vida media en la biolog??a y farmacolog??a

La vida media biol??gica o vida media de eliminaci??n es el tiempo que toma para que una sustancia (drogas, nucleido radiactivo, u otro) para perder la mitad de su farmacol??gica, fisiol??gica, o actividad radiol??gica. En un contexto m??dico, la vida media tambi??n puede describir el tiempo que tarda la concentraci??n en plasma de la sangre de una sustancia para llegar a la mitad de su valor de estado estacionario (la "vida media plasm??tica").

La relaci??n entre las vidas medias biol??gicas y de plasma de una sustancia puede ser complejo, debido a factores como la acumulaci??n en tejidos, activa metabolitos, y interacciones receptor.

Mientras que un is??topo radiactivo se desintegra casi perfectamente de acuerdo con los llamados "cin??tica de primer orden", donde la constante de velocidad es un n??mero fijo, la eliminaci??n de una sustancia de un organismo vivo por lo general sigue la cin??tica qu??mica m??s complejos.

Por ejemplo, la vida media biol??gica de agua en un ser humano es de aproximadamente 7 a 14 d??as, aunque esto puede ser alterado por su / su comportamiento. La vida media biol??gica de cesio en los seres humanos es de entre uno y cuatro meses. Esto puede ser acortado por la alimentaci??n de la persona azul de Prusia, que act??a como un s??lido intercambiador de iones que absorbe el cesio mientras que la liberaci??n de potasio iones en su lugar.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Half-life&oldid=550971959 "