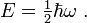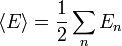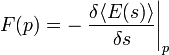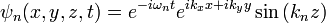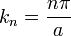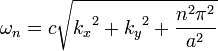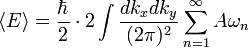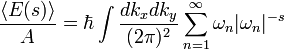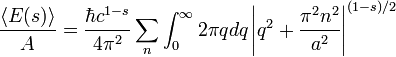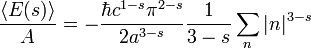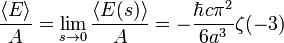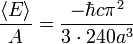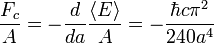Efecto Casimir

Temas relacionados: F??sica

Antecedentes

SOS Children, una organizaci??n ben??fica educaci??n , organiz?? esta selecci??n. SOS Children ha cuidado de ni??os en ??frica durante cuarenta a??os. ??Puedes ayudar a su trabajo en ??frica ?

Las fuerzas de Casimir sobre placas paralelas.

Las fuerzas de Casimir sobre placas paralelas.

En la f??sica , el efecto Casimir y la fuerza de Casimir-p??lder son f??sicos fuerzas resultantes de un campo cuantificado . El ejemplo t??pico es de dos no cargados placas met??licas en una vac??o, colocado unos pocos micr??metros de distancia, sin ning??n externa campo electromagn??tico. En un descripci??n cl??sica, la falta de un campo externo tambi??n significa que no hay ning??n campo entre las placas, y ninguna fuerza se mide entre ellos. Cuando este campo se estudi?? en lugar de utilizar la mec??nica cu??ntica , se ve que las placas no afectan a la virtuales fotones que constituyen el campo, y generar una fuerza neta, ya sea una atracci??n o una repulsi??n dependiendo de la disposici??n espec??fica de las dos placas. Esta fuerza se ha medido, y es un ejemplo llamativo de un efecto puramente debido a segunda cuantizaci??n. (Sin embargo, el tratamiento de condiciones de contorno en estos c??lculos ha dado lugar a cierta controversia.)

Holand??s los f??sicos Hendrik BG Casimir y Dirk Polder propuso por primera vez la existencia de la fuerza y formul?? un experimento para detectarla en 1948 durante su participaci??n en la investigaci??n en Philips Research Labs. La forma cl??sica del experimento, descrito anteriormente, demostr?? con ??xito a la fuerza dentro del 15% del valor predicho por la teor??a.

Debido a que la intensidad de la fuerza disminuye r??pidamente con la distancia, s??lo es medible cuando la distancia entre los objetos es extremadamente peque??o. En una escala submicrometre, esta fuerza se vuelve tan fuerte que se convierte en la fuerza dominante entre los conductores no cargados. De hecho, en separaciones de 10 nm-alrededor de 100 veces el tama??o t??pico de un ??tomo-efecto Casimir produce el equivalente a 1 atm??sfera de presi??n (101,3 kPa), el valor exacto en funci??n de la geometr??a de la superficie y otros factores .

Aunque el efecto Casimir se puede expresar en t??rminos de part??culas virtuales que interact??an con los objetos, que se describe mejor y se calcula m??s f??cilmente en t??rminos de la energ??a de punto cero de un campo cuantificada en el espacio intermedio entre los objetos. En el moderno f??sica te??rica, el efecto Casimir desempe??a un papel importante en el modelo de bolsa quiral de la nucle??n; y en F??sica Aplicada, que se est?? convirtiendo cada vez m??s importante en el desarrollo de los componentes cada vez m??s peque??os miniaturizados de emergente microtecnolog??as y nanotecnolog??as.

Visi??n de conjunto

El efecto Casimir puede ser comprendido por la idea de que la presencia de metales conductores y diel??ctricos alteran la valor esperado de vac??o de la energ??a de la segunda cuantificada campo electromagn??tico. Dado que el valor de esta energ??a depende de las formas y posiciones de los conductores y diel??ctricos, el efecto Casimir se manifiesta como una fuerza entre tales objetos.

Energ??a del vac??o

El efecto Casimir es un resultado de la teor??a cu??ntica de campos , que establece que todos los diversos fundamental campos, tales como la campo electromagn??tico, debe ser cuantificada en todas y cada punto en el espacio. En una vista simplificada, un "campo" en la f??sica puede ser concebido como si el espacio se llena de bolas vibrantes interconectados y los resortes, y la fuerza del campo puede ser visualizado como el desplazamiento de un bal??n desde su posici??n de reposo. Las vibraciones en este campo se propagan y se rigen por la adecuada ecuaci??n de onda para el campo en cuesti??n. La segunda cuantizaci??n de la teor??a cu??ntica de campos requiere que se va a cuantificar cada uno de esos combinaci??n de bola de primavera, es decir, que la fuerza del campo se va a cuantificar en cada punto en el espacio. Can??nicamente, el campo en cada punto en el espacio es una oscilador arm??nico simple, y su cuantificaci??n coloca una oscilador arm??nico cu??ntico en cada punto. Excitaciones del campo corresponden a la part??culas elementales de la f??sica de part??culas . Sin embargo, incluso la de vac??o tiene una estructura muy compleja. Todos los c??lculos de la teor??a cu??ntica de campos se deben realizar en relaci??n a este modelo de la aspiradora.

El vac??o tiene, impl??citamente, todas las propiedades que una part??cula puede tener: giro, o la polarizaci??n en el caso de la luz , la energ??a , y as?? sucesivamente. En promedio, todas estas propiedades se cancelan: el vac??o es, despu??s de todo, "vac??o" en este sentido. Una excepci??n importante es la energ??a del vac??o o de la valor esperado de vac??o de la energ??a. La cuantificaci??n de un oscilador arm??nico simple establece que la energ??a m??s bajo posible o la energ??a de punto cero que un oscilador de este tipo puede tener es

${E} = \ begin {matriz} \ frac {1} {2} \ end {matriz} \ hbar \ omega \.$

Sumando sobre todos los osciladores posibles en todos los puntos en el espacio da una cantidad infinita. Para eliminar este infinito, se puede argumentar que s??lo las diferencias en la energ??a son f??sicamente medible; este argumento es la base de la teor??a de renormalizaci??n . En todos los c??lculos pr??cticos, as?? es como el infinito siempre se maneja. En un sentido m??s profundo, sin embargo, la renormalizaci??n es poco satisfactoria, y la retirada de este infinito presenta un desaf??o en la b??squeda de un Teor??a del Todo. Actualmente no hay una explicaci??n convincente de c??mo este infinito se debe tratar como esencialmente cero; un valor distinto de cero es esencialmente el constante cosmol??gica y cualquier valor grande provoca problemas en la cosmolog??a .

El efecto Casimir

La observaci??n de Casimir fue que el campo electromagn??tico cu??ntica segundo cuantificado, en la presencia de cuerpos a granel, tales como metales o diel??ctricos, deben obedecer a la misma condiciones de contorno que el campo electromagn??tico cl??sico debe obedecer. En particular, esto afecta el c??lculo de la energ??a del vac??o en la presencia de una conductor o diel??ctrico.

Consideremos, por ejemplo, el c??lculo del valor esperado de vac??o del campo electromagn??tico dentro de una cavidad de metal, tal como, por ejemplo, una cavidad de radar o una microonda gu??a de onda. En este caso, la forma correcta de encontrar la energ??a del punto cero del campo es sumar las energ??as de la ondas de la cavidad de pie. A todos y cada onda estacionaria posible corresponde una energ??a; decir la energ??a de la n-??sima onda estacionaria es 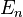$E_n$ . El valor esperado de vac??o de la energ??a del campo electromagn??tico en la cavidad es entonces

$\ Langle E \ rangle = \ frac {1} {2} \ sum_n E_n$

con la suma continua sobre todos los valores posibles de n enumeraci??n de las ondas estacionarias. El factor de media corresponde al hecho de que las energ??as de punto cero se suman (que es el mismo medio como aparece en la ecuaci??n 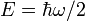$E = \ hbar \ omega / 2$ ). Escrito de esta manera, esta suma es claramente divergente; sin embargo, puede ser usado para crear expresiones finitos.

En particular, cabe preguntarse c??mo la energ??a de punto cero depende de la forma s de la cavidad. Cada nivel de energ??a 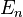$E_n$ depende de la forma, y lo que uno debe escribir 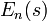$E_n (s)$ para el nivel de energ??a, y 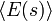$\ Langle E (s) \ rangle$ para el valor esperado de vac??o. En este punto viene una observaci??n importante: la fuerza en el punto P en la pared de la cavidad es igual al cambio en la energ??a del vac??o si la forma s de la pared se perturba un poco, por decirlo 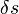$\ Delta s$ , En el punto p. Es decir, uno tiene

$F (p) = - \ left. \ Frac {\ delta \ langle E (s) \ rangle} {\ delta s} \ right \ vert_p \,$

Este valor es finito en muchos c??lculos pr??cticos.

C??lculo de Casimir

En el c??lculo original hecho por Casimir, que consideraba el espacio entre un par de placas de metal que llevan a cabo una distancia un aparte. En este caso, las ondas estacionarias son particularmente f??ciles de calcular, ya que el componente transversal del campo el??ctrico y la componente normal del campo magn??tico debe desaparecer en la superficie de un conductor. Suponiendo que las placas paralelas se encuentran en el plano xy, las ondas estacionarias son

$\ Psi_n (x, y, z, t) = e ^ {- i \ omega_nt} e ^ {+ ik_xx ik_yy} \ sin \ left (k_n z \ right)$

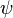donde $\ Psi$ representa el componente el??ctrica del campo electromagn??tico, y, por razones de brevedad, la la polarizaci??n y los componentes magn??ticos se ignoran aqu??. Aqu??, 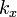$k_x$ y $k_y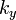$ son los vectores de onda en direcciones paralelas a las placas, y

$k_n = \ frac {n \ pi} {a}$

es el vector de onda perpendicular a las placas. Aqu??, n es un n??mero entero, como resultado de la exigencia de que ψ desaparecer en las placas de metal. La energ??a de esta onda es

$\ Omega_n = c \ sqrt {{k_x} ^ 2 + {k_y} ^ 2 + \ frac {n ^ 2 \ pi ^ 2} {a ^ 2}}$

donde c es la velocidad de la luz . La energ??a del vac??o es entonces la suma sobre todos los posibles modos de excitaci??n

$\ Langle E \ rangle = \ frac {\ hbar} {2} \ cdot 2 \ int \ frac {dk_x dk_y} {(2 \ pi) ^ 2} \ sum_ {n = 1} ^ \ infty A \ omega_n$

donde A es el ??rea de las placas de metal, y un factor de 2 se introduce para los dos posibles polarizaciones de la ola. Esta expresi??n es claramente infinita, y proceder con el c??lculo, es conveniente introducir una regulador (discutido en mayor detalle m??s adelante). El regulador servir?? para hacer la expresi??n finita, y en el fin, ??ste ser?? eliminado. La versi??n de la energ??a zeta-regulada por unidad de superficie de la placa es

$\ Frac {\ langle E (s) \ rangle} {A} = \ hbar \ int \ frac {dk_x dk_y} {(2 \ pi) ^ 2} \ sum_ {n = 1} ^ \ infty \ omega_n \ vert \ omega_n \ vert ^ {- s}$

Al final, el l??mite 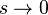$s \ a 0$ se que deban tomarse. Aqu?? s es un n??mero complejo , que no debe confundirse con la forma discutido previamente. Esta integral / suma es finita para s verdadero y m??s grande que 3. La suma tiene un polo en s = 3, pero puede ser anal??ticamente seguido s = 0, donde la expresi??n es finita. La expansi??n de este, se tiene

$\ Frac {\ langle E (s) \ rangle} {A} = \ frac {\ hbar c ^ {1-s}} {4 \ pi ^ 2} \ sum_n \ int_0 ^ \ infty 2 \ pi QDQ \ dej?? \ vert q ^ 2 + \ frac {\ pi ^ 2 n ^ 2} {a ^ 2} \ right \ vert ^ {(1-s) / 2}$

donde coordenadas polares 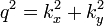$q ^ 2 = k_x ^ 2 + k_y ^ 2$ se introdujeron para encender la integral doble en un solo integrante. La 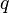$q$ en frente es el jacobiano, y la 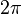$2 \ pi$ proviene de la integraci??n angular. La integral se realiza f??cilmente, resultando en

$\ Frac {\ langle E (s) \ rangle} {A} = - \ frac {\ hbar c ^ {1-s} \ pi ^ {2-s}} {2a ^ {3-s}} \ frac { 1} {3-s} \ sum_n \ vert n \ vert ^ {3} s$

La suma puede ser entendida como la Funci??n zeta de Riemann, y por lo que uno tiene

$\ Frac {\ langle E \ rangle} {A} = \ lim_ {s \ a 0} \ frac {\ langle E (s) \ rangle} {A} = - \ frac {\ hbar c \ pi ^ {2} } {6a ^ {3}} \ zeta (-3)$

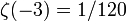Pero $\ Zeta (-3) = 1/120$ y por lo que se obtiene

$\ Frac {\ langle E \ rangle} {A} = \ frac {- \ hbar c \ pi ^ {2}} {3 \ cdot 240 a ^ {3}}$

La fuerza de Casimir por unidad de ??rea 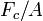$F_C / A$ para idealizada, la realizaci??n de placas perfectamente con vac??o entre ellos es

${F_C \ over A} = - \ frac {d} {da} \ frac {\ langle E \ rangle} {A} = - \ frac {\ hbar c \ pi ^ 2} {240 a ^ 4}$

donde

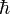$\ Hbar$ (Hbar, ℏ) es el constante reducida de Planck,

$c$ es la velocidad de la luz ,

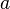$un$ es la distancia entre las dos placas.

La fuerza es negativa, indicando que la fuerza es atractiva: moviendo las dos placas m??s juntos, la energ??a se reduce. La presencia de 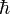$\ Hbar$ muestra que la fuerza por unidad de ??rea Casimir 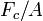$F_C / A$ es muy peque??o, y que, adem??s, la fuerza es inherentemente de origen de la mec??nica cu??ntica.

La teor??a m??s reciente

Un an??lisis muy completo del efecto Casimir en las distancias cortas se basa en un an??lisis detallado de la fuerza de van der Waals por Lifshitz. Usando este enfoque, las complicaciones de las superficies de delimitaci??n, tales como las modificaciones a la fuerza de Casimir debido a la conductividad finita se pueden calcular num??ricamente utilizando las funciones diel??ctricas complejos tabulados de los materiales de delimitaci??n. Adem??s de estos factores, las complicaciones surgen debido a la rugosidad superficial de la frontera y a la geometr??a efectos tales como el grado de paralelismo de las placas de delimitaci??n.

Para l??mites de las grandes separaciones, efectos de retardo dan lugar a una interacci??n de largo alcance. Para el caso de dos placas paralelas compuestas de metales ideales en vac??o, los resultados se reducen a Casimiro.

Medici??n

Una de las primeras pruebas experimentales se llev?? a cabo por Marcus Sparnaay en Philips en Eindhoven, en 1958, en un experimento delicado y dif??cil con placas paralelas, la obtenci??n de resultados no est?? en contradicci??n con la teor??a de Casimir, pero con grandes errores experimentales.

El efecto Casimir se midi?? con mayor precisi??n en 1997 por Steve K. Lamoreaux de Laboratorio Nacional de Los Alamos y por Umar Mohideen y Anushree Roy de la Universidad de California en Riverside. En la pr??ctica, en lugar de utilizar dos placas paralelas, lo que requerir??a la alineaci??n extraordinariamente precisa para asegurar que eran paralelo, los experimentos utilizan una placa que es plana y otra placa que es una parte de una esfera con un gran RADIUS. En 2001, un grupo en el Universidad de Padua finalmente tuvo ??xito en la medici??n de la fuerza de Casimir entre placas paralelas utilizando microresonators.

Regularizaci??n

Con el fin de ser capaz de realizar c??lculos en el caso general, es conveniente introducir una regulador en las sumas. Este es un dispositivo artificial, utilizado para hacer las sumas finita de modo que pueden ser manipulados m??s f??cilmente, seguido por la toma de un l??mite a fin de eliminar el regulador.

La n??cleo del calor o exponencialmente suma regulada es

$\ Langle E (t) \ rangle = \ frac {1} {2} \ sum_n \ hbar | \ omega_n | \ exp (-t | \ omega_n |)$

donde el l??mite 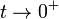$t \ a ^ 0 +$ se toma en el final. La divergencia de la suma se manifiesta t??picamente como

$\ Langle E (t) \ rangle = \ frac {C} {t ^ 3} + \ textrm {finito} \,$

para cavidades tridimensionales. La parte de la suma infinita se asocia con la constante C a granel que no depende de la forma de la cavidad. La parte interesante de la suma es la parte finita, que es la forma dependiente. La Regulador de Gauss

$\ Langle E (t) \ rangle = \ frac {1} {2} \ sum_n \ hbar | \ omega_n | \ exp (-t ^ 2 | \ omega_n | ^ 2)$

es m??s adecuado para los c??lculos num??ricos debido a sus propiedades de convergencia superiores, pero es m??s dif??cil de usar en los c??lculos te??ricos. Otros adecuadamente suaves, reguladores, se pueden usar tambi??n. La regulador de la funci??n zeta

$\ Langle E (s) \ rangle = \ frac {1} {2} \ sum_n \ hbar | \ omega_n | | \ omega_n | ^ {- s}$

es completamente inadecuado para los c??lculos num??ricos, pero es bastante ??til en los c??lculos te??ricos. En particular, las divergencias se muestran como polos en el plano complejo s , con la divergencia mayor en s = 4. Esta suma puede ser anal??ticamente continuado m??s all?? de este poste, para obtener una parte finita en s = 0.

No todas las configuraciones de cavidad conduce necesariamente a una parte finita (la falta de un polo en s = 0) o partes infinitas-forma independiente. En este caso, se debe entender que la f??sica adicional tiene que ser tomada en cuenta. En particular, en frecuencias extremadamente grandes (por encima de la plasma de frecuencia), los metales se vuelven transparentes a los fotones (como rayos X) y diel??ctricos muestran un corte de frecuencia dependiente tambi??n. Esta dependencia de la frecuencia act??a como un regulador natural. Hay una variedad de efectos a granel en f??sica del estado s??lido, matem??ticamente muy similar al efecto Casimir, donde el frecuencia de corte entra en juego expl??cito de mantener expresiones finito. (Estos se discuten en mayor detalle en Landau y Lifshitz, "Teor??a de los medios de comunicaci??n continuo").

Generalidades

El efecto Casimir tambi??n se puede calcular utilizando los mecanismos matem??ticos de integrales funcionales de la teor??a cu??ntica de campos, aunque estos c??lculos son considerablemente m??s abstracta, y por lo tanto dif??cil de comprender. Adem??s, pueden llevarse a cabo s??lo para el m??s simple de geometr??as. Sin embargo, el formalismo de la teor??a cu??ntica de campos deja claro que las sumas de valor esperado de vac??o son en cierto sentido sumatorias sobre el llamado " part??culas virtuales ".

M??s interesante es el entendimiento de que las sumas sobre las energ??as de ondas estacionarias deben entenderse formalmente como sumas sobre los valores propios de una Hamiltoniano. Esto permite que los efectos at??micos y moleculares, tales como la fuerza de van der Waals , debe entenderse como una variaci??n sobre el tema del efecto Casimir. De este modo se tiene en cuenta el hamiltoniano de un sistema como una funci??n de la disposici??n de objetos, tales como ??tomos, en espacio de configuraci??n. El cambio en la energ??a del punto cero como una funci??n de los cambios de la configuraci??n puede ser entendida para dar lugar a fuerzas que act??an entre los objetos.

En el modelo de bolsa quiral de la nucleon, la energ??a Casimir desempe??a un papel importante en la que muestra la masa del nucle??n es independiente del radio bolsa. Adem??s, el asimetr??a espectral se interpreta como un valor distinto de cero expectativa de vac??o de la n??mero de bariones, la cancelaci??n de la topol??gica n??mero de vueltas de la campo pion que rodea el nucle??n.

Efecto Casimir y agujeros de gusano

Se requiere materia ex??tica con densidad de energ??a negativa para estabilizar una agujero de gusano. Morris, Thorne y Yurtsever se??alaron que la mec??nica cu??ntica del efecto Casimir se pueden utilizar para producir una regi??n localmente masa-negativo de espacio-tiempo, y sugirieron que el efecto negativo podr??a ser utilizado para estabilizar un agujero de gusano para permitir viajar m??s r??pido que la luz. Esto se us?? en la novela Velocidad de la deformaci??n por Travis S. Taylor.

Analog??as

Un an??lisis similar se puede utilizar para explicar la radiaci??n Hawking que causa el lento " evaporaci??n "de los agujeros negros (aunque esto generalmente se visualiza como el escape de una part??cula a partir de una Part??culas virtuales par antipart??cula, la otra part??cula de haber sido capturada por el agujero negro).

Inversi??n

Mediante el uso de una perfecta lente (uno con la capacidad de enfocar una imagen con resoluci??n sin restricci??n por la longitud de onda de la luz) con un negativo ??ndice de refracci??n, el efecto puede invertirse, provocando peque??os objetos a ser repelidos m??s que atra??dos. Sin embargo, debido a la escala a la que se aplica el efecto, sus aplicaciones son m??s probable que se encuentre en nanotecnolog??a. Seg??n el profesor Ulf Leonhardt y el Dr. Thomas Philbin, de la Escuela de F??sica y Astronom??a de la Universidad, es te??ricamente posible hacer levitar objetos tan grandes como los seres humanos, pero los cient??ficos est??n muy lejos de desarrollar la tecnolog??a para tales haza??as.

Aplicaciones

Se ha sugerido que las fuerzas de Casimir tienen aplicaci??n en la nanotecnolog??a, en particular los sistemas de micro y nanoelectromec??nicos basados en la tecnolog??a de circuito integrado de silicio, y los llamados osciladores de Casimir.

Tecnolog??a

The Economist, 24 al 30 mayo 2008, destac?? aplicaciones pr??cticas del Efecto Casimir. Casimir "fricci??n est??tica", que es el foco de este art??culo afectar?? a los dise??os de los chips de computadora m??s peque??os. Adem??s, Casimir "repulsi??n", que se produce cuando un l??quido entre las placas promueve una fuerza de repulsi??n electromagn??tica que puede ser ??til en nanomec??nica.

Filosof??a

Debido a que el efecto Casimir basa en el hecho de que algo aparece com??nmente en la existencia de la vac??o, el efecto Casimir es utilizado por algunos como un argumento a favor de un origen puramente natural del universo.

Cultura popular

En relaci??n con la ciencia ficci??n, aunque la naturaleza del efecto no se ha revelado a??n, durante un v??deo de orientaci??n de la serie de TV Perdido, un Iniciativa Dharma m??dico (Dr. Edgar Halliwax) afirma que la isla exhibe un "efecto Casimir." Esto puede explicar por qu?? la Isla exhibe cualidades temporales extra??os como el tiempo de desplazamiento desde el resto del mundo. En el episodio final de su cuarta temporada, el efecto fue elaborado por la menci??n de una "bolsa de materia ex??tica cargada negativamente" y una aparente aparici??n de viaje en el tiempo.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Casimir_effect&oldid=226623963 "