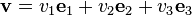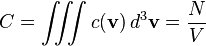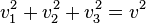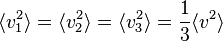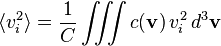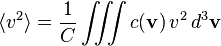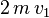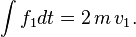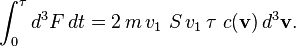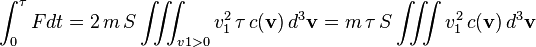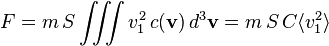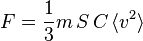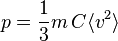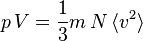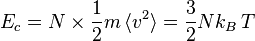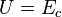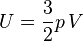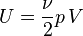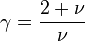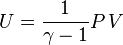Théorie cinétique des gaz
La théorie cinétique des gaz a pour objet d'expliquer le comportement macroscopique d'un gaz à partir des caractéristiques des mouvements des particules qui le composent. Elle permet notamment de donner une interprétation microscopique aux notions de :
- température : c'est une mesure de l'agitation des particules, plus précisément de leur énergie cinétique ;
- pression : la pression exercée par un gaz sur une paroi résulte des chocs des particules sur cette dernière. Elle est liée à leur quantité de mouvement
La théorie cinétique des gaz a été développée à partir du XVIIIe siècle. Elle est fondée sur les idées de Daniel Bernoulli, John James Waterston, K.A. Krönig et Rudolf Clausius. James Clerk Maxwell et Ludwig Boltzmann ont formalisé son expression mathématique[1]. Les succès de la théorique cinétique des gaz ont constitué un argument fondamental à l'appui de la théorie atomique de la matière.
Selon les hypothèses retenues, la théorie peut être plus ou moins complexe et rendre compte de plusieurs phénomènes :
- dans sa version la plus simple, on ignore les interactions entre les molécules, ainsi que leur taille. Elle permet de retrouver la loi des gaz parfaits ;
- en prenant en compte les effets de taille des molécules, on peut décrire les collisions entre les molécules, ce qui donne accès aux propriétés de transport (viscosité, diffusion de la matière, effusion, conductibilité thermique) ;
- en introduisant de plus des interactions entre particules, Johannes Diderik van der Waals a proposé en 1873 une équation qui porte son nom et permet de décrire également la transition liquide-gaz (ébullition, évaporation, condensation). Elle a servi de guide à ceux qui, dans la seconde moitié du XIXe siècle, cherchaient à liquéfier tous les gaz, jusqu'à l'hélium, liquéfié en 1908 à Leyde.
Description

Un gaz est un ensemble d'atomes ou de molécules subissant un certain nombre d’interactions : notamment les chocs entre particules et avec la paroi du récipient qui les contient ; des interactions de nature électromagnétique (comme les forces de van der Waals) ; une agitation aléatoire de nature quantique[2] ; les molécules poly-atomiques sont l'objet de mouvements d'agitation interne qui intervient dans la capacité thermique des corps[3].
Dans le cadre de la théorie cinétique, on fait les approximations suivantes :
- le volume des molécules est négligeable
- seuls les chocs ont une influence, les autres interactions sont négligeables.
La trajectoire des molécules peut se modéliser avec le mouvement brownien.
- Approche intuitive du mouvement des molécules
Supposons que dans un récipient, toutes les molécules ont la même vitesse et la même direction. Ce système est instable parce que la moindre modification de trajectoire d'une seule molécule provoquera le heurt sur une autre molécule qui déviera et heurtera encore une autre avec un effet en chaîne qui établira le chaos donc le mouvement brownien.
- Dans la suite,
- P, désigne la pression du gaz,
- V, son volume,
- T, sa température thermodynamique, et
- N, le nombre de molécules.
Vitesse et pression
Statistiques sur les vitesses
Considérons une molécule ayant une vitesse de norme[4] v et frappant une surface. Elle subit un choc élastique, c'est-à-dire qu'elle repart en faisant un même angle avec la surface, avec une vitesse de même norme v[5]. Si l'on choisit un repère orthonormé[6] e1, e2, e3, avec e1 perpendiculaire à la surface, alors cette vitesse se décompose selon les trois axes
On appelle c(v) d3v le nombre de molécules par unité de volume (la concentration) dont la vitesse est comprise dans un volume infinitésimal d3v autour de la valeur v. La concentration globale est donc :
La répartition statistique des vitesses étant isotrope, la moyenne des composantes de la vitesse est évidemment nulle :
-
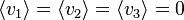 [7]
[7]
Les moyennes quadratiques ne sont par contre pas nulles[8], et elles sont égales entre elles par symétrie de rotation. Comme on a toujours
(théorème de Pythagore), on a en moyenne
avec
et
On appelle u la vitesse quadratique moyenne, telle que :
-
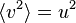 .
.
La loi de distribution des vitesses de Maxwell indique que plus le gaz a une température élevée , plus u est grande : 1/2 m u² = 3/2 kT , k étant la constante de Boltzmann
Impact d'une molécule
Lorsqu'une molécule de masse m rebondit de manière élastique sur la surface, la composante 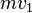 perpendiculaire à la surface de sa quantité de mouvement varie de[9] :
perpendiculaire à la surface de sa quantité de mouvement varie de[9] :
D'après les lois de Newton (principe fondamental de la dynamique et théorème des actions réciproques), l'intégrale en temps de la force qu'elle imprime sur la surface est donc :
Impact de toutes les molécules
On cherche maintenant, v étant fixé à d3v près, à savoir combien de molécules frappent une petite surface d'aire S durant une durée τ.
Les molécules frappant la surface entre l'instant 0 et l'instant τ sont nécessairement dans un cylindre de base S et de hauteur v1τ — les autres molécules sont trop loin ou frappent à côté. Ce cylindre d'axe v a un volume de S v1 τ. La force d3F créée par toutes les molécules considérées est donc :
La force F créée par toutes les molécules s'obtient en intégrant sur v1 > 0 si l'on oriente e1 du gaz vers l'extérieur (on ne considère que les molécules allant vers la surface, pas celles s'en éloignant). Ceci revient à diviser par deux, en raison de la symétrie de la distribution c(v) :
En négligeant les fluctuations dans le temps de F, on peut intégrer sur t et simplifier par τ :
ou
La pression étant la force divisée par la surface, on obtient
ou encore, par définition de C = N / V :
Pression et énergie cinétique
Si une molécule de masse m se déplace à une vitesse v, son énergie cinétique vaut 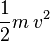 et l'énergie cinétique totale des molécules du gaz vaut, par définition de la température absolue :
et l'énergie cinétique totale des molécules du gaz vaut, par définition de la température absolue :
Où kB est la constante de Boltzmann, N le nombre de particules et T la température (en kelvins).
Il reste à démontrer que cette quantité se comporte bien comme une température ; c'est un point délicat, comme Feynman le déclare ( in Lectures on Physics ).
Gaz parfait monoatomique
Dans le cas d'un gaz parfait monoatomique, on suppose que la totalité de l'énergie est sous forme d'énergie cinétique des molécules (énergie thermique), donc l'énergie interne U du système vaut :
On a donc
Gaz parfait de Laplace
Dans le cas plus général du gaz parfait de Laplace, on suppose que les molécules ont une énergie interne de rotation ou d'oscillation, proportionnelle à 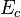 .
Le nombre de degrés de liberté passe de 3 à
.
Le nombre de degrés de liberté passe de 3 à 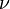 et dans l'hypothèse d'équipartition, on a
et dans l'hypothèse d'équipartition, on a 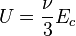 ,
et donc
,
et donc
En modifiant adiabatiquement le volume du gaz, on fournit un travail 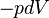 égal à la variation d'énergie interne
égal à la variation d'énergie interne 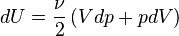 .
Donc on a
.
Donc on a 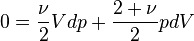 ou
ou
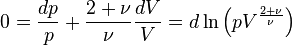 .
Traditionnellement, pour retrouver la loi de Laplace du gaz parfait en régime adiabatique
.
Traditionnellement, pour retrouver la loi de Laplace du gaz parfait en régime adiabatique 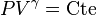 , on introduit
, on introduit
Pour le gaz parfait de Laplace, on a donc
- Pour un gaz réel monoatomique, ou même l'hydrogène à très basse température
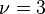 et
et 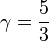
- Pour un gaz réel diatomique à température intermédiaire (azote, hydrogène, oxygène autour de 300 K), on a deux degrés de rotation possible
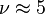 et
et 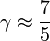
- Pour un gaz réel diatomique à très haute température, l'oscillation longitudinale devient possible, et
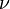 tend vers 7 et
tend vers 7 et 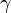 tend vers
tend vers 
Notes et références
- ↑ Samuel Glasstone, Textbook of Physical Chemistry - second edition p.248
- ↑ Voir Énergie du point zéro.
- ↑ Voir : Température thermodynamique.
- ↑ Dans notre cas une vitesse de grandeur et de direction définie
- ↑ C’est-à-dire avec la même vitesse numérique
- ↑ C’est-à-dire, dans notre cas, un trièdre rectangle
- ↑ La vitesse isotrope prend la même valeur dans toutes les directions et toutes les directions sont également probables
- ↑ Une vitesse dans une direction et la même dans la direction opposée ont le même carré
- ↑ À l'arrivée, elle a une quantité de mouvement de mv1 au retour sa quantité de mouvement est -mv1. Les composantes parallèles à la paroi sont supposées ne pas varier. La différence est donc 2mv1.
Voir aussi
Articles connexes
- Équation de Boltzmann
- Loi de distribution des vitesses de Maxwell
- Physique statistique
- Pression cinétique
Bibliographie
- Ludwig Boltzmann, Leçons sur la théorie des gaz, Gauthier-Villars, 1902-1905 (ISBN 2-87647-004-7)Réédition Jacques Gabay (1987)
- Carlo Cercignani, Ludwig Boltzmann - The man who Trusted Atoms, Oxford University Press, , 330 p. (ISBN 0-19-850154-4)Biographie scientifique du grand professeur Boltzmann, qui a porté la théorie cinétique des gaz à son acmée. Par un professeur de Physique Mathématique de l'Université de Milan (Italie), spécialiste de l'équation de Boltzmann. Niveau plutôt second cycle universitaire
- Yves Rocard, L'Hydrodynamique et la théorie cinétique des gaz (thèse), Masson et Cie, , 128 p. [(fr) lire en ligne]
Lien externe
- Simulation d'un gaz à deux dimensions de 2000 molécules circulaires maximum. Université Paris XI
- Portail de la chimie
- Portail de la physique