Percolation
La percolation (du latin percolare, « filtrer », « passer au travers ») désigne communement le passage d'un fluide à travers un milieu plus ou moins perméable, par exemple dans la préparation du café.
Ce terme a aussi un sens plus précis en physique et en mathématiques : c'est un processus physique critique qui décrit, pour un système, une transition d’un état vers un autre. C'est un phénomène de seuil associé à la transmission d'une « information » par le biais d'un réseau de sites et de liens qui peuvent, selon leur état, relayer ou non l'information aux sites voisins.
Histoire
Vers 1800, le Français Jean Baptiste de Belloy, archevêque de Paris, invente le système de la percolation du café, auparavant infusé, ainsi son dubelloire ou sa débelloire devient la première cafetière.
En 1856, Henry Darcy formule « la loi de Darcy » dans l'appendice D de son ouvrage Les fontaines publiques de la ville de Dijon[1], ou il traite de la perméabilité d'un sol en fonction de la hauteur d'eau. Son étude ne concerne cependant que des milieux perméables, et aucun effet de seuil n'est mis en évidence.
Le phénomène de seuil est étudié pour la première fois en 1957 par John Hammersley (en) qui cherche à comprendre comment les masques à gaz des soldats deviennent inefficaces[2]. Le terme de « percolation » vient du phénomène analogue qu'est le passage non plus d'un gaz, mais de l'eau à travers le percolateur de la machine à café qui est un filtre au même titre que le masque à gaz[3].
Hammersley en généralise le sens à la transmission, ou non, d'une « information » par un réseau de sites et de liens. Dans le cas particulier de la physique des fluides, l'information est le fluide (eau ou gaz), et les sites sont les pores du filtre qui relayent l'information s'ils ne sont pas bouchés.
Percolation quantifiant la perméabilité
Géologie

La percolation de l'eau à travers les sols est étudiée dans le cadre de l'écologie urbaine. Il s'agit de limiter les inondations, et subséquemment les sécheresses.
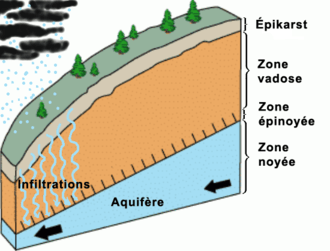
En pédologie, la percolation est un écoulement d'eau dans la couverture pédologique perméable, sous l'effet de la gravité. La loi de Darcy décrit le lien entre hauteur d'eau et vitesse de percolation, par exemple dans le cas d'une eau de surface qui alimente une nappe phréatique. Mais cette loi décrit la perméabilité du milieu en fonction de la quantité d'eau, sans prendre en compte un effet de seuil.
Préparation de boissons

Le café peut être obtenu par percolation, en utilisant un percolateur (en). C'est la méthode utilisé dans la préparation de l'expresso[4].
Dans l'hôtellerie, le thé infusé est obtenu par percolation sous haute pression.
Approches théoriques de la percolation
Théorie de la percolation de Hammersley
Cette théorie développée par Hammersley définit une probabilité critique pc, et les régimes associés (sous-critiques, critiques et sur-critiques), de connecter des points en un amas de taille infinie. Une des applications de la théorie de la percolation est l'étude des feux de forêts (et de façon proche la propagation des épidémies[2]).
Théorie des systèmes dynamiques
La théorie des systèmes dynamiques et celle de la percolation convergent sur la notion de « fragilité » : plus un système est fragile (c'est-à-dire qu'il peut subir des changements brusques d'un état à un autre), plus il peut être assimilé à une structure poreuse, perméable et manquant de rigidité. La percolation permet alors de juger du seuil critique de transformation de ce système.
En théorie des systèmes dynamiques, la percolation est donc le passage d'un système d'un état (ou une phase) vers un état inférieur et moins performant (entropie) ou supérieur et plus performant (auto-organisation, néguentropie). Cette mutation se produit soit de façon soudaine et abrupte, soit en passant par une « phase de transition » plus ou moins indécise et plus ou moins chaotique ou au contraire peu active (stase).
La théorie de la percolation peut aussi être utilisé en économie, en écologie (pour étudier des migrations), en sociologie etc.[5]
Voir aussi
- Osmose
- Effet de seuil
- Algorithme de Hoshen-Kopelman
Liens externes
- La percolation sur le site OpenClassrooms
- Article La percolation, un jeu de pavages aléatoires de Hugo Duminil-Copin pour Images des Maths et Pour la science.
- Exemples de percolation dans la thèse de Stephane Pajot
- Percolation et économie : Modèles de percolation et apports de la percolation à la théorie économique
- Propriétés remarquables de pions sur un hexiquier par Edouard Rodrigues: Il existe non pas toujours une seule chaîne traversant un pavage hexagonal mais il existe toujours 2 chaines traversant un pavage hexagonal quelconque.
Notes et références
- ↑ Henry Darcy, Les fontaines publiques de la ville de Dijon : exposition et application des principes à suivre et des formules à employer dans les questions de distribution d'eau, Paris, Victor Dalmont, (lire en ligne)
- 1 2 Article La percolation, un jeu de pavages aléatoires de Hugo Duminil-Copin pour Images des Maths et Pour la science.
- ↑ L'origine étymologique est reprise dans la thèse "Percolation et économie" de Stéphane Pajot, 2001 (lien pérenne : http://www.theses.fr/2001NANT4007).
- ↑ Voir M. Petracco, « Percolation », dans Espresso coffee: the science of quality, Academic Press,
- ↑ Voir l'article Théorie de la percolation pour plus de détails.
- Portail des sciences