Notae priores

Les Notae priores ou Ad Logiticem speciosam Nota priores est le nom du premier livre d'algèbre prévu par François Viète pour succéder à son Isagoge. Dans ce livre, Viète donne les éléments préparatoires à la résolution des équations du troisième degré sans utiliser les complexes. Elles sont suivies dans l'ordre chronologique de ses publications par les Zeteticorum libri quinque.

Origines

Les algébristes italiens du XVIe siècle sont parvenus à résoudre les équations du troisième degré en formant les premiers des solutions imaginaires. Pour autant, ils ne donnent de formules que dans des cas particuliers, en utilisant une symbolique difficile à légitimer aux yeux des mathématiciens de l'époque, pour qui la seule axiomatique admissible est celle d'Euclide, en géométrie.

Viète accomplit le même travail que les algébristes italiens, mais en usant de calculs géométriques, dans les triangles rectangles. Il développe à cet effet une théorie des puissances d'un triangle, et des produits de deux triangles, tout à fait comparable aux calculs des italiens dans les complexes. Mais, accomplissant ce travail dans son propre langage symbolique, il atteint par ce biais une résolution générale de ces équations.

Contenu

Généralités

Le traité se décompose en deux parties, l'une algébrique, l'autre géométrique. Les premières propositions préparent le travail ultérieur :

Proposition I : Trois grandeurs étant données trouver une quatrième proportionnelle.

Proposition II : Deux grandeurs étant données, trouver une troisième proportionnelle, une quatrième, une cinquième, et d'autres grandeurs continuellement proportionnelles d'ordre ultérieur, jusqu'à l'infini.

Proposition III : Trouver une moyenne proportionnelle entre deux carrés donnés.

Proposition IV : Trouver deux moyennes continuellement proportionnelles entre deux cubes donnés

Proposition V : Entre deux côtés donnés, trouver un nombre quelconque de moyennes continuellement proportionnelles. À quoi Viète donne comme solution : A carré-cube, A carré-carré par B, A cube par B carré, A carré par B cube,A par B carré-carré et B carré cube.

Proposition VI : À la somme de deux grandeurs ajouter leur différence. À quoi répond le théorème : La somme de deux grandeurs ajoutée à leur différence est égale au double de la plus grande.

(la différence étant prise en valeur absolue)

Proposition VII : De la somme de deux grandeurs retrancher leur différence. À quoi répond le théorème : La somme de deux grandeurs diminuée de leur différence, est égale au double de la plus petite.

Proposition VIII : Lorsqu'une même grandeur est diminuée de quantités inégales, retrancher l'une des différences de l'autre. À quoi répond le théorème : Si une grandeur est diminuée de quantités inégales, la différence de restes est la même que la différence des quantités soustraites.

La démarche est identique pour les propositions qui suivent :

Proposition IX : Lorsqu'une même grandeur est augmentée de quantités inégales, retrancher l'une des sommes de l'autre.

Proposition X : Lorsqu'une même grandeur est augmentée et diminuée de quantités inégales, retrancher l'une de l'autre.

Le binôme de Newton

Viennent alors des propositions relevant du développement du binôme.

Proposition XI : Former une puissance pure d'une racine binôme. Viète donne ici les développements du carré de A+B, de son cube, du carré-carré, et ainsi de suite jusqu'au cubo-cube, reconnaissant une règle de formation des monômes et l'identité de lecture gauche droite du développement du binôme.

Proposition XII : Au carré de la somme des côtes, ajouter le carré de leur différence. À quoi répond le théorème : Le carré de la somme des côtés plus le carré de leur différence est égal à deux fois la somme des carrés.

Proposition XIII : Du carré de la somme des deux côtes retrancher le carré de leur différence. À quoi répond le théorème : Le carré de la somme de deux côtés moins le carré de leur différence est égale à quatre fois le produit plan de ces côtés. Puis une remarque importante, notée dans un langage contemporain

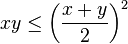
xy\leq\left({x+y\over 2}\right)^2

Les identités remarquables

Viennent quelques identités remarquables :

Proposition XIV : Multiplier la différence de deux côtés par leur somme.

Proposition XV : Au cube de la somme de deux côtés ajouter le cube de leur différence.

Proposition XVI :Du cube de la somme de deux côtes retrancher le cube de leur différence.

Proposition XVII : Multiplier la différence de deux côtés par les trois plans partiels, qui composent le carré de la somme des mêmes côtés, ces plans étant pris une fois seulement. Ce qui traduit en théorème donne

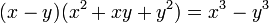
(x-y)(x^2+xy+y^2)=x^3-y^3

Proposition XVIII : Multiplier la somme de deux côtés par les trois plans partiels, qui composent le carré de la différence des mêmes côtés, ces plans étant pris une fois seulement. Ce qui traduit en théorème donne

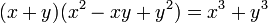
(x+y)(x^2-xy+y^2)=x^3+y^3

Proposition XIX : Multiplier la différence de deux côtés par les quatre solides partiels, qui composent le cube de la somme des mêmes côtés, ces solides étant pris une fois seulement. Ce qui traduit en théorème donne

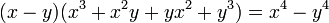
(x-y)(x^3+x^2y+yx^2+y^3)=x^4-y^4

Proposition XX : Multiplier la somme de deux côtes par les quatre solides partiels, qui composent le cube de la différence des mêmes côtés, ces solides étant pris une fois seulement. Ce qui traduit en théorème donne

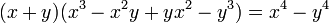
(x+y)(x^3-x^2y+yx^2-y^3)=x^4-y^4

Les propositions qui suivent,

Proposition XXI donnant

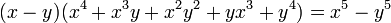(x-y)(x^4+x^3y+x^2 y^2 +yx^3+y^4)=x^5-y^5

et l'analogue Proposition XXII ainsi que les deux suivantes, du degré 6 terminent cette première collection de formules de base. Viète les généralise sous forme de deux théorèmes. On donne le second :

« Le produit de la somme de deux côtés par les termes homogènes, qui composent la puissance de la différence des mêmes côtés, ces termes étant pris une fois seulement, est égal à la somme où à la différence des puissances de l'ordre immédiatement supérieur, c'est-à-dire à la somme, si le nombre des termes homogènes est impair, et à la différence, si le nombre des termes homogènes est pair. »

Baldassare Boncompagni

Préparations à la résolution d'équations

Les propositions d'après sont à la base de la résolution des équations exposée par Viète dans le Numerosa Potestate. Elles sont extrêmement répétitives, vu l'impossibilité pour Viète de donner un sens à une longueur orienté (ce travail ne sera accompli qu'au XIX^e siècle par Hermann Grassmann avec la création de l'algèbre extérieure). Les propositions XXV à XXXIII apprennent à former par exemple le carré affecté par l'addition du plan sous le côté, produit par un coefficient sous latéral de longueur convenablement choisi c'est-à-dire, selon l'écriture moderne à constater que

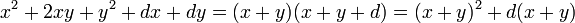x^2+2xy+y^2+dx+dy=(x+y)(x+y+d)=(x+y)^2+d(x+y)

et ainsi de suite jusqu'au développement de

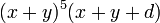(x+y)^5(x+y+d)

. Les propositions XXXIV à XXXVI reprennent les précédentes avec une soustraction, Les propositions XXXVII à IXL mêlent soustraction et addition dans le même esprit. Les propositions XL à XLIV reprennent les mêmes développement pour

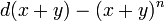d(x+y)-(x+y)^n

, pour n entre 2 et 6.

Complexes et triangles rectangles

Dans une dernière partie, Viète s'attaque à la représentation par des figures (des triangles) d'un certain nombre de problèmes classiques.

Proposition XLV : Avec deux racines données former un triangle rectangle. Cela revient à vérifier géométriquement que

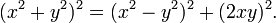
(x^2+y^2)^2=(x^2-y^2)^2+(2xy)^2.

Proposition XLVI: Avec deux triangles rectangles former un troisième triangle rectangle. Cela revient à montrer que pour

x,y,z,t

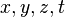, on a

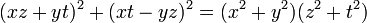(xz+yt)^2+(xt-yz)^2=(x^2+y^2)(z^2+t^2)

, identité qui prend tout son sens si on la lit comme le produit des carrés des modules de deux nombres complexes. On l'attribue généralement à Lagrange. Viète retrouve ainsi, géométriquement, les principes à la base du calcul des imaginaires, initiés 50 ans plus tôt par Scipione del Ferro. Mais le lien entre ces formules géométriques et leurs équivalents complexes ne sera véritablement établi qu'au XIX^e siècle, par Gauss.

Viète résout par la suite les problèmes suivants :

Proposition XLVII : Avec deux triangles rectangles semblables former un troisième triangle rectangle tel que le carré de l'hypoténuse du troisième soit égal a la somme des carrés de l'hypoténuse du premier et de l'hypoténuse du second.

Proposition XLVII : Avec deux triangles rectangles égaux et équiangles, former un troisième triangle rectangle.

Proposition XLVIII : Avec le triangle rectangle de l'angle simple, et le triangle rectangle de l'angle double former un triangle rectangle. Ce troisième triangle sera nommé « triangle de l'angle triple ».

Il joue par la suite (jusqu'à la Proposition LI) avec l'angle triple, l'angle quadruple, puis poursuit à l'ordre supérieur, et ainsi de suite à l'infini, découvrant géométriquement (et sans le dire explicitement puisque Viète ne reconnaît pas l'existence des imaginaires) que les parties réelles et imaginaires de

(x+Iy)^n

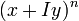s'obtiennent en fait en alternant les coefficients des binômes qu'il a développés dans les précédentes parties.

Suivent d'autres propositions, qui forment le sommet de cet art, qu'on peut interpréter en termes complexes, et dont la solution géométrique figureici :

Proposition LII : Composer un triangle rectangle avec la somme de deux racines et leur différence.

Proposition LIII : Avec la base d'un triangle rectangle donné et la somme de son hypoténuse et de sa perpendiculaire, former un triangle rectangle.

Proposition LIV : Déduire d'un triangle rectangle deux triangles rectangles de même hauteur, tels que le triangle de même hauteur formé par leur juxtaposition (dont les cathètes seront les hypoténuses de ces triangles, et dont la base sera la somme de leurs bases) aura l'angle au sommet droit.

Devenir

Les manuscrits de Viète entrent à sa mort en possession de Pierre puis de Jacques Aleaume. Les Notae priores ne font pas partie des manuscrits donnés à Alexander Anderson (mathématicien). Le texte, qui devait suivre l'Isagoge en 1591 et n'avait jamais été publié du vivant de Viète, est publié pour la première fois par Jean de Beaugrand en 1631, puis par Van Schooten en 1646 avec quelques commentaires de Jean de Beaugrand^[1]. Il a été traduit en français par Frédéric Ritter.

Ingénieur des ponts et chaussées en poste à Fontenay le Comte, Frédéric Ritter a publié sa traduction dans le bulletin du comte Baldassare Boncompagni^[2] en 1868.

Notes et références

↑ P. Radelet-de Grave, Liber amicorum Jean Dhombres, vol. 8 : Réminisciences, Centre de recherche en histoire des sciences,‎ 2008, 582 p. (ISBN 9782503528144), p. 19 et 61
↑ Da. B. Boncopagni Bullettino di bibliografia e di storia delle science matematicheVolume 1 Rome 1868

Portail des mathématiques
Portail de la France
Portail de la Renaissance
Portail algèbre nouvelle et François Viète

This article is issued from Wikipédia - version of the Sunday, May 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.