Moment cinétique (mécanique classique)

Pour les articles homonymes, voir Moment.

Moment cinétique

Description de cette image, également commentée ci-après

Un gyroscope tournant sur un clou.

Données clés
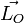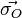Symbole usuel	$\vec{L_O}$ ou $\vec{\sigma_O}$
Unités SI	kg.m².s^-1
Dimension	M.L².T^-1
Grandeur extensive	oui
Grandeur conservative	oui
Nature	vecteur (mécanique classique), opérateur (mécanique quantique), tenseur (relativité restreinte)
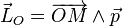Expressions	$\vec{L}_O = \overrightarrow{OM}\wedge\vec{p}$

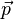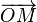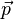En physique, le moment cinétique ou moment angulaire d'un point matériel M est le moment de la quantité de mouvement $\vec{p}$ par rapport à un point O, c'est-à-dire le produit vectoriel de $\overrightarrow{OM}$ et de $\vec{p}$ . C'est un champ équiprojectif, donc un torseur.

Cette grandeur physique joue dans le cas d'une rotation, un rôle analogue à celui de la quantité de mouvement pour une translation : si la conservation de la quantité de mouvement pour un système isolé est liée à l'invariance par translation dans l'espace (propriété d'homogénéité de l'espace), la conservation du moment cinétique est liée à l'isotropie de l'espace.

De façon plus générale, si pour un système quelconque (dans un référentiel galiléen), la variation temporelle de la quantité de mouvement (du centre d'inertie) est donnée par la somme des forces extérieures agissant sur le système d'après la relation fondamentale de la dynamique, la variation temporelle du moment cinétique est liée à la somme des moments des forces extérieures agissant sur ce même système. De même, dans le cas d'un solide l'énergie cinétique totale se décompose en l'énergie du centre d'inertie, proportionnelle au carré de la quantité de mouvement du centre d'inertie, et un terme faisant intervenir le moment cinétique propre du solide, lié à sa rotation propre.

Le lien entre moment angulaire et rotation est encore plus net en mécanique analytique et surtout en mécanique quantique (cf. moment cinétique en mécanique quantique) où ce concept est enrichi, avec l'apparition de moment cinétique sans équivalent classique (cf. notion de spin).

Le moment angulaire dépend non seulement du référentiel d'étude (R) mais aussi du choix de l'origine O, par suite, il n'est pas possible de combiner en général des moments angulaires ayant des origines différentes. Son unité est le kg.m².s^-1.

Cas d'un point matériel

La notion de "point matériel" (ou corps ponctuel) correspond à une idéalisation d'un système mécanique où les dimensions de celui-ci sont considérées comme petites devant les distances caractéristiques du mouvement étudié (distance parcourue, rayon d'une orbite…). Le système est alors modélisé par un simple point géométrique (noté M) auquel est associé sa masse m. Ce modèle du point matériel permet d'introduire simplement la notion de moment cinétique, qui peut être généralisée par additivité à un système quelconque, considéré comme un ensemble de points matériels.

Définition

Pour un point matériel en mouvement par rapport à un référentiel donné, 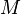$M$ de vecteur position 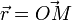$\vec{r}=\vec{OM}$ , le moment cinétique (ou angulaire) 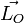$\vec{L_O}$ par rapport à un point O choisi pour origine est défini par^[1]:

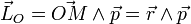\vec{L}_O=\vec{OM} \wedge \vec{p}=\vec{r}\wedge \vec{p}

où 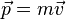$\vec{p}=m\vec{v}$ est la quantité de mouvement de la particule. Le moment cinétique est donc le moment de cette dernière par rapport à 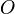$O$ . Il dépend bien sûr du point O ainsi que du référentiel d'étude.

De façon évidente si le mouvement du point matériel par rapport au référentiel considéré est rectiligne, et que le point O se trouve sur la trajectoire, les vecteurs position et quantité de mouvement seront colinéaires, et le moment cinétique sera nul. En revanche, pour un point O en dehors de la trajectoire, du point de vue duquel la direction de 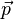$\vec{p}$ "tourne" par rapport à celle de 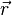$\vec{r}$ , cela ne sera plus vrai et le moment cinétique ne sera plus nul, ni constant d'ailleurs. Intuitivement, ceci permet de voir que 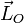$\vec{L}_O$ est lié d'une certaine manière à la "rotation" du point matériel M autour de l'origine O.

Il est possible de traduire cette vision intuitive de façon générale et quantitative en établissant la relation entre sa variation temporelle (dérivée) du moment cinétique et la somme des moments des forces extérieures appliquées au système: c'est le théorème du moment cinétique.

Théorème du moment cinétique pour un point matériel

La dérivation membre à membre de l'expression du moment angulaire, permet d'obtenir (O étant supposé fixe dans le référentiel d'étude (R)):

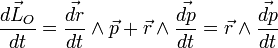\frac{\vec{dL_{O}}}{dt}=\frac{\vec{dr}}{dt}\wedge \vec{p}+\vec{r}\wedge \frac{\vec{dp}}{dt}=\vec{r}\wedge \frac{\vec{dp}}{dt}

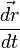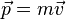puisque $\frac{\vec{dr}}{dt}$ et $\vec{p}=m\vec{v}$ sont colinéaires.

Pour un point matériel la relation fondamentale de la dynamique s'écrit:

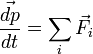\frac{\vec{dp}}{dt}=\sum_{i} \vec{F_{i}}

le terme de droite représentant la somme des forces 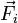$\vec{F_{i}}$ (réelles ou "d'inertie") exercées sur le corps.

En tenant compte de ceci dans l'expression de la dérivée du moment cinétique il vient l'équation suivante, dite théorème du moment cinétique:

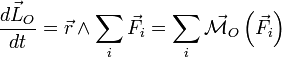\frac{\vec{dL_{O}}}{dt}=\vec{r}\wedge \sum_{i} \vec{F_{i}}=\sum_{i} \vec{\mathcal{M}_{O}}\left (\vec{F_{i}}\right)

^[2],

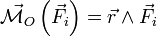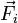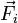où $\vec{\mathcal{M}_{O}}\left ( \vec{F_{i}}\right)= \vec{r}\wedge \vec{F_{i}}$ est le moment de la force $\vec{F_{i}}$ par rapport au point O. Cette grandeur (appelée en anglais torque) correspond donc à la variation du moment cinétique en O qu'engendre l'action de la force $\vec{F_{i}}$ .

Il est alors évident que si le moment résultant 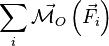$\sum_{i} \vec{\mathcal{M}_{O}}\left (\vec{F_{i}}\right)$ est nul le moment cinétique 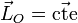$\vec{L}_O=\vec{\text{cte}}$ est une integrale première du mouvement.

Interprétation physique:' le théorème du moment cinétique est similaire dans sa forme à la relation fondamentale de la dynamique. Si cette dernière relie forces appliquées au point matériel et variation de sa quantité de mouvement, le théorème du moment cinétique relie la somme des moments de ces forces par rapport à un point donné et variation du moment cinétique par rapport à ce même point. Or le moment d'une force par rapport à un point traduit en quelque sorte la "propension" de cette force à faire "tourner" le système autour de ce point^[3]. Intuitivement, le théorème du moment cinétique est une sorte d'équivalent de la relation fondamentale de la dynamique pour ce qui est de la rotation du point M par rapport à O. Toutefois, c'est dans le formalisme de la mécanique analytique que la relation étroite entre moment cinétique et rotations spatiales devient nettement plus claire.

Exemples d'application

Un exemple simple est celui d'une particule décrivant un cercle de centre 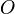$O$ et de rayon 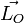$r$ : $\vec{L_{O}}$ est dirigé selon l'axe du disque et vaut 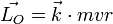$\vec{L_{O}} = \vec{k} \cdot mvr$ . Le sens 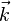$\vec{k}$ du vecteur moment cinétique ne recouvre pas une réalité physique mais est une convention ; c'est un vecteur axial.

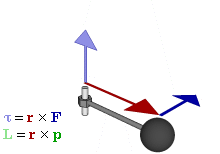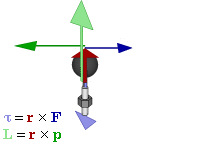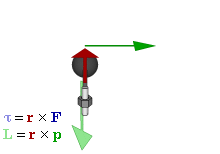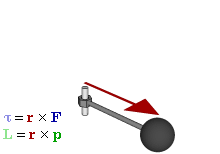
La figure ci-contre permet de préciser les relations entre les diverses grandeurs physiques.

Par analogie avec la quantité de mouvement, le moment cinétique permet de définir l'analogue de la masse : le moment d'inertie 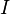$I$ . En effet

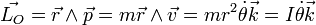\vec{L_{O}}=\vec{r}\wedge \vec{p}=m \vec{r}\wedge \vec{v}= mr^{2}\dot{\theta} \vec{k} = I \dot{\theta} \vec{k}

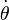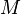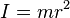$\dot{\theta}$ étant la vitesse angulaire du point $M$ ), et $I=mr^{2}$ . La notion de moment d'inertie est détaillée plus loin dans la partie consacrée à la définition du moment cinétique pour un système matériel.

En faisant correspondre à la vitesse angulaire 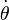$\dot{\theta}$ du point matériel le vecteur axial 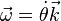$\vec{\omega}=\dot{\theta} \vec{k}$ , dit vecteur rotation, le moment cinétique s'écrit finalement dans ce cas:

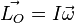\vec{L_{O}}= I \vec{\omega}

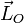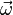Dans le cas d'un solide, le moment cinétique et le vecteur rotation instantanée ne sont pas en général colinéaire, la relation entre $\vec{L}_O$ et $\vec{\omega}$ fait alors intervenir un tenseur, dit d'inertie, généralisant la notion précédente.

Moment cinétique et isotropie

La notion d'isotropie de l'espace traduit l'équivalence de toutes les directions dans celui-ci: dire que l'espace est isotrope signifie donc aussi qu'il est invariant par toute rotation spatiale autour d'un point quelconque. Cette propriété est en particulier valable pour un système dit isolé, c'est-à-dire qui n'est soumis à aucune action extérieure.

Dans le formalisme hamiltonien^[4], cela implique que la fonction de Hamilton 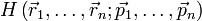$H\left(\vec{r}_1,\ldots,\vec{r}_n;\vec{p}_1,\ldots,\vec{p}_n\right)$ de tout système isolé de n points matériels soit invariante par toute rotation globale du système autour de l'origine O (arbitraire). 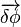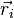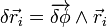En particulier, cela sera valable pour une rotation élémentaire arbitraire de vecteur $\overrightarrow{\delta\phi}$ , telle que la variation du vecteur position $\vec{r}_i$ soit donnée par $\delta\vec{r}_i=\overrightarrow{\delta\phi}\wedge\vec{r}_i$ .

En coordonnées cartésiennes les impulsions généralisées 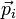$\vec{p}_i$ sont identiques aux quantités de mouvement des différents points matériels M_i, ce qui permet d'écrire 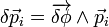$\delta\vec{p}_i=\overrightarrow{\delta\phi}\wedge\vec{p}_i$ . Dès lors les équations canoniques de Hamilton se mettent sous la forme vectorielle:

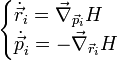\begin{cases} \dot{\vec{r}}_i=\vec{\nabla}_{\vec{p}_i}H \\ \dot{\vec{p}}_i=-\vec{\nabla}_{\vec{r}_i}H \end{cases}

La variation correspondante du hamiltonien H résultant de la rotation élémentaire de vecteur 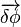$\overrightarrow{\delta\phi}$ peut s'exprimer par :

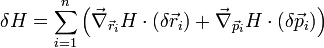\delta H= \sum_{i=1}^{n} \left(\vec{\nabla}_{\vec{r}_i}H\cdot(\delta\vec{r}_i)+\vec{\nabla}_{\vec{p}_i}H\cdot(\delta\vec{p}_i)\right)

soit en tenant compte des équations de Hamilton :

\delta H= \sum_{i=1}^{n} \left(-\dot{\vec{p}}_i\cdot(\overrightarrow{\delta\phi}\wedge\vec{r}_i)+\dot{\vec{r}}_i\cdot(\overrightarrow{\delta\phi}\wedge\vec{p}_i)\right)=-\overrightarrow{\delta\phi}\cdot\left[\sum_{i=1}^{n}\left(\vec{r}_i\wedge\dot{\vec{p}}_i+\dot{\vec{r}}_i\wedge\vec{p}_i\right)\right]

qui se met aussitôt sous la forme:

\delta H = -\overrightarrow{\delta\phi}\cdot\left[\frac{d}{dt}\left(\sum_{i=1}^{n} \vec{r}_i\wedge\vec{p}_i\right)\right]

Puisque ce résultat est valable pour toute rotation élémentaire arbitraire, l'isotropie de l'espace pour un système isolé implique alors que la quantité 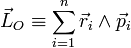$\vec{L}_O \equiv\sum_{i=1}^{n} \vec{r}_i\wedge\vec{p}_i$ , appelé moment cinétique du système par rapport à l'origine O, soit une constante du mouvement. Il est clair que pour un seul point matériel, 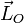$\vec{L}_O$ est bien identique à la définition donnée plus haut.

Par ailleurs en procédant toujours en coordonnées cartésiennes, et compte tenu du fait que 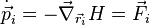$\dot{\vec{p}}_i=-\vec{\nabla}_{\vec{r}_i}H=\vec{F}_i$ , résultante des forces appliquées au point matériel M_i, il est possible de déduire le théorème du moment cinétique :

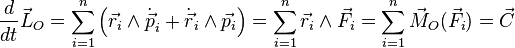\frac{d}{dt}\vec{L}_O=\sum_{i=1}^{n}\left(\vec{r}_i\wedge\dot{\vec{p}}_i+\dot{\vec{r}}_i\wedge\vec{p}_i\right)=\sum_{i=1}^{n} \vec{r}_i\wedge\vec{F}_i=\sum_{i=1}^{n} \vec{M}_O(\vec{F}_i)=\vec{C}

\vec{C}

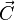étant la résultante du moment des forces en O.

La conservation du moment cinétique par rapport à un point O est donc directement lié à l'invariance par rotation du hamiltonien (ou du Lagrangien) du système: c'est en particulier le cas pour un système non isolé mais soumis à un champ extérieur possédant une invariance par rotation autour de O. Ce type de champ très important en physique est un champ à force centrale, de centre de force O : son mouvement est alors caractérisé par la conservation du moment cinétique du système par rapport à O.

De même, l'invariance par rotation autour d'un axe donné du hamiltonien du système (symétrie axiale) impliquera la conservation de la composante du moment cinétique du système par rapport à cet axe, puisque alors 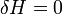$\delta H=0$ pour toute rotation élémentaire autour de cet axe. Le moment résultant 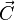$\vec{C}$ des forces appliquée en O, donc la dérivée du moment cinétique en ce même point, est, elle, directement liée à la variation du hamiltonien dans une rotation élémentaire du système d'un angle δϕ autour de O.

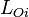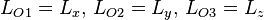Enfin, il est possible en utilisant les crochets de Poisson de montrer la relation suivante entre les composantes cartésiennes $L_{Oi}$ du moment cinétique, en posant $L_{O1}=L_x,\,L_{O2}=L_y,\,L_{O3}=L_z$ :

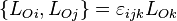\{L_{Oi},L_{Oj}\}=\varepsilon_{ijk} L_{Ok}

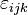\varepsilon_{ijk}

étant le symbole de Levi-Civita.

Cette relation à une forme très proche de celle de la relation de commutation des opérateurs de moment cinétique en mécanique quantique :

\left[\hat L_i,\hat L_j\right]=i\hbar\varepsilon_{ijk}\hat L_k.

Moment cinétique et mouvement à force centrale

Article détaillé : mouvement à force centrale.

Cas général

Notion de force centrale

Démonstration du moment angulaire

Un cas particulier très important d'utilisation du moment cinétique est celui du mouvement à force centrale, pour lequel le moment cinétique est conservé.

La notion de force centrale est définie de diverses façons suivant les auteurs:

- soit comme une force 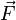$\vec{F}$ dont la direction passe par un point fixe dans (R), appelé centre de force, donc en posant 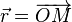$\vec{r}=\overrightarrow{OM}$ telle que 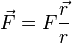$\vec{F}=F\frac{\vec{r}}{r}$ à tout instant, F étant quelconque : il s'agit donc d'une définition purement géométrique;

- soit comme une force dont non seulement la direction passe à tout instant par un point fixe O, mais qui dérive d'un potentiel 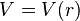$V = V(r)$ ne dépendant que de la distance au centre de force : il s'agit donc d'une force également conservative.

Si en pratique les cas de mouvement à force centrale se limite le plus souvent à des forces conservatives (gravitation par exemple), il est utile de distinguer les deux notions de force centrale et de force conservative. Aussi une force sera considérée comme centrale si à tout instant sa direction passe par un point fixe O, qu'elle soit ou non conservative.

Ceci permet de distinguer dans les conséquences du caractère "central" de la force ce qui est lié à l'aspect géométrique (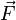 $\vec{F}$ est toujours colinéraire à 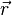$\vec{r}$ ) de ce qui est lié à un éventuel caractère conservatif, donc le fait que l'énergie mécanique du point matériel est conservée.

Ainsi si toute force dérivant d'un potentiel scalaire dépendant uniquement de la distance r à l'origine est centrale, une force non conservative a priori comme la tension du fil d'un pendule simple, qui pointe à tout instant vers le point de fixation du pendule, sera également considérée comme une force centrale avec cette définition^[5]

Conservation du moment cinétique et planéité de la trajectoire

Le mouvement d'un point matériel M sous le seul effet d'une force centrale est un exemple de mouvement pour lequel le moment cinétique par rapport au centre de force est conservé^[6]. En effet, en prenant pour origine le centre de force O, le théorème du moment cinétique donne :

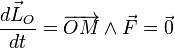\frac{\vec{dL_{O}}}{dt}=\overrightarrow{OM}\wedge\vec{F} = \vec{0}

, puisque

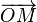\overrightarrow{OM}

\vec{F}

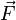sont à tout instant colinéaires si la force est centrale.

Par suite le moment cinétique 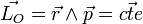$\vec{L_{O}}=\vec{r}\wedge \vec{p}=\vec{cte}$ est une intégrale première du mouvement, et donc le vecteur position 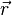$\vec{r}$ et la quantité de mouvement 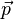$\vec{p}$ du corps sont à tout instant perpendiculaires à un vecteur de direction constante : la trajectoire est donc plane, entièrement contenue dans le plan perpendiculaire à 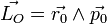$\vec{L_{O}}=\vec{r_{0}}\wedge \vec{p_{0}}$ (l'indice "0" désigne les valeurs initiales des grandeurs).

Le mouvement ne comportant que deux degrés de liberté, il est possible de se placer en coordonnées polaires (r,θ) dans le plan de la trajectoire. Il vient ainsi 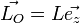$\vec{L_{O}}=L\vec{e_{z}}$ , avec 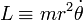$L\equiv mr^{2}\dot{\theta}$ constante.

Loi des aires et formule de Binet

La conservation du moment cinétique par rapport au centre de force O peut s'interpréter physiquement par le fait que non seulement la trajectoire est plane mais également que le vecteur position du point matériel "balaie des aires égales en des temps égaux", autrement dit que le mouvement vérifie la loi des aires, mis en évidence par Kepler en 1609 dans le cas du mouvement des planètes (cf. loi de Kepler)^[7].

En effet en posant 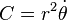$C = r^2\dot{\theta}$ (= constante), l'aire élémentaire 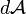$d\mathcal{A}$ balayée par 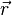$\vec{r}$ pendant la durée dt s'écrit 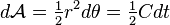$d\mathcal{A}= \tfrac{1}{2}r^2d\theta = \tfrac{1}{2}Cdt$ . Par suite le taux de variation de cette aire balayée, appelé vitesse aérolaire 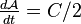$\tfrac{d\mathcal{A}}{dt} = C/2$ est bien une constante, la quantité C est souvent appelée pour cette raison constante des aires.

Par ailleurs, le fait que 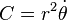$C = r^2\dot{\theta}$ soit une constante du mouvement permet d'exprimer 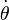$\dot{\theta}$ sous la forme 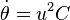$\dot{\theta}=u^2C$ avec u=1/r. On peut alors éliminer 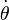$\dot{\theta}$ dans les formules cinématiques donnant la vitesse et l'accélération du point matériel en coordonnées polaires, ce qui conduit à établir les deux formules de Binet. En particulier il est possible de démontrer que l'accélération du point matériel se met alors sous la forme:

\vec{a}_M=-u^2C^2\left[\frac{d^2u}{d\theta^2}+u\right]\vec{e}_r

, (2ème de formule de Binet).

Bien entendu, cette formule montre bien que l'accélération est dirigée vers le centre de force, puisque la force l'est, comme le prévoit la relation fondamentale de la dynamique. Il est utile de souligner que la loi des aires comme les formules de Binet sont des conséquences du seul caractère central de la force, et n'implique pas que celle-ci soit conservative.

Séparation radiale-angulaire de l'énergie cinétique et barrière centrifuge

Compte tenu du fait que 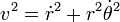$v^{2}=\dot{r}^{2}+r^{2}\dot{\theta}^{2}$ en coordonnées polaires, l'énergie cinétique du point matériel peut dans le cas d'un mouvement à force centrale se séparer en une partie dite radiale et une partie dite angulaire. En effet il vient aussitôt:

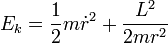E_{k}=\frac{1}{2}m\dot{r}^{2}+\frac{L^{2}}{2mr^{2}}

le premier terme est identique à celui qu'aurait l'énergie cinétique du point matériel s'il se déplaçait à vitesse 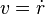$v=\dot{r}$ le long de la direction 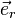$\vec{e}_r$ , et donc est correspond à l’énergie cinétique radiale. Le second terme, dit angulaire de par son lien avec le mouvement orthoradial, correspond plutôt à une énergie potentielle "répulsive" en 1/r^2, dans la mesure où L est constant, pour un point matériel considéré comme en mouvement unidimensionnel selon la direction radiale. Ce terme est souvent appelé barrière centrifuge.

Si là encore la séparation radiale-angulaire de l'énergie cinétique est uniquement la conséquence du caractère central de la force et ne nécessite nullement que celle-ci soit conservative, elle a une importance particulière dans ce dernier cas, car il est alors possible de se ramener à un mouvement unidimensionnel.

Cas où la force centrale dérive d'une énergie potentielle

Article détaillé : problème à deux corps.

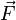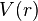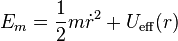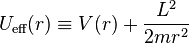Si la force centrale $\vec{F}$ dérive d'une énergie potentielle $V(r)$ , l'énergie mécanique du corps se met sous la forme: $E_{m} = \frac{1}{2}m\dot{r}^{2} + U_{\text{eff}}(r)$ avec $U_{\text{eff}}(r)\equiv V(r) + \frac{L^{2}}{2mr^{2}}$ , énergie potentielle effective.

Le problème se réduit alors à un mouvement unidimensionnel d'une particule fictive dans un potentiel 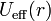$U_{\text{eff}}(r)$ . Le terme 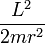$\frac{L^{2}}{2mr^{2}}$ étant positif et croissant à courte distance, il joue le rôle de "barrière de potentiel centrifuge". La nature des mouvements possibles dépend alors du potentiel V(r) ainsi que de l'énergie mécanique totale du point matériel.

En général les trajectoires obtenues pour une énergie potentielle V(r) quelconque ne sont pas des courbes fermées : seuls le potentiel coulombien attractif 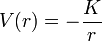$V(r)=-\frac{K}{r}$ (K constante) et le potentiel harmonique 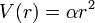$V(r)=\alpha r^{2}$ en donneront (Théorème de Bertrand)^[8] (cf. problème à deux corps).

Cas d'un système matériel

Moment cinétique

La notion de moment cinétique se généralise sans difficulté par additivité à un système matériel, c'est-à-dire à un corps que l'on ne peut pas assimiler à un simple point géométrique. Le moment angulaire total est obtenu en additionnant ou intégrant le moment angulaire de chacun de ses constituants. Il est également possible de se placer dans la limite des milieux continus pour décrire certains systèmes mécaniques (solides, notamment).

Suivant que l'on adopte un modèle discret ou continu, le moment cinétique du système (S) par rapport à un point O s'écrit :

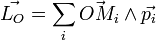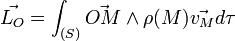
$\vec{L_{O}}=\sum_{i} \vec{OM_{i}}\wedge \vec{p_{i}}$ ou $\vec{L_{O}}=\int_{(S)} \vec{OM}\wedge \rho (M)\vec{v_{M}}d\tau$

Ces expressions générales ne sont guère utilisables directement. Le théorème de Koenig relatif au moment cinétique permet d'en donner une forme plus compréhensible physiquement.

Théorème de Koenig pour le moment cinétique

Article détaillé : Théorèmes de König (mécanique).

Soit G le centre d'inertie du système, M la masse totale du système, alors il est possible de montrer que pour tout système matériel:

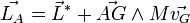\vec{L_{A}}=\vec{L}^* + \vec{AG}\wedge M\vec{v_{G}}

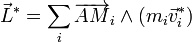$\vec{L}^*=\sum_{i} \overrightarrow{AM}_i \wedge (m_i \vec{v}_i^*)$ étant le moment cinétique propre du système, c'est-à-dire celui évalué dans le référentiel barycentrique (R^*) associé à (R), qui est le référentiel lié à G dont les axes sont en translation par rapport à ceux de (R). 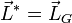Il est possible de montrer d'après les propriétés du centre d'inertie G qu'en fait le moment cinétique propre ne dépend pas du point A où il est évalué, et est tel que $\vec{L}^*=\vec{L}_G$ .

Le moment cinétique d'un système fermé en un point est donc égal au moment cinétique du centre d'inertie G affecté de la masse totale en ce point, augmenté du moment cinétique propre du système. Il est donc possible de séparer le mouvement du centre d'inertie du mouvement propre du système.

La séparation des deux types de moment cinétique par le théorème est assez intuitive : ainsi pour la Terre, dans le référentiel héliocentrique, il est a priori évident que l'on a un moment cinétique "orbital" lié à son mouvement de révolution autour du Soleil, et un moment cinétique "propre", lié à sa rotation propre autour de l'axe des pôles.

Cas d'un solide : tenseur d'inertie

Pour un solide (S), la vitesse de tout point M_i est donnée dans le référentiel barycentrique (R^*) par le champ des vitesses 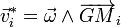$\vec{v}_i^*=\vec{\omega}\wedge\overrightarrow{GM}_i$ ,
avec 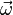$\vec{\omega}$ vecteur rotation propre du solide (S) par rapport à (R^*) ou (R), puisque (R^*) est en translation relativement à (R). De façon simple, ce vecteur traduit la rotation d'un système de coordonnées rigidement lié au solide par rapport à (R^*) ou (R).

Il vient dès lors l'expression suivante pour le moment cinétique propre 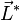$\vec{L}^*$ du solide (S):

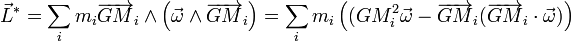\vec{L}^*=\sum_{i} m_i \overrightarrow{GM}_i\wedge\left(\vec{\omega}\wedge\overrightarrow{GM}_i\right)=\sum_{i} m_i\left((GM_i^2\vec{\omega}-\overrightarrow{GM}_i(\overrightarrow{GM}_i\cdot\vec{\omega})\right)

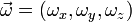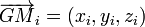en posant en coordonnées cartésiennes $\vec{\omega}=(\omega_x,\omega_y,\omega_z)$ et $\overrightarrow{GM}_i=(x_i,y_i,z_i)$ , il vient pour les différentes composantes de $\vec{L}^*$ :

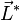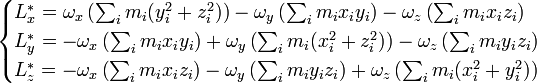\begin{cases} L_x^*=\omega_x\left(\sum_{i} m_i(y_i^2+z_i^2)\right)-\omega_y\left(\sum_{i} m_i x_i y_i\right)-\omega_z\left(\sum_{i} m_i x_i z_i\right) \\ L_y^*=-\omega_x\left(\sum_{i} m_i x_i y_i\right)+\omega_y\left(\sum_{i} m_i(x_i^2+z_i^2)\right)-\omega_z\left(\sum_{i} m_i y_i z_i\right) \\ L_z^*=-\omega_x\left(\sum_{i} m_i x_i z_i\right)-\omega_y\left(\sum_{i} m_i y_i z_i\right)+\omega_z\left(\sum_{i} m_i(x_i^2+y_i^2)\right) \end{cases}

qui peut aussi s'écrire sous la forme intrinsèque $\vec{L}^*=\bar{\bar{I}}\vec{\omega}$ ,
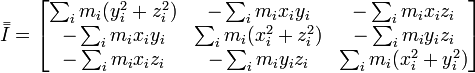avec $\bar{\bar{I}}=\begin{bmatrix}\sum_{i} m_i(y_i^2+z_i^2) & -\sum_{i} m_i x_i y_i & - \sum_{i} m_i x_i z_i \\ -\sum_{i} m_i x_i y_i & \sum_{i} m_i(x_i^2+z_i^2) &-\sum_{i} m_i y_i z_i\\ -\sum_{i} m_i x_i z_i & -\sum_{i} m_i y_i z_i & \sum_{i} m_i(x_i^2+y_i^2) \end{bmatrix}$ , tenseur d'inertie du solide (S).

Il en résulte qu'en général le moment cinétique propre du solide 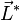$\vec{L}^*$ n'est pas colinéaire à son vecteur rotation 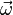$\vec{\omega}$ dans (R).

Le tenseur d'inertie est une caractéristique propre du solide (S), et donne la répartition des masses en son sein. Il s'agit d'un tenseur symétrique. Ses éléments diagonaux sont constitués des moments d'inertie du solide par rapport aux axes (Ox), (Oy) et (Oz) respectivement, et ses éléments non diagonaux sont égaux à l'opposé des moments d'inertie par rapport aux plans (xOy), (xOz) et (yOz).

Du fait de son caractère symétrique, il est toujours possible de diagonaliser ce tenseur par un choix judicieux des axes, qui sont appelés alors axes principaux d'inertie.

Moment cinétique relativiste

La notion de moment cinétique peut être définie dans le cadre de la théorie de la relativité restreinte, sous la forme d'un tenseur antisymétrique^[9].

Dans le domaine relativiste, il n'est pas possible de considérer les coordonnées d'espace indépendamment du temps, et aux vecteurs position 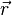$\vec{r}$ et quantité de mouvement 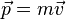$\vec{p}=m\vec{v}$ de la mécanique newtonienne, correspondent deux quadrivecteurs:

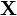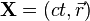le quadrivecteur position-temps, noté $\mathbf{X}$ , avec $\mathbf{X}=(ct,\vec{r})$ ;
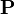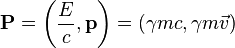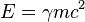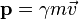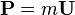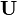le quadrivecteur impulsion-énergie, noté $\mathbf{P}$ , avec $\mathbf{P} = \left(\frac{E}{c},\mathbf{p}\right) = (\gamma mc,\gamma m\vec{v})$ , où $E=\gamma m c^2$ et $\mathbf{p}=\gamma m\vec{v}$ correspondent respectivement à l'énergie et la quantité de mouvement relativistes de la particule. Le quadrivecteur impulsion-énergie est en fait donné par $\mathbf{P}=m\mathbf{U}$ où $\mathbf{U}$ est le quadrivecteur vitesse, défini par 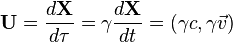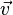$\mathbf{U}=\frac{d\mathbf{X}}{d\tau}=\gamma \frac{d\mathbf{X}}{dt}=(\gamma c,\gamma \vec{v})$ , $\vec{v}$ étant le vecteur vitesse "ordinaire" de la particule, et 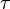$\tau$ le temps propre.

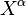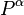Les composantes de ces deux quadrivecteurs étant notées $X^\alpha$ et $P^\alpha$ avec α = 0,1,2,3, il est possible de définir un (quadri)tenseur contravariant antisymétrique du second ordre 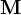$\mathbf{M}$ appelé (quadri)tenseur moment cinétique dont les composantes sont données par:

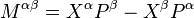M^{\alpha\beta}=X^\alpha P^\beta - X^\beta P^\alpha

du fait de son caractère antisymétrique, ce tenseur ne possède en réalité que 6 composantes indépendantes, trois mixtes (M⁰¹, M⁰² et M⁰³) et trois autres du genre espace (M¹², M²³ et M¹³). En explicitant ces dernières, il vient aussitôt:

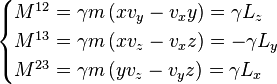\begin{cases} M^{12} = \gamma m\left(xv_y-v_x y\right)=\gamma L_z \\ M^{13} = \gamma m\left(xv_z-v_x z\right)=-\gamma L_y \\ M^{23} = \gamma m\left(yv_z-v_y z\right)=\gamma L_x \end{cases}

où 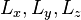$L_x,L_y,L_z$ représentent les composantes cartésiennes du moment cinétique non relativiste. Dans la limite des faibles vitesses devant c, γ → 1 et les trois composantes spatiales indépendantes du tenseur coïncident, au signe près, à celle du moment cinétique "ordinaire".

Notes et références

Notes

↑ La notation 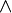$\wedge$ est celle du produit vectoriel.
↑ Par rapport à un point O mobile dans (R), le théorème du moment cinétique s'écrit: 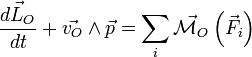$\frac{\vec{dL_{O}}}{dt}+\vec{v_{O}}\wedge \vec{p}=\sum_{i} \vec{\mathcal{M}_{O}}\left (\vec{F_{i}}\right)$ , la seule différence vient de l'addition d'un terme complémentaire 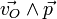$\vec{v_{O}}\wedge \vec{p}$ dans le membre de gauche de la relation précédente.
↑ De façon plus rigoureuse, il faut considérer un axe (Δ₀) passant par O et perpendiculaire au plan formé par 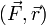$(\vec{F},\vec{r})$ , de vecteur unitaire 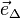$\vec{e}_\Delta$ . 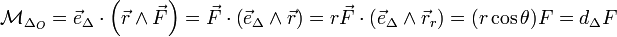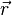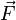Le moment par rapport à l'axe (Δ₀) est alors donné par $\mathcal{M}_{\Delta_O} = \vec{e}_{\Delta}\cdot\left(\vec{r}\wedge\vec{F}\right)=\vec{F}\cdot\left(\vec{e}_{\Delta}\wedge\vec{r}\right)=r\vec{F}\cdot\left(\vec{e}_{\Delta}\wedge\vec{r}_r\right)=(r\cos{\theta})F=d_\Delta F$ , avec θ angle entre $\vec{r}$ et $\vec{F}$ , d_Δ étant la distance entre l'axe (Δ₀) et la droite support de 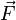$\vec{F}$ (ou bras de levier). Cette quantité traduit bien l'effet de 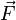$\vec{F}$ en ce qui concerne la rotation de M autour de l'axe (Δ₀).
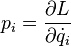↑ La démonstration se fait de la même façon en formalisme Lagrangien, en tenant compte du fait que par définition $p_i=\frac{\partial L}{\partial \dot{q_i}}$ .
↑ Dans cette situation cependant s'ajoute le poids de la masselotte attachée au fils, qui est une force non-centrale
↑ Cependant l'exemple le plus important (et "historique") de mouvement à force centrale est le problème à deux corps, pour lequel on considère deux points matériels en interaction gravitationnelle. Comme il est indiqué dans l'article qui y est consacré, il se ramène en fait à un problème à un seul corps (particule fictive) soumis à une force centrale, aussi la situation envisagée ici à un intérêt.
↑ Kepler a mis en évidence cette propriété par le calcul, sans pouvoir l'expliquer. C'est Newton en 1687 qui expliquera l'origine de cette "loi".
↑ Cela provient de l'existence, pour ces potentiels, d'une intégrale première additionnelle (pour le potentiel coulombien, il s'agit du vecteur de Runge-Lenz), associé à une symétrie supplémentaire (par transformation du groupe O(4)).
↑ Pour cette partie, cf. Herbert Goldstein, Charles P. Poole Jr., John L. Safko, Classical mechanics [détail des éditions] et Lev Landau et Evguéni Lifchitz, Physique théorique, tome 2 : Théorie des champs [détail des éditions], chapitre 2.

Voir aussi

Bibliographie

Lev Landau et Evguéni Lifchitz, Physique théorique, tome 1 : Mécanique [détail des éditions]
Herbert Goldstein, Charles P. Poole Jr., John L. Safko, Classical mechanics [détail des éditions]
Perez, Cours de physique : mécanique - 6^e édition, Masson, Paris, 2001.

Liens externes

Vidéos d'illustration:
- (fr) Une vidéo explicative sur la conservation du moment cinétique
- (fr) Une autre vidéo illustrant la conservation du moment cinétique
- (fr) Liens vers diverses vidéos illustrant la notion de moment cinétique et sa conservation

Portail de la physique

This article is issued from Wikipédia - version of the Tuesday, July 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Moment cinétique (mécanique classique)

Cas d'un point matériel

Définition

Théorème du moment cinétique pour un point matériel

Exemples d'application

Moment cinétique et isotropie

Moment cinétique et mouvement à force centrale

Cas général

Notion de force centrale

Conservation du moment cinétique et planéité de la trajectoire

Loi des aires et formule de Binet

Séparation radiale-angulaire de l'énergie cinétique et barrière centrifuge

Cas où la force centrale dérive d'une énergie potentielle

Cas d'un système matériel

Moment cinétique

Théorème de Koenig pour le moment cinétique

Cas d'un solide : tenseur d'inertie

Moment cinétique relativiste

Notes et références

Notes

Voir aussi

Articles connexes

Bibliographie

Liens externes

Medical Encyclopedia