Symétrie
Un système est symétrique quand on peut permuter ses éléments en laissant sa forme inchangée. Le concept d'automorphisme permet de préciser cette définition.
Un papillon, par exemple, est symétrique parce qu'on peut permuter tous les points de la moitié gauche de son corps avec tous les points de la moitié droite sans que son apparence soit modifiée. On peut échanger les deux moitiés sans changer la forme de l'ensemble. Les figures symétriques rendent visible l'égalité des formes parce que les parties permutables ont toujours la même forme. On pourrait en faire une définition du concept : une figure est symétrique lorsqu'elle répète une même forme de façon régulière.





Qu'est-ce qu'une forme ?
Le concept de forme est défini en mathématiques à partir de celui d'isomorphisme. Deux systèmes isomorphes ont la même forme.
Un système, une structure mathématique, un modèle, un univers, ou un monde, au sens mathématique, est déterminé avec plusieurs ensembles :
- l’ensemble U des éléments du système, ses points, ses atomes ou ses constituants élémentaires,
- l’ensemble des prédicats fondamentaux, propriétés de base des éléments et relations entre eux,
- l’ensemble des opérateurs, ou fonctions, qui déterminent davantage la structure du système.
Souvent par abus de langage, on identifie une structure par l'ensemble U de ses éléments.
Soient U et U' deux structures définies par les relations binaires R et R' respectivement. Une transformation inversible t (une bijection) de U dans U' est un isomorphisme pour R et R' lorsque :
pour tout x et tout y dans U, x R y si et seulement si tx R' ty
S'il existe une telle transformation t, U et U' sont isomorphes - plus précisément les structures (U,R) et (U',R') sont isomorphes.
Cette définition peut être aisément généralisée à toutes les relations, quel que soit le nombre de leurs arguments, et aux prédicats monadiques.
Soient U et U' deux structures définies par les opérateurs binaires + et +' respectivement. Une bijection t de U dans U' est un isomorphisme pour + et +' lorsque :
pour tout x et tout y dans U, t(x+y) = tx +' ty
S'il existe une telle transformation t, U et U' sont isomorphes - plus précisément les structures (U,+) et (U',+') sont isomorphes.
Cette définition peut être aisément généralisée à tous les opérateurs, quel que soit le nombre de leurs arguments.
À un opérateur binaire +, on peut associer une relation ternaire définie par x+y=z. On voit alors que la définition d’un isomorphisme pour un opérateur est un cas particulier de la définition d’un isomorphisme pour les relations.
Lorsque les structures sont définies avec plusieurs prédicats, monadiques ou relationnels, et plusieurs opérateurs, les isomorphismes sont les bijections qui sont des isomorphismes pour tous les prédicats et tous les opérateurs. Ainsi défini le concept d'isomorphisme est universel, il peut être appliqué à toutes les structures mathématiques (les définitions d'un homéomorphisme et d'un difféomorphisme requièrent davantage de précisions.)
Les groupes d'automorphismes
Le concept d'automorphisme permet de préciser celui de symétrie. Les permutations, ou transformations, qui laissent la forme inchangée, sont les symétries, ou les automorphismes, du système. Un automorphisme est un isomorphisme interne. Les automorphismes d'une structure U sont les bijections de U dans U qui sont des isomorphismes pour tous les prédicats et tous les opérateurs qui déterminent la structure. Plus explicitement :
Une fonction inversible, ou bijection, de U dans U est un automorphisme pour une relation binaire R lorsque
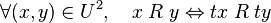
Cette définition d’un automorphisme se généralise aisément aux prédicats monadiques et à toutes les relations, quel que soit le nombre de leurs arguments. Pour un prédicat monadique P, une transformation t est un automorphisme lorsque
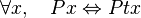
Dans l’exemple du papillon, la symétrie entre la gauche et la droite est un automorphisme pour les propriétés (les prédicats monadiques) de couleur. Un point a la même couleur que son point symétrique.
Une transformation t est un automorphisme pour un opérateur binaire + lorsque
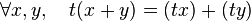
Cette définition d’un automorphisme se généralise aisément à tous les opérateurs, quel que soit le nombre de leurs arguments. t est un automorphisme pour un opérateur à un argument lorsque
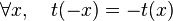
Autrement dit, une transformation est un automorphisme pour un opérateur monadique (une fonction d'une seule variable) lorsqu'elle commute avec lui. Lorsque des opérateurs commutent entre eux, ils sont tous des automorphismes les uns vis-à-vis des autres, au sens où toute forme définie par l'un est conservée par tous les autres.
Les automorphismes d'une structure forment un groupe, au sens de l'algèbre, son groupe de symétries. Pour tous automorphismes t et u, t°u est un automorphisme et l’inverse de t est un automorphisme. La transformation identique (qui associe toujours x à x) est un automorphisme. Autrement dit :
- Si une forme est conservée par deux transformations effectuées séparément, elle est aussi conservée lorsqu'on effectue les deux transformations l'une à la suite de l'autre. C'est simplement la transitivité de l'égalité des formes.
- Si une forme est conservée par une transformation, elle est aussi conservée par la transformation inverse.
- En outre, il existe toujours une transformation identique, qui ne transforme rien, qui est donc toujours un automorphisme, puisqu'elle ne peut pas modifier quoi que ce soit.
Ces trois propriétés font de l'ensemble des automorphismes d'un système un groupe pour sa loi de composition interne naturelle.
Exemples
Les isométries
Les isométries sont les automorphismes de la structure d'espace métrique ou, dit autrement, de l'espace pour sa structure métrique. t est une isométrie si et seulement si d(x,y)=d(tx,ty) pour tous x et y, où d(x,y) est la distance entre x et y. Ce sont des automorphismes pour toutes les relations binaires d(x,y)=L où L est un nombre réel positif, parce que d(x,y)=L si et seulement si d(tx,ty)=L.
L’espace euclidien en son entier est un des systèmes les plus symétriques, au sens où l’ensemble des façons de permuter simultanément tous ses points sans modifier sa structure, son groupe de symétries, est l’un des moins contraints, parmi les groupes des symétries géométriques. Tous les points de l’espace sont semblables. Ils n’ont pas d’autre qualité que d’être un point et ils ont tous les mêmes relations avec le reste de l’espace. Que n’importe quel point peut être transformé en n’importe quel autre par une isométrie traduit cette égalité de tous les points de l'espace.
Si l’on brise la symétrie de l’espace en introduisant une sphère, alors tous les points ne sont plus semblables : il y a des points sur la sphère, d’autres à l’intérieur et d’autres à l’extérieur. En revanche, tous les points de la sphère sont semblables. N’importe lequel d’entre eux peut être transformé en n’importe quel autre par une isométrie : une rotation autour du centre de la sphère. Comme les chevaliers de la Table Ronde, aucun n'a une position privilégiée. Ils sont tous également placés les uns par rapport aux autres.
Les symétries des molécules et des cristaux
La structure d'une molécule ou d'un cristal est définie en mécanique quantique par la fonction d'onde de tous ses constituants, noyaux et électrons. Mais pour de nombreux usages, on peut modéliser la structure simplement par les positions des centres des atomes ou des ions. Avec un tel modèle, la structure est complètement décrite avec les prédicats monadiques "est le centre d'un atome de l'espèce i" et "est le centre d'un ion de l'espèce j". Les symétries de la molécule ou du cristal peuvent être alors définies comme les isométries de l'espace qui sont aussi des automorphismes pour les prédicats monadiques de structure. Les symétries transforment toujours le centre d'un atome ou d'un ion en un centre d'un atome ou d'un ion de même espèce.





Les similitudes
Selon l'usage courant une structure et un modèle réduit ont la même forme. Pour préciser ce concept de forme, il faut définir les automorphismes de l'espace comme des similitudes. Elles conservent les rapports de distance, elles sont donc des automorphismes pour les prédicats quaternaires d(A,B)=k.d(C,D), pour tous les nombres réels positifs k. Plus explicitement, lorsque s est une similitude :
d(A,B)=k.d(C,D) si et seulement si d(sA,sB)=k.d(sC,sD)
pour tous les points A,B,C et D et tout nombre réel positif k.
La spirale logarithmique
Une spirale logarithmique est définie avec l'équation
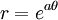
où  et
et 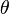 sont les coordonnées polaires d'un point P.
sont les coordonnées polaires d'un point P.
Cette équation détermine le prédicat monadique "est sur la spirale" :
 si et seulement si P est sur la spirale.
si et seulement si P est sur la spirale.
Une telle spirale est invariante pour toutes les transformations composées d'une rotation d'angle  et d'une homothétie de rapport
et d'une homothétie de rapport 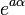 . Ces similitudes d'angle
. Ces similitudes d'angle 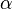 et de rapport
et de rapport 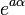 sont donc les symétries de la spirale.
sont donc les symétries de la spirale.
Les mouvements périodiques

Les trajectoires périodiques (les oscillations, les vibrations, les mouvements des satellites,...) sont des structures spatio-temporelles symétriques pour certaines translations dans le temps. T est une période d'une trajectoire lorsque (x,t) est sur la trajectoire si et seulement si (x,t+T) l'est aussi. Les translations de durée T, 2T, 3T,... , considérées comme des transformations de l'espace-temps sont des automorphismes pour le prédicat monadique "est sur la trajectoire".
Les symétries de l'espace-temps
La structure de l'espace-temps peut être définie par la pseudo-métrique de Minkowski : à deux points quelconques  et
et 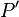 de coordonnées
de coordonnées 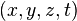 et
et 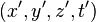 respectivement, on associe un nombre réel, positif ou négatif (le carré de sa distance relativiste):
respectivement, on associe un nombre réel, positif ou négatif (le carré de sa distance relativiste):
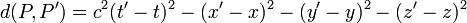
où  est la vitesse de la lumière.
est la vitesse de la lumière.
Une transformation  est une symétrie si et seulement si pour tous
est une symétrie si et seulement si pour tous  et
et 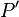 :
:
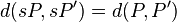
Autrement dit, 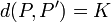 si et seulement si
si et seulement si 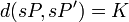 , pour toute constante réelle
, pour toute constante réelle 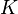 .
.
Les symétries de l'espace-temps sont les automorphismes pour tous les prédicats binaires 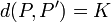 , où
, où 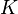 est n'importe quel nombre réel.
est n'importe quel nombre réel.
Les symétries de l'espace-temps forment le groupe de Poincaré.
Les symétries de l'espace et du temps ont une importance fondamentale pour la physique à cause du principe de l'égalité de tous les observateurs. Comme autour d'une table ronde nous sommes tous également placés les uns par rapport aux autres. Aucun d'entre nous n'a une position privilégiée. Toute observation faite par l'un peut être faite par un autre. On peut donc permuter les observateurs sans modifier les observations. Puisqu'à chaque observateur est lié un référentiel, les symétries de l'espace-temps doivent permettre de transformer n'importe quel référentiel en n'importe quel autre. Le groupe des symétries de l'espace-temps est donc une expression mathématique du principe de l'égalité de tous les observateurs.
Bibliographie
- Amaury Mouchet, L'élégante efficacité des symétries, Dunod, 2013 (ISBN 9782100589371) 240 pages
- Henri Bacry, La symétrie dans tous ses états, Vuibert, 2000 (ISBN 9782711752676) 447 pages
- Claude Cohen-Tannoudji, Yves Sacquin, Symétrie et brisure de symétrie, EDP Sciences, 1999 (ISBN 9782868833990)
- Jean Sivardière, Description de la symétrie (ISBN 9782868837219) et Symétrie et propriétés physiques (ISBN 9782868837226), EDP Sciences, 2004
- Bas van Fraassen, Lois et symétrie, Vrin, 1994 (ISBN 9782711612185) 520 pages
- Hermann Weyl, Symétrie et mathématique moderne, Champs|Flammarion, 1964 (ISBN 2080813668) 153 pages
- Cécile Malgrange, Christian Ricolleau et François Lefaucheux, Symétrie et propriétés physiques des cristaux, éd. EDP Sciences, 2011 (ISBN 9782759804993) 496 pages
- Sidney Kettle, Christine Assfeld, Xavier Assfeld, Symétrie et structure, théorie des groupes en chimie, Masson, 1997 (ISBN 9782225855269) 379 pages
Voir aussi
- En Botanique : Symétrie florale
- En Chimie : symétrie moléculaire, chiralité, isomérie
- En Physique : symétrie (physique)
- En Géométrie : symétrie (transformation géométrique)
- Asymétrie
- Dissymétrie
- Théorie des groupes
- Fractales
- Brisure de symétrie
- Principe de Curie
- Portail de la géométrie